薄膜及晶硅电池组件功率推算研究

郝国强 李红波 徐清国 叶晓军 柳 翠 袁 晓

1.华东理工大学材料科学与工程学院

2.上海太阳能工程技术研究中心有限公司

0 引言

光伏发电具有非常显著的能源利用、环境保护和经济发展效益，是最优质的清洁能源之一[1]。而分布式光伏发电是利用太阳能的一种有效方式，是可再生能源体系的重要组成部分，正在引领新一轮的能源革命[2]。薄膜及晶硅电池是目前应用较广的光伏发电应用形式，然而，目前对于薄膜及晶硅光伏系统的评价机制不健全，尚未形成完整可行的评价方案。当前业内普遍采用的是IEC 61724-2014[3]修订版中“性能比PR”的理论进行光伏系统的评价。

通过对该标准中理论算法的研究，分析得到薄膜及晶硅光伏系统的评价需建立在其比较准确的理论发电量测试方法基础上。根据太阳电池发电原理[4]，前人总结了目前普遍适用的一种光伏组件的功率推算算法[5,6]，该算法需要大量的实验去确定光伏组件的相对温度系数，而且该系数事实上也很难精确计算，不可避免地会引入一些人为因素进而引入二次误差[7,8]，该测试方案很难满足其高精度的测试结构要求。此外，在光伏系统现场，现有的手持式光伏组件及阵列功率测试仪的精确度不高，很难克服光谱失配、温度以及辐照度变化的影响并保持一定的准确性[9]。

本文通过对现有的几种组件功率推算算法的研究，充分利用外推法和内插法等数据分析理论，引入高精确度的光伏组件功率推算理论[10]。该理论可以对光伏发电系统现场的实时功率以及装机容量的推算发挥重要作用，利于光伏系统评价工作的开展。

1 功率推算理论

使用薄膜及晶硅光伏组件所在平面的太阳辐照度G 和组件背板温度T 两个因素来表征光伏组件所处的外部环境，任意一种环境状态都可以用如图1所示的坐标系中的一个点来表示。每个环境点(G,T)对应的I-V曲线数据点集设为[I,V]。

图1 环境坐标系

对于环境坐标系中的任意一条直线上的任意三点(G1,T1)、(G2,T2)、(G3,T3)，如图2 所示，其对应的IV 曲线数据点集分别为[I1,V1]、[I2,V2]、[I3,V3]，假定[I1,V1]、[I2,V2]已测量得到，需要推算(G3,T3)时的IV曲线。

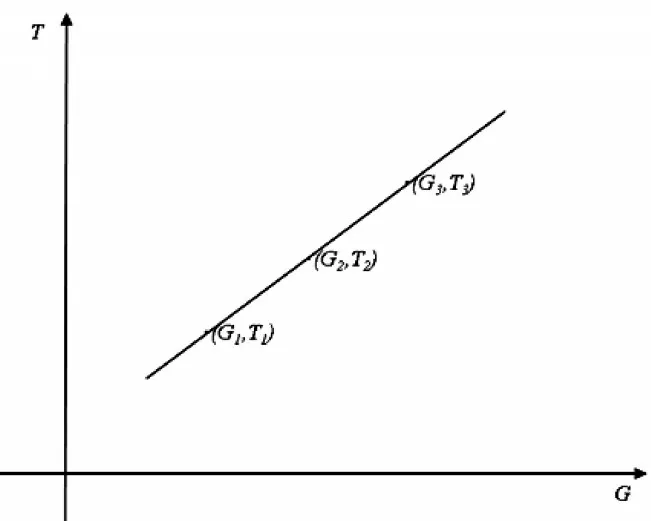
图2 环境坐标系中同一直线上IV曲线的推算方法

三点位于同一直线上，必然满足式(1)

b为计算系数，当01 时，(G3,T3)位于(G2,T2)侧外，当b<0时，(G3,T3)位于(G1,T1)侧外，称之为外推法。b越大外推越远，推算的准确性会降低。(G3,T3)条件对应的I-V曲线数据点集[I3,V3]可以通过循环公式(2)计算，其中(I1,V1)、(I2,V2)分别为数据点集[I1,V1]、[I2,V2]中的点，并且满足关系式(3)。

上述推算方法具有很大的局限性，不能推算任意环境下的功率输出，通过对上述方法进行拓展，分步多次推算，可以覆盖整个坐标平面内所有点，如图3 所示。首先通过(G1,T1)、(G2,T2)两点的IV 曲线推算(G5,T5)时的IV曲线，然后通过(G3,T3)、(G4,T4)两点的IV 曲线推算(G6,T6)时的IV 曲线，最后通过(G5,T5)、(G6,T6)两点的IV 曲线推算最终目标(G0,T0)时的IV曲线。

图3 环境坐标系中任意一点IV曲线的推算方法

2 实验部分

2.1 实验设计

因薄膜电池与晶硅电池功率推算方法基本相同，本文针对标称功率为245 W的多晶硅光伏组件展开分析，获得的结果可以认为同样适用于薄膜电池。功率测试仪采用第三方实验室AAA 标准的PASAN 瞬态模拟器，测试误差在0.5%以内。采集35 个不同条件下的IV 曲线数据，大气质量AM1.5，辐照度误差±1%，温度误差±0.5℃。根据上述理论中的推算算法，利用任意几个点的I-V 曲线推算目标点的I-V曲线，并计算最大功率，与测量得到的I-V曲线和最大功率进行比对，见图4。

图4 35个实际测试点分布示意图

2.2 实验结果与分析

2.2.1 温度恒定，辐照度变化

表1 为温度分别在30 ℃、40 ℃、50 ℃、60 ℃恒定情况下，由700 W/m2和100 W/m2数据推算出的400 W/m2和1 000 W/m2数据。

初步发现，温度恒定时，不同辐照度下功率推算的准确性较好，平均误差0.277%，最大误差0.640%，且与400 W/m2比较，1 000 W/m2条件下的功率推算结果更准确。

2.2.2 辐照度恒定，温度变化

表2为辐照度1 000 W/m2、700 W/m2、400 W/m2、100 W/m2的恒定情况下，分别由30 ℃和50 ℃数据推算出的25 ℃、40 ℃、60 ℃(1 000 W/m2时没有60 ℃数据，以55 ℃代替)的数据。

初步分析表中数据，可得到下述结论：辐照度恒定，不同温度下功率推算的平均误差为0.767%，最大误差为2.739%。与温度恒定，不同辐照度下的功率推算相比，准确性有所下降(平均误差0.277%，最大误差0.640%)，且误差较大的情况主要发生在高温(60 ℃)、低辐照(100 W/m2)等较恶劣的测试环境下，温度较低(≤40 ℃)、辐照较强(≥400 W/m2)时，平均误差0.337%，最大误差小于0.552%。

表1 700 W/m2和100 W/m2的数据推算得到的1 000 W/m2、400 W/m2时最大功率点的推算值与测量值比较

表2 通过30 ℃和50 ℃的数据推算得到的25 ℃、40 ℃、60 ℃时最大功率点的推算值与测量值比较

2.2.3 辐照度温度均变化

1）两点推算第三点

采用图5 所示方案，利用每条直线上的蓝点数据推算红点数据，在辐照度和温度同时发生变化的情况下，验证算法的准确性。本文中一共推算6点，其中内插法推算3次，外推法推算3次。

图5 功率推算验证方案

表3 为计算结果，直线2、4 中功率推算的误差较大，这可能是因为推算点为外推点，并且与已知点的距离较远。实验结果表明，3 次内插的平均误差为0.583%，3次外推的平均误差为2.933%。

因此，建议在实际应用中应当尽量避免外推的情况出现。

2）四点推算第五点

采用图6所示方案，分别选取条件(1000 W·m-2,30 ℃)、(100 W·m-2,25 ℃)、(100 W·m-2,50 ℃)、(700 W·m-2,60 ℃)围成四边形，推算A-F六点的功率。其中A-C三点为内插法推算，D-F三点为外推法推算。

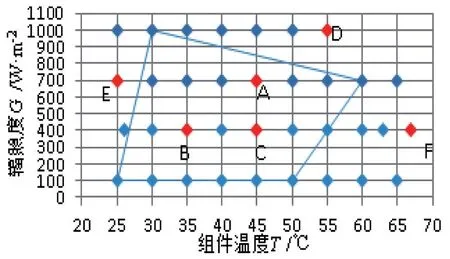
图6 四点推算第五点的方案示意图

表3 同一直线上的两点的数据推算得到的第三点情况下的最大功率点的推算值与测量值比较

表4为推算结果，可以计算出，内插三点的推算误差为0.737%，外推三点的推算误差为1.286%。显然，与两点推算第三点的结论相同，内插法推算的准确性要明显高于外推法。

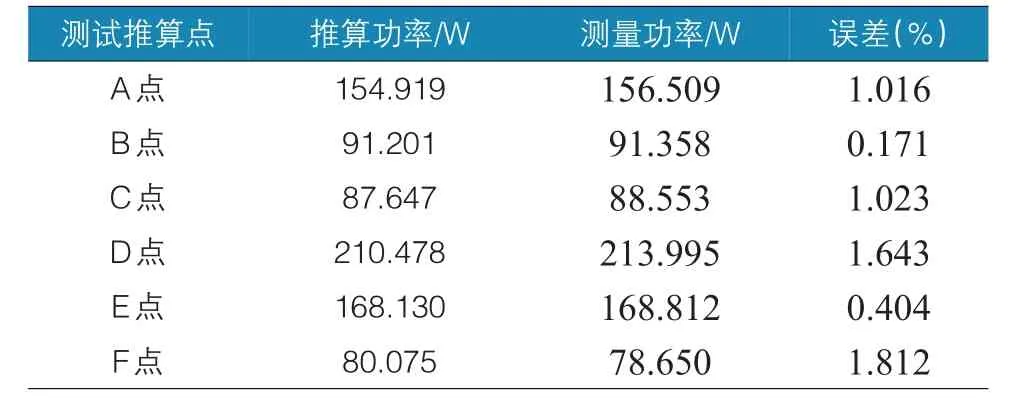
表4 由四点的数据推算得到的第五点的最大功率点的推算值与测量值比较

图7为具体的I-V曲线计算过程(实线为已知条件下测试曲线，※线为目标条件下测试曲线，×线为辅助点)：

将上述组件功率推算方法衍生到光伏阵列实际推算过程中，推算坐标见图8。对光伏阵列中组件进行抽样并在实验室中测量(1 000 W/m2，55 ℃)，(700 W/m2，35 ℃)，(400 W/m2，50 ℃)和(100 W/m2，25 ℃)4 个条件下的I-V 曲线测试数据，推算得到(700 W/m2，40 ℃)和(400 W/m2，30 ℃)情况下的组件功率，乘以组件串并联数和修正系数即可得到光伏阵列的功率输出。

图7 A-F点I-V曲线的计算过程

图8 光伏阵列功率输出推算坐标

表5 是光伏阵列的功率推算结果，从中可以看到由单块组件的推算扩展到阵列的推算并没有使推算精度有明显下降，误差基本可以保证在1%内，证明本论文提出的推算理论对于阵列的功率推算同样具有很好适应性。

表5 光伏阵列的最大功率点的推算值与测量值比较

2.3 功率推算方法对比分析

本实验室挑选了245 Wp 光伏组件进行试验，该组件的功率温度系数为-0.43%/℃。先进行暴晒预处理，性能稳定后测试其在不同辐照度和温度(Gi,Ti)下的性能，并使用(1 000 W/m2，25 ℃)条件下的实测值作为P0和Gi,ref，推算(Gi,Ti)下的名义功率，与实测值进行比较，分析结果见表6。

依据表6 中数据分析，常规的名义功率的计算上存在不稳定误差，平均误差约2.14%，且大误差出现在低辐照度情况下，其误差来源大致有：

将最大功率与温度的关系近似为线性，这仅在标称温度附近成立；

将最大功率与辐照度的关系近似为线性，实际情况是仅短路电流Isc与辐照度成线性关系；

将温度与辐照度的修正单独考虑，简单的用乘积来修正，实际运行中温度与辐照度的影响是相互影响的。

由上述分析，常规方法使名义发电功率计算值偏高，会导致PR 值计算过低，尤其是在低辐照度和高温情况下。本文在上述推算理论的研究基础上，通过实验数据分析了任意条件下功率推算算法，并进行误差分析，该推算法更适合名义功率的推算过程。

表6 常规算法名义功率推算值与实测值的误差分析表

取预处理后的光伏组件，在实验室中测试(700 W/m2，35 ℃)、(1 000 W/m2，55 ℃)、(100 Wm2，25 ℃)和(400 W/m2，50 ℃)条件下的峰值功率，并采用该算法，分别计算了其它辐照度及温度条件下的功率，并与实测功率进行对比，见表7。

通过最大程度的减少计算误差，该算法的组件功率的推算结果具有很好的精度，平均误差仅为0.53%。对于同一光伏系统，在测得现场组件的实际标称功率P0情况下，实际计算时，仅需将采集到的辐照度G和组件温度TC代入到算法中，即可得到实时的推算功率Pm。换算成光伏阵列的理论发电功率后，其推算出的PR值的误差相对较小，准确度较高。

表7 优化算法的名义功率推算值与实测值的误差分析表

3 结论

通过本文实验部分的研究，可以得到以下结论：

1）该算法推算的结果比传统算法的推算结果准确度更高。

2）算法更适用于温度较低(≤40 ℃)、辐照较强(≥400 W/m2)的情况。

3）外推推算的准确性相对较差，内插时的推算精确度相对较高。

4）该薄膜及晶硅电池组件功率推算理论同样适用于光伏阵列功率的推算过程。