基于POA-GA嵌套算法的小浪底-西霞院水库联合优化调度

王渤权，沈 笛，赵 珂，王建平，董泽亮

(1. 南京南瑞水利水电科技有限公司，南京 211100；2. 水利部小浪底水利枢纽管理中心，郑州 450099)

0 引 言

我国是水资源丰富的国家，拥有数以万计地河流，由于水量充沛、落差大的优势自上世纪以来相继建立了十三大水电基地，并在《电力发展“十三五”规划》中明确提出，“要加快煤电转型升级，促进清洁有序发展，积极发展水电，统筹开发与外送”等电源发展战略[1]。而在梯级水库群规模逐渐成型的过程中，如何合理利用水资源，针对不同场景有效地制定出最优的调度策略也随之成为了众多国内外学者研究的热点[2]。王丽萍[3]针对径流预报误差产生的水电站出力误差进行研究，提出了考虑出力误差的水电站优化调度模型，该结果为水电站工作人员制定发电计划提供了有效的参考；纪昌明[4]综合河流演进过程特点，提出了考虑河流演进的水库群优化调度模型，并提出了马斯京根与DPSA的耦合算法进行求解，结果表明，该模型能够有效解决锦东官地水库群水流时滞问题；彭杨[5]以水库防洪、发电、航运以及泥沙淤积作为基本目标，构建了水沙联合调度多目标决策模型，通过求解得到水库蓄水时间和库容淤积率的非劣解集，为水库水沙联合调度提供了重要的理论支撑； 李传刚[6]综合考虑了区域性电网特点，在传统模型基础上提出了考虑电网约束的水库群短期优化调度模型，结果表明，该模型能够有效表征电网特点，合理制定满足电网约束需求的发电计划；此外此外肖扬[7]、陈悦云[8]等学者均为不同场景下的水库优化调度问题做出了重要的贡献。

小浪底-西霞院水库坐落于黄河干流上，南距河南省洛阳市40 km ，北距河南省济源市30 km。小浪底水库总库容为126.5 亿m3，其中淤沙库容为75.5 亿m3，长期有效库容为51 亿m3，水库的基本任务为防洪、防凌、减淤为主，同时兼顾着发电、供水及灌溉等多项调度任务，除害兴利，是一座具有综合利用功能的水库；西霞院水库作为小浪底水库的反调节水库，位于小浪底水库下游16 km 处，水库总库容为 1.62 亿m3，长期有效库容为0.45 亿m3，以反调节为主，兼顾发电、灌溉以及供水，具有综合利用功能，于2007年 5 月底蓄水运用。小浪底水库装有6台300 MW 水轮发电机组，在电网中承担调峰、调频及事故备用任务，最大发电流量为1 800 m3/s。西霞院水库装有4台35 MW水轮发电机组。

对于小浪底-西霞院水库群而言，其每日的调度策略需要依据黄委下达的调度指令进行制定，指令主要针对小浪底或西霞院的出库进行要求。但对于下达到小浪底或西霞院水库的调度指令而言，由于对两个水库出库流量以及水位过程均未知，因此增加了发电计划的制定难度。基于此，本文以下达到西霞院的调令为例进行研究，建立考虑西霞院调令的水库群优化调度模型，并提出POA-GA嵌套循环算法进行求解，为水电站工作人员提供制定调度策略的理论支撑，进而提高水库群整体发电效益。

1 考虑西霞院调令的水库群优化调度模型

1.1 模型建立

由于小浪底-西霞院水库在调度过程中需要满足黄委下达的调令要求，因此本文构建模型目标函数如下：

(1)

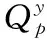
相应的约束条件如下所示：

(1)水量平衡约束。

(2)

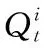
(2)水库库容约束。

(3)

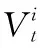
(3)下泄流量约束。

(4)

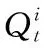
(4)出力约束。

(5)

(5)边界条件约束。

(6)

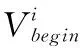
(6)非负约束。

Xt≥0

(7)

此非负限制表示上述公式中的变量均为非负。

1.2 模型求解

由于上述模型中西霞院水位过程以及小浪底出库过程均未知，因此存在双重变量共同影响发电量以及黄委调令要求。基于此，本文提出POA-GA的内外嵌套循环算法对模型进行求解，主要分为2部分：①通过POA外层循环，按照黄委调令要求对西霞院水库进行离散，形成不同组合状态下的调度策略；②通过GA算法生成西霞院水位过程，进行内层循环，寻求发电量最大的调度方案。通过内外层循环遍历最终得到满足条件下的最优发电计划及调度方案。

1.2.1 逐步优化算法(POA)

逐步优化算法(Progressive Optimality Algorithm，POA)是由加拿大学者在1975年基于动态规划算法提出的一种改进算法，主要用于求解多阶段的数值优化问题。具体而言，它将一个T阶段M维的多阶段问题分解成为T-1个子优化问题，每个子问题即为两个相邻阶段的优化问题，对于相邻时段采用逐点进行寻优，当寻得最优点时即跳转到下一个子问题继续进行寻优计算，当计算完全部阶段之后返回到第一阶段继续进行迭代，直至满足终止条件即计算结束。虽然POA算法对于每个子问题的维数仍然是M维，但由于阶段数的减少，可以有效解决动态规划所产生的维数灾问题，并且能够较快的收敛到优化调度结果。

1.2.2 遗传算法(GA)

遗传算法(Genetic Algorithm，GA)是由美国学者依据达尔文进化理论而演化来的一种随机搜索智能算法，该算法是将生物个体表征为优化问题中的一个可行解，首先在可行域内随机初始化多个个体(可行解)，即组成算法的可行解集，而优化问题中的目标函数可看做生物个体所面临的斗争，即算法的适应度函数，本着“适者生存，优胜劣汰”的原则进行筛选，能够对适应度函数表现出较佳结果的个体即视为优良个体；随后，通过对种群进行选择交叉及变异等遗传操作，不断地选出优良个体且淘汰表现差的个体，并将有利变异的个体基因以及优良个体基因通过交叉遗传给下一代，经过不断地循环迭代，层层选拔，当算法满足终止条件时，适应度函数表现最佳的个体即优化问题的最优解。遗传算法操作简单，且既可适用于连续的优化问题也可适用于离散问题，其多方向全局寻优性能对于解决当今复杂的优化问题有着很好的理论价值。

1.2.3 基于POA-GA算法的模型求解步骤

本文基于POA良好的逐阶段寻优的思想，将作用于整个调度期阶段的黄委调令分解为若干个子阶段，每个子阶段分别包含3个时刻点，通过对西霞院相邻时段的出库流量联动调整，进而保证西霞院调度策略能够满足黄委调令的要求；另一方面，利用GA算法中的初始化策略对西霞院的水位过程在可行域内进行随机生成，得到西霞院的可行方案集，通过算法高效的搜索效率最终寻得最优调度策略。基于POA-GA算法的模型求解步骤具体如下：

Step 1：划分调度期时段数T，初始化算法参数，包括小浪底、西霞院水库时段初水位Z0,0，Z1,0，西霞院调度期末水位目标值Z1,T，两个水库日均相邻时段下泄流量最大波动值ε0、ε1，西霞院水库时段下泄流量离散点M，发电量误差精度σ等，交叉率Pc以及变异率Pm。

Step 2：根据黄委调令，初始化指定水库的下泄流量过程(Qoutflow,0,Qoutflow,1,…,Qoutflow,T-1)其中Qoutflow,0=Qoutflow,1=…=Qoutflow,T-1=Qorder。

Step 3：初始化两个水库的水位过程，默认为两个水库初始均不蓄不泄，按照上述水位过程及下泄流量求得两个水库的总的发电量E0。

Step 4: 逐时段外层寻优。计算i时段与i+1时段的总下泄流量Qtotal，设定i时段初西霞院水库下泄流量变化步长，改变i时段与i+1时段的水库下泄流量，形成两阶段下泄流量联动，保证整个调度期下泄流量满足黄委调令，进而形成新的下泄流量值作为输入(输出)。

Step 5：内层寻优计算。在此下泄流量下利用GA算法初始化种群个体，即西霞院水位过程值，通过水位过程以及下泄流量反推出西霞院的水位入库过程，即得到小浪底出库过程，进而得到Step 4中下泄流量条件下的种群适应度值。

Step 6：通过GA算法交叉遗传操作对内层进行寻优计算，本文选取多父辈交叉的方法进行交叉操作，即从种群中任意挑选出K个种群个体，将其标为X1,X2,…,XK，交叉公式如下所示。

X′=a1X1+a2X2+…+akXk+…+aKXK

(8)

式中：ak为一随机系数，且有∑ak=1，-0.5≤ak≤1.5。

Step 7：通过GA算法变异遗传操作扩大寻优空间，以概率Pm进行变异操作，为保持个体的多样性，此处选取个体上的多基因点进行变异形成新的个体。

Step 8：通过选择操作选取优良个体进入下一代遗传计算，直至满足终止条件得到当前条件下的最优个体。

Step 9：改变Step 4中i时段与i+1时段的下泄流量值，继续重复Step 5与Step 8，寻求最优个体，逐时段进行寻优计算，当外层循环遍历完整的调度期后，得到最优发电量为E1。

Step 10：与E0进行比较，若E1>E0且|E1-E0|>σ，则采用当前调度策略，并令E0=E1。返回Step 4；若满足计算终止条件，则输出当前调度策略及发电计划。

模型计算流程图如图1所示。

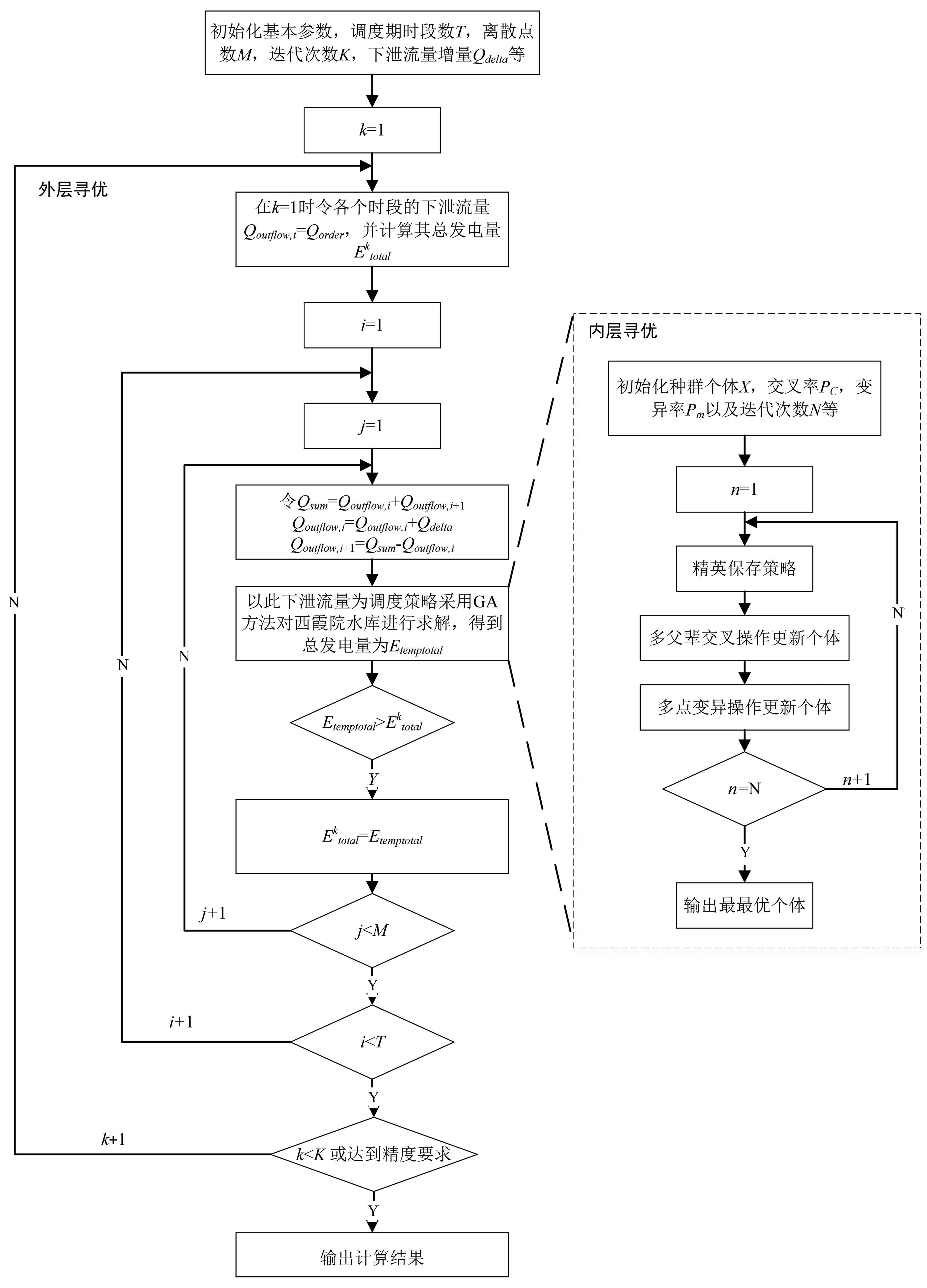
图1 模型计算流程图

2 实例分析

小浪底与西霞院水库的基本参数见表1。

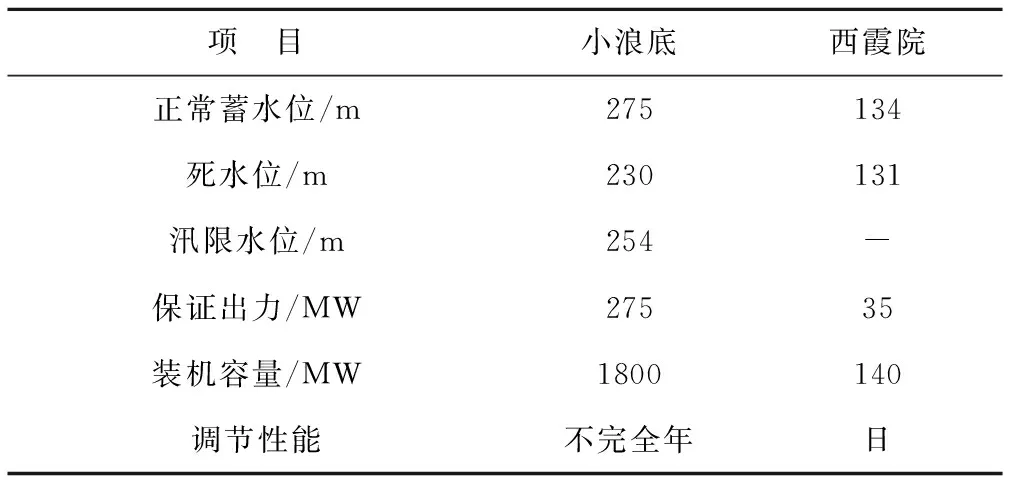
表1 小浪底-西霞院水库基本参数

2.1 梯级水库优化调度计算条件

本文选取小浪底-西霞院2018年某日数据进行仿真计算，已知该日黄委调令委西霞院水库下泄流量1 100 m3/s，西霞院调度期初与末水位均为131 m，小浪底调度期初水位为235 m，为说明本文所提方法的有效性，本文分别设置3种调度方案进行对比分析，所设置方案及详细参数见表2。

表2 3种调度方案设置及说明

其中，方案1为本文模型算法计算出来的结果，方案2即采用等流量的方法计算得到的结果，而方案3即为实际值的计算结果。

对于本文模型方法，初始化参数如表3所示。

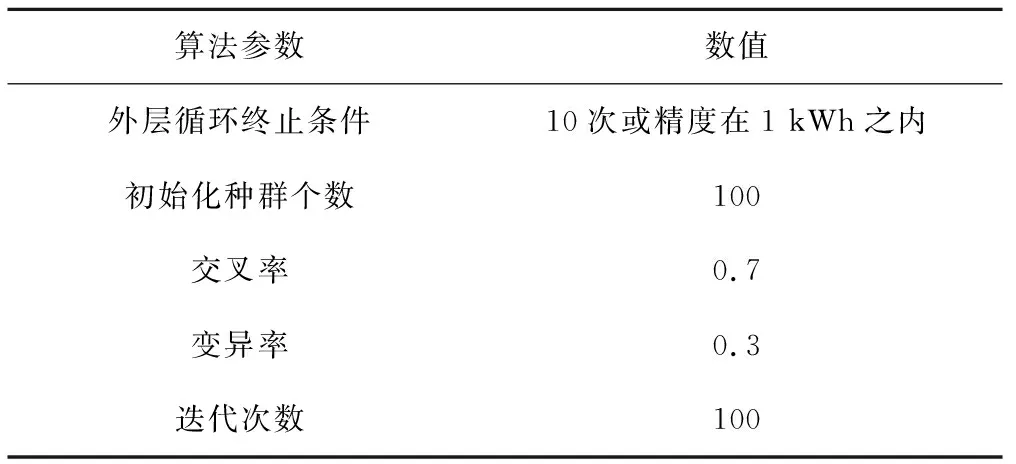
表3 算法参数初始化说明

2.2 计算结果分析

为说明内层循环的效果，本文随机选取某一内层循环结果，查看不同迭代次数下的最优发电量结果，其收敛过程图如图2所示。

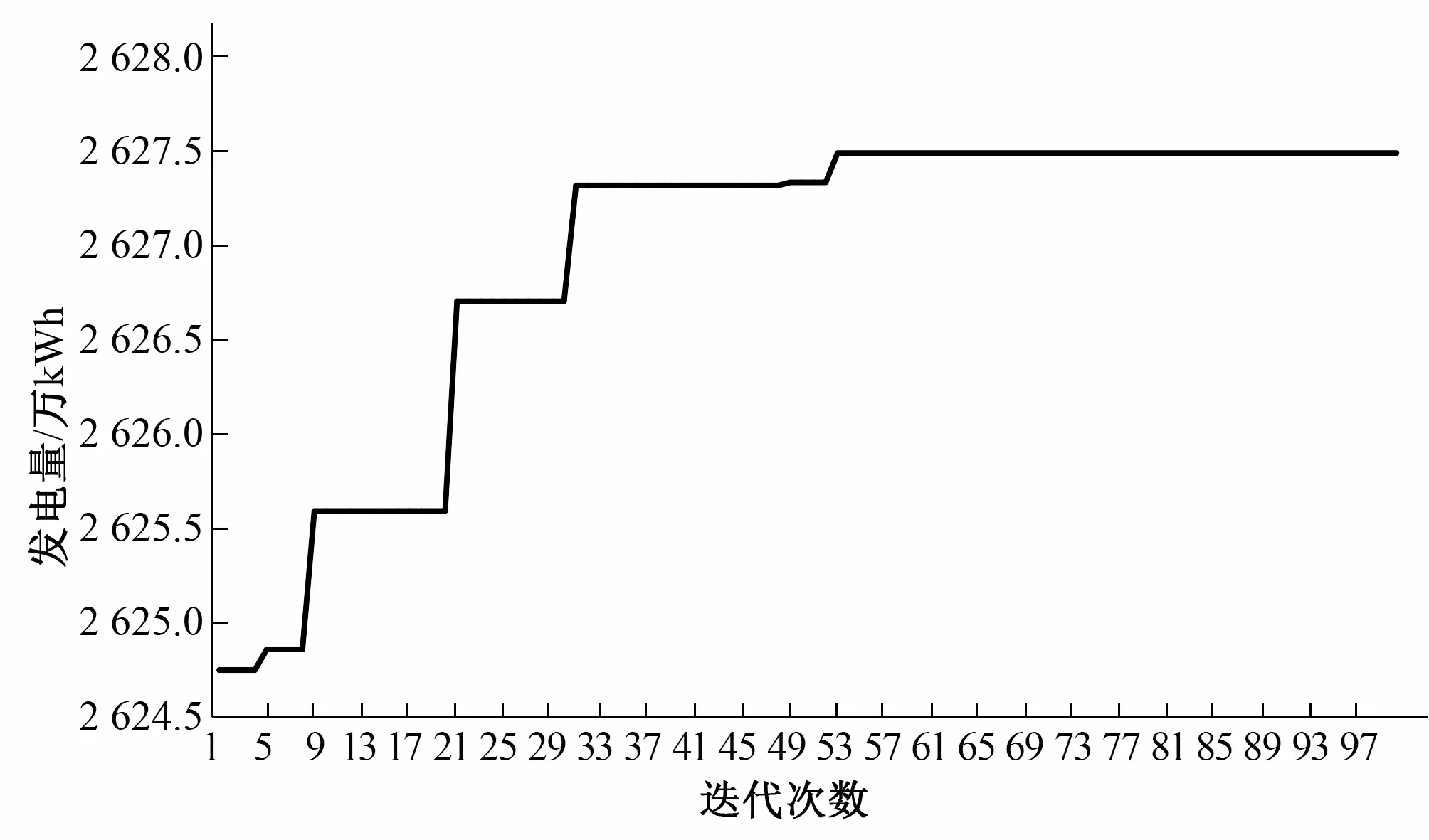
图2 不同迭代次数下的寻优过程图

由图2可以看出，在不同迭代次数下呈现出不同的寻优结果，其中在第1～5代中，其最优值为2 624.75 万kWh，随着迭代次数的增加，其最优发电量也在逐渐增加，虽然偶尔会陷入局部解的情况，但基本在较短的迭代次数下均可以重新获得最优值，由于是短期优化调度，因此其可行域范围较小，采用GA在可行域内搜索效果明显，在第100次迭代次数时最优值为2 627.49 万kWh，且可以看到基本在第60次左右即可趋近于稳定，同时考虑到算法的计算效率以及短期调度的特点，因此本文选择100次迭代是可行且合理的。

由于对于外层循环的不同阶段均存在着不同的最优值，外层循环主要为西霞院下泄流量策略的寻优，对于不同阶段而言，均存在最优下泄策略，本文通过对最后一次外层寻优结果进行统计对比，得到外层循环的最优值演进过程见图3。

图3 不同阶段下的发电量寻优演进过程图

由图3可以看出，最优值演进过程呈现出递增的趋势，起始最优发电量为2 626.41 万kWh，随着下泄流量的改变，其最优值出现差异，通过层层遍历，最优发电量最大可达2 701.94 万kWh，较起始最优调度策略增发2.8%(75.53 万kWh)，由此可以得出，本文外层寻优具有可行性与有效性。

3种方案西霞院期末水位及出入库流量过程如图4～图6所示。

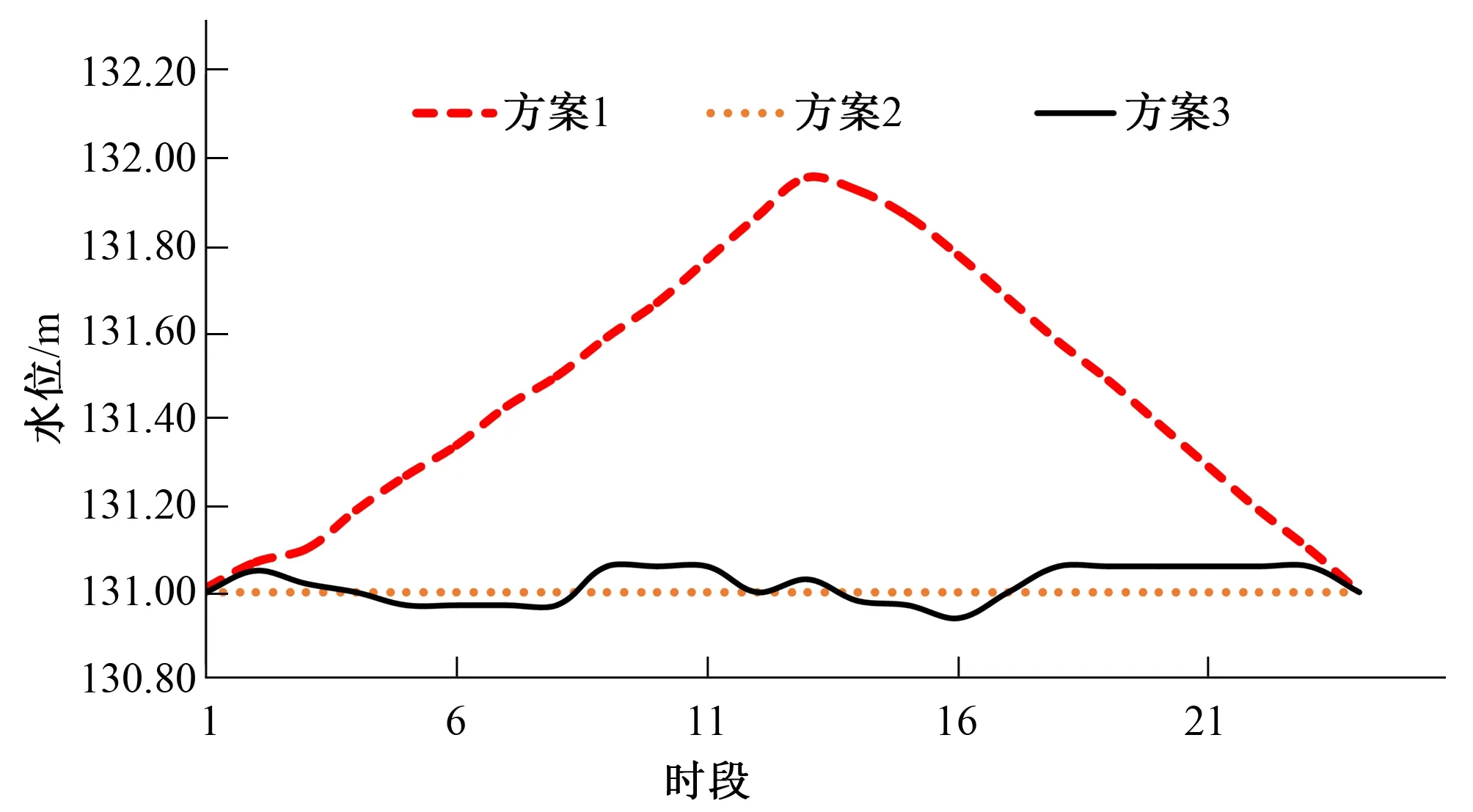
图4 3种方案水位过程

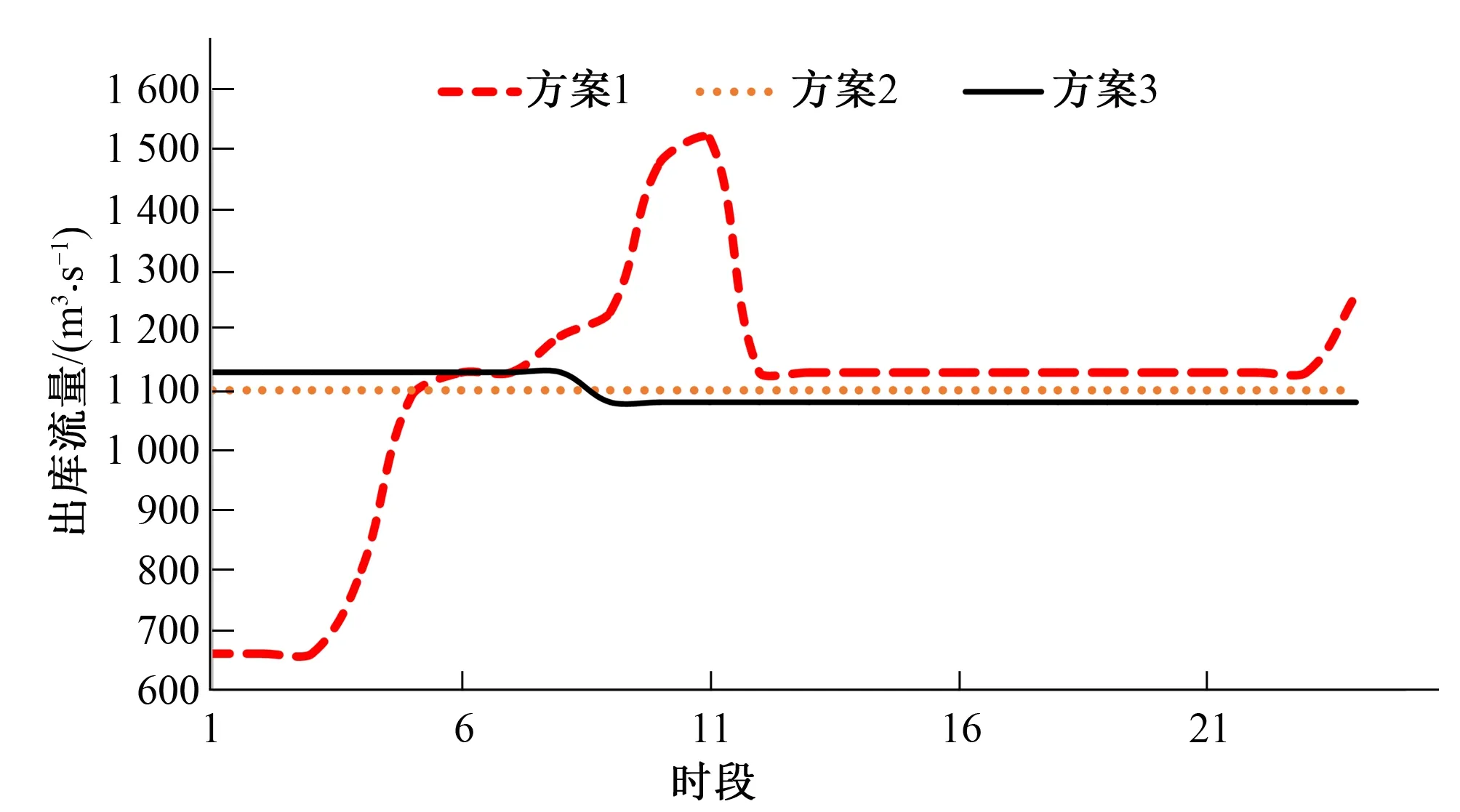
图5 3种方案出库流量

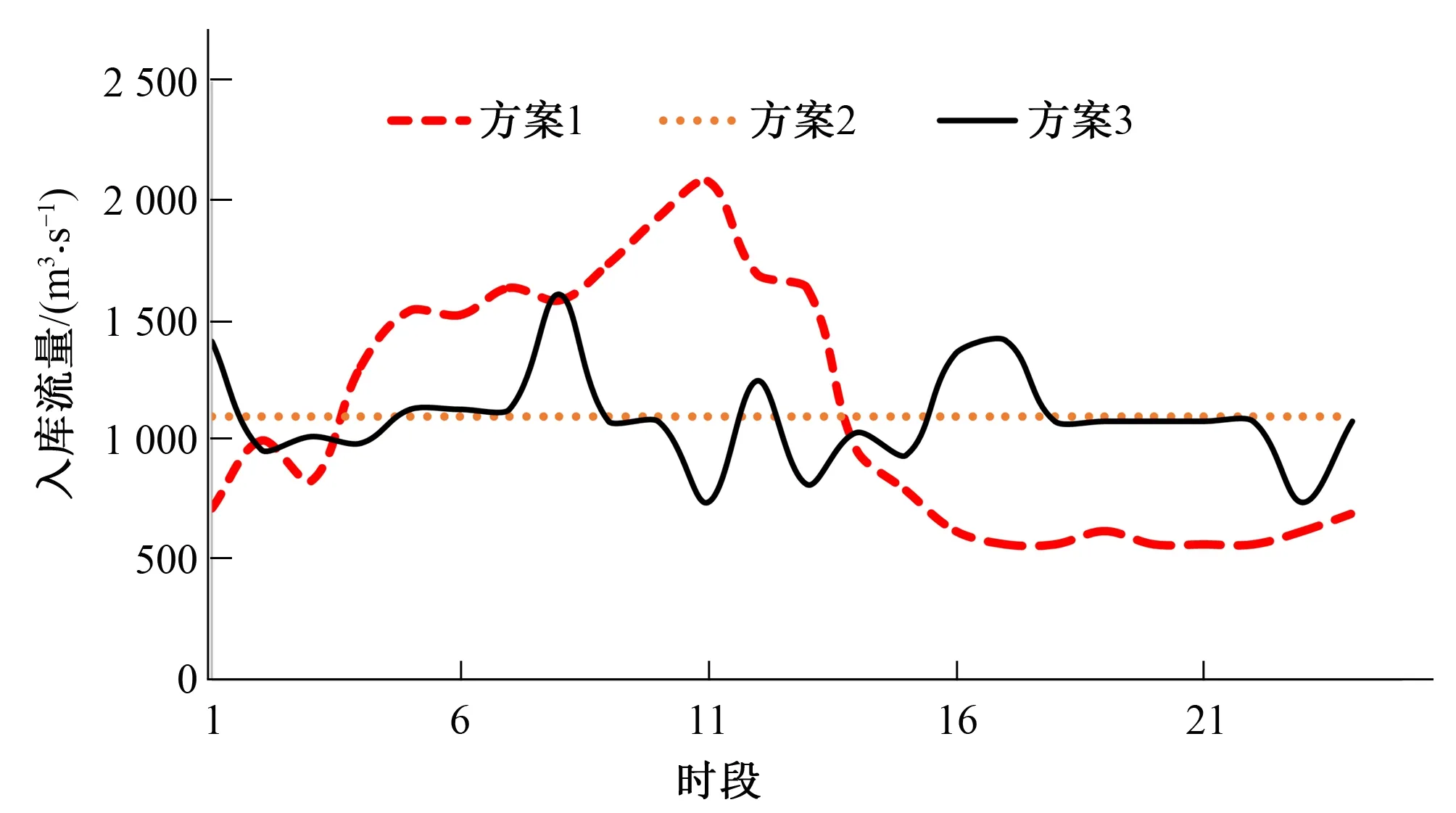
图6 3种方案入库流量

由图4～图6可以看出，3种方案水位及出入库流量各不相同，从水位过程来看，方案1水位策略为先蓄水在放水，方案2保持水位不变，即无调蓄过程，方案3在131 m附近波动(最低运行水位129 m)，3种方案中方案1能够充分发挥西霞院的调蓄作用，在调度期中水头相比于其他两种方案水水头要大，利用水头优势在下泄指标相同的情况下可以有效增加发电量。从出入库来看，方案2与方案3的出入库过程基本在1 100 m3/s附近波动，对于小浪底的调蓄影响较小，而对于方案1而言，其出入库变化过程较大，这是由于在外层POA嵌套寻优过程中，将西霞院下泄指标联充分离散，针对每种情况进行内层GA搜索，并针对每一次循环均将最优解保存下来，这样通过迭代循环大大提高了对可行域内最优解的搜索能力，充分考虑两库联合优化调度的水力、电力的联系。因此方案1较其他两种方案具有更好的搜索策略。

对于前述的3种方案计算结果如表4所示。

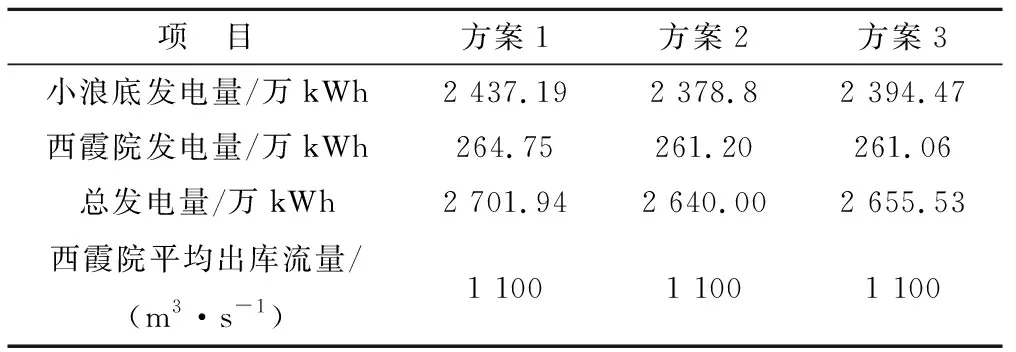
表4 3种方案计算结果

由表4可以看出，3种方案总发电量大小关系为方案1(2 701.94 万kWh)>方案3(2 655.53 万kWh)>方案2(2 640.00 万kWh)。3种方案下泄流量均为1 100 m3/s，满足黄委调令要求。其中方案2为等流量调节方式，在3种方案中发电量最小，为2 640 万kWh，这是因为小浪底西霞院水库按照等流量控制，未能充分发挥小浪底-西霞院水库群的调水功能。而方案1为本文模型得到的最优结果，不仅充分利用了水库调节库容，而且对于下泄流量也进行了寻优，因此得到的发电量最大，较实际发电量(方案三)多发46.41 万kWh，充分说明了本文模型算法较其他两种方案的优势。

综上所述，本文所提方法能够为调度人员提供科学的调度依据，提高调度精度。

3 结 论

由于小浪底-西霞院水库群调度策略需要满足黄委调令的需求，因此在制定最佳发电计划过程中会存在一定困难，为此，本文构建了考虑黄委调令的小浪底-西霞院水库群优化调度模型，并针对模型以及调度期特点，提出了POA-GA嵌套搜索的求解方法，通过外层POA循环进行全局搜索以及内层GA提高内层搜索精度。最后由实例分析得到结论如下：①通过内层循环(GA)可有效提高局部搜索精度，较初始方案值增发电量为2.74 万kWh；②外层循环(POA)可有效进行全局搜索，较初始值增发电量75.53 万kWh；③通过与不同调度方案进行对比，本模型得到的调度方案可有效水资源利用率，较历史实际值增发电量46.41 万kWh，较对比方法(方案2)增发电量共计61.94 万kWh，为3种方案最优。该模型方法可为调度人员提供科学的调度依据。