引洮供水一期工程水量调度系统的设计与仿真验证

李生钱，袁福永，毛中豪，夏 天，谈 震

(1.甘肃省引洮工程建设管理局，兰州 730000；2.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；3．南瑞集团(国网电力科学研究院)有限公司，南京 211000)

引洮供水工程位于甘肃省中部，其一期工程总干渠长110 km，设计流量32 m3/s[1,2]，工程旨在解决甘肃中部6个干旱地区的城镇生产、生活用水问题。由于工程输水距离长，取水口众多，调度管理人员需要同时控制全线几十套闸门，常规的人工调度模式难以满足工程运行管理的要求。本文在考虑沿线取水口用水需求管理的基础上，结合渠系的综合调度模型，开发了一套能够快速调节闸门，提高供水保证率的水量调度系统。

1 系统架构设计

引洮供水一期工程主要包括1处调度中心、17处现地闸门现地控制单元、34处水情遥测单元，以及现地单元与调度中心的通讯传输网络。工程沿线的闸门监控、水情信息通过传输网络与调度中心实时交互。水量调度系统软件部署在调度中心服务器上，该系统以水情、工情信息以及取水口流量需求为输入量，实时计算闸门的目标流量并经传输网络下发至现地控制单元，由现地控制单元进行闸门流量调节。系统架构见图1。

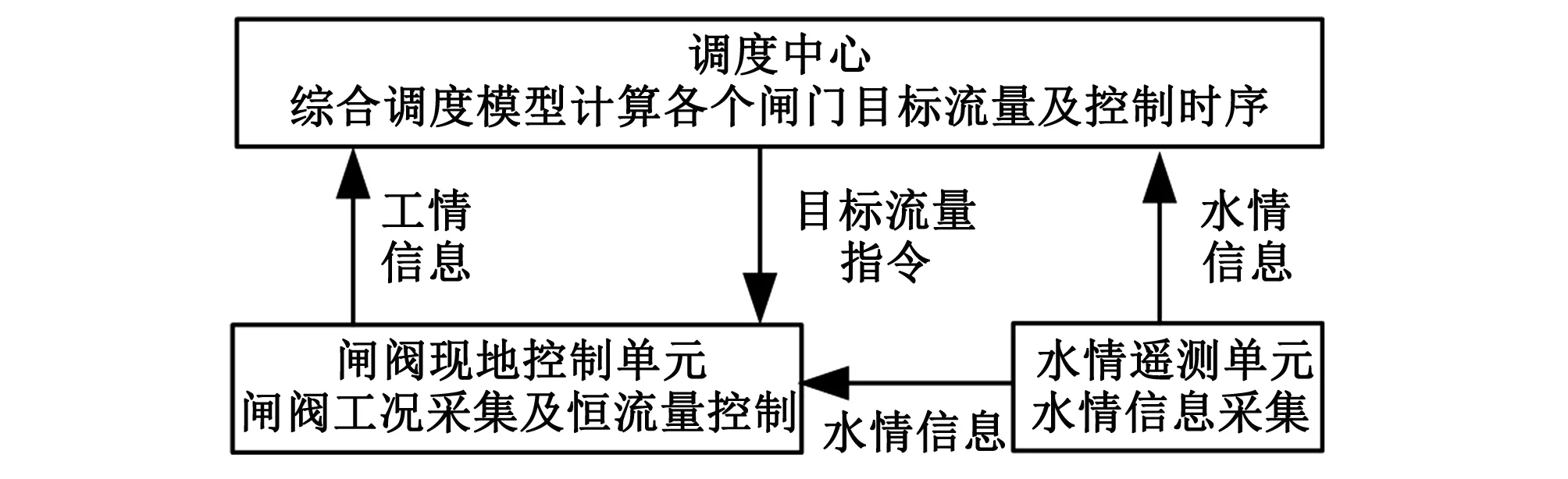
图1 系统架构设计Fig.1 System architecture design

2 综合调度模型的设计

2.1 水动力学模型

引洮一期工程总干渠沿线布置有10座节制闸，为便于对整个总干渠进行调度，将总干渠以节制闸为节点划分为9个渠池，渠池上下游处各有一座节制闸。考虑到单个渠池内的渠道有渐变段和取水口，以渐变段和取水口为节点，将单个渠池划分为若干个子渠段，子渠段按照一定的间隔划分为若干个计算断面。

2.1.1 渐变段模型

渐变段的长度相对于整个渠池的长度可忽略不计，因此将渐变段简化为节点。设渐变段起点处断面为第i断面，终点处断面为第(i+1)断面，在恒定流状态下，2个断面处的状态量可通过公式(1)和(2)连接：

Qi=Qi+1

(1)

hi+zi=hi+1+zi+1+hloss

(2)

式中：Q为断面处的流量，m3/s；h为断面处的水深，m；z为断面处的底部高程，m；hloss为水流流经渐变段的水头损失，m。

hloss由下式计算[3]：

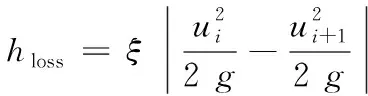
(3)

式中：ξ为渐变段节点处的水头损失系数，反映的是渐变段内部的沿程水头损失和局部水头损失之和，无量纲；u为断面平均流速，m/s；g为重力加速度，m/s2。

在已知hi+1、zi+1和Qi+1的情况下，由式(1)～(3)可得到hi、zi和Qi。其中，hloss的计算要用到ui，因此上述计算通过迭代方式进行。

2.1.2 取水口模型

与渐变段类似，取水口也可简化为节点。假设取水口起点为第i断面，终点为第(i+1)断面，则恒定流状态下，2个断面的状态量可通过以下公式连接：

Qi=Qi+1+Qout

(4)

hi+zi=hi+1+zi+1

(5)

式中：Qout为恒定流状态下取水口的取水流量，在已知Qout和hi+1、zi+1和Qi+1的情况下可得到hi、zi和Qi。

2.1.3 恒定流模型

恒定流状态下，子渠段内部各计算断面的流量相等，且沿程断面形状不变，因此只需要考虑沿程水头损失，沿程水头损失可采用下式计算：

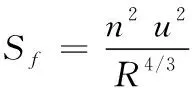
(6)

式中：n为曼宁系数，无量纲；R为断面处的水力半径，m。

缓流工况下，在已知第(i+1)断面的状态量时，其上游的第i断面处的水深可通过下式获得[4]：

(7)

式中：Es为断面比能，m；Sf为沿程水头损失系数，无量纲；在给定流量的情况下，Es、Sf都是水深的函数；S0为底坡，无量纲。

根据公式(6)和(7)，在给定渠池沿程取水口流量和下游节制闸前水深及过闸流量的情况下，可计算得到渠池内任一断面的流量和水深。以总干渠1号和2号节制闸之间的1号渠池为例，该渠池总长度2 789 m，渠池内在距离上游节制闸341 m处和1 642 m处有取水口。因此，1号渠池划分为3个子渠段，281个计算断面。假设渠池下游节制闸前水深4 m，过闸流量33.5 m3/s，2个取水口流量分别为0.24和0.48 m3/s，则1号渠池沿程水深和流量见图2。由图2可知，断面流量在取水口处发生突变，突变量为取水流量，1号渠池中不存在渐变段，因此水深不存在突变。

图2 1号渠池沿程水深和流量Fig.2 Water depth and flow along the No.1 canal pool

以总干渠2号和3号节制闸之间的2号渠池为例，该渠池总长度3 373 m，渠池内在距离上游节制闸82 m处和3 324 m处有渐变段。因此，2号渠池划分为3个子渠段，183个计算断面。假设渠池下游节制闸前水深4 m，过闸流量33.5 m3/s，渐变段节点处的水头损失系数分别为0.42和0.33，底部高程降落分别为0.05和0.03 m，则2号渠池沿程水深和流量见图3。由图3可知，断面流量沿程不变，水深在渐变段节点处发生突变，突变是由于水头损失和渠底降落导致的。

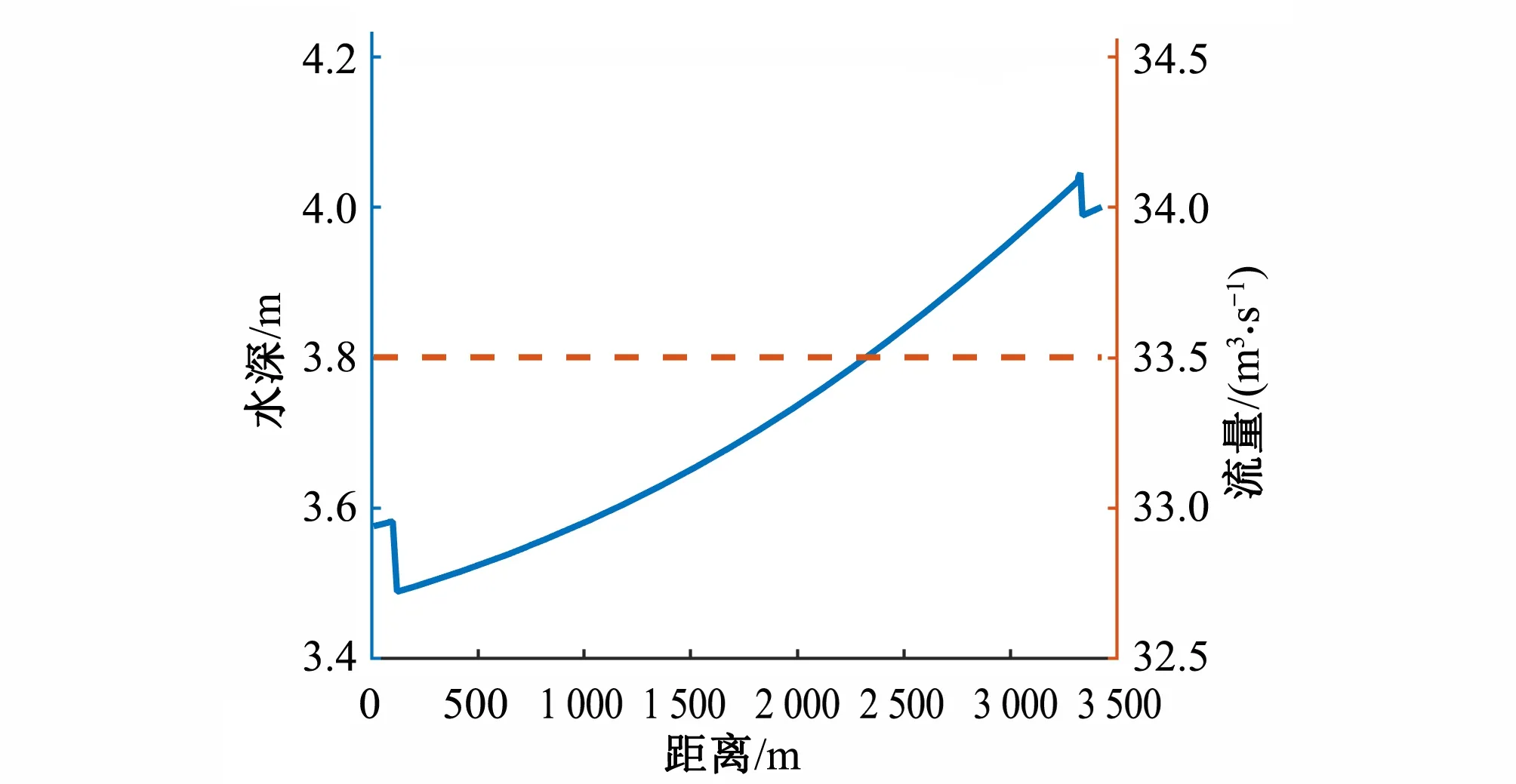
图3 2号渠池沿程水深和流量Fig.3 Water depth and flow along the No.2 canal pool

2.1.4 非恒定流仿真

明渠一维水流控制方程如下：

(8)

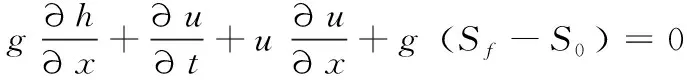
(9)

式中：B为断面水面宽度，m；x和t分别为空间和时间变量。

非恒流的求解采用隐式差分法，其基本思想是直接求解由内断面方程和边界方程组成的方程组，同时得到未知时层的所有未知量，一般采用四点偏心隐格式，即普莱士曼(Preissmann)格式[5]。

2.2 前馈及反馈控制设计

渠池中的取水口一般在渠池最下游，该处水深最大，可确保取水口过流能力满足用户需求。因此，在调度模型设计中，将渠池最下游某一点(称为控制点)的水深维持在一定的目标值附近，这样既可保证取水流量满足要求，又可降低渠道内水深变化速度，还能减少土壤中水压力对衬砌的破坏，并避免渠道漫顶[6]。为实现这一目标，需要对渠池水深采用前馈控制及反馈控制。

2.2.1 前馈控制

以1号渠池为例，前馈控制的基础是该渠池沿程所有取水口的计划取水流量以及总干渠2号节制闸的计划过闸流量。当1号渠池达到恒定流状态后，渠池内的流量分布取决于取水口和节制闸的流量。当1号渠池最下游水深不变时，渠池内流量越接近于设计流量沿程水深越大，反之则沿程水深越小。如图4所示，当1号渠池最下游水深为4 m时，流量为80%设计流量的沿程水深小于设计流量下的沿程水深。

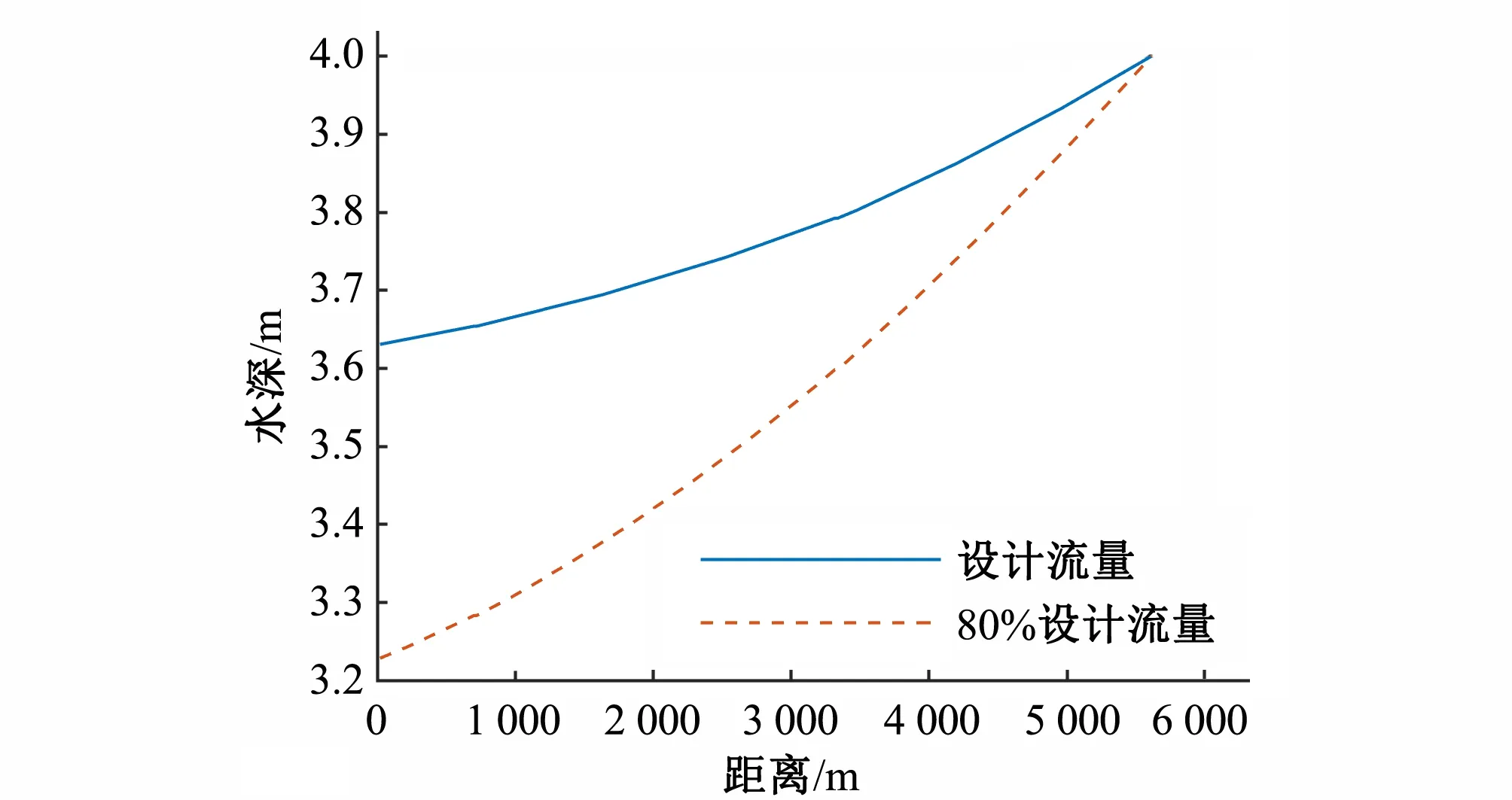
图4 1号渠池沿程水深Fig.4 Water depth along the No.1 canal pool

由于渠池距离长，断面尺寸较大，渠池内不同水深分布所对应的蓄量有很大的不同，如果单纯根据流量叠加的方式确定渠池上游节制闸的计划流量，则流入和流出渠池的流量相等，渠池内蓄量不变，稳定后必无法保证渠池控制点的水深等于目标水深。因此，在满足取水计划的基础上，还要考虑不同取水计划下渠池内的蓄量变化，这一过程称为蓄量主动补偿[7-9]。在考虑蓄量补偿的前馈控制中，1号渠池上游节制闸在下个时刻的目标过闸流量为：

(10)

式中：Vc和Vd为当前状态下和目标状态下渠池内的蓄量，m3，不同取水工况下的蓄量根据渠池内的恒定流水面线计算得到；Δt为闸门动作时间间隔。

2.2.2 反馈控制

在引洮工程中，采用PI增量控制器[10-12]，如公式(11)所示，控制器的输入为当前时刻控制点水深与目标水深之间的差值以及差值的变化速率，输出为目标过闸流量相对于当前流量的增量：

ΔQu=KpE+KiEc

(11)

式中：E为当前时刻控制点水深与目标水深的差值，m；Ec为此差值的变化速率，m/min；Kp和Ki分别表示控制器参数。

3 闸门恒流量控制的设计

闸门恒流量控制由现地控制单元实现，当调度系统将闸门的目标流量Qu下发至现地控制单元时，现地控制单元应能结合上下游水深的变化自动地调整闸门开度，使过闸流量保持在Qu，且同时能保持闸前水深相对恒定，恒流量控制分为粗调和精调2个阶段。

(1)粗调。当现地控制单元收到流量调整指令时，根据水位计实时采集的水深值，按照闸门“开度～水深～流量”关系曲线插值计算闸门开度，该开度值下发至启闭机执行。

(2)精调。受到淤积等因素的影响，通过闸门“开度～水深～流量”关系曲线得到的闸门目标开度值一般是有偏差的[13]。因此，在首次调整后，采用闭环控制的模式进行流量精调，即根据流量计实时采集的流量值Qc，用闭环控制模式对闸门开度进行调整，最终使实际流量稳定在Qu附近。精调过程中，偏差e为Qu与Qc的差值，输出为闸门开度的调整值。精调的原理如图5所示。

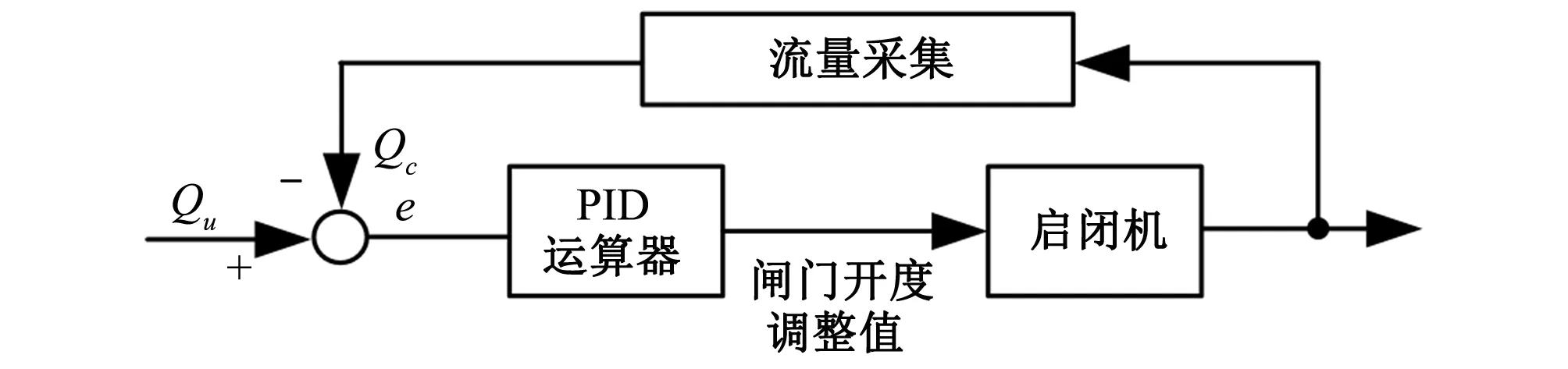
图5 流量精调原理Fig.5 Flow fine adjustment principle

选取总干渠末端节制闸前取水闸门进行恒流量控制，假设初始状态下闸门开度为0.5 m，过闸流量为1.61 m3/s，调度系统在第600 s下发目标流量1.15 m3/s，通过闸门恒流量控制，闸前水深变化如图6所示，流量变化如图7所示。当调度指令下发后，闸前水深在3.64～3.68 m波动，基本保持恒定，过闸流量在600 s内基本实现稳定控制。考虑到现场的实际情况，闸门调整的时间间隔为60 s。

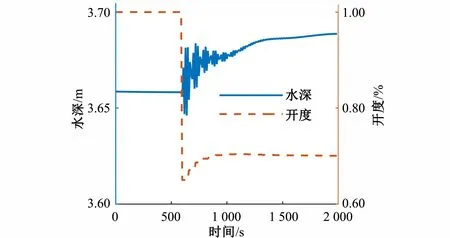
图6 取水口闸前水深过程线Fig.6 Water depth process line in front of water diversion gate

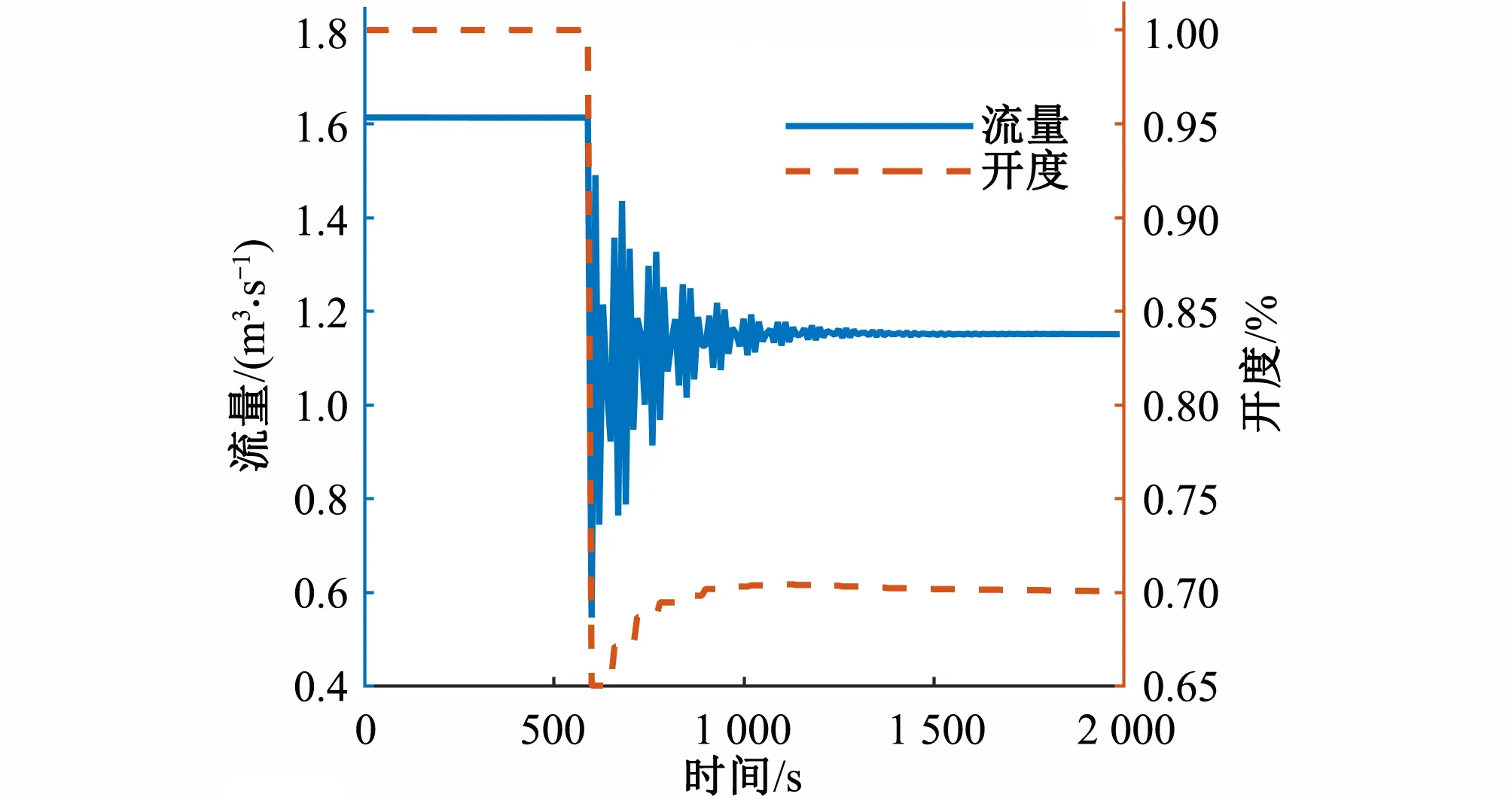
图7 取水口闸门流量过程线Fig.7 Flow process line of water diversion gate

4 典型调水过程案例

采用一维非恒定流模型，针对不同控制方式下各渠池最下游水深变化过程进行仿真。算例中，初始时刻各取水口按设计流量取水，总干渠末端节制闸流量为20.6 m3/s。取水计划调整后，沿程所有取水口流量及总干渠最后一个节制闸流量调整为设计流量的80%。所有闸门的流量变化自仿真第10 h开始，第12 h结束，期间假设过闸流量线性变化。

第1种控制方式为采用蓄量补偿的前馈控制。取水计划调整后，渠池内的流量减小，因此在维持控制点水深不变的情况下，渠池内的水面线降低，渠池内蓄量减小。考虑到蓄量补偿作用，在前馈调节过程中，渠池上游节制闸流量在一定时间段内低于下游节制闸流量和沿程取水口流量之和，此时渠池内蓄量减少，当渠池内的蓄量足以使控制点水深达到目标值时，上游节制闸流量再增加至下游节制闸流量和沿程取水口流量之和。如图8和图9所示，1～2号渠池渠首节制闸的流量在一定时间内小于最终稳定状态下的流量，随后抬升至稳定状态下的流量，控制点水深在经过开始的抬升过程后下降，并最终稳定在目标值。

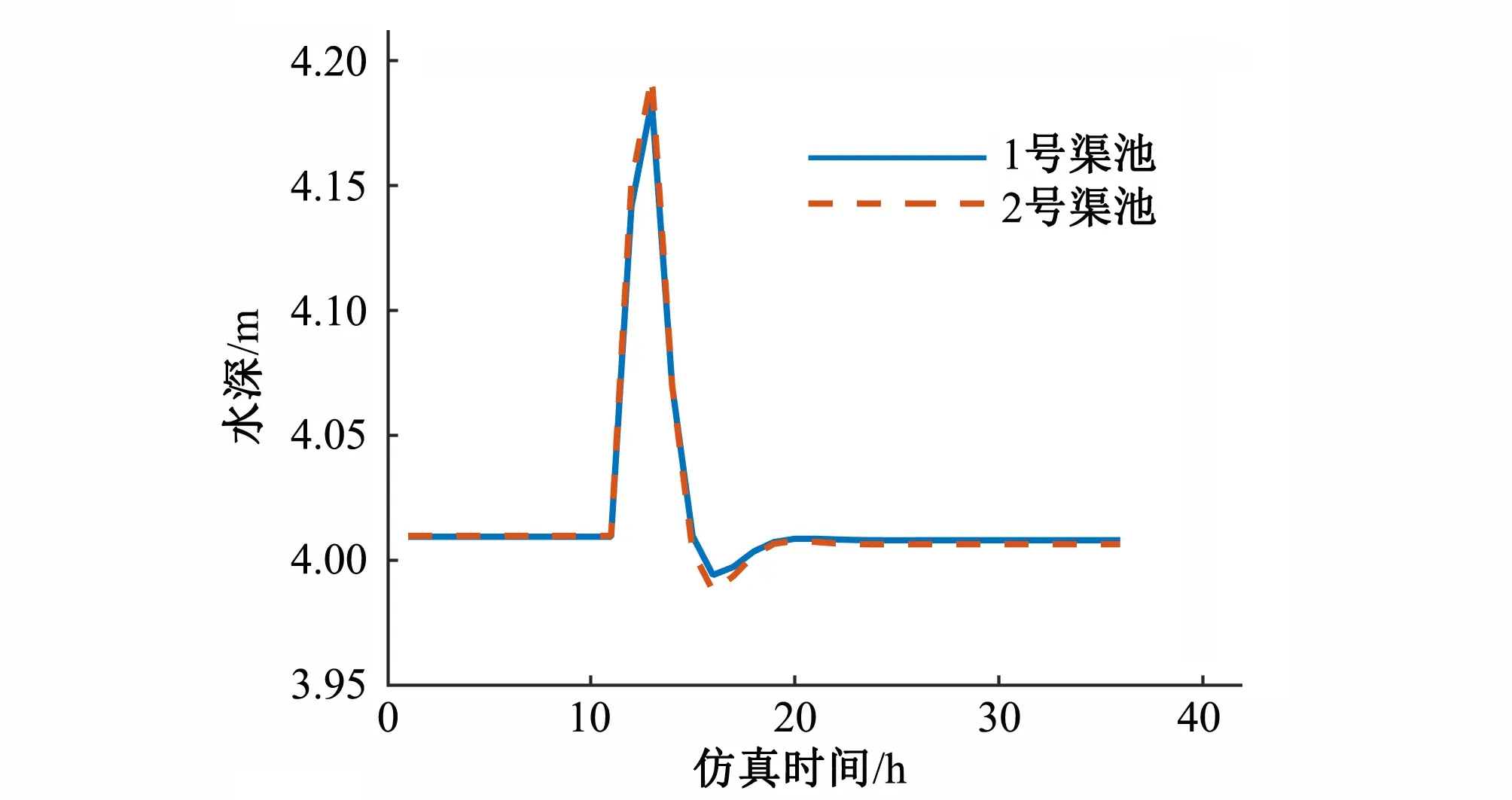
图8 1～2号渠池控制点水深过程线Fig.8 Water depth process line of control point of No.1～2 canal pool

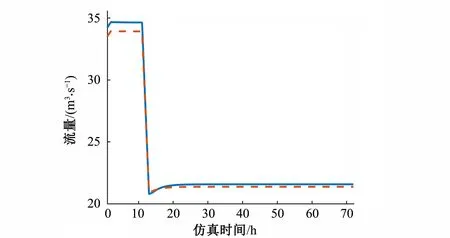
图9 1～2号渠池渠首节制闸流量过程线Fig.9 Flow process line of head check gate of No.1～2 canal pool

第2种控制方式为反馈控制。当渠池控制点水深高于目标值，反馈控制减少上游节制闸流量，反之增加上游节制闸流量，PID控制器的参数Kp和Ki分别为2和50。仿真结果如图10和图11所示。与图8相比，图10中渠池控制点的水深与目标值差值的最大值有所增加，由于PID控制器的作用，控制点水深在目标值附近波动，最终稳定在目标值。

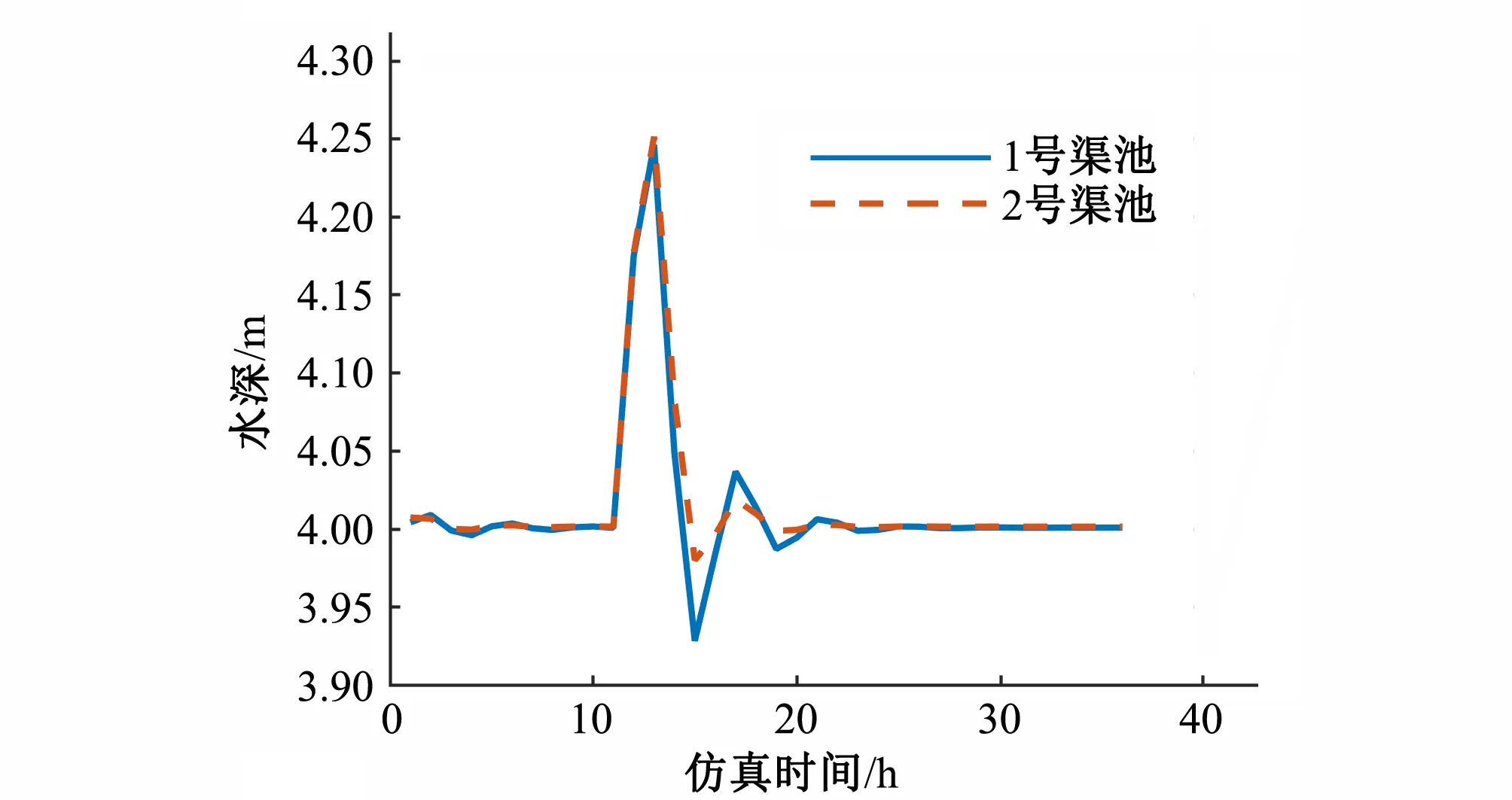
图10 1～2号渠池控制点水深过程线Fig.10 Water depth process line of control point of No.1～2 canal pool

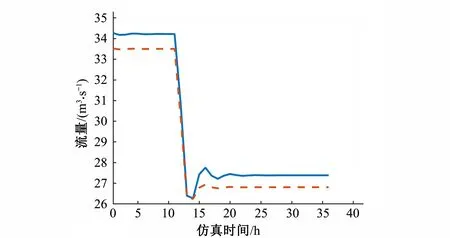
图11 1～2号渠池渠首节制闸流量过程线Fig.11 Flow process line of head check gate of No.1～2 canal pool

第3种控制方式为前馈加反馈的控制方式。此时渠池渠首节制闸的流量等于蓄量补偿下的前馈流量和反馈流量之和，PID控制器的参数Kp和Ki分别为1和25。仿真结果如图12和图13所示。与前2种控制方式相比，第3种控制方式下控制点的水深波动幅度最小，但是控制点水深稳定在目标值所需要的时间则比前馈控制略长。

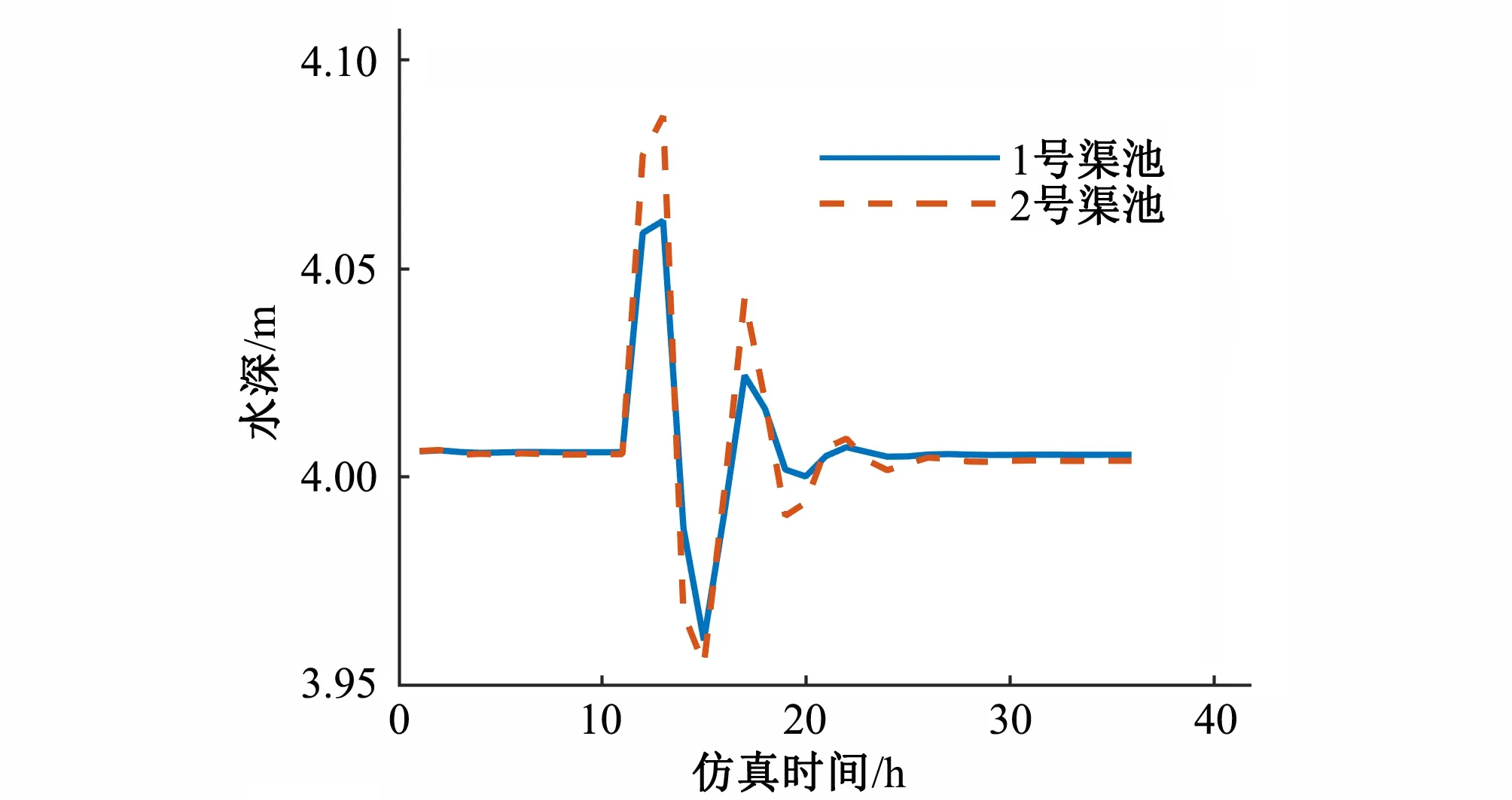
图12 1～2号渠池控制点水深过程线Fig.12 Water depth process line of control point of No.1～2 canal pool

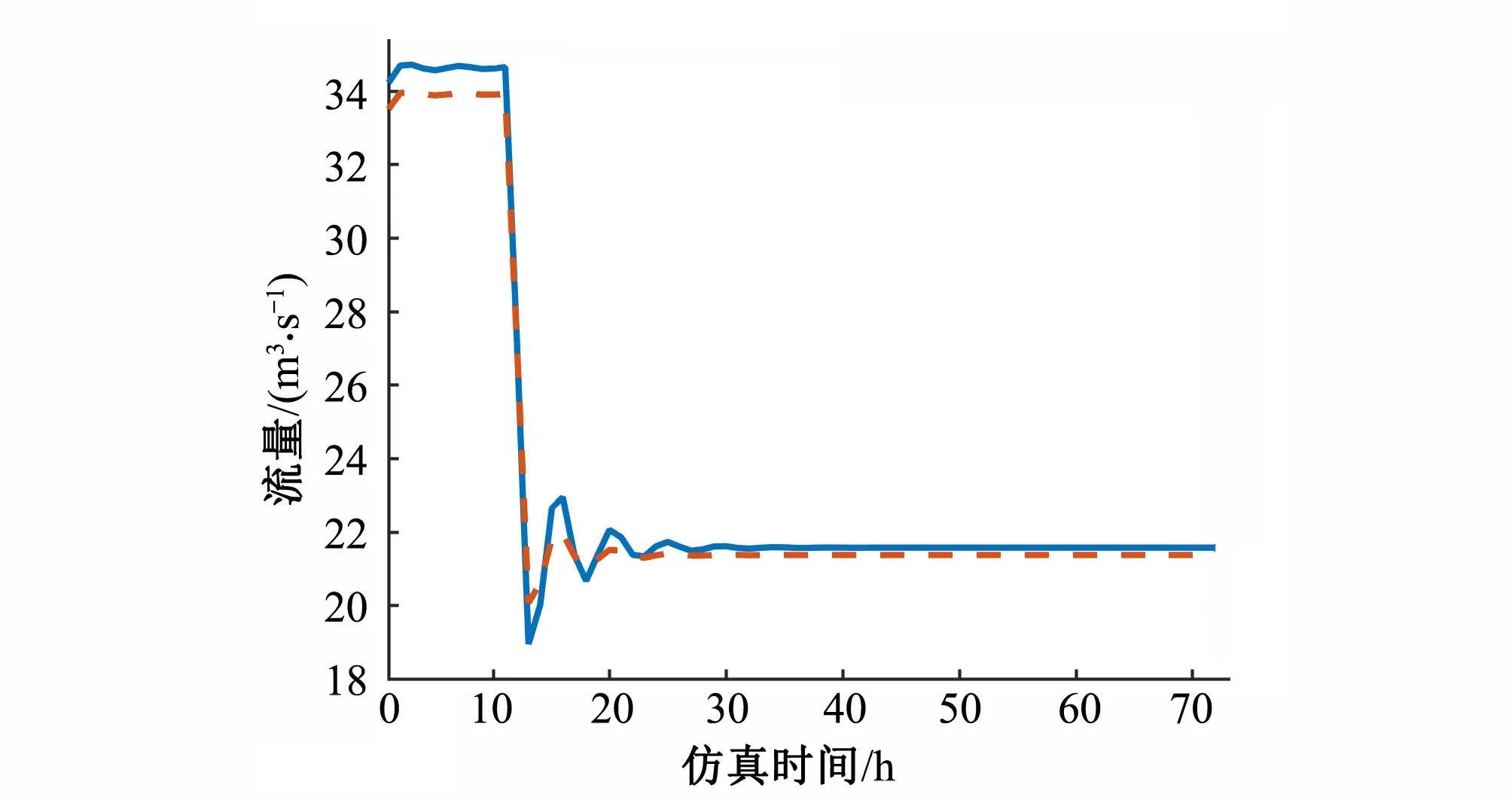
图13 1～2号渠池渠首节制闸流量过程线Fig.13 Flow process line of head check gate of No.1～2 canal pool

为衡量前馈控制和反馈控制的效果，采用控制点水深误差绝对值积分(IAE)作为衡量指标，其计算方式如下[14]：

(12)

IAE反映了控制点处的水深波动过程，其数值越小表明控制效果越好。本算例中，前馈控制下，1号渠池和2号渠池的IAE值分别为0.022 3和0.020 5；反馈控制下，1号渠池和2号渠池的IAE值分别为0.037 3和0.033 6；前馈加反馈控制下，1号渠池IAE为0.010 4，2号渠池IAE为0.012 5。综合来看，3种控制方式效果都比较好，其中第3种控制方式综合考虑了用户上报的取水计划以及渠池内控制点水深的实际变化过程，效果最好，因此在实际运行过程中推荐采用第3种控制方式。

5 结 论

引洮一期工程水量调度系统通过基于蓄量补偿原理的前馈控制和采用PID控制器的反馈控制实现了沿程各闸门目标控制流量的计算，目标流量下发至现地控制单元后，可实现流量的恒定控制。仿真算例表明，在水量调整过程中，调度系统能够减小渠道因取水变化导致的控制点水深波动，实现了渠系运行状态的稳定过渡，从而有效减少弃水，满足了工程水量调度的基本需求。