基于神经网络模型的输沙过程推估
全胜蓝,江衍铭
(浙江大学建筑工程学院水文与水资源工程研究所,杭州 310058)
含沙量过程推估及预报是水文预报中非常关键的任务,也是国内外备受关注的水文及水工议题。输沙过程合理推测和预报对于大坝设计、流域规划与管理和水土保持措施(如淤地坝修建、大规模植树造林和退耕还林、梯田建设)的制定十分重要。我国的黄河曾一度是世界上携沙量最大的河流,其独特的泥沙特征受到国内外众多专家的关注[1,2]。近年来,受到全球气候变化和人类活动的影响,黄河的径流量和输沙量均发生很显著的变化,国内有不少关于黄河水沙变化趋势及其影响因素的研究。皇甫川流域位于黄河流域中段,是黄河重要的产沙支流,研究皇甫川流域的输沙变化具有一定的典型代表意义。例如:魏艳红等[3]关注1955-2013年新时期皇甫川流域水沙如何变化,而慕星等[4]探究皇甫川流域水沙变化的驱动因素。
人工神经网络在水文预报中应用广泛、成果显著[5,6]。然而,人工神经网络对样本噪声、网络参数、网络模式等因素的敏感性,限制了它的应用和发展[7,8]。国外开始积极利用神经网络预报河流短期含沙量,如ZOUNEMAT-KERMANI M[9]利用人工神经网络方法预报河流的SSC(suspended sediment concentration);国内关于输沙过程预报的相关研究领域还处于探索阶段,主要研究以倒传递神经网络为代表的静态神经网络模型在含沙量过程推估及预报中的应用[10-12]。本文希望初步探索动态与静态人工神经网络模型在输沙过程推估方面的应用,探究其发展前景。
1 研究方法
1.1 BP神经网络概述
倒传递神经网络(BPNN)是目前应用最为广泛的神经网络模型。该模型中,输入信息从输入层经由隐含层加权运算,通过激活函数转换后,传向输出层计算网络的输出值。由于其中每一层只影响下一层神经元的状态,将其归类为静态神经网络。若在输出层无法得到目标输出值,则将其误差沿原先的反向通路回传,通过调节各层神经元的权重和偏差,直至误差达到容忍的误差范围内停止。该方法在水文预报中,尤其在径流预报方面应用颇为广泛。本文拟将其推广至含沙量推估及预报方面,探究该神经网络模型在含沙量推估及预报上应用的价值。
1.2 动态神经网络概述
静态的BPNN能够以隐性的表现方式来处理时间因子,动态反馈式的神经网络(recurrent neural network, RNN)则是以显性的表现方式将时间因子直接以回路的方式表现在网络架构中,最典型的方式是将隐含层与输出层的神经元输出值回传,作为下一阶段自身或者其他神经元的输入信息。网络架构通过这种反馈回路(feedback loop)方式产生时间稽延的效果。算法步骤如下:
网络以向前传递的当时将输入值xi(t)与对应权重wji(t)相乘累加得到netj(t),经过非线性函数变换得到反馈处理层的yj(t);将yj(t)与对应权重vkj(t)相乘累加后得到netk(t),再将netj(t)经上述非线性函数转换得到输出层的输出zk(t)。将上述过程以数学关系式表述如下:
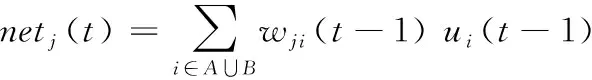
(1)
yj(t)=f[netj(t)]
(2)
netk(t)=∑vkj(t)yj(t)
(3)
zk(t)=f[netk(t)]
(4)
本文以Elman神经网络为例,这种动态反馈式的神经网络可将隐含层的神经元输出向量反馈到输入层作为输入向量,关联性单元的权重固定不变,网络可通过监督式学习与误差倒传递方法来修正其他权重。Elman神经网络是一种简单型的反馈式网络模型(simple recurrent network, SRN),可以处理相同输入形态却具有不同输出形态的不一致现象,由于链接单元提供的SRN具有动态记忆特性,即在t时刻的输入资料x(t)会跟隐含层前一时刻的输出y(t)一起进入网络,这使得网络可区分不同时刻外界环境输入资料的不同,因此对下一时刻的预测是根据当前外界环境输入因子与连接单元所提供的信息得到的。
2 研究区域与数据前处理
2.1 研究区域
皇甫川位于黄河中游河口-龙门区间的上段(见图1),流域面积3 246 km2,流域内包含十里长川、纳林川2条主要支流。皇甫川流域属于干旱与半干旱气候,流域水源主要来自降水,降雨主要集中在6-9月。流域径流量在6-9月占全年径流量的64%~99%,本文划定6-9月为汛期。皇甫川流域土壤侵蚀严重(土壤侵蚀类型可分为文砒砂岩丘陵沟壑、黄土丘陵沟壑、沙化黄土丘陵沟壑3类[4]),因此皇甫川流域水土流失严重、河流含沙量高、泥沙粒径粗,其中汛期输沙量占全年输沙量的75%~92%。在汛期遇到较大降雨时,河川流量及输沙量陡涨陡落,又因为基流很小,会形成“尖瘦”形的洪峰及沙峰。

图1 皇甫川流域水系Fig.1 Huangfuchuan basin diagram
2.2 数据前处理
本文拟构建皇甫川流域输沙推估神经网络模型,虽然输沙数据有限,但选取数据包含几十年每年最大产沙的输沙过程。研究数据为1956-2012年皇甫水文站记录中摘出82场汛期完整洪水事件(总共952笔数据),包括皇甫川水文站的逐日降雨、径流和输沙时间序列。通过相关性分析筛选后得到Q(t)、P(t-1)、P(t)、S(t-1)这4个输入变量,输出变量为S(t)。其中,水沙的相关性最好,Q(t)和S(t)的相关系数为0.67。因此将Q(t)作为模型最主要的输入因子。然而,水沙序列的自相关性不高,降雨与输沙关系一般,但对S(t)都有一定程度的影响,将其他3个输入因子作为次要影响的输入因子。本文中从摘录的82场输沙事件中挑选出74场(853笔数据)作为训练样本,8场(99笔数据)作为测试样本。将输入数据均进行归一化处理,其归一化的范围为0.1~0.9。
倒传递神经网络(BPNN)目前是应用最为广泛的静态神经网络模型。本文构建静态神经网络架构的隐含层层数为1层,利用试错法率定模型参数,隐含层神经元个数为5个,网络结构为4-5-1,构建输沙推估神经网络模型,见图2。采用matlab中newff函数构建BP模型,训练算法为trainlm。动态神经网络模型RNN,本文以Elman神经网络为例,隐含层层数为1层,使用试错法率定出神经元个数为3个,因其具有动态自记忆的特性,其网络架构见图3。

图2 静态网络BPNN模型架构Fig.2 Architecture of static BPNN model
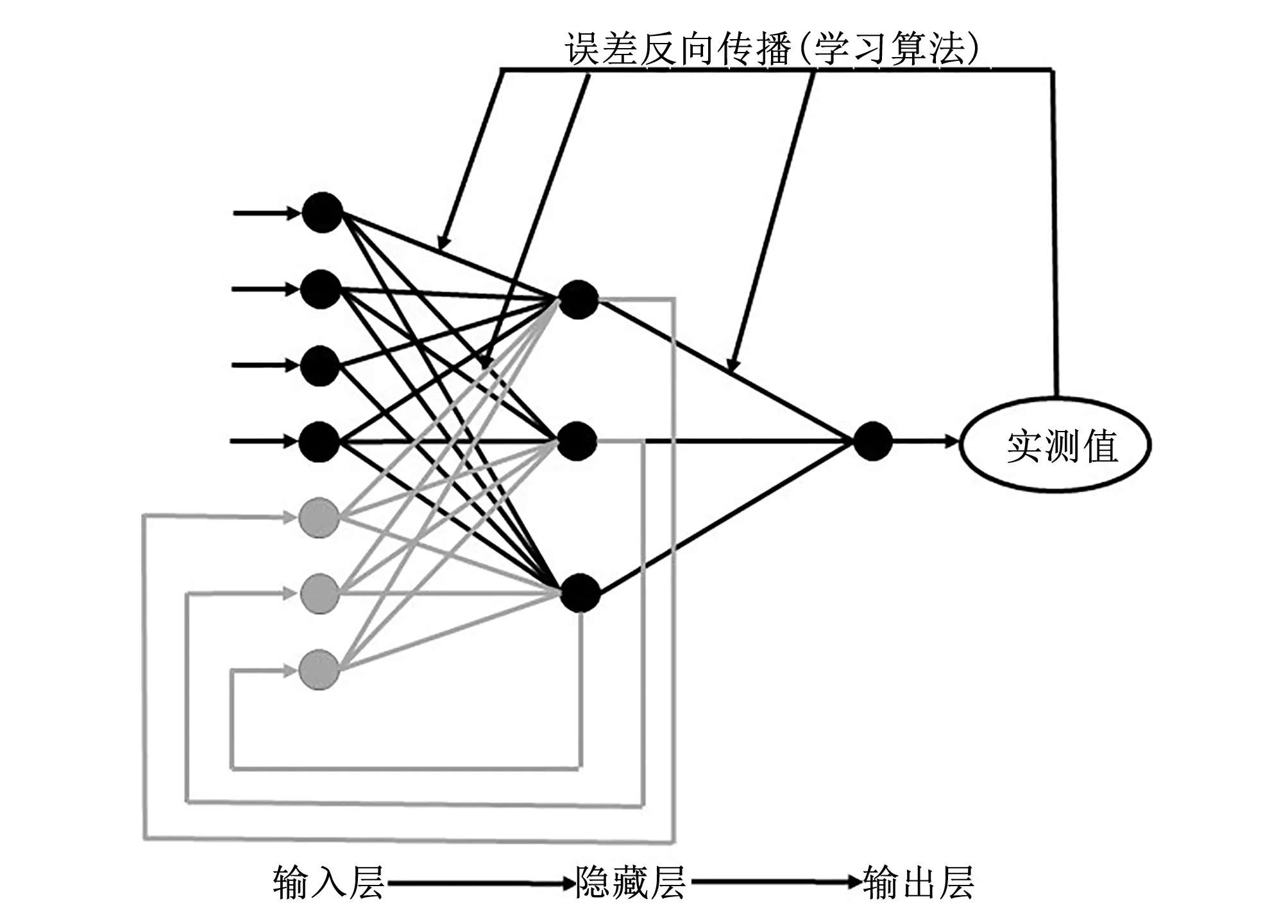
图3 动态网络RNN模型架构Fig.3 Architecture of dynamic RNN model
2.3 评估指标
关于人工神经网络模型好坏的评定指标通常采用均方根误差(root mean square error,RMSE)、效率系数(CE)以及相关系数(CC)等。
(1)均方根误差(RMSE)。

(5)
式中:N为数据组的笔数;Spre(t)、Sobs(t)分别为t时刻的预报值和实测值。
评估数值较大的观测值时,RMSE值能显著体现模型的优劣,RMSE值越小模型准确性越高。
(2)相关系数CC:
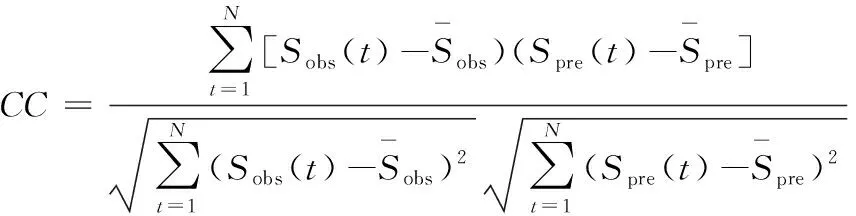
(6)
CC的范围从0到1,值越接近1说明相关程度越高。
(3)效率系数CE:
(7)
CE的范围从负无穷到1,值越接近1则精度越高。
由于黄河流域的含沙量的影响因素十分复杂,并且在水文预报领域中含沙量预报与推估的发展仍未成熟,目前缺乏对输沙量推估与预报结果的合理衡量标准。因此,本文中除了采用人工神经网络模型的以上3种常用精度指标之外,同时也采用径流预报中的常用精度指标对输沙过程进行评价[11]:
(1)沙峰评定。主要针对输沙过程的输沙峰值、沙峰滞时和沙峰相对误差。
(2)过程评定。比较推估的输沙过程与实际输沙过程的拟合程度,本文通过分别计算每场输沙时间序列的效率系数进行评估。
3 结果分析
基于训练及测试数据的划分,对架构的BPNN、RNN模型进行训练寻找最优参数建立较好的输沙推估模型。其中,BP神经网络的学习率为0.01,训练步数为1 000 步,训练目标为10-6;动态神经网络的学习率为0.001,训练步数为5 000 步,训练目标为10-6。表1为2模型测试性能的评价指标值,RMSE、CE、CC3个指标结果说明2个模型在推估输沙过程的结果相差不大,动态神经网络RNN的指标值略微大于BPNN的结果,2者均对输沙过程的趋势模拟得不错,对输沙率的推估值误差较小。
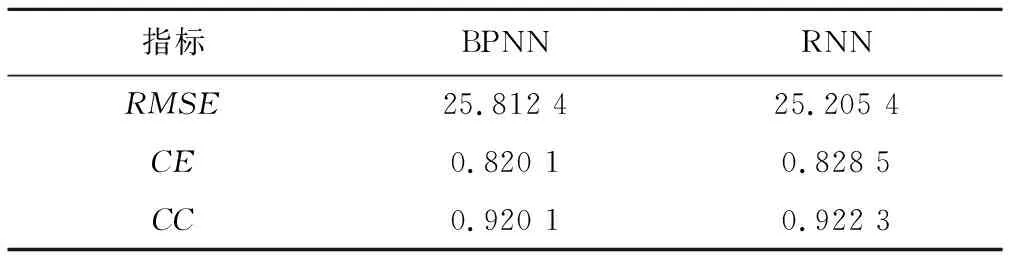
表1 BPNN、RNN模型测试性能评估Tab.1 Performance of BPNN and RNN models in testing set
图4是基于BP神经网络和动态神经网络,模型在测试阶段推估输沙时间序列以及实际观测的输沙序列。由图4可知,2个模型推估的沙峰值一般小于实际值,而模拟的峰谷值略大于观测值。2个模型推测结果进行比较可知,动态神经网络推测的沙峰值一般大于BP神经网络,更接近实际观测的沙峰值。从图4中可以发现,无论是静态神经网络BPNN还是动态神经网络RNN在拟合输沙过程的起始阶段和结尾处的峰谷值效果不佳,从而无法进一步提高模型的效率系数或模型精度。通过不断调节模型数据输入过程归一化范围,发现对输出结果与模型精度并无改进,则排除神经网络自身误差的猜测。探究认为可能原因是黄河流域特有的“小水大沙”的特征,河流在径流很小的情况下,携沙量却巨大,而在模型输入中径流是最重要的输入因子,并且径流的年内变化以及年际变化都很大,这些都为神经网络模型对输沙过程的数值模拟带来了难以消除的误差。

图4 测试集基于BPNN和RNN推估的输沙序列Fig.4 Sediment series assessment based on BPNN and RNN in testing set
BPNN、RNN 2模型对测试阶段的8场输沙过程模拟效果见图5,推估结果见表2。输沙推估和预报中,沙峰值和沙峰出现时间是评估推估模型优劣的2大指标。在测试阶段中,只有19840905 输沙序列的推测中存在1 d的沙峰滞时,其他场次无沙峰时滞问题。2个模型对沙峰值的推估结果较好,尤其是199840905和19950811这2场峰值误差不超过5%。相较而言,RNN推测值更加接近实测值,误差较小。虽然RNN在模拟沙峰值上比BPNN更好,但是从每场输沙的效率系数来看,BPNN的结果总体而言比RNN的结果要好,这说明BPNN在拟合输沙过程中退沙阶段的峰谷值效果更好。此外,除了19840905场次的效率系数分别为0.671 0和0.653 0之外,其余场次均在0.7以上,达到了预报和推估的精度要求,其中19810811和20090816的效率系数甚至在0.9以上。这些误差可能来源于皇甫川流域采取一系列的水土保持措施,包括修建淤地坝拦沙蓄水,建设梯田,以及大规模的退耕还林、植树造林。植被的改变和相关水利设施的修建会减少地表径流和河流的携沙量,增大蒸发,减少坡面侵蚀,从而改变流域地表产水产沙过程。

表2 BPNN、RNN模型测试集输沙过程拟合结果Tab.2 Results of Fitting of sediment transport of BPNN and RNN models in testing set
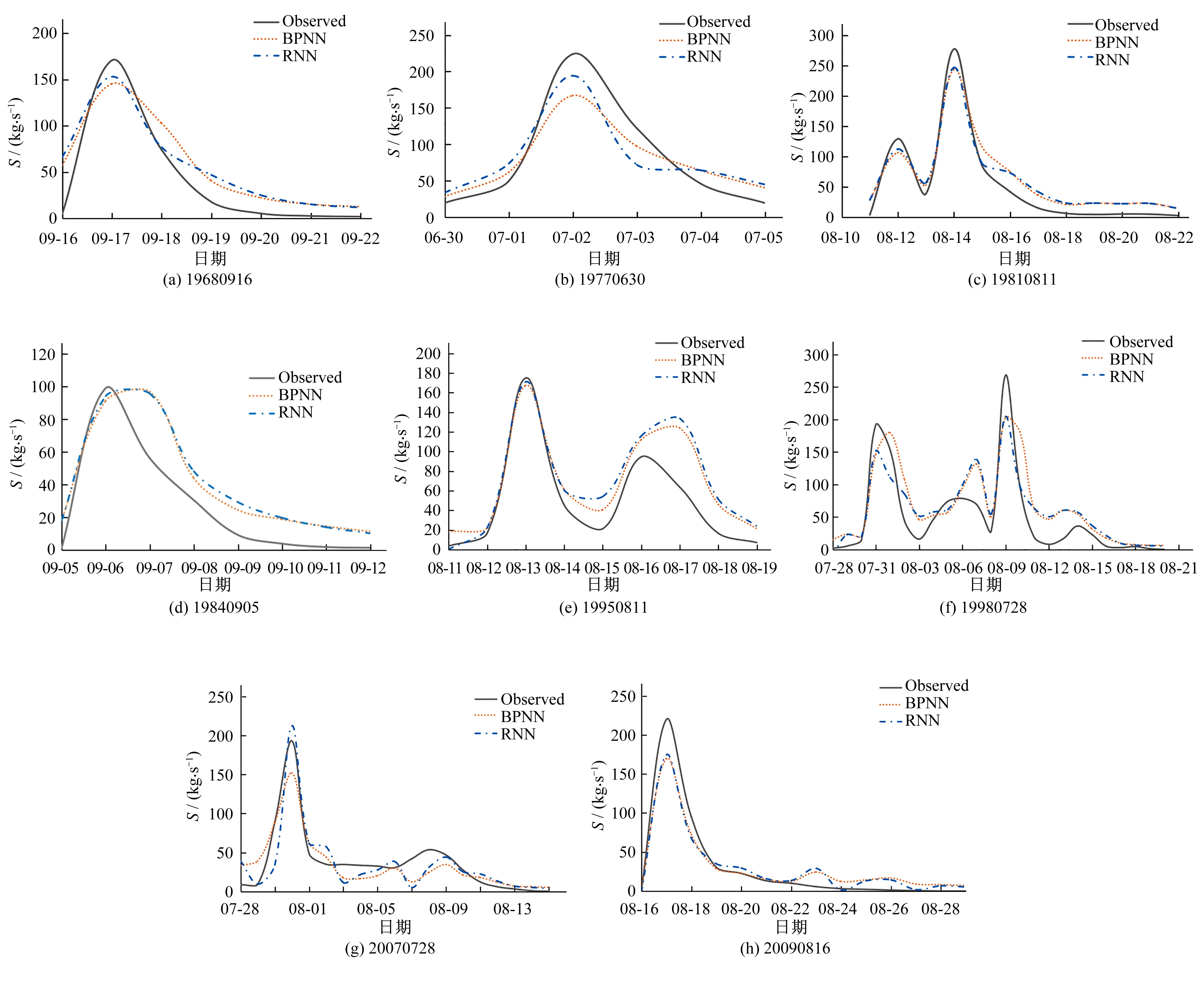
图5 基于BPNN和RNN沙峰推估Fig.5 Sediment peak discharge estimation based on BPNN and RNN
4 结 论
人工神经网络模型是水文预报中较为新颖的研究方法,广泛应用在径流预报等方面。输沙过程推估与预报也是水文预报中必不可少的一环。黄河流域的含沙量过程由于多种外界因素的影响很难估量,其输沙的推估及预报难度很大。本研究试图构建合理准确的皇甫川流域人工神经网络输沙模型。模型输入为皇甫水文站t时刻的逐日降雨、径流时间序列,以及t-1时刻的逐日降雨、输沙数据,对t时刻的输沙进行推估。可得到如下4个结论。
(1)本文以皇甫川流域为研究区域探索黄河流域中段的输沙推估模型,通过对皇甫川流域出口皇甫水文站的逐日降雨、径流以及输沙时间序列处理,以Q(t)、P(t-1)、P(t)、S(t-1) 4个变量作为模型的输入,输出变量为S(t),建立架构为4-5-1的静态神经网络输沙推估模型BPNN与架构为4-3-1的动态神经网络输沙推估模型RNN。由于水沙关系最好,因此Q(t)是最主要的输入因子。
(2)结果表明,动静态神经网络对输沙过程的推估结果较好,评价指标表明2者的推估结果差异不大,但动态神经网络的输沙推估模型模拟沙峰值的效果更好,更加接近实际的观测值。并且2个模型在推估输沙过程中,对峰谷值的模拟效果不佳,可能是因为黄河流域“小水大沙”的特征,而在本文中径流量Q(t)是模型最重要的输入因子,其年内变化与年际变化都很大,因此会对S(t)的推估产生影响,从而产生误差。输沙过程陡涨陡落,输沙基流很小,但在很短时间内涨至峰值,会对模型对整个输沙过程的推估产生影响。
(3)对推估的输沙过程进行沙峰评定和过程评定结果表明,沙峰推测值相对误差整体均在25%以内,其中19840905和19950811这2场沙峰模拟效果最好,动态神经网络模拟峰值的相对误差达到3%和2%,推估的峰值基本无滞时问题。除了19840905场次之外,其余场次2个模型的效率系数均在0.7以上,说明模型对输沙过程的拟合效果良好。静态神经网络BPNN较之动态神经网络对整场输沙过程的模拟效果更好。
(4)构建的输沙模型对于各个时期的推估效果良好,对历史数据估计与预测未来均具有良好的结果。但仍有一些无法避免的误差,误差来源于皇甫川流域植被的变化和水利设施的大规模修建,改变了流域正常的产水产沙过程,从而影响了模型的精度。如何将这些影响水沙的驱动因素加入模型是今后需要继续探究的内容。

