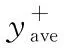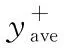y+与湍流模型对泵装置外特性计算精度的影响

沈家伟，陈松山，徐 杰，吴志峰，钱忠裕，周晓润

(扬州大学电气与能源动力工程学院，江苏 扬州 225009)

竖井贯流式泵装置是介于灯泡贯流式和轴伸式之间的一种结构形式，它将电机、减速器等置于平面近似呈纺锥形的竖井内，水流从竖井两侧流过。该装置形式结构简单，开挖深度小，便于管理维修和实现双向抽水，因此在各种低扬程大型排涝泵站工程中得到广泛应用[1]。

贯流泵内部受边界条件的影响，常伴有冲击、二次流、尾迹、马蹄涡、叶顶泄漏涡、刮起涡等复杂流动，其内部属于复杂的三维黏性非定常流动[2]。而泵装置模型试验成本高、周期长、局限多，通过CFD软件对装置内部流场进行数值模拟和性能预测，可以发现模型试验观察不出的现象甚至代替部分模型试验。泵装置流动分析的重点则在叶轮内部的旋转流动。通过流动分析，可以获得流场速度、压力、温度等物理量的分布，发现不同尺度的旋涡结构，找出能量损失的主要部位，从而为优化水力设计、提高水力性能提供依据[3]。随着流动计算方法向三维全流道黏性计算发展，湍流模型发挥着越来越重要的作用。目前可供选择的湍流模型众多，常用的有标准k-ε湍流模型和SSTk-ω湍流模型。但在壁面附近的流动情况变化很大，特别是在黏性底层，流动几乎是黏性起绝对作用的层流，湍流应力几乎不起作用，不能用高雷诺数湍流模型来求解这个区域内的流动。从工程角度看，湍流边界层脉动压力激励叶片和壳体振动，引起声辐射并增加噪声水平。因此，近壁区流动处理的好坏，直接决定着整个流场的模拟精度[4]。

1 几何模型及数值模拟

1.1 水泵装置模型

图1为本文研究的竖井贯流式泵装置模型沿装置中心线平剖面图。该泵装置模型由进水流道、叶轮、导叶和出水流道4个部分组成，各个部分的流体域造型分别在Creo中完成。叶轮和导叶选用TJ04-ZL-07号轴流泵模型，其基本参数：叶轮直径为300 mm，叶轮叶片数为3，导叶叶片数为5。根据该模型装置对应的实际泵站工程，叶片安放角为0°，模型叶轮转速n为853.3 r/min。该泵装置模型的设计流量Qdes为0.22 m3/s，选取0.8Qdes、0.9Qdes、1.0Qdes和1.1Qdes4个流量作为研究工况。

图1 沿泵装置中心线的平剖面图Fig.1 Flat profile along the pumping plant center line

1.2 基本控制方程

对竖井贯流泵装置数值模拟的基本控制方程包括连续性方程、雷诺时均N-S方程以及封闭雷诺时均N-S方程的湍流模型。

连续性方程：

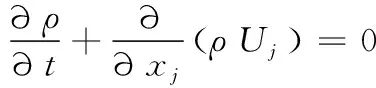
(1)

式中：ρ为流体密度；Uj为速度矢量。

雷诺时均N-S方程：

(2)

本文分别选用标准k-ε和SSTk-ω湍流模型封闭雷诺时均N-S方程。

标准k-ε模型是针对充分发展的湍流而建立的，即它是一种高雷诺数湍流模型。该模型能够较好地用于模拟某些较为复杂的流动，在流体机械中应用也比较广泛；而对于雷诺数较低的流动，特别是近壁区流动，不能直接模拟，必须借助壁面函数或其他低雷诺数模型完成模拟[9]。标准k-ε模型的湍动能k和耗散率ε的方程分别为：

(3)

(4)

式中：μt为湍流黏性系数；Pk为由于平均速度梯度引起的湍动能的产生项；C1ε=1.44，C2ε=1.92，Cμ=0.09，σk=1.0，σε=1.3。

MENTER[10]提出的基于k-ω的SSTk-ω模型是一种被广泛应用的混合模型。它在远离壁面处应用了k-ε模型，在近壁面保留了原始的k-ω模型。因此，SSTk-ω模型既可以在近壁区计算各种压力梯度下的边界层问题，也可以在远离壁面区域计算湍流运动。其涡黏系数vt，湍动能k和湍流频率ω的方程分别为：

(5)

(6)

(7)

式中：β′=0.09，α=5/9，β=0.075，σk=1.0，σω=2。

1.3 边界条件

边界条件以模型试验的实际情况进行设置：进口设置为质量流量入口(Inlet)；自由液面设置为对称面(Symmetry)；出口设置为自由出流(Opening)，并设置相对压力(Relative Pressure)为1个标准大气压；叶轮流体域设置为转速n=853.3 r/min的旋转域；叶轮与进水流道、导叶间的动静交界面设置为Stage；物理时间步长设置为60/(2 πn)=0.011 2 s；分别选用标准k-ε和SSTk-ω湍流模型；计算收敛精度设置为10-4。图2为泵装置的流体区域和边界条件。

图2 流体域和边界Fig.2 Fluid domain and boundary

1.4 网格划分

非结构化网格由一系列的四面体网格组合而成，其组合方式不具有正交性，这会打破数据结构的规律性，进而影响计算过程中算法的准确性和可靠性[11-14]。为了获得组合结构简单、更有利于数据传输的网格，本文在ANSYS ICEM中采用结构化网格对各场域进行离散化，并对所有壁面加密了边界层网格。表1为部分区域的网格最低质量、最小角度，第1层网格高度和六面体网格单元数。

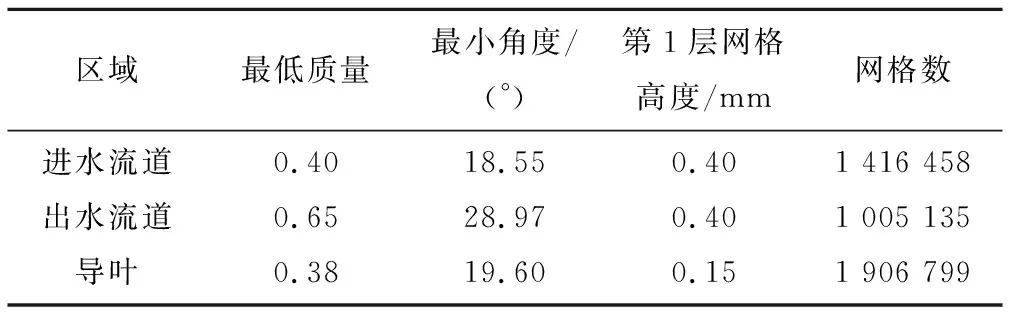
表1 部分网格信息Tab.1 Partial mesh information

对旋转机械性能来说，壁面对于仿真结果的影响尤为重要。对于有固体壁面的充分发展的湍流流动，沿壁面法向可将流动划分为壁面区和核心区(认为是完全湍流区)。在壁面区内，流体运动受壁面影响非常明显。壁面区又分为黏性底层和对数律层。为了描述壁面区内的流动，引入了一个无量纲的参数y+来表征近壁面第1层网格中心到壁面的距离：

(8)

式中：Δy为第1层网格高度；ν为运动黏度；τω为壁面切应力。

黏性底层在y+<5的区域，速度呈非线性形式；对数层的y+值范围比较宽，下限一般为11～60，上限取决于流场整体雷诺数，对1台水泵而言，上限在300左右，此时速度与距离几乎是线性关系。对近壁区域求解，主要集中在黏性子层的求解上，处理模式有壁面函数法和近壁模型法。当利用壁面函数进行求解时，只需要在湍流核心区使用高雷诺数湍流模型，在CFX 中称为Scalable壁面函数；当利用近壁模型进行求解时，通过修改湍流模型使其能够求解近壁黏性影响区域，针对不同的湍流模型有不同的处理方式，在CFX 中称为Automatic壁面函数。这2种壁面函数正好分别对应本文研究的2种常用湍流模型：标准k-ε湍流模型和SSTk-ω湍流模型。

为探究叶轮网格对这2种湍流模型模拟结果准确性和精度的影响，可根据第1层网格节点高度Δy的不同，生成了7种不同的叶轮网格方案。图3为叶轮局部网格。在叶轮壁面上，每个方案的第1层网格高度Δy各处相同；但是变化的流量工况和不规则的壁面边界导致了叶轮壁面上各处的壁面切应力并不相同，因此叶轮壁面上各处的y+值也不相同。图4为叶轮工作面和背面上y+的分布规律。在相同的第1层网格高度Δy时，径向半径越大的壁面上y+值越大，叶轮背面上的y+值也大于工作面上的。

图3 叶轮局部网格Fig.3 Impeller local grid

图4 叶轮工作面和背面上y+的分布规律Fig.4 Distribution of y+ on impeller

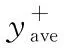
表2 叶轮壁面上的值Tab.2 The value of on the impeller wall

1.5 数值模拟的结果

对不同叶轮网格方案的泵装置模型分别应用标准k-ε湍流模型和SSTk-ω湍流模型，在ANSYS CFX上进行定常数值模拟后，通过在CFX-Post中编辑公式的方法提取预测的装置扬程h和效率η。表3为定常数值模拟预测出的装置扬程和效率。

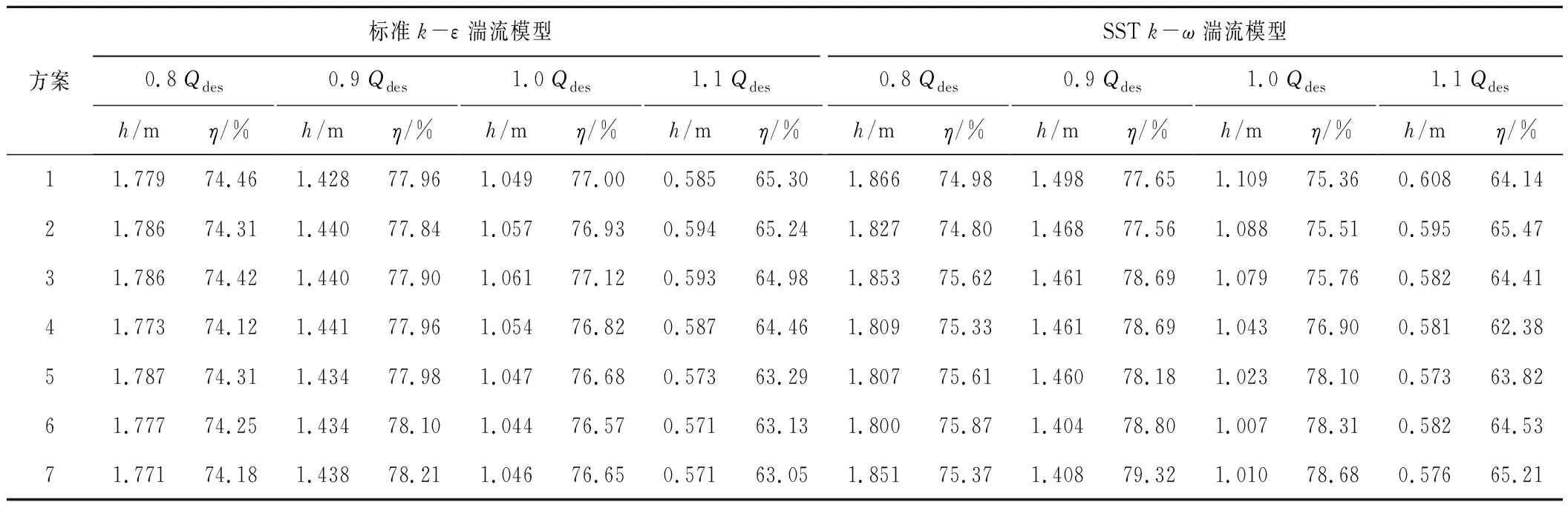
表3 数值模拟得到的扬程和效率Tab.3 Head and efficiency from numerical simulation

h=[massFlowAve(TotalPressure)@out-

massFlowAve(TotalPressure)@in]/ρg

(9)

η=ρgQh/ω[torque_z()@EntireBLADE+

torque_z()@EntireHUB]

(10)

式中：Q为泵装置的流量，m3/s；ω为叶轮转动的角速度，rad/s。

2 水泵装置性能试验

2.1 试验装置及方法

为了验证数值模拟预测结果的准确性，需要对相同的竖井贯流泵装置模型进行性能试验。同时为了探究叶轮网格y+值和湍流模型对该泵装置数值模拟外特性结果的影响并方便总结规律，可以将试验结果近似看作实际值，以其作为标准来对比各个组合方案数值模拟的结果误差。

竖井贯流泵装置模型性能试验在扬州大学流体动力工程试验室高精度泵站试验台上按照GB/T3216-2005回转动力泵水力性能验收试验标准严格进行，现试验台效率综合允许不确定度在±0.288%。试验台由水力循环系统、动力系统、控制系统和测量系统组成。水力循环系统包括泵装置模型、真空罐、压力罐、稳压罐、DN400钢管、换向蝶阀、可控开度电动阀、电磁阀等；动力系统包括55 kW直流调速电动机、辅助泵及真空泵，直流调速电动机配英国Eurotherm Drives Limited原装591C+直流调速装置及E6B2-CWZ5B光电编码器，实现高精度转速控制；测量系统包括200 N·m JC1A扭矩转速测量仪，DN400 L-mag电磁流量计，EJA系列压差(压力)传感器、CYG505高精度压力脉动传感器，TST5915动态型号分析仪、加速度传感器等；在泵装置性能试验中，通过传感器分别测量水位、扬程、流量、转速、轴功率、空化余量、温度等参数，接可编程控制器，并配备工业自动化通用组态王软件专用微机测试系统，实现试验数据实时采样和自动数据处理。所有量测设备均经过标定，并在有效期内。图5为试验现场的泵装置模型。

图5 试验中的水泵装置模型Fig.5 Device model on testing

2.2 试验结果

表4为叶片安放角为0°时该竖井贯流泵装置模型试验采集的4个研究工况的扬程H和效率ηt。

表4 外特性试验结果Tab.4 Experimental results of external characteristics

3 外特性误差对比与分析

为了直观评估数值模拟结果，比较不同方案误差大小，此引入扬程误差σh和效率误差ση，定义如下。

(11)

(12)

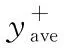
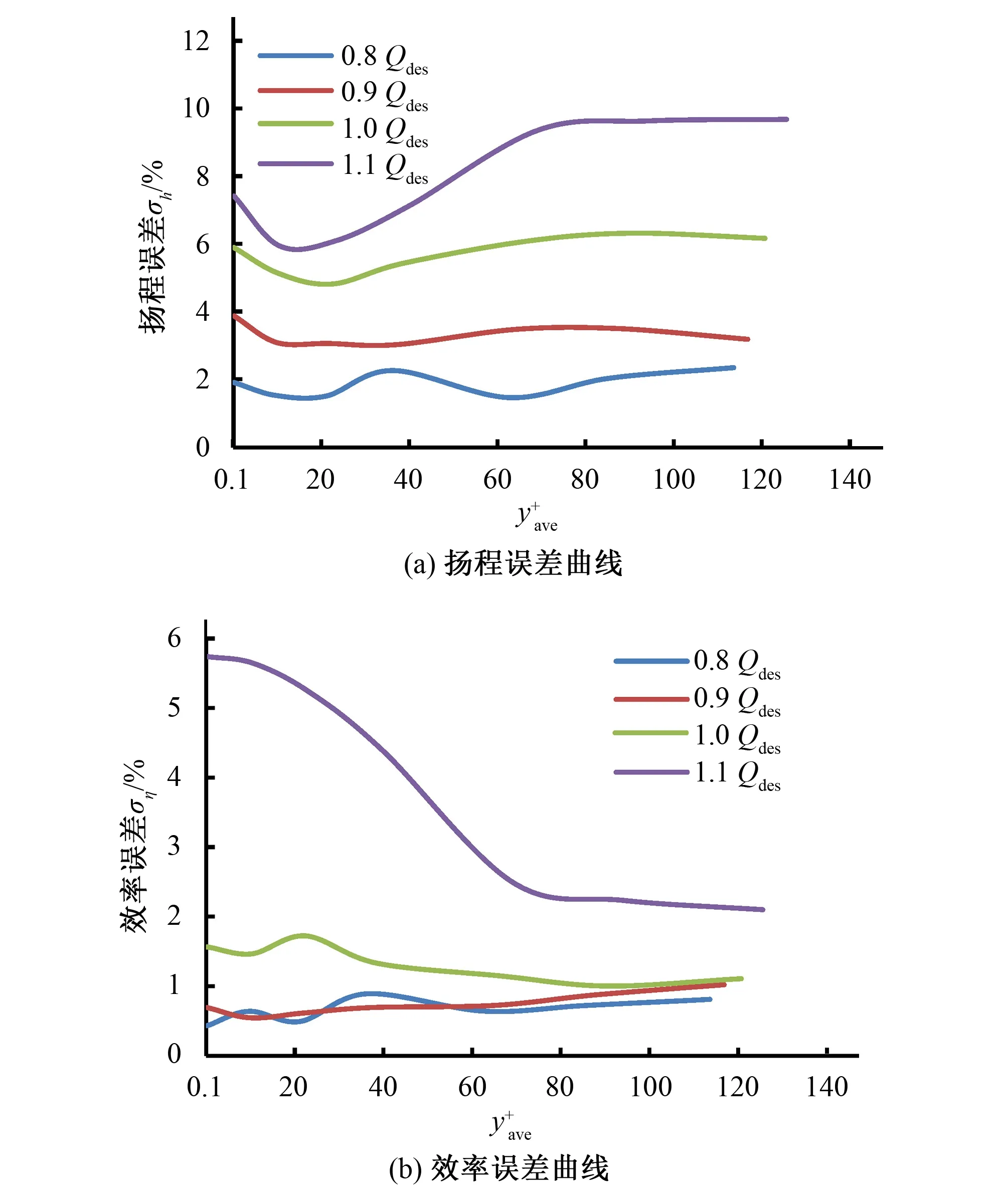
图6 应用标准k-ε湍流模型时的外特性误差曲线Fig.6 External characteristic error curve of standard k-ε turbulence model

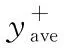
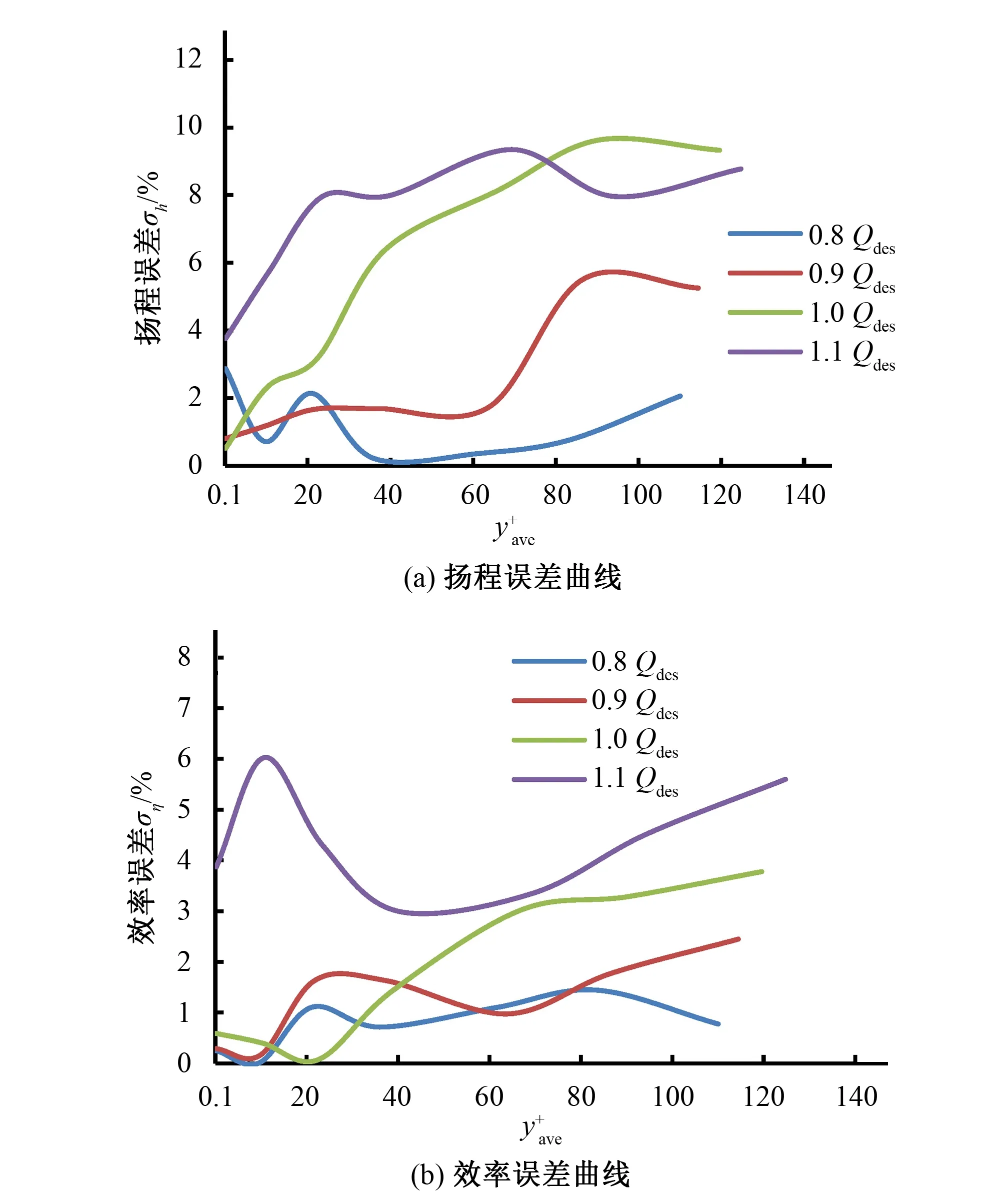
图7 应用SST k-ω湍流模型时的外特性误差曲线Fig.7 External characteristic error curve of SST k-ω turbulence model

3.2 湍流模型对外特性误差的影响

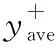
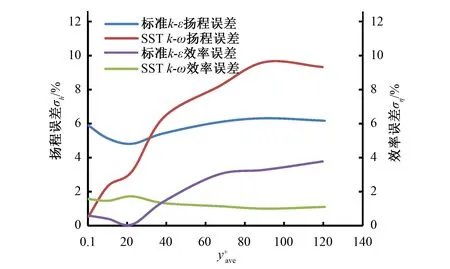
图8 设计流量下的外特性误差曲线Fig.8 External characteristic error curve under design flow

4 结 论

(1)分别采用标准k-ε湍流模型和SSTk-ω湍流模型对某竖井贯流泵装置的不同流量工况进行定常数值模拟，模拟的扬程和效率结果与试验数据误差分别在0.11m和3.72%以下。

(2)根据不同第1层网格高度Δy生成7种叶轮结构化网格，发现：y+随着位置和工况变化，径向半径越大的壁面上y+值越大，流量越大的壁面上y+值越大，叶轮背面比工作面大。