翼型最大厚度与最大拱度位置对轴流泵水力性能的影响

张 萌，石丽建，王 燕，郑宇航，梁佳辉，刘 聪

(1.扬州大学水利科学与工程学院，江苏 扬州 225009；2.扬州大学数学科学学院，江苏 扬州 225002；3.扬州大学信息工程学院，江苏 扬州 225127)

0 引 言

在轴流泵叶轮的设计环节中，叶片设计的好坏对水泵水力性能有着较大的影响，而翼型的厚度与拱度是轴流泵叶片设计的重要参数。当翼型厚度、拱度的大小及位置改变时，轴流泵的效率、扬程及汽蚀性能均有较大变化。为了尽可能提高轴流泵的水力性能，对翼型拱度和厚度进行相关研究是很有必要的。

国内外研究学者对水泵设计理论及优化方法研究较多，而针对翼型参数对水泵性能的影响研究较少。特别是对轴流泵叶片翼型厚度和拱度分布的研究较少。本文基于平面叶珊理论和CFD数值模拟方法，研究最大厚度和最大拱度的不同位置对轴流泵叶轮水力性能的影响。基于儒可夫斯基翼型，调整相关参数改变最大厚度及拱度位置，进而分析最大厚度和拱度对轴流泵水力性能的共同影响。

1 叶片设计原理

1.1 儒可夫斯基翼型

在研究叶片翼型最大厚度及最大拱度位置对轴流泵水力性能影响的过程中，翼型的选择至关重要，若翼型能够做到参数化，将对研究带来极大的方便。目前，国内大多采用“791翼型”[2]、“儒可夫斯基翼型”[17]和“NACA翼型”[18]作为水泵设计的基础翼型。其中，“儒可夫斯基翼型”结构简单，参数意义明确，能够精确控制翼型形状，便于本文中对最大厚度位置及最大拱度位置进行控制。因此，在本文的研究过程中均采用“儒可夫斯基翼型”作为水泵设计的基础翼型。

儒可夫斯基基础翼型的厚度及拱度计算公式如下所示：

(1)

式中：Ya为翼型不同位置上的拱度，mm；Yt为翼型不同位置上的厚度，mm；ε为翼型最大拱度，mm;δ为翼型最大厚度，mm；x为翼型弦长L的相对位置，其取值范围为[0,1]；当x取值为0.5时，公式表示为翼型正中间的拱度及厚度。

对翼型尾部进行加厚处理，变化后翼型厚度公式为：

Yt(x)=1.54δxc(1-x)d+3x6(1-x)0.5

(2)

当参数a、b、c、d取不同值时，翼型最大厚度及拱度大小发生了改变，本文只研究最大厚度位置和最大拱度位置的改变对水泵设计结果的影响，因此，为了使不同截面上翼型的最大厚度及最大拱度值保持不变，需要对翼型拱度、厚度公式进行变换：

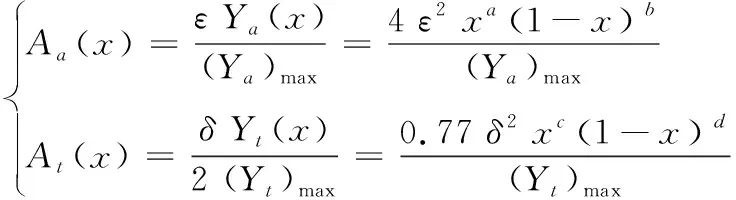
(3)

式中：Aa为调整后的翼型拱度，mm；At为调整后的翼型厚度，mm；(Ya)max为公式(1)中翼型不同位置拱度的最大值，mm；(Yt)max为公式(1)中翼型不同位置厚度的最大值，mm。

由此便得到了轴流泵叶片翼型的上、下缘曲线表达式：

Y(x)=Aa(x)±At(x)

(4)

为了研究轴流泵叶片翼型曲线表达式中参数a、b、c、d对翼型最大厚度及拱度位置的影响，进一步对公式(1)进行解析。

首先对公式(1)进行换元处理：

Ya(x)=4εXaYb

(5)

X=x，Y=1-x。

再对公式(5)求导：

(6)

令公式(6)等于0，求解得到，当x=a/(a+b)时，曲线取得最大值，即翼型最大拱度的位置在x=a/(a+b)处。同样对翼型厚度公式进行解析后发现，翼型最大厚度的位置在x=c/(c+d)处。

但由于上文对翼型尾部进行了加厚处理，导致翼型最大厚度位置与理论值之间产生了一定的偏差。因而有必要研究c+d的取值对误差大小的影响，见表1。由表1可知，当c+d≤2时，计算误差较小，而本文c+d≥2，因此可认为c/(c+d)处翼型厚度的位置最大。

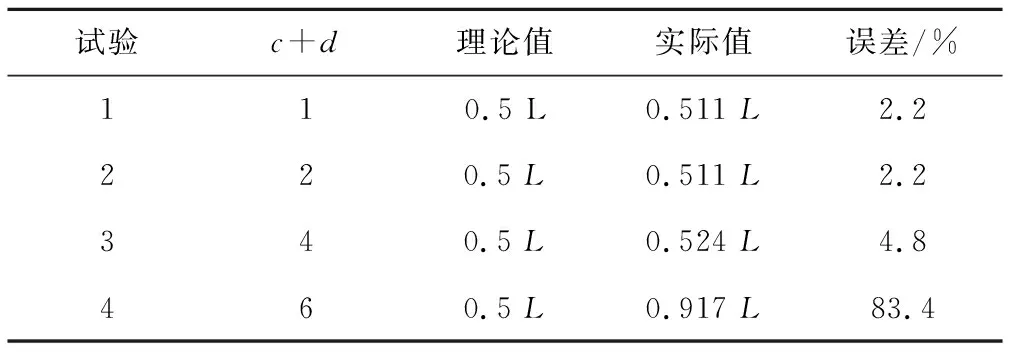
表1 参数c+d的不同取值下误差大小Tab. 1 The size of error under different values of paramaters c+d

综上所述：当a+b=2时，翼型最大拱度位置为(a/2)L；当c+d=2时，翼型最大厚度位置为(c/2)L。因此，在下文水泵设计的过程中，翼型最大拱度位置及最大厚度位置的调整将十分便捷，为叶片设计奠定了基础。

图1为叶片轮毂处截面的翼型展开图，翼型采用“儒可夫斯基翼型”，设计时a=1.2，b=0.8，c=0.5，d=1.5，此时最大拱度位置为0.6L，最大厚度位置为0.25L。

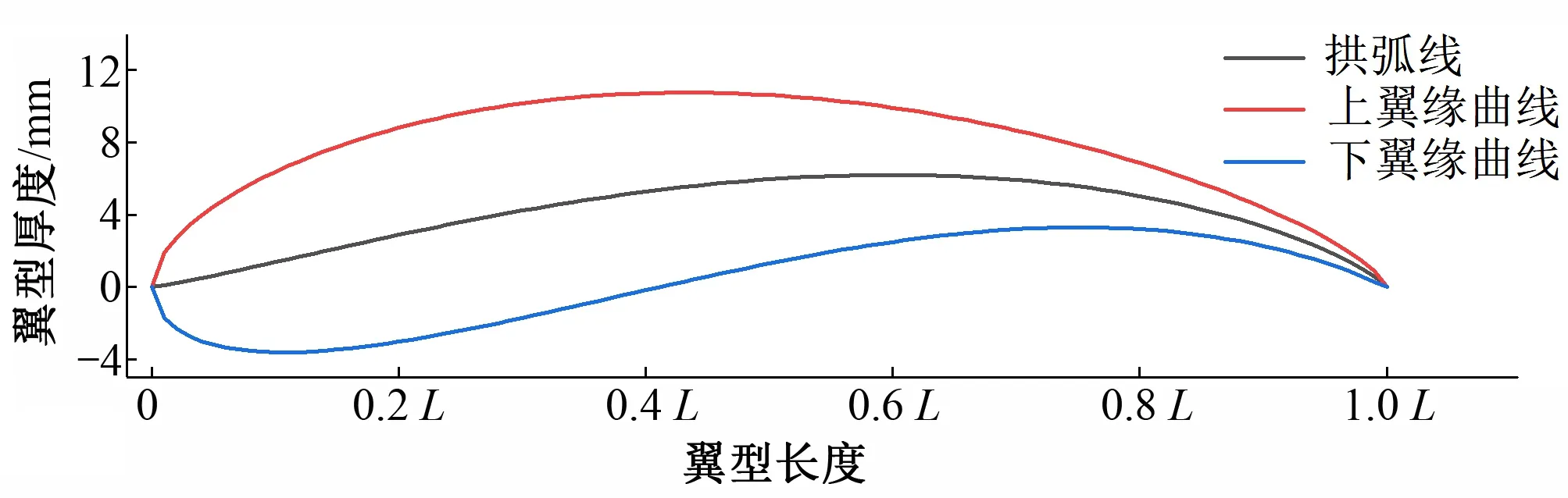
图1 参数化翼型展开图Fig.1 Airfoil parameterized unfolded-drawing

1.2 叶轮设计原理

根据实际情况确定待设计叶轮的流量、扬程、转速、轮毂直径、叶轮直径、叶片数这6个初始数据。采用平面叶珊理论，沿径向方向按线性规律取10个断面，通过Matlab程序得到叶轮不同断面上的叶栅稠密度、旋转分速度和轴向分速度[19]、叶片安放角、翼型拱度及厚度等参数的设计结果。

其中叶栅稠密度的优化根据等强度设计方法选取叶尖叶栅稠密度值和叶根叶栅稠密度值，而轮毂和轮缘之间各截面的叶栅稠密度采取抛物线分布。根据叶栅稠密度的设计结果确定叶片弦长，不同水泵叶轮设计结果的最大拱度和最大厚度值保持一致。

旋转分速度的优化有助于提高轮缘侧环量，减小轮毂侧环量，提高泵的效率[20]。可通过旋转分速度修正系数进行修正，其变化趋势为从轮毂到轮缘按抛物线分布，轴向速度为液体在轴流泵叶轮圆柱流面上的运动，可用排挤系数进行修正，不同设计结果的水泵叶轮采用的修正系数保持一致。通过旋转分速度和轴向速度的优化，可以得出叶片的进口液流角和出口液流角。为保证轴流泵在较好的状况下运行，可采用进口冲角和出口冲角分别对其修正，由此可以得出叶片进口角和出口角，2者的平均值即为叶片安放角[21]。

将平面叶珊理论设计结果通过坐标变换转化成TurboGrid可接受的三维坐标数据格式。

通过设计叶轮模型、TurboGrid画网格、CFX仿真计算等一系列手段计算出所设计的轴流泵叶轮模型的水力性能。通过对计算结果的分析，确定各项参数对轴流泵叶轮水力性能的影响大小，并以此为依据，对轴流泵模型的各项参数进行修正，同时对新的模型进行数值模拟。由此获得在初始数据条件下性能最优的轴流泵叶轮模型。图2为叶轮设计流程。

图2 叶轮设计流程Fig.2 Design flow chart

2 数值模拟

2.1 叶轮模型

本文中所设计叶轮模型的初始参数为：设计流量360 L/s，扬程5.5 m，转速1 450 r/min，轮毂直径120 mm，叶轮直径300 mm，叶片数4片。

在设计过程中，将轴流泵从轮毂到轮缘分成10个翼型断面，各断面直径分别为120、140、160、180、200、220、240、260、280、300 mm。轴流泵叶轮设计涉及到10个断面的设计参数，包括翼型安放角、叶栅稠密度、最大拱度值和最大厚度值等，这些参数在叶片设计过程中都保持不变。在本文设计模型中，10个断面的主要设计参数见表2。

表2 叶片各断面主要设计参数Tab.2 Main design parameters of each section of blade

基于上述设计参数，对叶片不同断面上的翼型最大厚度位置及最大拱度位置进行调整，得到不同叶轮模型后进行数值模拟计算。由此分析上述2个因素对轴流泵水力效率的影响，进而确定翼型最大厚度位置及最大拱度位置对轴流泵水力性能的影响规律。

2.2 网格无关性分析

本文采用Turbogird对翼型进行结构化网格划分，单通道网格数从6 万个到30 万个，共分为10组数据进行网格无关性分析。从同一模型下不同网格数的计算结果来看，轴流泵效率随着网格数的增多而逐渐增大，当网格数较小时，效率呈线性增长，且涨幅较大；当网格数达到12 万个时，网格数～效率曲线出现转折点，最终计算结果趋于稳定；见图3。从计算精度和计算效率2方面综合考虑，本文最终的单通道网格数量控制在15 万个。

图3 不同网格数下效率曲线Fig.3 Efficiency curves under different grid numbers

2.3 数值模拟

本文主要研究轴流泵叶轮的水力性能，为减少数值计算量，不对其他过流部件进行数值模拟计算。同时，为了计算的准确性，将水泵进口和出口相应延长一段距离。叶轮模型见图4。

图4 叶轮模型Fig.4 Impeller model

在数值模拟时，计算域为轴流泵叶轮。计算区域的进口为叶轮的进口，进口边界条件设置为总压，进口总压为1个标准大气压；计算域的出口为叶轮的出口，出口边界条件设置为质量流量，设计出口流量为360 L/s；叶轮单边间隙为0.1 mm；数值计算采用时均N-S方程；湍流模型采用标准k-ε模型；场域内不存在热传递、热辐射；收敛条件为1×10-6。

3 计算结果分析

3.1 翼型最大厚度位置

为了得到最大翼型厚度位置对轴流泵水力效率及汽蚀性能的影响规律，采用控制变量法，以“儒可夫斯基翼型”作为基础，仅改变翼型最大厚度位置进行研究。轴流泵叶轮设计过程中涉及到的10个断面的设计参数均保持一致，翼型最大拱度位置在翼型正中间，即0.5L处。改变公式(1)中系数c和d的取值，使得翼型最大翼型厚度位置分别处于0.1L、0.125L、0.15L、0.175L、0.2L、0.225L、0.25L、0.3L、0.35L、0.4L、0.45L、0.5L、0.55L、0.6L、0.65L、0.7L处，共计16种设计方案。

根据上述16种设计方案，利用CFD数值模拟，对不同方案下轴流泵水力性能进行分析。图5给出了不同翼型最大厚度位置下泵的扬程及效率曲线。

图5 不同最大翼型厚度位置下扬程及效率曲线(Q=360 L/s)Fig.5 Head and efficiency curves at different maximum airfoil thickness positions

由图5可知，轴流泵的扬程曲线近似线性分布，最大厚度位置位于翼型前端时，扬程下降并不明显；当最大厚度位置移动到0.3L右侧时，扬程随着最大厚度位置的增大急剧下降。轴流泵的效率曲线呈抛物线形分布，当最大厚度位置在0.175L时，效率取得最大值，约为92.47%；当翼型最大厚度位置小于0.175L时，轴流泵效率随着最大翼型厚度位置左移而降低；而翼型最大厚度位置大于0.175L时，效率逐渐降低至90%，下降幅度较大。综合2条曲线的变化趋势，当翼型最大厚度位置位于0.175L处时，轴流泵效率达到最大，此时扬程也保持在较高水平，满足设计要求；当翼型最大厚度位置位于0.5L处时，轴流泵扬程和效率出现突增，为局部最大值，相对较优。

为了分析最大翼型厚度位置对轴流泵汽蚀性能的影响，需要对不同模型下的必需汽蚀余量进行预测。本文采用参考文献的计算公式[22]作为必需汽蚀余量的预测公式。根据对叶片汽蚀区域的观察，一般汽蚀发生在叶片背面距离轮毂0.8倍叶片宽度处，且距叶片进口(0.1～0.2)倍叶片长度的位置。因此，在数值计算结果中取出该区域叶片背面的最低压力值作为预测必需汽蚀余量的汽化压力。计算公式如下：

(7)

式中：Pin为叶轮进口总压；Pv为叶轮背面距叶片进口(0.1～0.2)L位置处的最小压力；NPSHre为叶片必需汽蚀余量。

距离轮毂0.8倍叶片宽度(span=0.8)的叶片表面压力分布见图6。在叶轮设计时，近轮缘处厚度较大，使得翼型头部压差过大，容易产生空泡，从而导致局部离散的高压点和低压点。另外，翼型尾部的加厚处理使翼型尾部出现方头，进而在尾部产生局部的压力跳动[22]。根据图6取出(0.1～0.2)L位置处的最小压力，从而计算得到该设计结果的必需汽蚀余量值。

图6 翼型断面压力分布图(span=0.8)Fig.6 Pressure distribution of airfoil section

对于不同最大厚度位置设计结果同样采用上述预测必需汽蚀余量的方法进行计算，得到不同最大翼型厚度位置下汽蚀余量计算值，见图7。从图7中可以看出，轴流泵汽蚀余量曲线随着最大翼型厚度位置的右移而下降，即轴流泵汽蚀性能优化；当最大翼型厚度位置处于(0.1～0.3)L时，汽蚀余量曲线变化平缓，汽蚀性能差异较小；最大翼型厚度位置大于0.3L后，汽蚀余量曲线明显下降，最大翼型厚度靠近翼型尾部时，汽蚀性能较优。

图7 不同最大翼型厚度位置下汽蚀性能曲线Fig.7 Cavitation performance curves of different maximum airfoil thickness positions

综合考虑最大厚度位置的改变对扬程、效率和汽蚀性能的影响，最后发现最大厚度位置选取在(0.175～0.25)L处，轴流泵水力性能较好。

3.2 翼型最大拱度位置

对翼型最大拱度位置的作用规律进行研究时，保持最大厚度位置不变，即为0.25L，改变公式(1)中系数a和b的取值，选取翼型最大拱度位置分别为：0.3L，0.35L，0.4L，0.45L，0.5L，0.55L，0.6L，0.65L，0.7L，0.75L，0.8L，0.85L，共计12种设计方案。

利用CFD数值模拟软件对12种不同的设计方案进行分析，得到了不同翼型最大拱度位置下泵的扬程及效率曲线，见图8。

图8 不同翼型最大拱度位置下扬程及效率曲线Fig.8 Head and efficiency curves at different maximum airfoil camber positions

不同于翼型最大厚度位置下的扬程曲线，翼型最大拱度位置下扬程曲线呈抛物线型分布。随着翼型最大拱度位置不断向尾部移动，轴流泵扬程先增加后减小；翼型最大拱度位置在0.65L时，轴流泵扬程达到最大；当翼型最大拱度位置大于0.65L后，轴流泵扬程急剧降低，因此应避免翼型拱度位置过于偏后的情况。轴流泵效率曲线总体呈抛物线型，当最大拱度位置在0.6L时，效率取得最大值，约为92.54%；当翼型最大拱度位置小于0.6L时，轴流泵效率随着最大拱度位置的增大而升高；随着翼型最大厚度的右移，效率逐渐降低。综合2条曲线的变化趋势，当翼型最大拱度位置位于0.6L时，轴流泵效率最大，此时扬程也较高。

轴流泵必需汽蚀余量曲线见图9。轴流泵汽蚀余量曲线整体呈下降趋势，即汽蚀性能随着最大拱度位置的后移而优化。但与厚度相反的是，当最大翼型厚度位置处于(0.3～0.7)L时，汽蚀曲线下降明显；当最大翼型厚度位置大于0.7L后，汽蚀曲线变化平缓，甚至出现上升趋势。

图9 不同翼型最大拱度位置下汽蚀性能曲线Fig.9 Cavitation performance curves of different maximum airfoil camber positions

综合考虑最大拱度位置的改变对效率、扬程和汽蚀性能的影响，最后发现最大拱度位置选取在(0.6～0.7)L处，轴流泵效率及扬程较高，此时汽蚀性能较好。

3.3 最大翼型厚度与最大拱度位置的共同影响

从上述研究过程可以得出结论，当翼型最大厚度位置处于(0.175～0.25)L时，轴流泵水力性能较优；当翼型最大拱度位置处于(0.6～0.7)L时，轴流泵水力性能较优。但上述的2项研究仅仅从单一变量出发，分别研究2者对轴流泵水力性能的影响。为了进一步确定翼型最大厚度及拱度位置对轴流泵综合性能的影响，分析轴流泵综合性能提高时2者之间相对位置的变化，进一步对轴流泵叶片进行设计分析。

根据“儒可夫斯基”翼型的基本公式，同时改变参数a、b、c、d的大小，选取翼型最大厚度位置为0.15L、0.175L、0.2L、0.225L、0.25L、0.3L，最大拱度位置为0.45L、0.5L、0.55L、0.6L、0.65L、0.7L，对所设计的不同叶片进行模拟分析，得到36组效率、扬程及汽蚀性能计算数据。将36组最大拱度位置、最大厚度位置不同时的效率单独列举，见表3。

表3 最大厚度位置及最大拱度位置不同时效率大小 %Tab.3 Efficiency under different maximum airfoil thickness and camber positions

进而绘制计算结果的分布云图，见图10。

图10 计算结果分布云图Fig.10 Cloud chart of calculation results

根据图10(a)所示，计算扬程随着翼型最大拱度位置的增大而增大，随着翼型最大厚度位置的增大而减小，而翼型最大拱度位置对扬程的影响大于翼型最大厚度位置。从图10(b)可以看出，当翼型最大厚度范围处于(0.15～0.25)L，最大拱度位置处于(0.60～0.65)L时，轴流泵效率达到最大，可以看作为最大效率中心，距离此中心越远，效率越低。从图10(c)上可知，必需汽蚀余量分布基本上是单调的，随着翼型最大拱度位置的增大，必需汽蚀余量越小，汽蚀性能越好，翼型最大厚度位置对必需汽蚀性能的影响不大。当翼型最大厚度位置及最大拱度位置都位于翼型尾部时，汽蚀性能最优。综合图10可以发现，轴流泵叶片设计翼型的最大厚度位置处于(0.15～0.25)L，最大拱度位置处于(0.6～0.65)L时，轴流泵位于最大效率中心，此时扬程较高，满足设计需求，且必需汽蚀余量值小于6 m，汽蚀性能较优。

由此可以得到，在翼型最大厚度位置及最大拱度位置的共同影响下，最大厚度位置及最大拱度位置的取值范围与单因素影响下的取值范围相符合。

目前，国内外学者在设计轴流泵的过程中基本采用的是机翼翼型，参考文献[23]对791翼型厚度进行多目标遗传优化设计，得出翼型最大厚度位置靠近来流方向时，升阻比增大，阻力减小，翼型效果更优。参考文献[1]对翼型最大拱度位置进行研究得到，大流量工况下最大翼型拱度位置越靠近翼型尾缘效率越高。随着最大拱度位置向翼型尾缘偏移，水泵的汽蚀性能有一定的提高。本文采用的是“儒可夫斯基翼型”作为数值计算的基础翼型，计算结果与上述文献存在差别，但趋势是一致的，说明本文的结果是合理的、可靠的。

本文提出，当翼型最大厚度范围处于(0.15～0.25)L，最大拱度位置处于(0.60～0.65)L时，认为翼型设计处于最大效率中心。根据表3可以发现，在最大效率中心内，存在效率最大值，将此点记作为最大效率点，此时翼型最大厚度位置为0.65L，最大拱度位置为0.175L。

为进一步分析2变量对轴流泵综合性能的共同影响，引入参数κ作为研究因子，对κ的取值范围进行讨论。参数κ的物理意义为最大厚度位置与最大拱度位置到最大效率点的距离，公式如下：

(7)

式中：x为翼型最大厚度位置；y为翼型最大拱度位置；a表示最大效率点处最大厚度位置，即为0.65；t表示最大效率点处最大拱度位置，即为0.175。

对36组数据进行处理，得到了参数κ与效率之间的散点图，见图11。

图11 不同κ值下效率散点图Fig.11 Scatter diagram of efficiency at different κ values

从图11可以发现，不同κ值下轴流泵的效率呈多项式分布。当κ值趋近于0时，效率达到最大值；随着κ值的不断增大，效率也逐渐降低。说明最大厚度位置与最大拱度位置距最大效率点越远，轴流泵效率越低。当效率大于92.6%时，认为参数κ的值是期望的，对效率的线性拟合曲线分析，发现此时κ的位置范围为0～0.07。

不同κ值与扬程的散点图见图12。从图12中发现，扬程的拟合曲线呈二项式分布。当κ值取0～0.05时，轴流泵扬程逐渐降低，且变化幅度较小；随着κ的增大，轴流泵扬程大幅度下降，κ取0.2时，扬程已降低至5.36 m。当轴流泵扬程大于5.5 m时，扬程满足设计需求，此时κ值为0～0.17。

图12 不同κ值下扬程散点图Fig.12 Scatter diagram of head at different κ values

不同κ值与汽蚀余量对应的散点图见图13。从图13中看出，随着κ值的增大，轴流泵的必需汽蚀余量先降低后升高。当κ值取为0.05时，必需汽蚀余量较小，轴流泵汽蚀性能最优。当叶片汽蚀余量小于6 m时，轴流泵设计合理，此时参数κ的理想值处于0～0.1。

图13 不同κ值下汽蚀余量散点图Fig.13 Scatter diagram of cavitation performance at different κ values

综上所述，当参数κ取为0～0.07时，轴流泵效率最大，此时扬程满足设计要求，汽蚀性能也能够保持在较好的范围内。

3.4 全工况数值模拟

当翼型最大厚度位置为0.65L，最大拱度位置为0.175L时，轴流泵综合性能最优，此时κ值为0。为了进一步分析此轴流泵模型的水力性能，通过CFD数值模拟的方法，对模型进行全工况数值模拟，见图14。

图14 全工况设计扬程及效率曲线Fig.14 Head and efficiency diagram under full condition design

从扬程曲线可以看出，随着流量的增大，轴流泵扬程呈下降趋势，在设计流量情况下，实际扬程和设计扬程较为符合。从效率曲线来看，轴流泵叶轮模型高效区较宽，轴流泵效率最大值为93.72%，此时流量为300 L/s，偏离设计工况。但在设计工况下，轴流泵效率仍可达到92%，相对较高。在小流量区域，轴流泵效率较高，且变化幅度较小，稳定在90%以上。在大流量区域，效率变化幅度大，呈下降趋势。但在流量距离设计工况较接近的范围内依旧可以保持效率在90%以上，对于维持在大流量工况下的泵站，能够符合其要求。因此，轴流泵叶轮模型的水力效率在不同流量下，能够保持较高的水力性能。

4 结 论

(1)翼型最大厚度位置选取在(0.175～0.25)L处时，轴流泵效率最优，此时扬程与设计值较为符合，必需汽蚀余量满足要求。当最大厚度位置向翼型尾部移动时，汽蚀性能改善较小，但轴流泵效率及扬程下降较快，故翼型最大厚度位置不宜过大。

(2)翼型最大拱度位置选取在(0.6～0.7)L处，轴流泵水力性能较好。当最大厚度位置后移时，汽蚀性能有改善的趋势，可以应用于相关工程领域。

(3)为研究翼型最大厚度位置及最大拱度位置对轴流泵的共同影响，引入参数κ，对36组数据进行数值模拟分析。结果发现，当参数κ取为0～0.07时，轴流泵效率最大，此时扬程满足设计需求，汽蚀性能也能够保持在较好的范围。