基于小波多分辨分析算法下的中美股市联动性研究∗

耿艳秋 佟 良 邹大伟

（绥化学院信息工程学院 绥化 152061）

1 引言

众所周知，股市市场的波动变化叵测，能够掌握国内股市的变化规律及美国股市对中国股市的影响一直都是投资者梦寐以求的事情。目前，关于中美股票市场波动的关联性的技术分析方法也出现了很多，包含有马尔科夫分析法、时间序列分析法、神经网络法等。小波分析（Wavelets Analysis）是20世纪80年代中后期逐渐发展起来的一种新的数学分析方法，它具有丰富的数学理论意义，又具有广泛的工程应用价值。广泛应用在信号处理、图像处理、理论数学、模式识别、语音分析以及其他非线性科学领域。但把小波分析应用在股票市场的数据分析研究中的文章还不多。1995 年，Ramsey J B 等在文献［1］中率先用小波分析预测了标准普尔指数（S&P 500）的未来走势；2002年，Hahn在文献［2］中用小波分析理论研究了土耳其和埃及股市受美国股市波动的影响；1999 年，王哲、王春峰等在文献［3］中给出了小波变换在中国股票市场的数据分析中的应用；2001 年，孟卫东等在文献［4］中用小波理论完成了上证指数奇异信号统计监测，得到了很好的结论；2001 年，候木舟等在文献［5］中研究了基于Matlab 的小波分析在股市技术分析中的应用。基于前人的研究成果，本文将采用小波多分辨分析的方法研究美国股票市场的波动对中国股票市场的影响。

2 小波分析

2.1 小波基函数

小波基函数决定了小波的效率，常用的小波基函数有Haar小波，Morlet小波，Mexico小波[6]等，本文将采用Mexico 草帽小波来分析股市价格的波动趋势。

Mexico小波也称为草帽小波，定义为

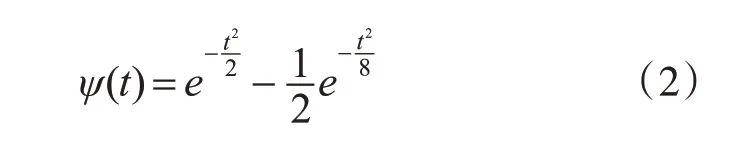
2.2 小波变换

对于非平稳信号而言，我们要求在低频部分具有较好的频率分辨率特性，而在高频部分具有很好的时间分辨率特性，为此，我们引入连续小波变换（CWT）公式如下：

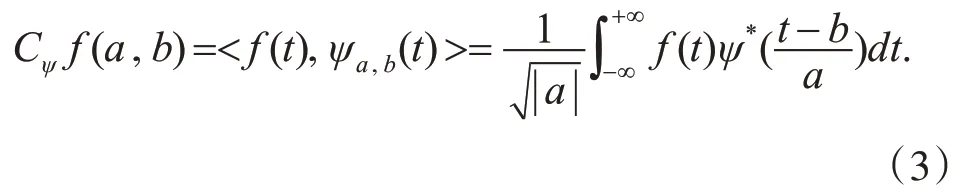
其中，a∈R，a≠0 是尺度因子；b∈R 是时间平移因子；且函数：

是由母小波函数ψ(t)作伸缩、平移得到的。

令式（3）中a=2-m, b=n ⋅2-m, t=kT, m,n,k∈Z, T 为周期，则有离散小波变换（DWT）公式为

2.3 多分辨分析

Mallat 早在1988 年就提出了多分辨分析理论（MRA），并由此提出了现今广泛使用的Mallat快速小波分解和重构算法。多分辨分析就是将各种不同频率组成的混合信号拆分成为各个不同频的子信号，从而，更有利于信号的重构和特征根的提取等［7］。

设{Vj}j∈Z是L2(R)的一个闭子空间序列。如果满足：

1）嵌套性：Vj⊂Vj+1, j∈Z;

从表13的“假设方差相等”行读取数值，t值是8.9590，Sig.(双侧)是双尾T检验的显著性概率0.0001，远小于0.05。可以得出结论：高低侧裂缝严重程度有显著差异，表现为较低一侧的裂缝面积大于较高一侧，究其原因，主要是由于向心力，较低一侧的路面所受的荷载作用力更大，路面某点的荷载作用持续时间相对更长(车辆通过弯道的时间一定，而较低侧的路程更短)，而沥青混合料是一种黏弹性材料，在持续荷载作用下易产生塑性变形，久而久之产生裂缝。

4）伸缩性：f(t)∈Vj⇔f(2t)∈Vj+1, j∈Z;

5）平移不变形：f(t)∈V0⇒f(t-k)∈V0, k∈Z;

6）正交基存在性：存在φ∈V0，使得{φ(t-k),k∈Z}构成V0的标准正交基，则{Vj}j∈Z称为L2(R)的一个多分辨分析（MAR）。

多分辨分析就是用不同分辨率来逐级逼近待分析函数f(t)。由多分辨分析的性质可得

其中，{Vj} 为尺度空间，{Wj} 为小波空间。

假设f∈L2(R)是要处理的实际信号，测得的信号fj是f 在尺度空间{Vj} 中的近似，下面可将fj多分辨表示为

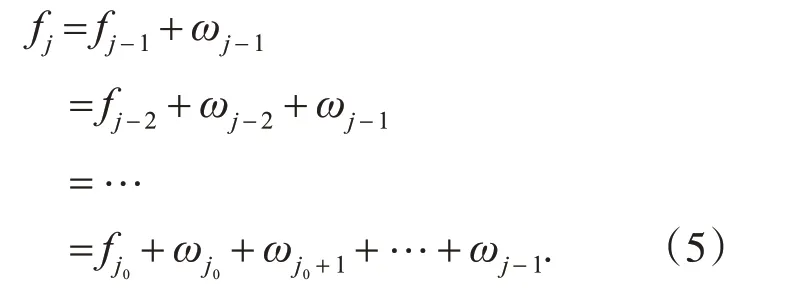
其中，

设函数f(t)∈L2(R) 向不同尺度的小波空间{Wj} 投影后得到的信号是dj(t)∈Wj，则

由式（5）～（8）得

可以证明信号f(t)在分辨率2-l(1≤l≤j)分辨率下的逼近是最好的，其中，式（5）～（8）称为离散正交小波的分解公式，式（9）为离散正交小波的重构公式［8］。多分辨分析有效地对信号低频部分作了分解，这一特点正好满足了对中美股票市场数据间的联动性分析的需要。

3 股市联动性分析

3.1 样本数据

数据来自雅虎财经网，选取日期为2012年7月1 日 至2018 年3 月1 日 为 止，选 取 标 准 普 尔（S&P500）指数、香港恒生指数和上证综指为原始数据分别代表美国和中国内地股市的波动性，首先我们对原始数据进行处理，取各股票的日收盘价的对数收益，即：yt=ln Pt-ln Pt-1，其中Pt是股指的日收盘价；t-1 日为美股交易日；t 日为国内股交易日。 对原始数据进行甄选，得到标准普尔对恒生股指的序列1034 个样本数据；对上证综指股指的序列1104个样本数据［9］。

3.2 样本数据的小波多分辨分析

选用Mexico 小波函数分别对标准普尔（S&P500）指数、香港恒生指数和上证综指的日收盘价的对数收益率的数据进行6 层的正交小波多分辨分析。 将原始信号分解为l=a6+d6+d5+d4+d3+d2+d1。

由式（6）可得到a6的值；由式（7）、（8）可得到d1,d2,…,d6的值。其中φ(t)是Mexico 小波的尺度函数，ψ(t)是Mexico小波函数［10］。这样我们就得到了尺度j(j=1,2,3,4)上的一系列重构数据，如图1～2 所示，d1,d2,…,d6分别表示尺度21,22,…,26上变化的数据。

图1 上证-标准普尔500指数

由图1、图2可以看出，美国股市与国内股市的高频d1具有很好的相似性［11］。小波多频率分析方法可以提取原始数据中的高频部分，从而能够有效分析中美股市间的联动性关系。

图2 恒生-标准普尔500指数

表1 各频率占比（%）

表1 表明，高频成分所占的比例远远大于低频部分，其中d1大约占比50%，因此从表中可看出：1）股市的日收益率受短期因素的影响严重，具有不可预测性；2）香港的股市短期波动性最大，上海股市次之，而美国股市短期波动与前两者比较相对要小［12～13］。

为了研究美国股市对国内股市波动性的影响，下面对这三只股票经多分辨分析分解后不同尺度上的联动性进行线性回归分析[14]。 数据样本量n=1034，置信水平α=0.1 时与样本量n=1104，置信水平α=0.01时分别分析如表2。

表2 相关系数表

4 结语

随着中国股市国际化步伐的日益加快，中国股票市场与国际股票市场日益融合；全球股市股指间的聚集效应更为显著，股指间差距缩小，联动性增强，这就是全球经济“一体化”发展的必然结果［15］。本文通过小波多分辨分析法这一有效工具对上证指数、香港恒生指数和S&P500 标准普尔指数的日对数收益率时间序列进行了多尺度的复杂性分析，证明了美国股市对香港股市波动性影响很大，而对上海股市波动性影响很小。