一阶旋转倒立摆输出反馈控制
于树友,褚建新,王银敏
(1. 吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130022;2. 吉林大学 控制科学与工程系,吉林 长春 130012)
倒立摆系统具有多变量、强耦合、非线性且不稳定等特性[1],所有重心在上支点在下的问题都可以用倒立摆问题来概括。科研人员通过对倒立摆的控制检验自己的控制算法,直观地表现稳定性、可控性等关键问题。倒立摆有着深刻的工程背景,相关理论成果已经在直升飞机、火箭发射、人造卫星、机器人等方面得到了广泛应用[2-3]。
按运动方式分类,倒立摆主要有两类控制问题,一是使摆杆保持在竖直倒立位置的平衡控制,二是摆杆从静止下垂状态到竖直倒立方位所进行的起摆控制[4]。在进行平衡控制时,采用了基于观测器的输出反馈控制策略,分别采用极点配置法和最优控制策略设计平衡控制器。在本文中,针对摆杆及旋转臂角速度不可测量问题,研究了一阶旋转倒立摆在不稳定平衡点处的状态观测器设计问题,分别设计了降维观测器和高通滤波器对不可测状态进行观测。在进行起摆控制时,采用了能量控制策略。用Matlab/Simulink 工具完成了仿真环节,并在实验环节成功完成了对倒立摆的平衡控制和起摆控制,验证了控制器的有效性。该方法应用于自动控制相关课程的实验教学,强化了学生对控制系统建模、控制器设计等理论知识的理解。
1 一阶旋转倒立摆的控制问题
一阶旋转倒立摆的旋转臂和摆杆可以简化成两个均匀的质量杆,其模型结构与相应的实物如图1 所示,一阶旋转倒立摆的参数及物理意义见表1。
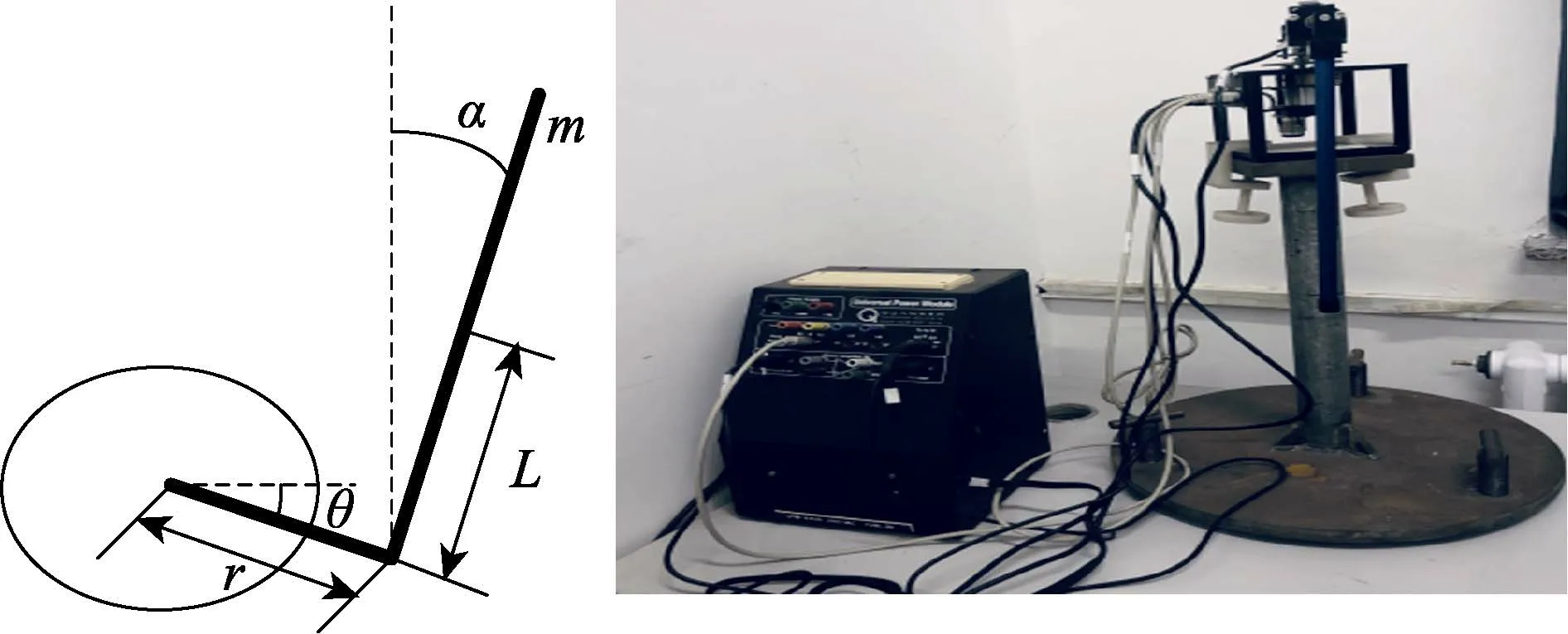
图1 旋转倒立摆系统示意图

表1 系统物理参数表
由图1 可知,系统的动能包括:旋转臂转动的动能,摆杆摆动的动能,摆杆质心在水平方向和竖直方向的动能。定义零势能面为旋转臂转动的平面,则系统的动能和势能可分别记为T和V,则:
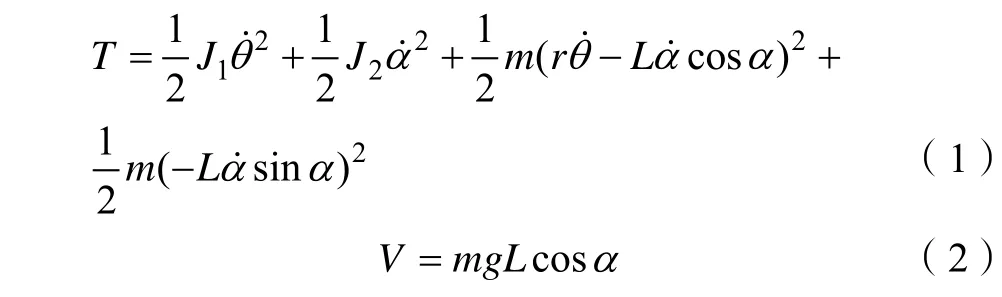
动能与势能的差记为H[5],则:
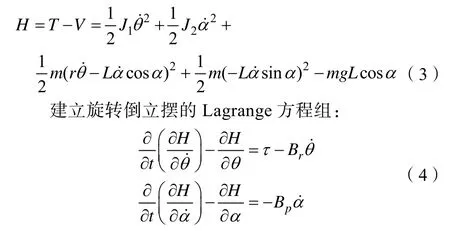
其中τ代表直流伺服电机输出组转矩,且有:
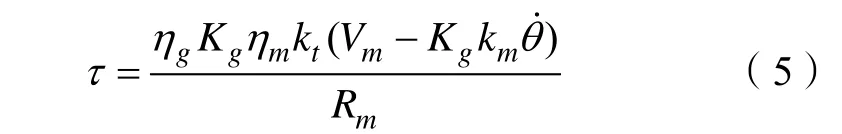
计算式(4)中的各个分量[6],并在平衡位置附近(α≤ 0.1745 rad )进行线性化,得到如下线性方程组
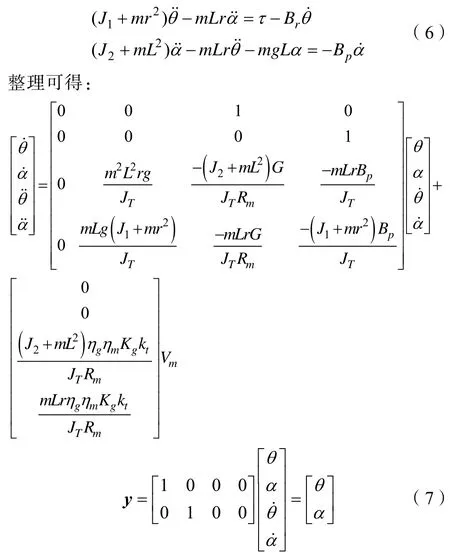
其中,JT=+J1mL2+J2mr2,G=+。将相关参数值代入式(7),得到一阶旋转倒立摆系统的线性化模型:

系统是以旋转臂角位移、摆杆角位移、旋转臂角速度和摆杆角速度为状态变量,以直流电机输入电压为输入的4 阶线性系统。系统满足可控性的充分必要条件rank[B AB A2B A3B] =4,系统满足可观性的充分必要条件rank[C CA CA2CA3]T=4,所以系统是可控、可观的。其中,A为状态矩阵,表示系统内部变量之间的联系;B为输入矩阵,表示各个输入变量如何控制状态变量;C为输出矩阵,表示输出如何反应状态变量。
2 观测器设计
由于倒立摆的摆杆和旋转臂的角速度(θ˙和α˙)无法直接测得,需要利用状态观测器对系统状态进行观测[7]。本节讨论状态观测器的设计方法,并对其观测效果进行对比和分析。
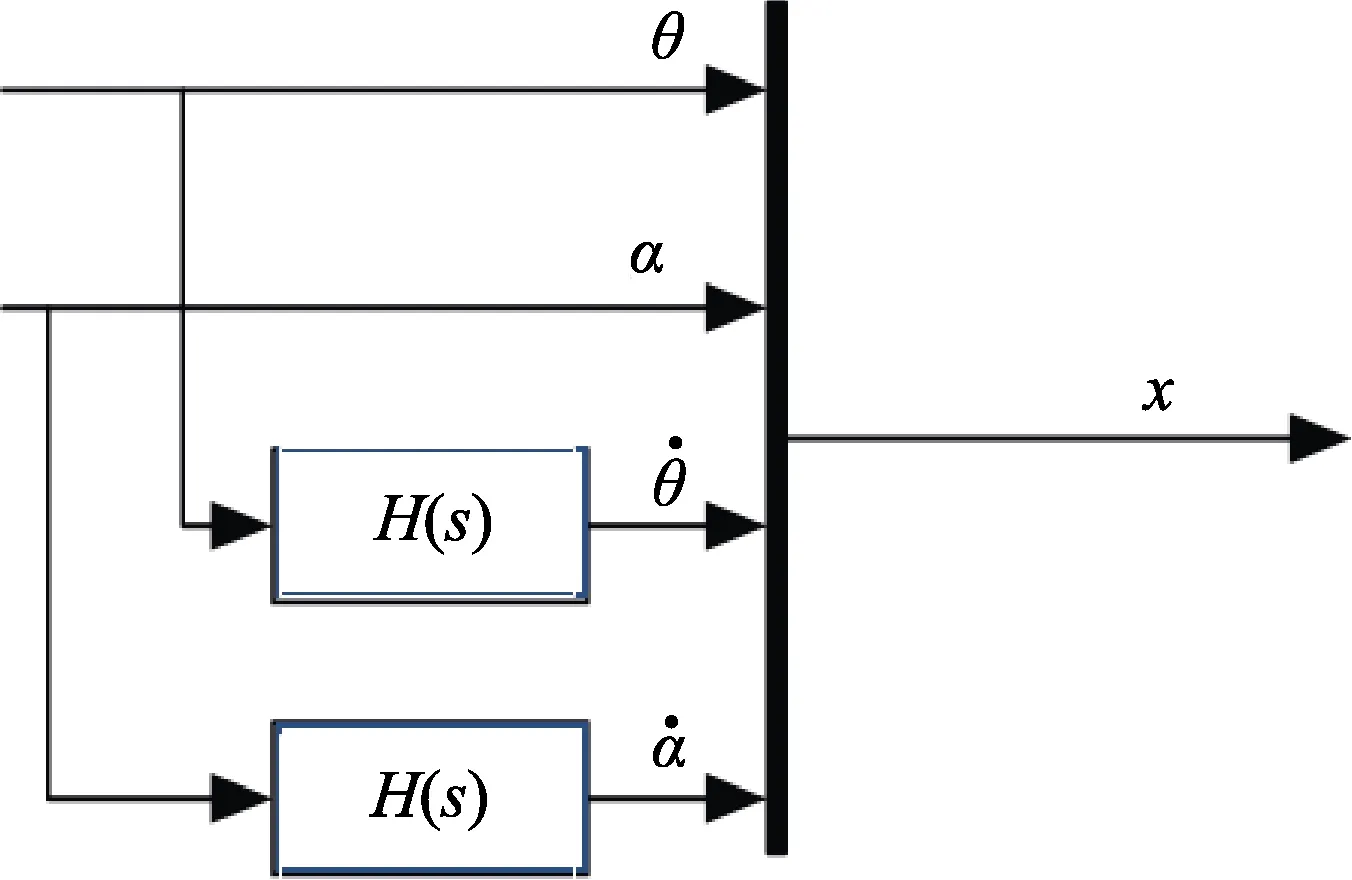
图2 高通滤波器状态观测结构图
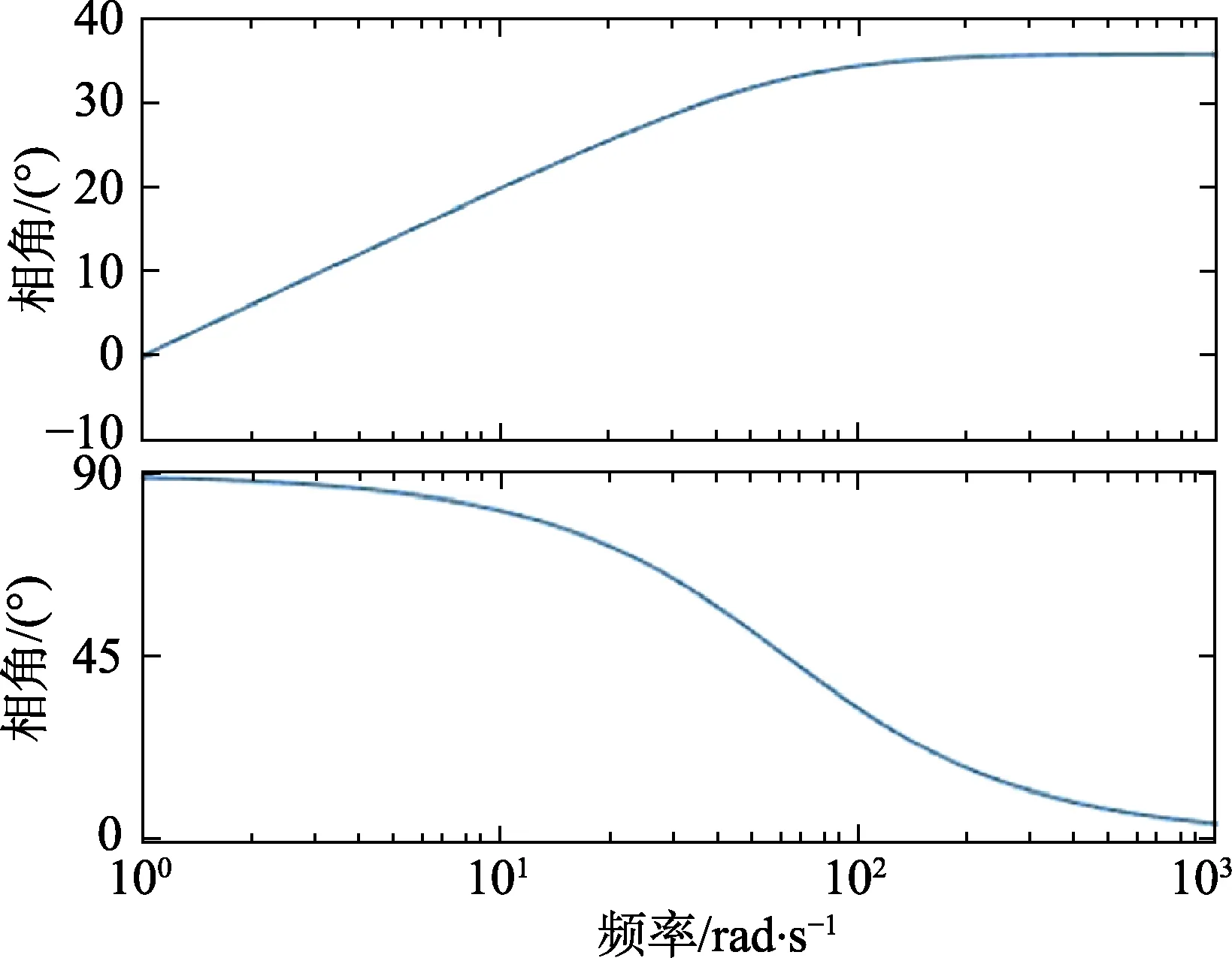
图3 高通滤波器幅相曲线特性
2.1 函数观测器
在设计降维函数观测器时,首先给出了观测器的结构如下:
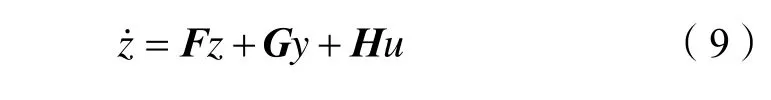
其中,z为待观测的状态,F、G、H是构成降维状态观测器的待求矩阵。F阵的选取与观测器的期望极点有关,G阵是一个任选的非奇异矩阵,H阵的值则需要求解一个Sylvester 方程。从观测器综合原则出发,取观测器的特征值负实部为A-KB特征值的负实部的2~3 倍[8]。以平衡控制器中的极点配置法为例,并经过多次实验,最终选取观测器极点为 -10.5±10.5j。列出期望的特征方程(λ为特征根):
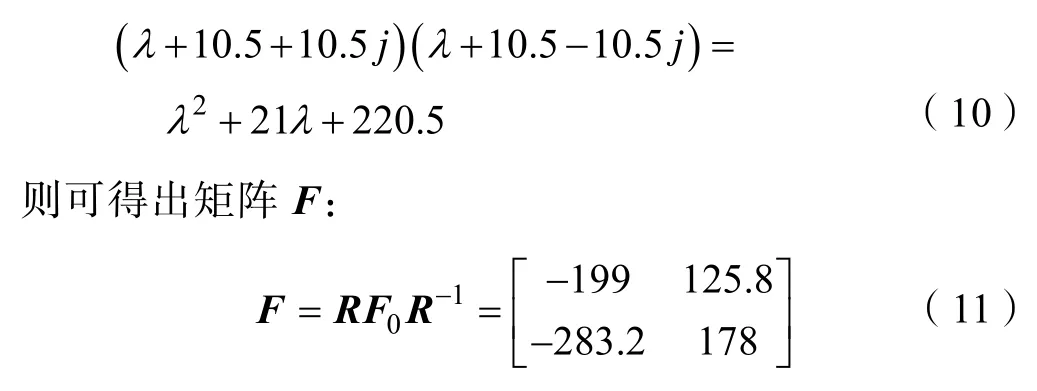
任取一个常矩阵G,使得 [F,G] 满足完全可控条件。
求解Sylvester 方程TA-FT=GC,得:
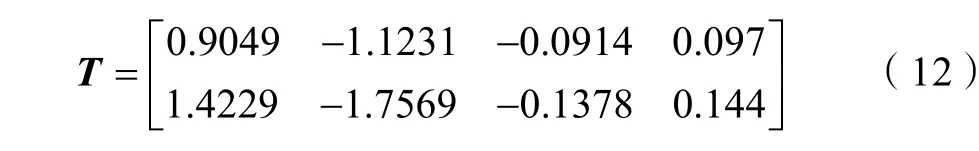
记P=[CT]T,rank(P) = 4表明P为非奇异阵。若P为奇异阵,则需重新选取R及G阵。
计算矩阵H:
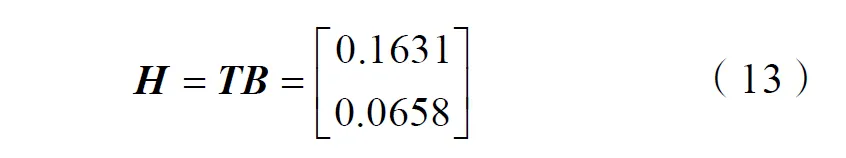
则函数观测器的实现为Q=[Q1,Q2]:

2.2 高通滤波器
一阶倒立摆系统中两个不能直接测得的状态变量θ˙和α˙分别是可测变量θ和α的一阶微分。由于微分环节不稳定,故采用一阶高通滤波器来近似一阶微分环节。选取如下形式的一阶高通滤波器:
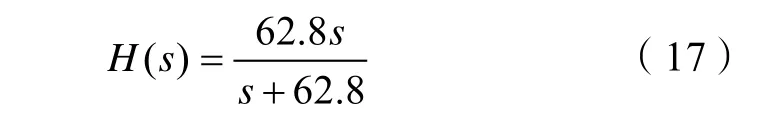
图2 为高通滤波器状态观测结构图,图3 为高通滤波器幅相曲线特性。从图3 可以看出,在频率ω=0附近一阶高通滤波器H(s) 可以很好地近似一阶微分环节。
2.3 观测效果分析
为了对观测效果进行比较,现假设旋转臂角速度、摆杆角速度都可测,通过Simulink 仿真输出两个状态变量的大小,再使加入观测器观测到的状态变量与之比较。为了使仿真结果更具有说明性,采用平衡控制的仿真过程来产生一个动态环境,取极点配置法设计的状态反馈矩阵,仿真结果如图4、图5 所示。
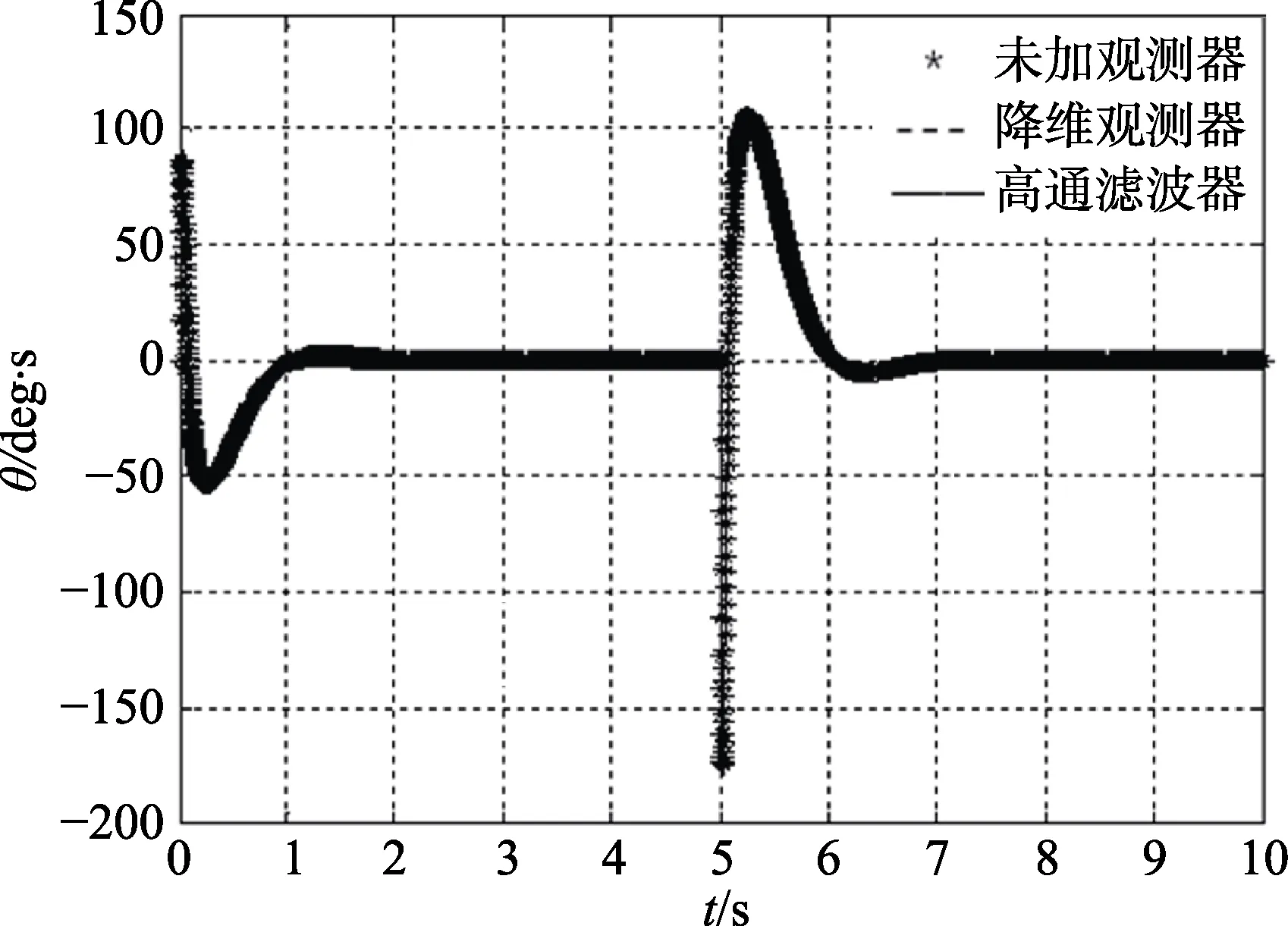
图4 观测结果图
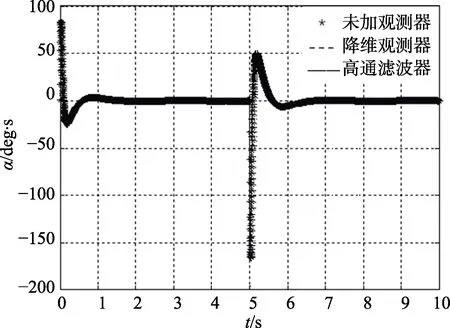
图5 观测结果图
从仿真结果可以看出,降维状态观测器的观测效果很好。考虑到针对极点配置法以及LQR 法设计状态反馈控制器时,观测器的形式是不同的,同时由于实验要反复多次进行,状态反馈矩阵K经常会发生变化,所以采用降维状态观测器显然会大大增加实验负担。采用高通滤波器进行状态观测时,观测曲线比较平滑,且高通滤波器的结构不会随闭环系统极点的变化而变化,因此在接下来的仿真及实验过程中,都将采用高通滤波器来进行状态观测。
3 平衡控制器设计
研究一阶旋转倒立摆的平衡控制问题。采用了基于观测器的输出反馈控制策略,考虑到线性系统的分离原理,状态观测器和状态反馈控制器可以独立设计。本节分别用极点配置和LQR 两种控制方法实现倒立摆的平衡控制。
3.1 极点配置控制器设计
由于系统参数矩阵(A,B)可控,可以寻找合适的状态反馈矩阵K,使系统闭环极点达到期望值。我们期望闭环系统的超调量和调节时间为:

假设该闭环系统极点由一对共轭闭环主导极点和两个非主导极点构成。系统的动态特性主要由共轭闭环主导极点决定,与二阶欠阻尼系统具有相似的动态特性,则二阶欠阻尼系统中超调量和调节时间为:
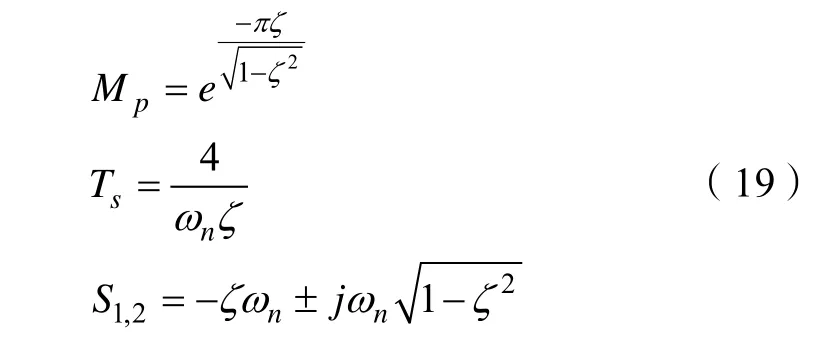
其中,ζ为欠阻尼二阶系统的阻尼系数,nω为自然角频率。
根据式(18)和式(19)可以得到系统的一对闭环主导极点:
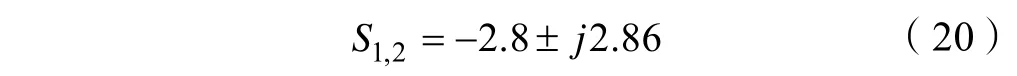
另外两个非主导极点应满足[9]:
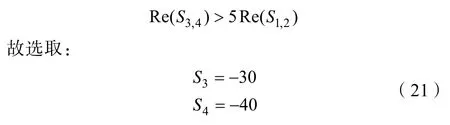
由式(20)和式(21)可以确定系统期望的特征方程为:
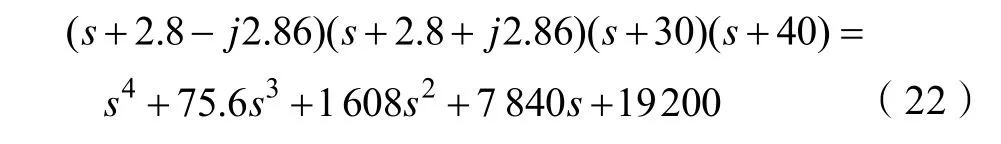
相应得到状态反馈矩阵为:
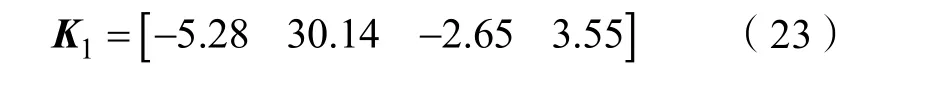
3.2 LQR 控制器设计
采用LQR 法设计的闭环控制系统,其控制性能主要由加权矩阵Q和R决定,加权矩阵Q和R的选择反映能耗和误差的折中。本文取R阵为1。Q阵的对角阵qi,i= 1,2,3,4表示设计者对状态变量xi的关注程度,越重视某个状态变量,越希望其误差分量尽可能小,Q的对角元素相应的qi就要取得越大[10]。在一阶旋转倒立摆的控制过程中,主要目标就是使摆杆倒置稳定,也就是说对状态变量α的重视程度最高,其对应的值也应该最大。在本文中取:
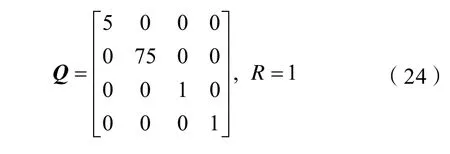
计算得出最优反馈矩阵为:
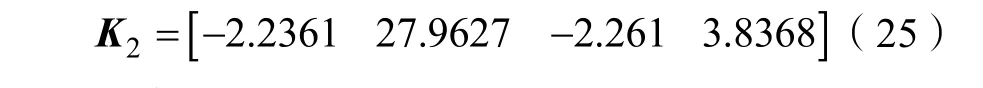
3.3 控制效果及分析
极点配置和LQR 两种控制算法作用下的旋转臂角位移θ、摆杆角位移α以及直流电机输出电压mV的仿真结果分别如图6、图7 和图8 所示。
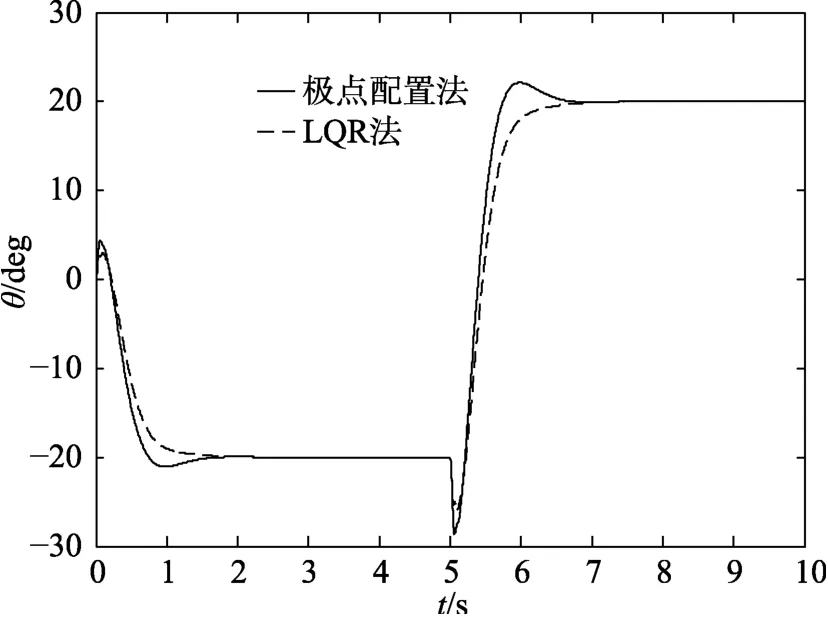
图6 θ 的仿真结果图
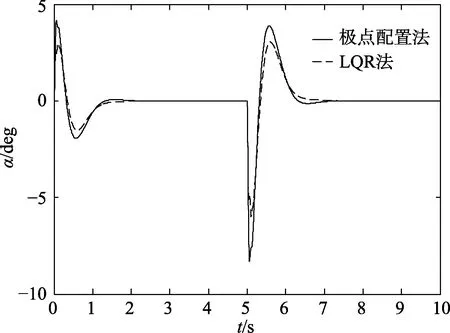
图7 α 的仿真结果图
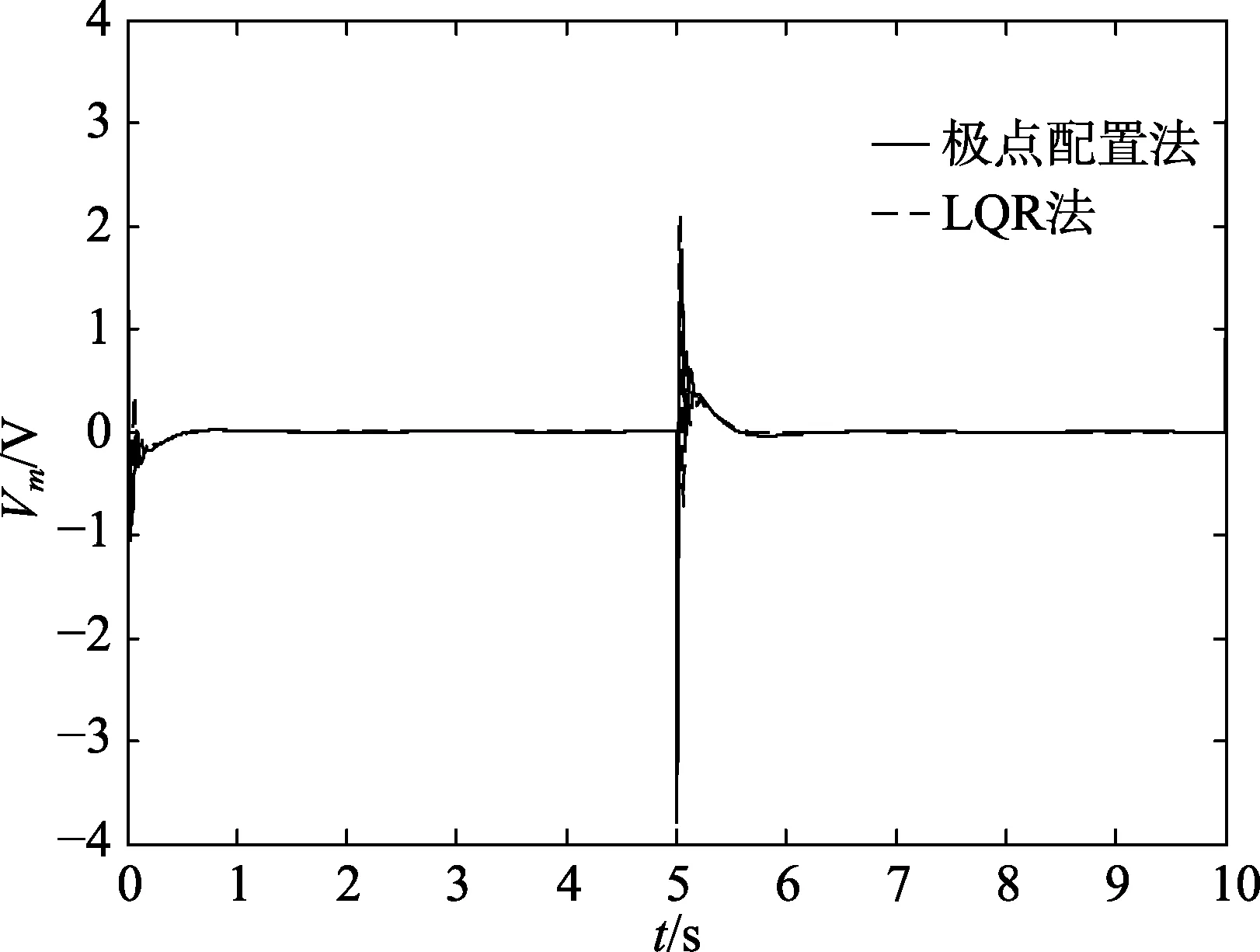
图8 Vm 的仿真结果图
由图6 可以看出,LQR 法设计的控制器控制系统,在θ值突变时其旋转臂旋转的幅度较极点配置法小,但是扰动影响持续的时间更长一些。从图7 和图8 可见,将LQR 法设计的控制器运用到倒立摆的控制时,其摆杆角位移波动的幅度和直流电机输出电压波动的幅度更小,即损耗的能量更少。
为了验证两个平衡控制器的实用性,必须进行具体的平衡控制实验。本文的实验借助QuaRC 软件,在Matlab/Simulink 中搭建了控制模型来实现实时控制。在旋转臂上加入幅值为20、周期为10 的方波信号进行扰动测试,可以验证控制算法的抗干扰能力,实验结果如图9、图10、图11 所示。
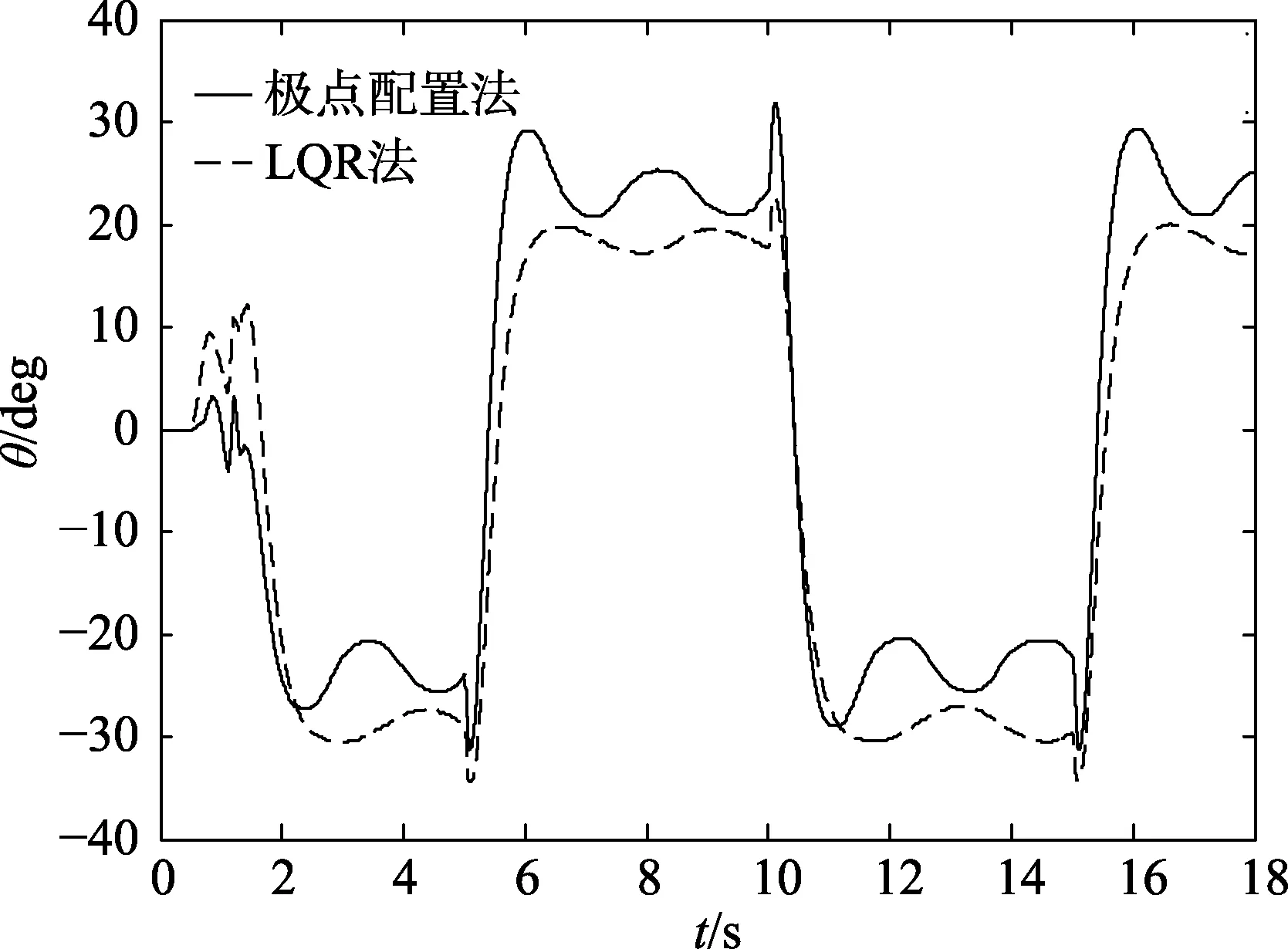
图9 θ 对比图
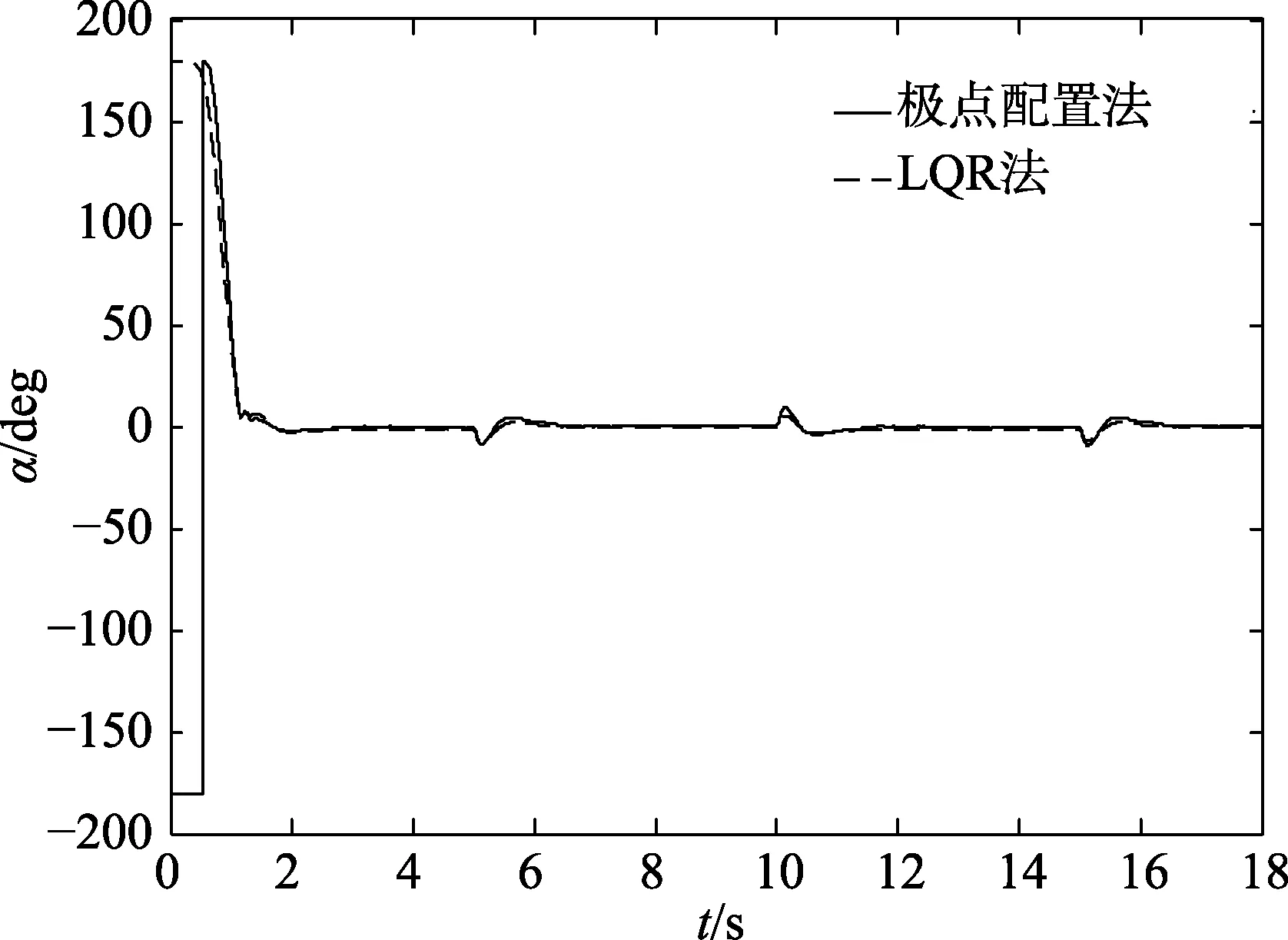
图10 α 对比图
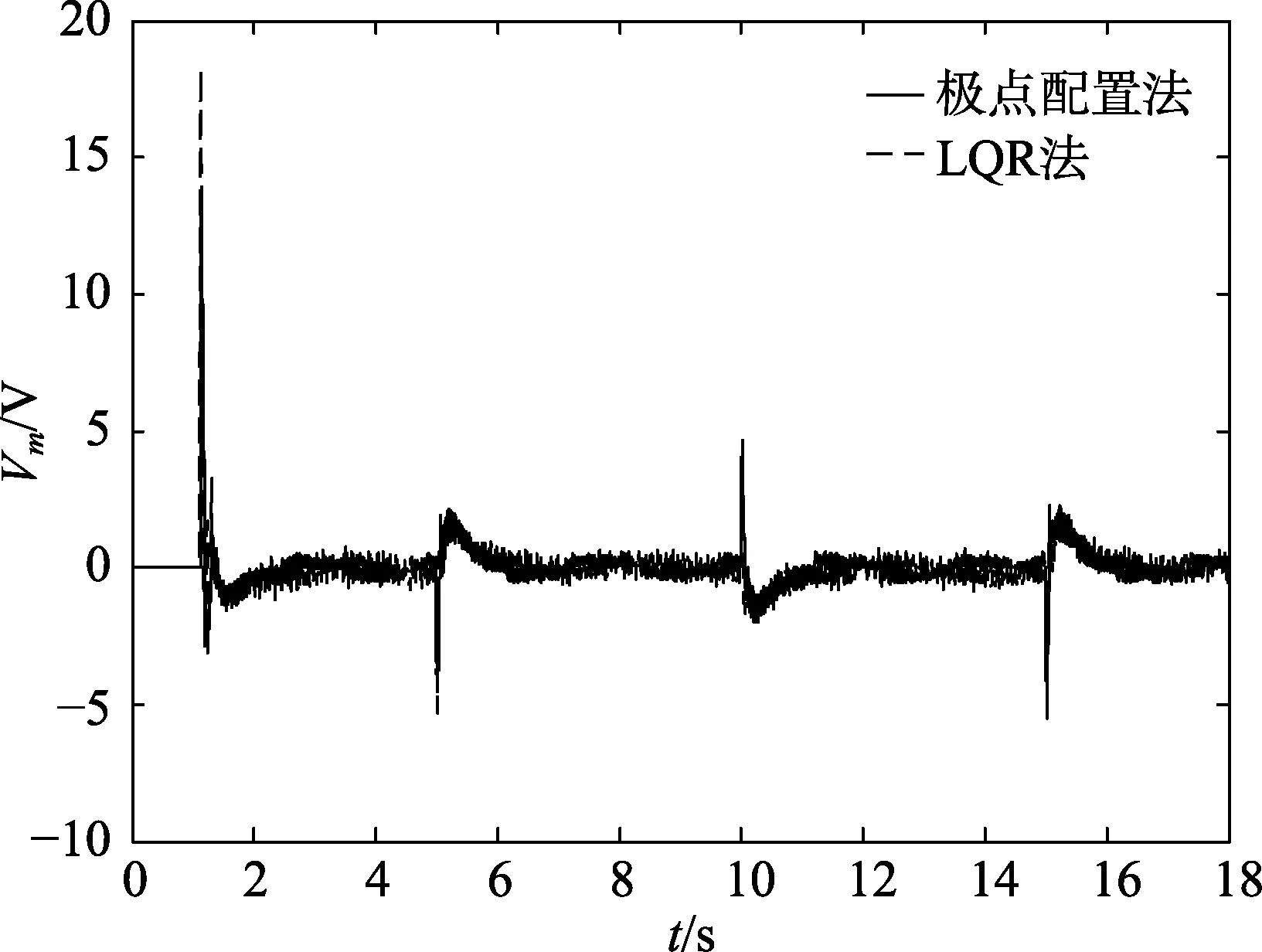
图11 Vm 对比图
从图9 可以看出,当旋转臂受到方波信号干扰时,采用LQR 法控制的倒立摆的旋转臂不会出现转动特别剧烈的情况。从图10 和图11 可以看出,在受到干扰时,采用LQR 法设计的控制器使倒立摆的摆杆摆动幅度更小,电机输出能量也更少,LQR 法的优越性非常明显,这样的实验结果与上述仿真结果一致。
4 起摆控制器设计
起摆控制是指摆杆从常见的下垂状态运动到竖直向上状态的过程,本节采用能量控制策略讨论摆杆的起摆控制问题[11]。以摆杆处于自然下垂状态时质心所在的位置为零势能点。
记E为摆杆的机械能,则:
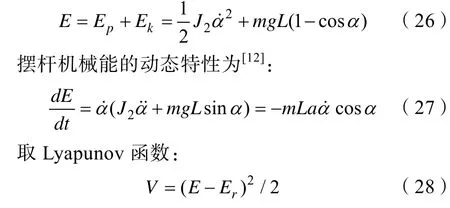
其中Er为摆杆在竖直向上位置的势能。
为使系统渐近稳定,则取轴加速度:
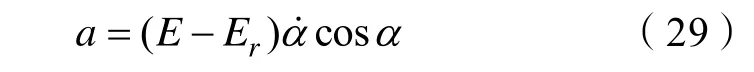
在实际的倒立摆系统中,一切动作的实现都依赖电机的输出,轴加速度a的改变也不例外。在旋转倒立摆系统中有:

由电机输出转矩与电压的关系,可以得出:
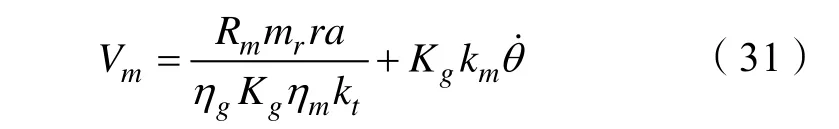
实验结果及分析如图12、图13、图14 所示。其中,θ和α分别为旋转臂角位移和摆杆角位移。
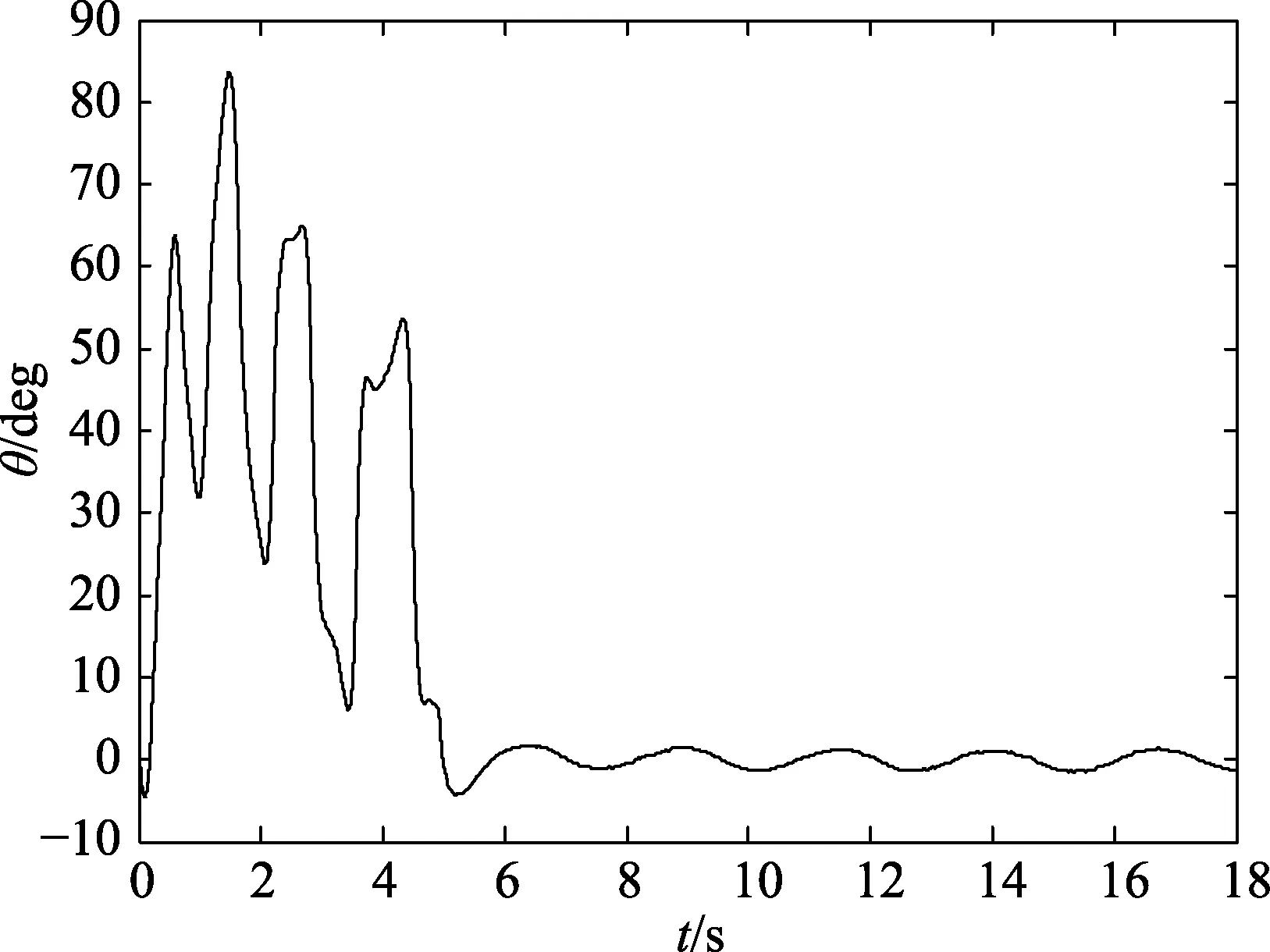
图12 θ 变化图
由实验结果可以看出,系统在7 s 左右即可达到稳定状态,控制效果较好,实验成功。
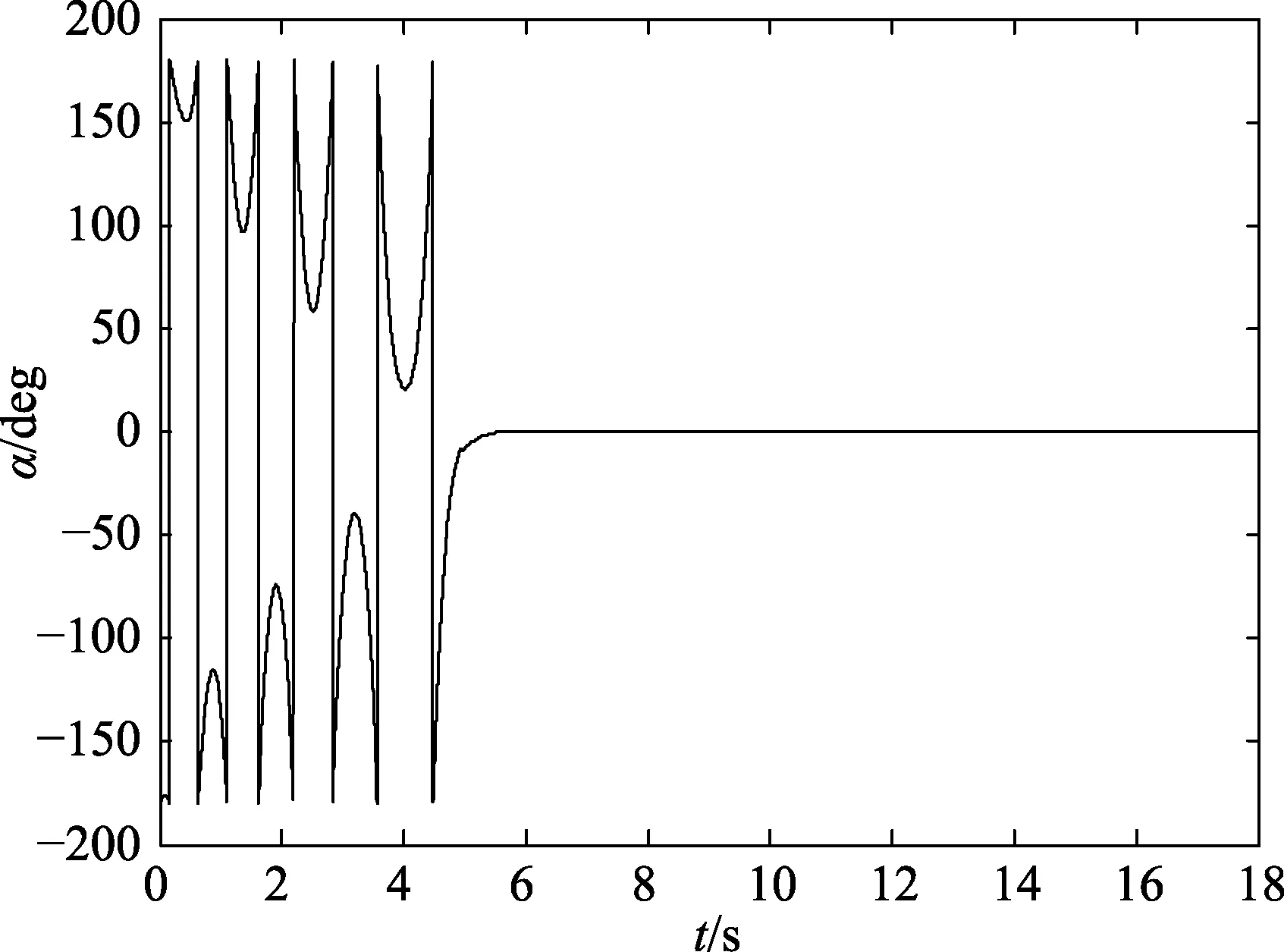
图13 α 变化图
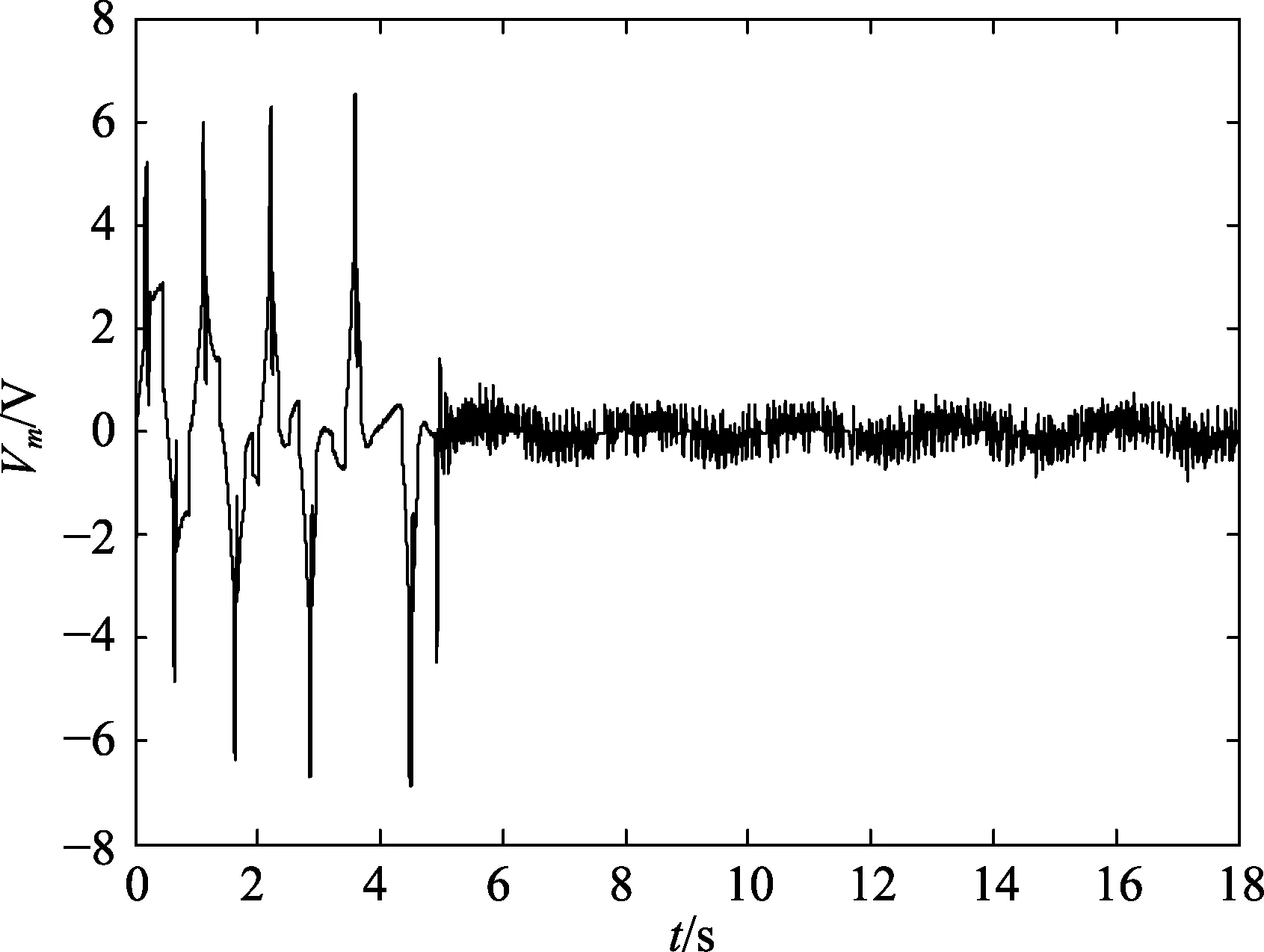
图14 Vm 变化图
5 结语
一阶旋转倒立摆要通过对旋转臂的控制来实现对摆杆的控制,使摆杆最终能够处于倒置稳定状态。分别用极点配置法以及LQR 法设计倒立摆的平衡控制器。仿真及实验对比结果表明,用LQR 法设计的控制器控制效果更好。由于旋转臂角速度和摆杆角速度不可测量,采用高通滤波器观测不可测量的状态。采用能量控制策略设计倒立摆的起摆控制器,并通过实验验证了控制器的有效性。通过实验还验证了一阶旋转倒立摆系统模型及所设计的控制器的有效性,也进一步证明了该教学平台操作简单、稳定可靠。将该实验应用于本科教学,达到了以下教学目的:
(1)建立系统数学模型,掌握控制器的设计过程,为学生今后分析类似的控制系统、设计算法提供思路;
(2)熟悉Matlab 编程环境,掌握Matlab 仿真实验设计与分析;
(3)掌握一阶旋转倒立摆的工作原理和应用,通过实验直观展示了系统工作过程。
该一阶旋转倒立摆实验教学在自动控制相关课程中的应用,将大大提高教学质量和效果。以往的实验内容多是在计算机上完成的,需要学生自己亲自动手的该实验将大大提高学生的热情与积极性。该实验形式是值得肯定的,应多提供类似机会,发挥学生的主观能动性,使学生变被动学习为主动学习,增大科研兴趣,提升实践能力,培养团队精神,为进入工作岗位打下坚实基础。

