基于田口法的熔融沉积制造表面粗糙度实验研究

赵鹏程，李 智，商 正，王进峰

（1. 华北电力大学 教务处，河北 保定 071003；2. 华北电力大学 机械工程系，河北 保定 071003）

3D 打印技术是智能制造9 大核心技术之一[1]，“新工科”建设要求将3D 打印等新技术引入到本科教学工作中。限于成本等原因，在高校实训中应用较为广泛的是基于熔融沉积制造（FDM）工艺的3D 打印技术，其打印材料为PLA 或ABS 丝材。通过热喷头加热令丝材融化，在送进机构的作用下，融化的丝材通过喷头挤压到成型工作台上，层层叠加逐渐成型。由于阶梯效应，零件往往存在表面粗糙度高、表面质量差等问题[2]。FDM 工艺成型过程中，层厚、打印速度等因素的变化，都会对成型件的表面质量造成影响[3-4]。

为了提高FDM 工艺零件的成型精度，科研工作者从工艺原理、分层算法、路径规划、送丝机构等方面进行了广泛研究[5-8]。而成型过程中的参数设计对成型精度的影响是最直接的，例如层厚、打印速度、温度等。韩江等人分析了尺寸误差和表面精度误差的产生机理，通过设计层厚、打印速度、温度3 因素的正交实验，验证了降低表面精度误差方法的有效性[9]。吕福顺分别以ABS 和PLA 两种材料的圆筒为研究对象，研究了层厚对不同直径的圆筒件成型精度的影响[10]。刘莉琳以尺寸误差和打印时间为优化目标，以层厚、打印速度、温度为优化参数，进行了实验研究[11]。

表面粗糙度是衡量FDM 工艺成型精度的主要指标。为了探究温度、层厚和打印速度对快速成型件表面粗糙度的影响，本研究设计了3 因素3 水平的正交实验。通过表面粗糙度仪测量打印件表面粗糙度，并进行信噪比计算和方差分析，来确定影响表面粗糙度的敏感性因素。

1 实验准备及实验方案

本次实验采用的FDM 3D 打印机如图1 所示。耗材为直径0.7 mm 的黄色PLA 丝状材料。

图1 FDM 3D 打印机

用Pro/E 建好模型，并导入Cura 软件中，模型如图2 所示。

图2 打印的模型

实验为采用3 因素3 水平的正交实验，各因素水平如表1 所示，正交实验表如表2 所示[12]。

表1 因素水平表

表2 正交实验表

2 基于田口法的表面粗糙度分析

使用探针式表面粗糙度仪测量打印件侧面的表面粗糙度，如图3 所示。

图3 粗糙度测量

为了保证测量的准确性，使用该粗糙度仪对被测对象的4 个侧面各测1 次，测得的数据如表3 所示。为了确定影响其表面粗糙度的敏感性因素，利用田口法对表面粗糙度Ra进行信噪比计算和方差分析。信噪比（S/N）通过公式（1）计算，计算结果如表3 所示。

式中，η为信噪比，yi为表面粗糙度，n= 4

表3 表面粗糙度及信噪比

对于FDM 3D 打印而言，要求表面粗糙度越小越好，因此对表面粗糙度的优化按照基于望小目标的参数优化方法进行。首先，计算各因素在各水平的信噪比的和值和平均值，如表4 所示。

表4 各因素水平信噪比和值T 及均值Q

然后计算实验总波动及各因素波动方差Si，实验总波动ST：

其中，r为各因素各水平的实验次数，本例r= 3。各因素方差分析如表5 所示。

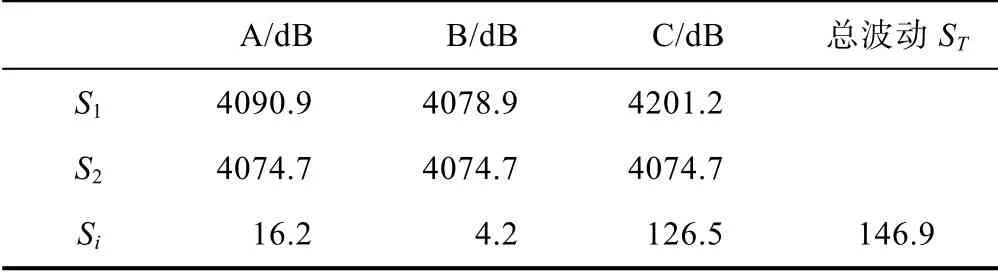
表5 各因素方差分析

从表5 各因素方差的大小可以明确判断，层厚对于表面粗糙度的影响最大，温度次之，打印速度最小。

根据田口法的原理，要求每个因素输出的信噪比越大越好。根据每个因素的平均值，选取最大者作为该因素的最优参数，据此确定最佳参数组合为A2B2C1，即温度选择220°、打印速度选择60 mm/s、层厚选择0.08 mm。最佳参数组合产生的表面粗糙度Rae和信噪比Se可通过式（6）、式（7）计算。

式中，分别表示因素A 在第二水平的平均值、因素B 在第二水平的平均值和因素C 在第一水平的平均值，为表面粗糙度平均值（见表3）。

因此，通过田口法可估算出在温度为220 ℃、打印速度为60 mm/s、层厚为0.8 mm 时，能够获得最小的表面粗糙度为4.95 μm。

3 结语

（1）采用不同打印参数组合，打印件的表面粗糙度差别较大。各参数对打印件表面粗糙度的影响程度从小到大依次为层高、温度、打印速度。

（2）田口法能够用于FDM 3D 打印件最优参数组合的预测。

（3）限于实验条件，本次研究没有考虑热喷头丝材挤出速度的影响，这将在今后的工作中进一步考虑。