基于动态电路模型的超导电动悬浮系统特性分析

刘子琦

1 绪论

电动悬浮因其速度達到一定时自动起浮且不需要额外控制的优点而被广泛应用于高速磁悬浮推进领域，如美国的Magplane磁悬浮列车[1-3]、Holloman磁悬浮火箭橇[4-7]和日本的山梨线磁悬浮列车[8-10]。Magplane磁悬浮列车的悬浮导向系统由车载永磁体和轨道铝板组成，因铝板涡流损耗大和浮重比低等缺点仍停留在概念设计阶段。Holloman火箭橇的悬浮导向系统由橇载低温超导体和轨道铜板组成，2013年最大试验速度可达Ma0.8，但因其浮阻比低，并不适用在大质量悬浮推进场合。日本山梨线磁悬浮列车的悬浮导向系统由车载低温超导磁体和轨道零磁通线圈（8字线圈）组成，超导直线同步电机实现推进，最高试验速度达603km/h。因此，日本超导电动悬浮系统非常适用于大质量高速度悬浮推进的应用场景，如高速飞行列车和磁悬浮航天助推发射。

关于日本超导电动悬浮系统国内外学者均有相关研究[11]-[13]。本文在前人研究基础上，对感应金属板上的超导运动进行仿真模拟，运用得到的数据分析超导模型的特性。

2 超导电动悬浮数学模型

图1由轨道上的若干个8字线圈和车载超导线圈组成。每个8字线圈由上下两个完全相同的回路构成（电流流向相反），上下回路的电阻与电感大小相等。运动的超导线圈在8字线圈中产生感应电流，二者相互作用从而产生悬浮力（fx）、导向（fz）和磁阻力（fy方向）。

该过程可用以下物理方程式进行描述：

其中，H为磁场强度，μ为材质磁导率，并且默认在整个过程中保持不变。ρ为电阻率，并且在整个过程中超导材料的电阻率默认为0。由此可得出：

其中V为超导线圈的体积，B为磁通密度，J为线圈中的电流密度。

3 超导电动悬浮特性分析

3.1  分析对象

以日本超导磁浮试验线MLU002型号列车[13]的悬浮系统为研究对象，表1列出了超导线圈和8字线圈回路的相关参数。单个超导磁体由4个超导线圈组成。

3.2  特性分析

（1） 速度影响

图2（a）和图2（b）分别为超导磁体所受的悬浮力、导向力和磁阻力以及浮阻比和浮导比随列车运行速度的变化曲线，其中8字线圈竖向与横向间隙分别为18cm和15cm，超导线圈悬浮高度3cm。其中，悬浮高度和8字线圈竖向与横向间隙定义如图1所示。由图2（a）知，悬浮力和导向力均随速度的增大而增大，且呈现饱和趋势，而磁阻力随速度的增大而减小。由图2（b）知，浮阻比随速度的增大而增大，且基本呈线性增大趋势，1000km/h时可达300以上;浮导比也在随速度的增大而增大，逐渐呈现饱和趋势，其中1000km/h时为4.63。

（2） 8字线圈横向间隙的影响

图3为超导磁体所受的悬浮力在8字线圈横向间隙为12cm、15cm、18cm、21cm和24cm下的波动曲线，其中悬浮高度为3cm，超导磁体速度为1000km/h。由图3可知，横向气隙不仅影响悬浮力的大小，而且影响悬浮力的波动频率与波动幅度。

由图3和表2可得如下结论：1） 无论横向气隙多大，悬浮力均具有波动特性，这是超导电动悬浮系统自身固有的特性;2） 悬浮力波动的距离周期，即波长，等于8字线圈极距;3） 8字线圈极距越短波动频率越大;4） 悬浮力的平均值随着横向间隙的增大而减小;5）悬浮力的波动幅度在横向间隙为15cm时最小为1.51%，此时8字线圈的极距为0.7m，是超导线圈极距2.1m的三分之一。通过检验其他工况下的计算结果，均得出当8字线圈的极距为超导线圈极距的三分之一时，悬浮力的波动幅度最小，悬浮力稳定性最优的结论。

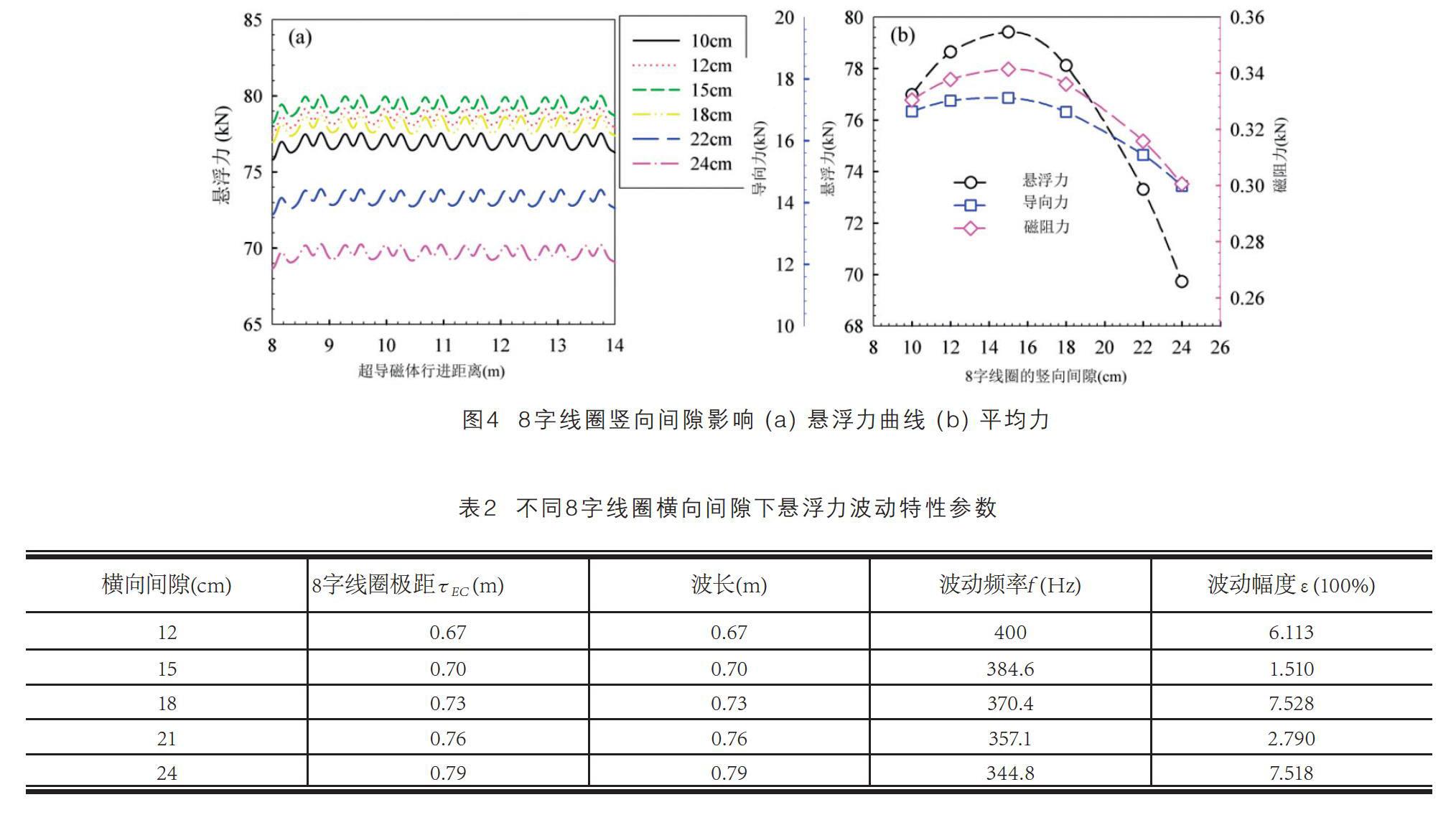
（3） 8字线圈竖向间隙的影响

图4（a）为超导磁体所受的悬浮力在8字线圈竖向间隙为10cm、12cm、15cm、18cm、22cm和24cm下的波动曲线，其中8字线圈极距为0.7m，超导磁体的悬浮高度和速度分别为3cm和1000km/h。由图4（a）知，竖向间隙不会影响悬浮力波动的波长、频率与波动幅度，会影响悬浮力平均值的大小。图4（b）为悬浮力、导向力与磁阻力的平均值随竖向间隙的变化曲线，知：平均力随竖向间隙的增大呈先增大后减小的趋势，在15cm的竖向间隙时平均力最大。

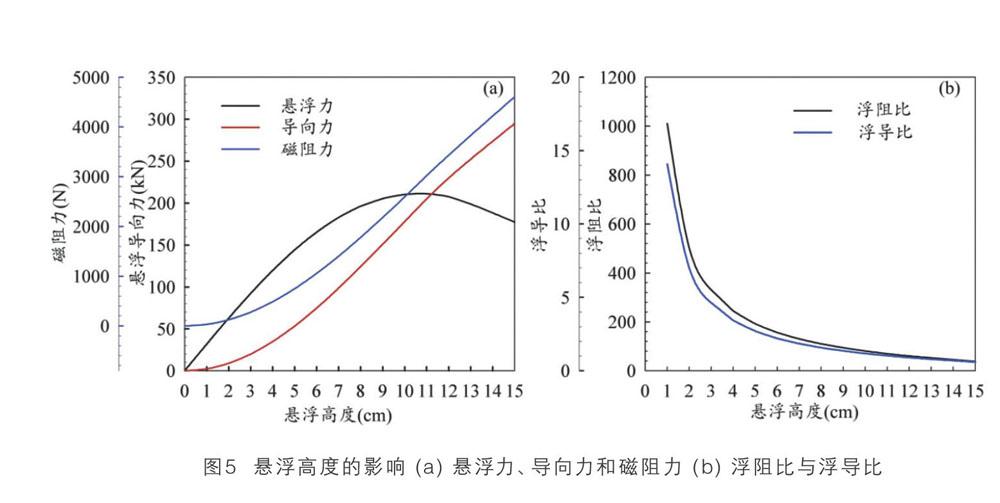
（4） 悬浮高度的影响

图5（a）和图5（b）分别为悬浮力、导向力和磁阻力以及浮阻比和浮导比随悬浮高度的变化曲线，其中8字线圈的横向间隙与竖向间隙均保持15cm和18cm不变，超导磁体的速度为1000km/h。由图5（a）知，导向力与磁阻力随悬浮高度的增大而增大，而悬浮力随悬浮高度的增大呈先增大后减小的趋势。当发生超导磁体载重增加或出现超导磁体部分失超出现悬浮力损失时，超导磁体的下沉高度会增大，若悬浮力不随下沉高度增大而增大，则必然发生超导磁体悬浮力难以平衡车重而发生碰撞事故。因此，实际设计中，起浮高度应设计在竖向刚度较大的区间，且为正向刚度。由图5（b）知，浮阻比与浮导比均随悬浮高度的增大而减小。

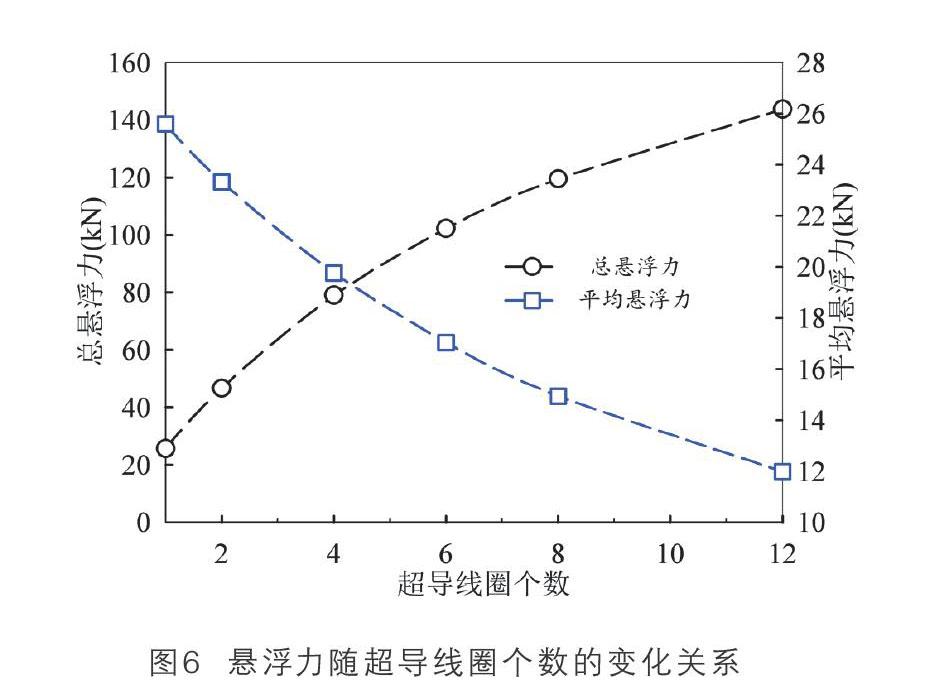
（5） 超导线圈个数的影响

超导磁体由若干几何尺寸与电气性能相同的超导线圈组成。图6为在不同超导线圈个数下，超导磁体所受的总悬浮力和单个超导线圈所受的平均悬浮力的变化曲线，其中8字线圈横向与竖向间隙分别为15cm和12cm，超导磁体悬浮高度和速度分别为3cm和500km/h。可知，超导磁体总悬浮力随超导线圈个数的增加而增大，而单个超导线圈所受的平均悬浮力随超导线圈个数的增加而减小。也就是说，超导磁体所受的总悬浮力与超导线圈的个数呈非线性关系。因此，在实际设计过程中，在满足极数的要求下，宜采用分布超导磁体替代集中分布超导磁体，如空间有一定间距的两组由4个超导线圈构成的超导磁体提供的悬浮力大于一组由8个超导线圈构成的超导磁体提供的悬浮力。

4 结论

本文针对日本MLU002型磁浮列车的超导电动悬浮系统进行了相关参数影响性分析，可得如下结论：

1）超导磁体悬浮力与导向力随速度的增大呈饱和趋势，而磁阻力随速度的增大逐渐减小;

2）悬浮力波动是超导电动悬浮系统的固有属性，波动频率与幅度与8字线圈的横向间隙有关而与8字线圈的竖向间隙无关。当8字线圈极距为超导线圈极距的三分之一时，悬浮力波动幅度最小。

3）悬浮力随悬浮高度的增大呈先增大后减小趋势，存在悬浮力最大的悬浮高度值。

4）超导磁体的超导线圈个数增加，超导磁体所受的总悬浮力增大而单个超导线圈所受的平均悬浮力减小，实际设计中多个超导线圈宜采用分布布置而不是集中布置。

责编/马铭阳