基于二级杠杆机构的二自由度微定位平台设计与分析
李 玄,周双武,路 松,丁冰晓
(1.吉首大学物理与机电工程学院,湖南吉首416000;2.澳门大学科技学院,澳门999078)
随着现代科学技术的快速发展,针对微机电技术、微加工与制造技术、微操作技术和微装配技术等的研究不断深入,现已进入微米级、量子级时代[1]。在光纤对接、激光加工以及微电机系统开发等领域均需要使用高精度微定位平台[2-5]。微定位平台是微定位系统的执行机构,主要由驱动部分和机械传动部分组成,其定位精度直接决定了微定位系统的精度[6]。目前,微定位系统主要有压电工作台型、电热微驱动工作台型以及电磁驱动工作台型等。其中,压电陶瓷驱动器因具有分辨率高、驱动力大和动态特性好等优点,成为了微定位领域应用较为广泛的驱动元件[7]。但是,压电陶瓷驱动器的行程较小且往往伴随多余的寄生运动,导致其驱动的微定位平台在工程上的应用受限。
为了解决这一问题,需借助放大机构来补偿压电陶瓷驱动器的输出位移[8],以扩大微定位平台的工作空间。常采用的放大机构有桥式放大机构、Scoot-Russel机构和杠杆机构[9]。围绕基于柔性结构的放大机构在微定位平台中的应用,国内外学者做了很多研究[10-11]。例如:天津大学的李政设计了一种用音圈电机驱动的二自由度微定位平台,其具有行程大、承载能力强、完全解耦等优点[12];西安电子科技大学的王子毅设计了一种柔顺精密二自由度定位平台,并通过有限元仿真分析得到了该平台的固有频率以及对应振型[13];Huang等设计了一种新型二自由度精密微定位平台,其运动行程可达19.2 μm×18.8 μm,定位误差小于5%[14];Lee等设计了一种基于桥式放大机构的二自由度微定位平台,并通过仿真与实验分析验证了该平台具有较大的行程以及较高的定位精度和分辨率[15]。上述二自由度微定位平台虽各具优点,但多数存在输出位移范围较小、整体刚度较小及结构复杂等问题。鉴于目前精密微定位平台的应用前景十分广阔,设计性能优异的微定位平台具有重要意义。
基于此,笔者拟基于杠杆原理和柔性结构,设计一种基于二级杠杆机构的由压电陶瓷驱动器驱动的二自由度微定位平台。首先,为提升微定位平台的动态特性,对杠杆机构进行优化;然后,为了解微定位平台的性能,对其输出位移放大倍数、刚度特征及固有频率进行理论分析;最后,为验证理论分析结果的准确性,对微定位平台的输出位移、静刚度与模态特性进行仿真分析。
1 二自由度微定位平台设计
1.1 柔性铰链选择
柔性铰链是柔性结构的最小单元,主要利用材料在结构薄弱部位的可塑性变形来传递力和运动,其具有体积小、无机械摩擦、无间隙和灵敏度高[16]等优点,广泛应用于微精密机械、光学、医学等领域。按缺口形式分类,柔性铰链主要可分为直梁型柔性铰链、椭圆型柔性铰链和正圆型柔性铰链,如图1所示。不同缺口型柔性铰链的刚度、转动范围和转动精度均不同,具体如表1所示。通过对比可以发现,椭圆型柔性铰链的性能介于直梁型柔性铰链与正圆型柔性铰链之间。为提升放大机构的性能,采用正圆型柔性铰链和直梁型柔性铰链作为放大机构的柔性结构,其中:正圆型柔性铰链主要用于杠杆机构,可提高转动精度;直梁型柔性铰链具有转动范围大、刚度小等特点,可用于位移导向机构。

图1 典型缺口型柔性铰链示意图Fig.1 Diagram of typical notched flexible hinges

表1 不同柔性铰链的性能对比Table 1 Comparison of performance of different flexure hinges
1.2 杠杆机构设计
杠杆机构是较常用的放大机构,相比于其他放大机构,其具有结构简单、制造方便和放大倍数易分析等优点,但其结构不紧凑,尤其是为了得到大放大比,需要增大机构的整体尺寸。为有效平衡杠杆机构尺寸和微定位平台输出位移之间的关系,需选择具有合适放大级数的杠杆机构。一级杠杆机构结构简单,但难以得到足够大的输出位移;三级或多级杠杆机构的结构不够紧凑,易产生寄生运动。鉴于此,选择二级杠杆机构作为微定位平台的放大机构。同时,为了提高微定位平台的响应速度,对传统杠杆机构的几何形状进行优化。图2所示为3种不同类型的杠杆机构的结构及其力驱动形式,其中图2(a)、(b)为新型杠杆机构,图2(c)为传统杠杆机构。图2中:小黑点表示杠杆机构的质心,m表示杠杆机构的质量,r1、r2和r3分别表示3种不同类型杠杆机构的质心与转动轴之间的距离,F表示驱动力。

图2 不同类型杠杆机构的结构与力驱动形式对比Fig.2 Comparison of structure and force driving form of different types of lever mechanisms
杠杆机构的转动惯量J为:

则图2所示的3种杠杆机构的转动惯量分别为:

由r1<r3<r2可得:

在相同的驱动力F和力矩τ的作用下,不同杠杆机构的终端加速度ai(i=1,2,3)为:

根据式(3)可知a1>a3>a2,由此说明相比于图2(c)所示传统杠杆机构和图2(b)所示的新型杠杆机构,图2(a)所示的新型杠杆机构可更有效缩短反应时间。因此,采用图2(a)所示的新型杠杆机构有利于提高微定位平台的响应速度,进而提升微定位平台的整体性能。
1.3 微定位平台设计
基于新型二级杠杆机构的二自由度微定位平台的结构如图3所示,整个微定位平台的外形尺寸为235mm×235mm×10mm,其内部含有36个柔性铰链,由压电陶瓷驱动。二自由度微定位平台采用并联形式,由4个支链(2个二级杠杆机构和2个位移导向机构)连接末端工作平台和基座,具有刚度大、承载能力强、无积累误差和响应速度快等优点。二自由度微定位平台利用二级杠杆机构放大输入位移,在每个二级杠杆机构的第1级杠杆的柔性铰链支点附近添加1对固定孔,以有效防止在杠杆机构运转时柔性铰链因受到较大的拉伸而导致微定位平台整体发生大的形变,从而影响该方向输出位移的放大;同时,固定孔中心应适当偏离柔性铰链中心,以防止柔性铰链因拉伸过大而发生断裂。在二自由度微定位平台的x、y方向上,压电陶瓷驱动器输入的位移经二级杠杆机构放大后传至末端工作平台,再通过位移导向机构的定向传导,消除多余的耦合寄生运动后输出。
2 二自由度微定位平台性能理论分析
为进一步了解二自由度微定位平台的各项性能,对该微定位平台的位移放大倍数、静力学特性(刚度特征)以及动力学特性(固有频率)进行理论分析。
2.1 位移放大倍数分析

图3 基于二级杠杆机构的二自由度微定位平台整体结构示意图Fig.3 Overall structure diagram of two-DOF micro-positioning platform based on two-level lever mechanism
二级杠杆机构作为微定位平台的位移放大、传递机构,采用完全对称结构,以避免应力集中和确保机构不受切向破坏力的影响,同时使非驱动位移方向上的受力抵消,不产生附加位移,以提高运动精度。二自由度微定位平台中二级杠杆机构的尺寸参数如图4所示。图4中:l1为位移输入点S到柔性铰链A的水平距离;l2为柔性铰链A到柔性铰链B的水平距离;l3为柔性铰链C到柔性铰链D的水平距离;l4为柔性铰链D到柔性铰链G的水平距离;l5为连接工作平台的每根杆的长度;l6为位移导向机构中直梁型柔性铰链的缺口长度。为了方便计算,取二级杠杆机构的一侧进行分析,其放大原理如图5所示:输入位移Δd经由柔性铰链A、B组成的第1级杠杆和由柔性铰链C、D、G组成的第2级杠杆进行放大处理,最终在柔性铰链H处输出位移Δy。图5中:Δa表示输入位移经第1级杠杆放大后的输出位移,同时也是第2级杠杆的输入位移;θ1表示第1级杠杆的转角;θ2表示第2级杠杆的转角。

图4 二自由度微定位平台中二级杠杆机构的尺寸参数Fig.4 Dimension parameters of two-level lever mechanism in the two-DOF micro-positioning platform
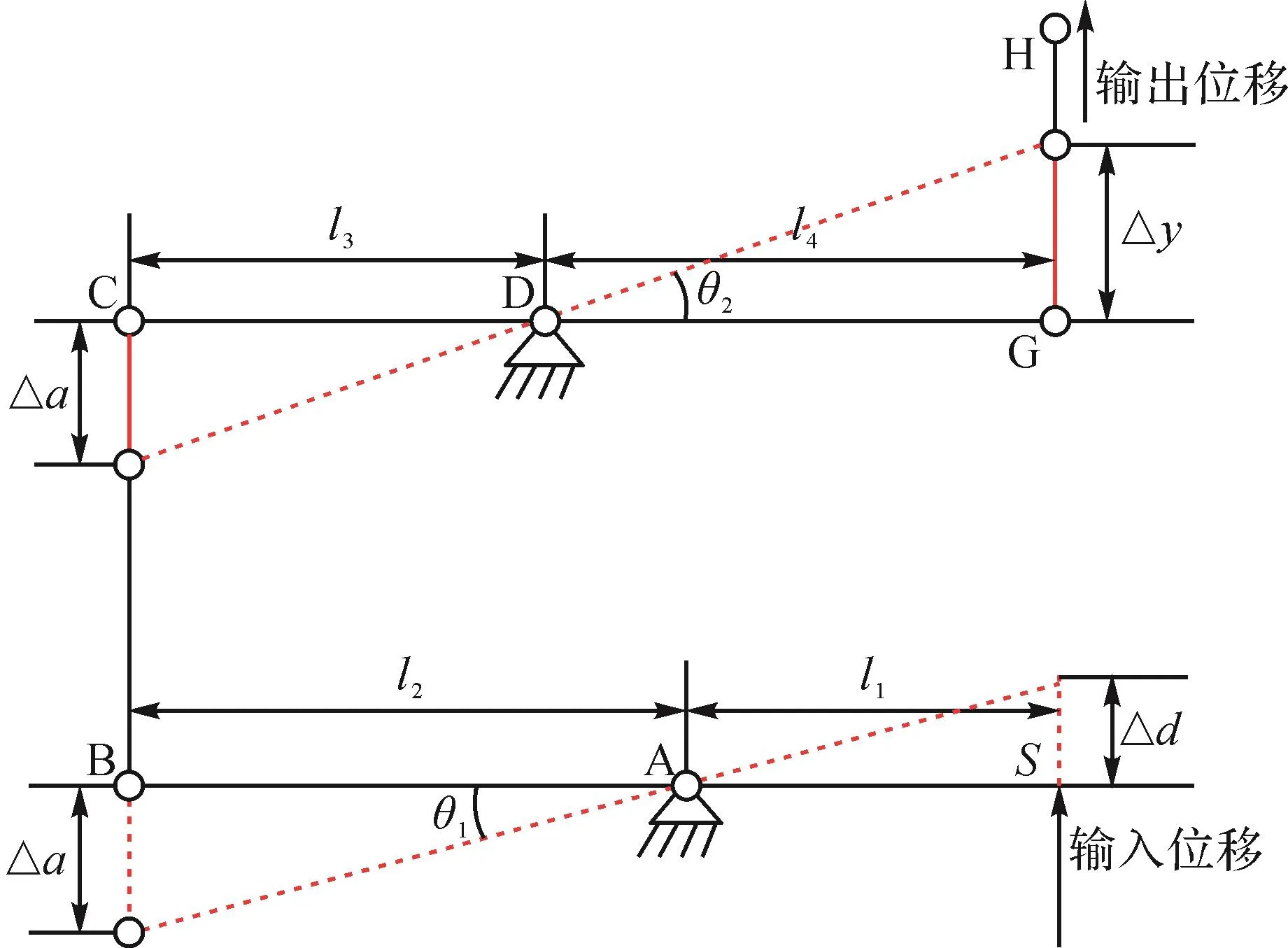
图5 二级杠杆机构的放大原理Fig.5 Amplification principle of two-level lever mechanism
根据图5所示的二级杠杆机构放大原理和相似三角形理论,可得第1级杠杆的位移放大倍数为[17]:

同理可得第2级杠杆的位移放大倍数为:

综上可得二级杠杆机构的位移放大倍数为:

2.2 静力学分析
为得到二自由度微定位平台输出位移与驱动力的关系,对其进行静力学分析。驱动力主要用于驱使柔性铰链转动,因此需要先计算柔性铰链的转动刚度。如图6所示,以柔性铰链连接杆截面中心为原心,中性轴方向为y轴方向,柔性铰链两端连接方向为x轴方向,与柔性铰链转动平面相互垂直的方向为z轴方向,建立直角坐标系,其中:t、h、b分别为柔性铰链的最小厚度、高度和宽度,R为正圆型柔性铰链的圆弧半径,2w为直梁型柔性铰链中间梁杆的长度,Mz为柔性铰链转动时受到的力矩。

图6 柔性铰链几何模型Fig.6 Geometric model of flexure hinges
由图6可知,正圆型柔性铰链和直梁型柔性铰链的转角刚度k1、k2分别为[18]:


式中:E表示材料的弹性模量;I为直梁型柔性铰链中间梁杆截面上y方向的惯性矩。
对二自由度微定位平台y方向的刚度进行分析,为方便计算,取微定位平台的左侧进行分析,具体参数如图7所示。

图7 二自由度微定位平台静力学分析参数Fig.7 Static analysis parameters of two-DOF micro-positioning platform
微定位平台在驱动力作用下运转做功时会产生相应的动能与势能,分别可表示为:

式中:T、U分别为微定位平台的动能和势能;m1为连接二级杠杆机构与工作平台的每根杆的质量;J4、J5、J6分别为第1级杠杆、第2级杠杆和x方向上与工作平台相连的每根杆的转动惯量;θ3为x方向上与工作平台相连的每根杆的转动角度。
同时,依据微定位平台的输出位移Δy,可得:

由于微定位平台的输出位移Δy很小,可得:


将式(15)至式(17)代入式(10)和(11)可得:

式中:M表示二自由度微定位平台的质量;K表示二自由度微定位平台y方向的刚度。
综上,二自由度微定位平台y方向的刚度K可表示为:
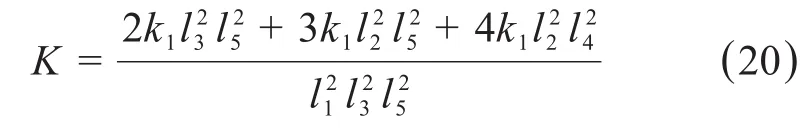
二自由度微定位平台的结构对称,其x方向的刚度与y方向的刚度相同,不再重复推导。
2.3 动力学分析
对二自由度微定位平台进行动力学分析,以得到其固有频率。由静力学分析可知,该微定位平台的质量M可表示为:

基于拉格朗日公式,得到该微定位平台的动力学方程:
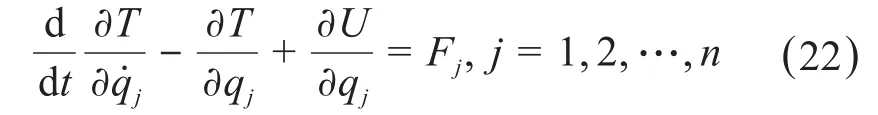
式中:qj为广义坐标;Fj为非有势力;n为微定位平台的自由度数。
由此可得二自由度微定位平台在位移输出方向上的动力学方程为:

3 二自由度微定位平台性能仿真分析
为了验证理论分析结果的准确性,利用有限元分析软件Workbench对二自由度微定位平台的位移放大倍数、静力学特性和动力学特性进行仿真验证。二自由度微定位平台的材料为铝合金7075-T6(SN),其弹性模量E=72 GPa,泊松比μ=0.33,屈服强度σ=505 MPa。二自由度微定位平台的尺寸参数如表2所示。
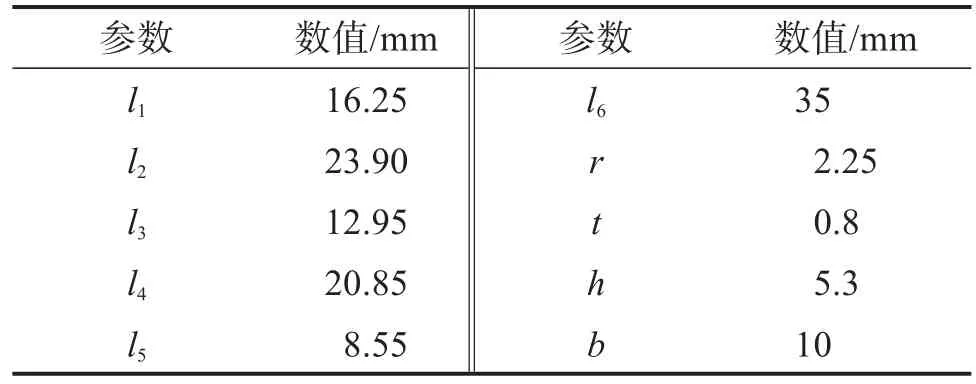
表2 二自由度微定位平台的尺寸参数Table 2 Dimension parameters of two-DOF micro-positioning platform
3.1 位移仿真分析
利用有限元分析软件Workbench对二自由度微定位平台进行位移仿真分析。将二自由度微定位平台的三维模型(Solidworks中建立)导入Workbench后建立有限元模型,并在所有定位孔的内圆柱面施加固定约束,在加载节点处进行位移加载。二自由度微定位平台的位移云图及应变云图如图8所示。
为验证二自由度微定位平台的稳定性,对其y方向的输入位移和输出位移进行分析,结果如表3所示。由表3可知,该二自由度微定位平台在y方向上输出位移时,会在x方向上产生一定的耦合位移xc,但相比于实际需要的输出位移yout,xc非常微小,可以忽略不计,这表明该微定位平台具有较高的稳定性。
3.2 静力学仿真分析
为了验证二自由度微定平台理论刚度模型的准确性,对其进行静力学仿真分析。不同驱动力下二自由度微定位平台输出位移的理论值与仿真值对比如图9所示。
由图9可知:二自由度微定位平台的输出位移与驱动力呈线性相关关系,输出位移随驱动力的增大而增大,其仿真刚度为7.57 N/μm。根据式(20)计算得到该微定位平台的理论刚度为6.86 N/μm,仿真刚度与理论刚度比较接近,其相对误差为9%;随着驱动力的增大,理论刚度与仿真刚度的差异逐渐增大,这是因为微变形和微运动对输出位移的影响会随驱动力的增大而增大,而理论分析时忽略了微变形、微运动的影响,从而导致差异变大。但总体而言,理论分析结果具有较高的可靠性,可为微定位平台刚度分析提供理论指导。
3.3 动力学仿真分析

图8 二自由度微定位平台的位移云图及应变云图Fig.8 Displacement nephogram and strain nephogram of two-DOF micro-positioning platform
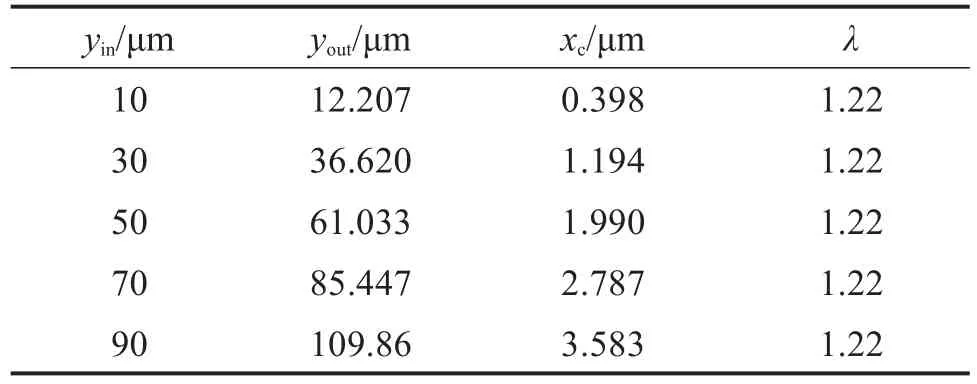
表3 二自由度微定位平台y方向输出位移仿真结果Table 3 Simulation results of y-direction output displacement of two-DOF micro-positioning platform
为验证二自由度微定位平台动力学特性理论分析结果的准确性,对该微定位平台进行动力学仿真分析,主要通过模态和固有频率来表征其动力学性能,仿真结果如图10所示。由图10可以看出,二自由度微定位平台的第1阶共振频率为638.21 Hz,在该频率下,工作平台沿z方向发生了偏移;在第2、第3阶频率下,工作平台沿x、y方向产生平移;在第4、第5、第6阶频率下,工作平台沿z方向产生平移。在工作平台沿x、y方向作平移运动的情况下,微定位平台的固有频率比较接近,表明在第2、第3阶频率下,该微定位平台具有相似的动力学特性。

图9 不同驱动力下二自由度微定位平台输出位移的理论值与仿真值对比Fig.9 Comparison of theoretical and simulated output displacements of two-DOF micro-positioning platform under different driving forces
4 结 论
本文设计了一种基于二级杠杆机构的二自由度微定位平台。通过对该微定位平台的位移放大倍数、刚度及固有频率进行理论分析和仿真分析发现,该微定位平台具有稳定性好、刚度大和动力学性能良好等优点。本文采用的微定位平台结构设计和分析方法具有一定的实用价值。
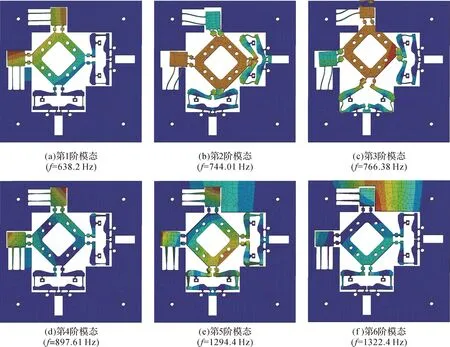
图10 二自由度微定位平台动力学仿真结果Fig.10 Dynamics simulation results of two-DOF micro-positioning platform

