数控机床液体静压导轨结构的优化设计

李典伦，黄 华，邓文强

（兰州理工大学机电工程学院，甘肃兰州730000）

机床导轨的性能会直接影响机床的加工精度［1］。与普通导轨相比，液体静压导轨具有摩擦阻力小、精度高等特点，被广泛应用于精密机床［2］。为提升导轨的性能，国内外学者对其材料、制造工艺及结构等进行了大量研究。例如：Lai等［3］采用K9玻璃光学材料制造导轨，该导轨的工作表面误差和气膜厚度均小于传统的空气静压导轨，精度、刚度和承载能力均大于传统的铸铁导轨；Chen等［4］改善了制造直线运动导轨的传统冲压技术，实现高精度、快速制造，并有效消除了导轨的断裂现象；Soshi等［5］基于传统滑动面加工磨削方法，通过在铸铁材料中添加铝和镁来提高机床的整体加工性能和生产率，并采用立方氮化硼铣削加工方法，以使刀具不易磨损和具有恒定的表面粗糙度；张耀满等［6］分析了在高载荷和高温情况下，滚动直线导轨热变形对其接触刚度的影响以及不同垂直载荷下导轨的温度分布，为导轨设计奠定了理论基础；Liu等［7］为了控制由机械加工力引起的振动，研制了一种新型的磁流变液静压导轨系统，该导轨具有较佳的静态刚度和较高的阻尼；李天箭等［8］提出了4种微结构表面来减小流体阻力，通过对比发现利用V形沟槽构建微结构表面有利于减阻；夏毅敏等［9］利用流体分析软件对节流器结构与Nanosys-1000超精密加工机床液体静压导轨的承载能力进行了分析，并确定了节流器的最优结构参数；陈东菊等［10］根据速度滑移算法以及Navier-Stokes方程，对气膜的压强分布进行了仿真分析，并通过试验验证了气膜厚度的变化规律。

综合来看，机床液体静压导轨的静刚度、表面粗糙度及生产率等已逐渐改善，但导轨的减阻效果、热性能等仍显不足，目前的研究仅仅验证了V形沟槽的减阻效果以及利用仿真软件分析了不同温度分布下导轨的变形，没有验证其他微结构的减阻效果，且未从根本上消除由温差变化引起的变形［11］。针对这一现象，笔者提出了一种采用树脂混凝土制造液体静压导轨滑块的方法，并通过在滑块表面构造U-V形微结构来实现减阻，以提高液体静压导轨的整体性能。

1 液体静压导轨的工况分析与结构设计

传统的铸铁和花岗岩材料虽具有刚性好、强度大、成本低等特点，但其热性能相对较差，且容易发生热变形。为了提升机床的综合性能，以某具体加工工况为例，对液体静压导轨的材料及结构尺寸进行重新选择和设计，以提高其热性能、动态性能及整体精度。

1.1 液体静压导轨工况分析

某型号卧式加工中心采用由树脂混凝土制成的液体静压导轨，并在其表面进行微结构减阻设计。卧式加工中心的结构如图1所示。在机床加工过程中，液体静压导轨用于承受、固定及引导立柱，以减小立柱与床身之间的摩擦，并将刀具与工件的作用力传递至床身。立柱下方有2条支承导轨，每条导轨上有2个滑块与之相连。

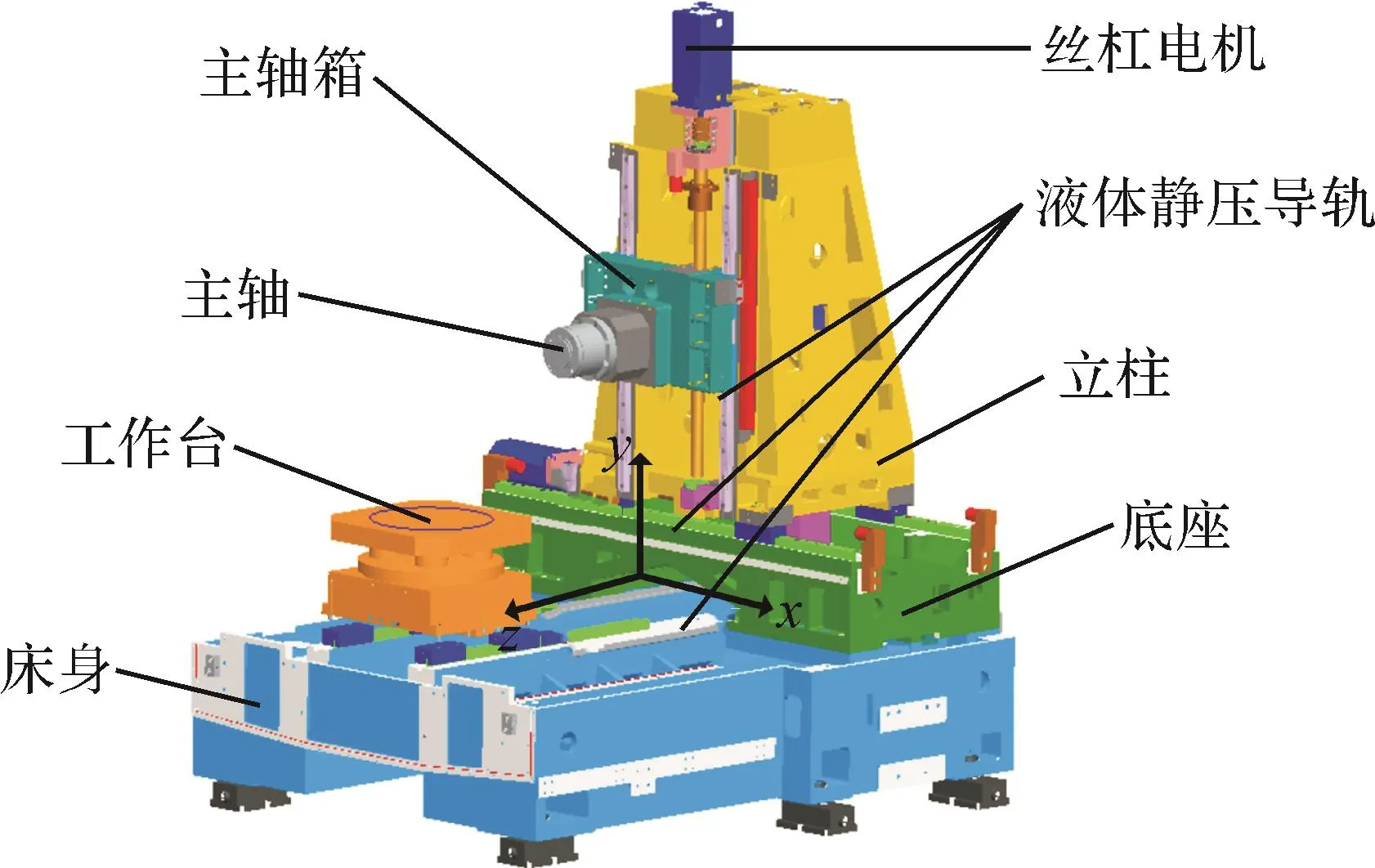
图1 卧式加工中心结构示意图Fig.1 Structure diagram of horizontal machining center

以典型切削工况为例，在某主要工序中：背吃刀量ap=5mm，切削量f=0.5mm/r，切削速度vc=150m/min，其他参数由查阅相关设计手册而得。切削力Fc、背向力Fp、进给力Ff的计算公式如下［12］：

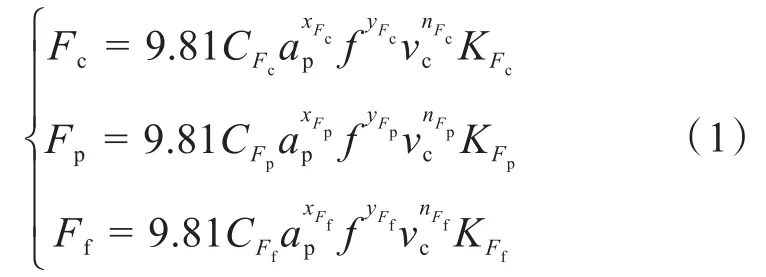
式中：CFc、CFp、CFf表示由被加工材料和切削条件决定的系数；xFc、yFc、nFc表示刀具材料及加工形式对切削力的影响指数；xFp、yFp、nFp表示刀具材料及加工形式对背向力的影响指数；xFf、yFf、nFf表示刀具材料及加工形式对进给力的影响指数；KFc、KFp、KFf表示各种因素对切削力影响的修正系数。

根据式（1）计算可得：Fc=2799.1N，Fp=671.77N，Ff=1074.9N。整个主轴箱系统及液体静压导轨的重量约为8 000 N，立柱的重量约为17 500 N，则立柱下方液体静压导轨（以下简称为液体静压导轨）承受系统总重量G≈25 500 N。在切削过程中，距液体静压导轨表面500 mm处受到的进给力Ff≈1074.9N。液体静压导轨的受力分析如图2所示。

1.2 液体静压导轨油垫结构设计

在上述工况条件下，为了保证液体静压导轨的承载量，对该型号卧式加工中心液体静压导轨的结构进行改进设计。在机床运行过程中，液压油通过节流器、矩形油垫进入导轨油腔，当经节流器节流后的液压油的压力大于导轨所承受的载荷时，导轨浮起，导轨油膜形成。与单向矩形平面支承油垫相比，对置双向矩形平面油垫具有较大的刚度和较高的稳定性，并能承受一定的倾覆载荷，故采用对置双向矩形平面油垫，其液压原理如图3所示。

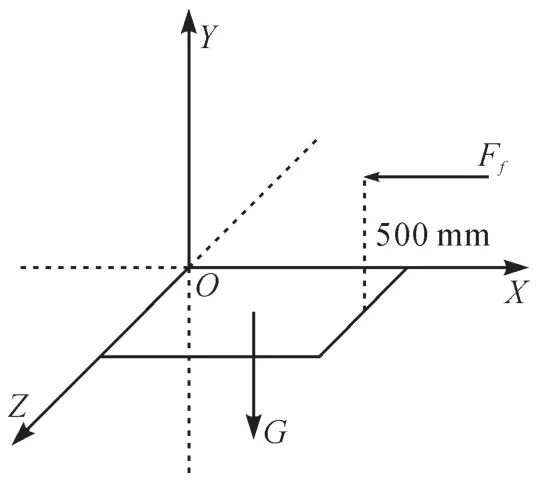
图2 液体静压导轨的受力分析Fig.2 Force analysis of hydrostatic guideway

图3 对置双向矩形平面油垫的液压原理示意图Fig.3 Hydraulic principle schematic diagram of opposed bidirectional rectangular plane oil cushion

如图4所示，将2个尺寸相同的矩形油垫对置放在液体静压导轨两侧，当无载荷作用在液体静压导轨上时，滑块与液体静压导轨间的油膜厚度为h，处于平衡状态；当有外载荷作用在液体静压导轨上时，液体静压导轨整体下降e，然后重新达到平衡状态，此时滑块下表面的油膜厚度为h-e，滑块上表面的油膜厚度为h+e。当液体静压导轨处于平衡状态时，可将矩形油垫看作等压矩形，由于其外圈有封油边，为方便计算矩形油垫的承受载荷，引入有效承载面积Ae，如图5所示。

由上文的工况分析可知，该机床液体静压导轨承受的总载荷为25 500 N，因导轨由4个滑块共同支撑，则每个滑块承受的载荷W=6 375 N。采用恒压供油方式，油压p=1.5 MPa，根据公式W=p⋅Ae，得出矩形油垫的有效承载面积Ae=42.5cm2。经初步分配得出：矩形油垫有效承载面的长度为85 mm，宽度为50 mm；封油边的长度l=92 mm，宽度b=60 mm；封油边长边的厚度l1=7 mm，封油边宽边的厚度b1=10 mm，如图6所示。

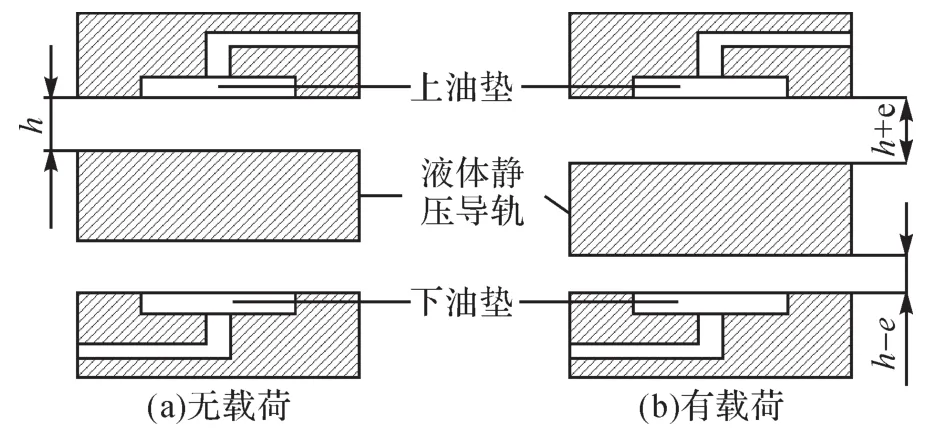
图4 液体静压导轨表面油膜厚度示意图Fig.4 Schematic diagram of oil film thickness of hydrostatic guideway

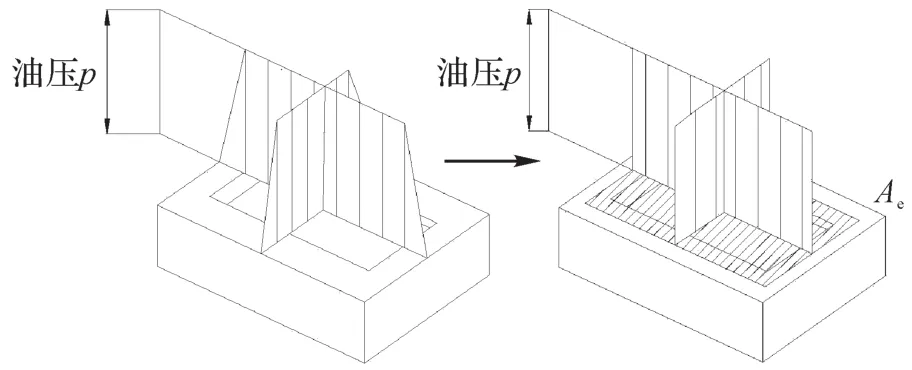
图5 矩形油垫有效承载面积示意图Fig.5 Schematic diagram of effective load area of rectangular oil cushion

图6 典型切削工况下矩形油垫尺寸示意图Fig.6 Schematic diagram of rectangular oil cushion size under typical cutting condition

为了求解矩形油垫的液阻比λ，需先选择合适的小孔节流孔径dc，其需满足的条件为：

式中：h为油膜厚度，取h=30 μm；ρ为液压油密度，取ρ=8.58×10-6N⋅s2/cm4；α为流量系数，取α=0.6～0.7；μ为液压油动力黏度，取μ=5.75×10-7N⋅s/cm2。

经过计算得出dc≥0.41mm，则取小孔节流孔径dc=0.5mm。

为了验证参数设计的合理性［13］，将计算得到的液阻比λ与最佳液阻比λ0=0.707作比较。液阻比λ的计算公式为：

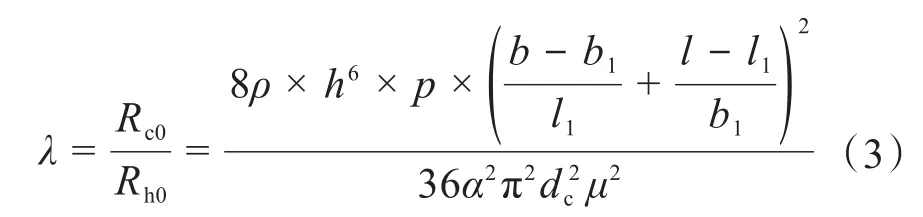
式中：Rc0为节流器液阻；Rh0为封油边初始液阻。

根据式（3）计算得到液阻比λ=0.691，与最佳液阻比λ0相近，说明矩形油垫的尺寸设计合理［14］。

液体静压导轨及滑块的三维模型如图7所示。

图7 液体静压导轨及滑块的三维模型Fig.7 Three-dimensional model of hydrostatic guideway and slider

1.3 液体静压导轨结构的强化设计

树脂混凝土是一种具有良好力学特性的复合材料［15］，由12%的环氧树脂、1%的固化剂、2%的稀释剂、1%的增韧剂、80%的骨料及4%的填料组成，其弹性模量约为灰铸铁材料的1/4，密度约为灰铸铁材料的1/3。树脂混凝土的性能参数如表1所示。

表1 树脂混凝土的性能参数Table 1 Performance parameters of resin concrete

为了提高液体静压导轨的热性能，设计了一种由树脂混凝土制成的液体静压导轨（以下简称为树脂混凝土液体静压导轨）。由于树脂混凝土的弹性模量较小，要想保证液体静压导轨的刚度，需对其内部进行结构强化设计，因此设计了一种钢结构支承件，其结构如图8所示。将钢结构支承件内嵌进液体静压导轨中，以提高导轨的刚度。

2 液体静压导轨的静力学和热力学性能分析

2.1 液体静压导轨的静力学分析

图8 树脂混凝土液体静压导轨内部钢结构支撑件Fig.8 Strutting piece with embedded steel structure of hydrostatic guideway made by resin concrete

为了验证内嵌钢结构的树脂混凝土液体静压导轨的静态性能，利用有限元软件Workbench对树脂混凝土液体静压导轨和花岗岩液体静压导轨进行静力学分析。由上文分析可知，在典型切削工况下，每个液体静压导轨滑块受到方向向下的载荷W=6375N，在距液体静压导轨表面500 mm处受到进给力Ff=1074.9N。设树脂混凝土液体静压导轨及花岗岩液体静压导轨的初始边界条件相同，底部均设置全约束。液体静压导轨及滑块的变形云图如图9所示。

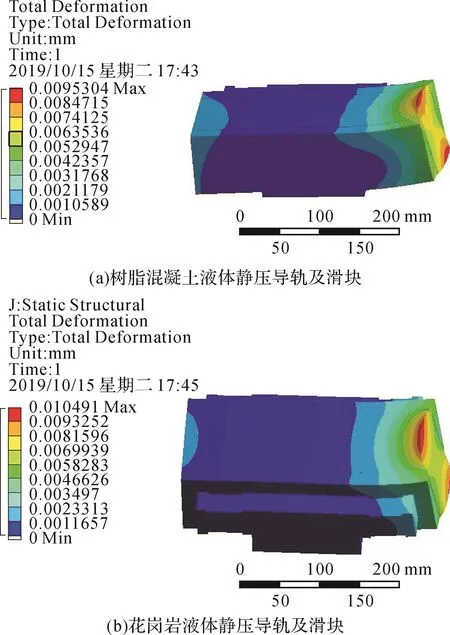
图9 液体静压导轨及滑块的变形云图Fig.9 Deformation nephogram of hydrostatic guideway and slider

由图9可知，2种液体静压导轨的最大静变形均出现在导轨右上角处，这说明进给力Ff对导轨及滑块的影响较大。树脂混凝土液体静压导轨的最大静变形量小于花岗岩液体静压导轨，表明钢结构支撑件起了一定的作用。液体静压导轨的静力学分析结果如表2所示。

表2 液体静压导轨的静力学分析结果Table 2 Statics analysis result of hydrostatic guideway

2.2 液体静压导轨的主要热源和边界条件分析

数控机床的误差主要为运动误差、热误差、控制误差和力误差等，其中热误差占总误差的40%～70%［16］。为了验证树脂混凝土液体静压导轨的热性能，利用有限元软件Workbench对树脂混凝土液体静压导轨和花岗岩液体静压导轨进行稳态、瞬态热分析。

数控机床的主要热源为切削热、主轴系统发热以及运动副间的摩擦热［17］。在分析液体静压导轨的热性能时，只须分析导轨与立柱间的摩擦热及周围环境对导轨的热影响，其他热源可忽略不计。

液体静压导轨的力学平衡方程为：

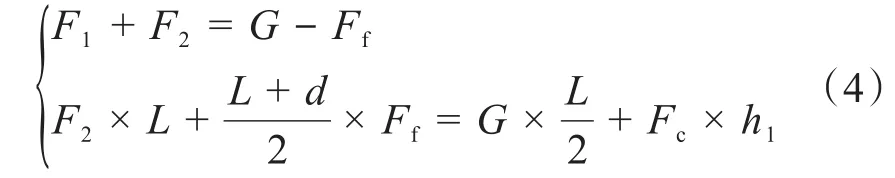
式中：F1为近刀具端导轨的受力，F2为远刀具端导轨的受力，经计算，F1=11 308.3 N，F2=13 116.8 N；d为机床刀具的直径；h1为刀具与导轨的垂直距离；L为立柱下2条导轨的间距。

由于每条液体静压导轨都与2个滑块相连，为方便计算，选取受力较大的1条液体静压导轨进行分析。对于某一个滑块，其摩擦热为：

式中：F3为该条导轨所承受的载荷；μ2为液体静压导轨的摩擦系数；v为液压油的流速；S为液体静压导轨矩形油垫的面积。

经计算得到液体静压导轨与立柱间摩擦产生的热量q=7.07×10-4W/mm2。

液体静压导轨的外表面暴露于空气中，其一部分热量会被带走，为自然对流换热。为了模拟相关条件，利用标准努谢尔特准则和格拉晓夫数方程计算对流换热系数，计算公式分别为：

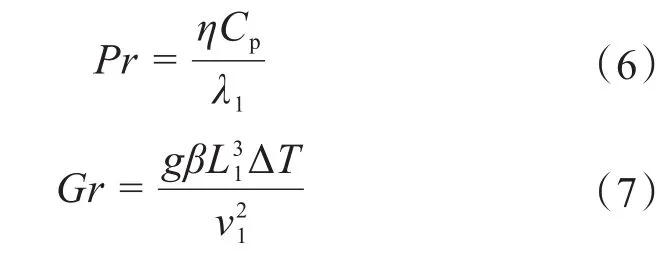
式中：Pr为普朗特数；η为流体的动力黏度；Cp为流体的比定压热容；λ1为流体的导热系数；Gr为格拉晓夫数；g为重力加速度；β为流体热膨胀系数；L1为特征尺寸；ΔT为流体与壁面的温差；v为流体的运动黏度；Nu为努塞尔数；C、n为常数；h2为对流换热系数；L2为液体静压导轨宽度。

经计算得出液体静压导轨外表面对流换热系数ha=2.15×10-5W/(mm2⋅°C)，内表面对流换热系数hb=4.68× 10-5W/(mm2⋅°C)。

2.3 液体静压导轨的稳态和瞬态热分析

利用有限元软件Workbench对树脂混凝土液体静压导轨及花岗岩液体静压导轨进行稳态、瞬态热分析。2种液体静压导轨模型的边界条件相同，其稳态热分析结果如图10所示。由图可知，树脂混凝土液体静压导轨的最高温度小于花岗岩液体静压导轨的最高温度，且其温差较小，两者的最高温度均出现在内嵌的钢结构支撑件处。

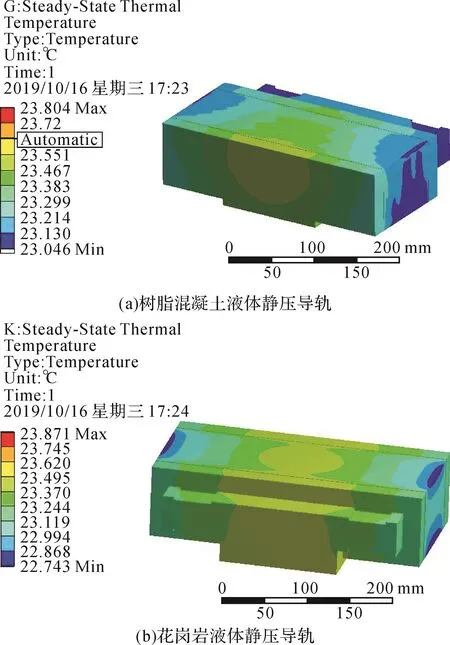
图10 液体静压导轨的稳态热分析结果Fig.10 Steady state thermal analysis result of hydrostatic guideway

为了进一步验证树脂混凝土液体静压导轨的热性能，在稳态热分析的基础上，对其进行瞬态热分析。液体静压导轨的瞬态温度如图11所示，其中在第2.0秒、第11.1秒、第82.5秒、第162.5秒、第200.0秒五个时刻的温差如表3所示。

表3 液体静压导轨的瞬态温差Table 3 Transient temperature difference of hydrostatic guideway 单位：℃

图11 液体静压导轨的瞬态温度分布Fig.11 Transient temperature distribution of hydrostatic guideway

温差是导致导轨热变形的重要因素之一，温差越小，导轨热性能越稳定。由表3所示的2种液体静压导轨的温差可知，树脂混凝土液体静压导轨的温差较小，表明其热性能比花岗岩液体静压导轨稳定。

3 液体静压导轨减阻微结构的设计

液体静压导轨与滑块之间的阻力直接影响机床整体的稳定性及精度。为了减小阻力，在液体静压导轨表面设计了一种U-V形沟槽减阻微结构并作用于滑块表面以提升机床的运动性能。

3.1 液体静压导轨减阻微结构计算区域设计

为了防止减阻微结构对油膜产生影响，在离矩形油垫2 mm的区域设计减阻微结构，且添加减阻微结构后导轨的表面仍为光滑平面［18］。

考虑到微结构加工成本和导轨宽度，在液体静压导轨表面加工一个长为6 mm的微结构，其前后各有长为3 mm的缓冲区域，最终微结构的计算区域为2.5 mm×12 mm，并以此建立减阻模型。图12所示为V形沟槽微结构的计算区域。

利用ICEM CFD软件对减阻模型进行网格划分，将微结构处的网格细化，以保证减阻模型的准确性。由于油膜为30μm，而减阻微结构的长度为6 mm，为了能用宏观流体力学分析模型分析减阻微结构，则需保证克努森数Kn＜0.001，即：

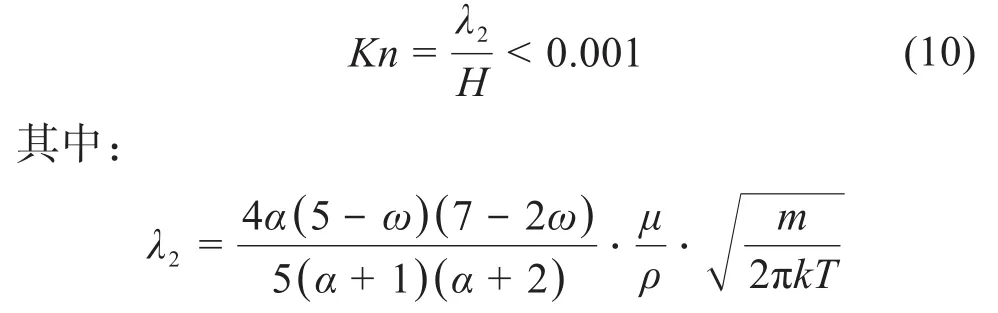
式中：λ2为分子平均自由程；H为单个微结构的深度；α为液压油运动黏度；ω为液压油黏性系数；m为液压油的相对黏性质量；T为液压油温度；k为波尔兹曼常数。

经计算得H≥1.29μm，表明单个微结构的深度须大于1.29μm，才能用宏观流体动力学模型来分析减阻微结构。

3.2 减阻微结构的性能分析

在矩形沟槽、V形沟槽、U形沟槽和Space-V形沟槽中，V形沟槽的减阻效果最佳［8］，U形沟槽的入口压力值较小，V形沟槽的出口压力值较大，因此，为了使总压降较小，设计了一种U-V形沟槽，如图13（a）所示。其中U形沟槽的深度为5μm，其余每个V形沟槽的深度为10μm、宽度为15μm，使其在液体静压导轨上的减阻效果比V形沟槽的减阻效果更加明显。

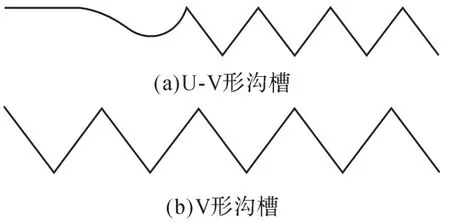
图13 微形沟槽结构示意Fig.13 Schematic of micro-groove structure

根据入口压力与出口压力，得出计算区域的总压降。由于压降与阻力成正相关，则可根据压降的大小来反映通道内的阻力大小：总压降越小，则通道内的阻力越小。

式中：Δp为计算区域的总压降；pin为计算区域的进口压力；pout为计算区域的出口压力；Δpsmooth为光滑通道内的总压降；Rcf为减阻率，Rcf越大，说明减阻效果越好，若Rcf为负，则说明有增阻效果。

利用ANSYS CFX软件对具有U-V形沟槽、V形沟槽和无沟槽（光滑通道）区域的压力进行求解，得到其压力分布云图，结果如图14所示。

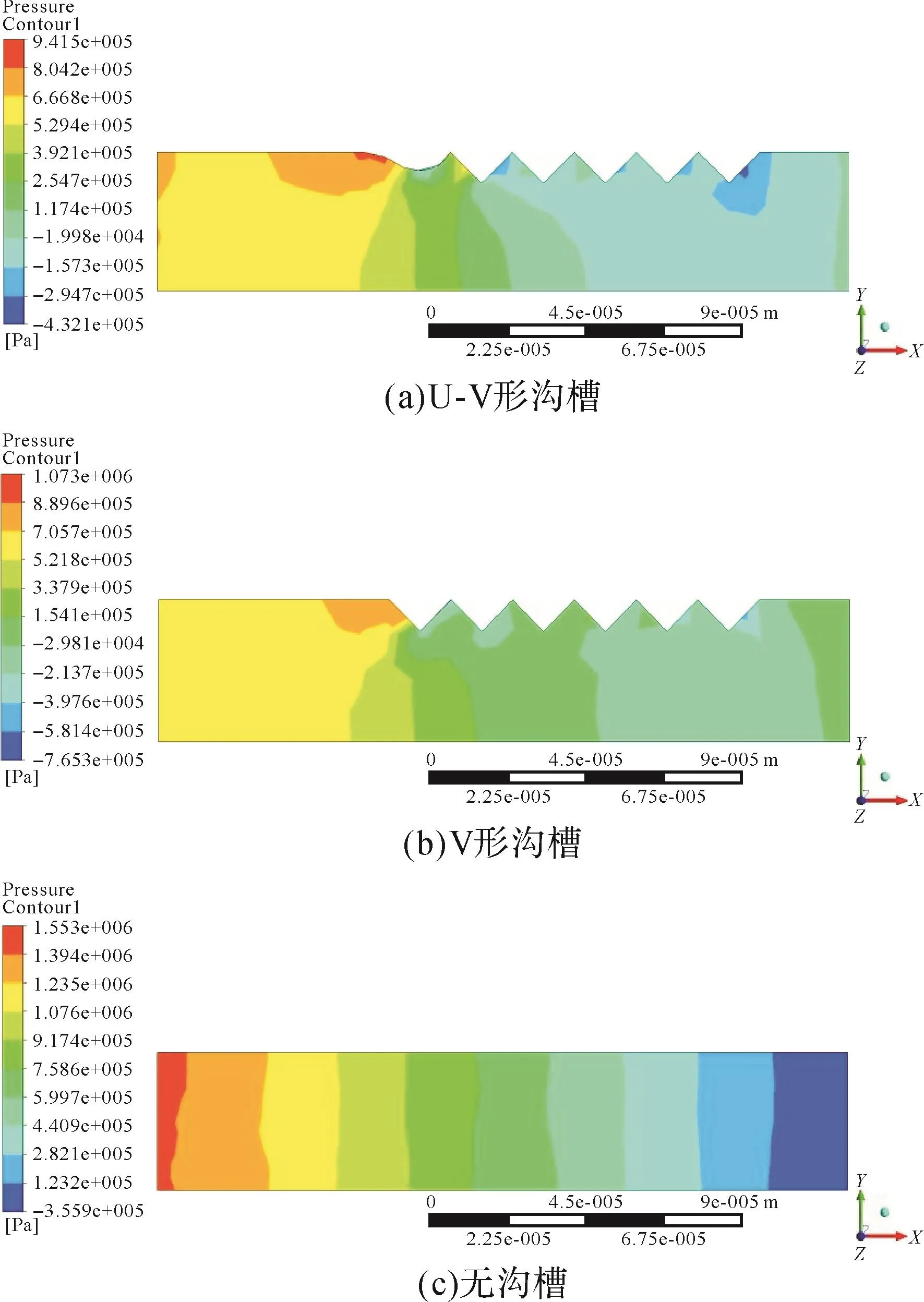
图14 微结构区域的压力分布云图Fig.14 Pressure distribution cloud in micro-structure area

由图14可知，具有U-V形沟槽和V形沟槽区域的压降均小于光滑通道的压降。其压降和减阻率如表4所示，由表可知，具有U-V形沟槽区域的减阻率略大于V形沟槽，表明U-V形沟槽和V形沟槽均具有减阻效果，且U-V形沟槽的减阻效果更加明显。

表4 微结构区域的压降和减阻率对比Table 4 Pressure drop and drag reduction rate of micro-structure area

4 结 论

采用内嵌钢结构的树脂混凝土制作了精密液体静压导轨，并在其表面设置了减阻微结构，使得其热性能、动态性能及减阻性能都有了较大提升，并通过仿真分析验证了该结构的可行性，得出结论以下：

1）在相同工况条件下，树脂混凝土液体静压导轨的最大静变形比花岗岩液体静压导轨的小，表明树脂混凝土液体静压导轨具有较高的强度和刚度。

2）树脂混凝土液体静压导轨的温差比花岗岩液体静压导轨的小，表明树脂混凝土液体静压导轨具有良好的热性能，可大大降低因温差而导致的热变形。

3）具有U-V形沟槽区域的减阻率为28.2%，具有V形沟槽区域的减阻率为4.1%，说明在液体静压导轨表明设置减阻微结构能有效减小导轨与滑块间的阻力，提高液体静压导轨的综合性能。