基于给定非线性刚度的柔顺驱动器设计及性能评估
宋智斌,胡秀棋
(天津大学机械工程学院机构理论与装备设计教育部重点实验室,天津300072)
近年来,随着机器人技术的发展,人机共融的场景逐渐增多,这对人机交互的安全性提出了较高的要求[1-3],机器人关节的柔顺性显得尤为重要。此外,仿生机器人关节更须具有一定的柔顺性,才能实现适应环境的仿生运动[4]。
机器人关节的柔顺性可以通过力/力矩控制来实现(即主动型柔顺),也可以利用机械结构的固有柔性来实现(即被动型柔顺),本文主要讨论后者。串联弹性驱动器(series elastic actuator,SEA)作为典型的被动型柔顺驱动器,通过在驱动端和负载端之间串联恒定刚度的弹性元件使机器人关节获得柔顺性[5]。该类驱动器具有较低的输出阻抗及较好的力控制性能,但其控制带宽和对不同工况的适应性因刚度恒定而受到限制[6]。
为弥补SEA的缺陷,学者们提出了变刚度驱动器(variable stiffness actuator,VSA)[7]。但是,VSA除了需要驱动关节运动的电机外,还需要额外的电机来调节关节刚度,以至于其结构复杂、能耗增加[8]。同时,由于VSA刚度调节与负载变化之间的非耦合关系,在特定工况下,刚度与负载间可能会匹配不合理,例如在需要承受大负载时匹配低刚度会导致关节失稳[9]。另外,VSA刚度的调节速度受限于控制效率和电机等的响应速度,这在一定程度上会削弱人机交互的安全性。
实际上,从生物力学角度来看,人体关节周边肌肉组织的刚度与其被拉伸的程度呈非线性关系[10],这种关系可以总结为“大负载下采用大刚度,小负载下采用小刚度”。从实际应用角度来看,这种刚度选择机制具有较强的合理性:当负载较大时,为保证运动精度和控制带宽,驱动器需要较大的刚度;当负载较小时,为保证力/力矩分辨率,提高对环境感知的灵敏度,应采用小刚度以使驱动器产生足够的形变,从而便于检测[11-12]。非线性刚度驱动器(nonlinear stiffness actuator,NSA)正是基于这种自然界的刚度选择机制来设计的,利用负载与刚度之间的非线性耦合关系,根据负载大小自动调节驱动器刚度,从而不需要额外的调节刚度的电机。目前,国外很多学者已针对NSA开展了相关研究。例如:高丽大学的Park等人[13]设计了一款基于弹簧和双滑块机构的非线性刚度装置,其刚度在负载大于安全值之后骤降,以实现安全碰撞,但这会使机构难以承受较大的负载,且在刚度调节过程中机构的转角(以下简称为“刚度调节角度”)较大(40°),不适用于对运动精度要求较高的场合;意大利技术研究院的Thorson等人[14]利用内摆线机构和拉簧设计了非线性刚度装置,用于机器人在跳跃过程中的缓冲和储能,但其力矩—转角关系曲线局限于近似二次函数与近似线性函数之间,且综合尺寸较大;得克萨斯大学的Kuo等人[15]设计的柔顺机械手关节是采用滑轮组扭转压迫张紧的特殊柔性材料,以模仿人手部关节的柔性,该柔顺机械手关节的刚度曲线呈双重指数函数型,但其承载能力较弱,且对材料的要求较高。目前,大部分非线性刚度装置存在刚度调节角度过大、结构紧凑性低及刚度曲线类型单一等问题[16-18]。
为此,笔者拟基于“大负载下采用大刚度,小负载下采用小刚度”的刚度选择机制,设计一种新的非线性刚度柔顺驱动器,采用“凸轮+扭簧”机构结合齿轮的紧凑设计,实现可选刚度特性曲线的函数类型无特殊限制,且刚度调节角度较小。首先,介绍非线性刚度机构的工作原理、凸轮有效轮廓曲线的计算方法以及非线性刚度柔顺驱动器的工作原理;其次,针对所设计的驱动器样机,通过力学仿真和试验对其刚度特性进行评估,并与相近的驱动器进行对比;最后,利用具有不同峰值和频率的正弦力矩信号跟踪试验对驱动器的控制性能进行评估。
1 非线性刚度柔顺驱动器的设计方案
1.1 非线性刚度机构的工作原理
如图1所示,采用“凸轮+扭簧”机构实现非线性刚度。该机构工作原理为:滚子在驱动力矩T1的作用下绕O1旋转,并推动凸轮绕O2旋转;扭簧的一端与凸轮相连,另一端与机架相连,其中心与凸轮旋转中心重合,凸轮旋转迫使扭簧扭转,扭簧对凸轮产生阻力矩T2,使系统达到平衡状态。在该过程中,凸轮的有效轮廓直接影响滚子与凸轮之间的传动比及其相互作用力的方向,进而影响滚子的旋转角度θr。因此,可通过设计凸轮的有效轮廓曲线,实现给定的力矩—转角关系,即实现刚度的非线性变化。
1.2 凸轮有效轮廓曲线的计算方法

图1 “凸轮+扭簧”非线性刚度机构示意Fig.1 Diagram of"cam+torsion spring"nonlinear stiffness mechanism
如图1所示,点P是滚子与凸轮的接触点,也是凸轮有效轮廓曲线上的点。在凸轮旋转中心处分别建立惯性坐标系O2-xy和凸轮坐标系O2-x0y0。根据“反转法”原理[19],若能求得在任意凸轮转角θc下点P在坐标系O2-xy中的坐标(xP,yP),结合式(1)则可得到点P在坐标系O2-x0y0中的坐标(x0P,y0P),进而可以拟合出凸轮有效轮廓曲线。

根据图1所示的几何关系,可得:

式中:l、r分别为滚子绕O1的旋转半径和滚子的半径;d、e分别为O1相对于O2的水平距离和竖直距离;α为滚子和凸轮间相互作用力与水平方向的夹角。
在实际计算过程中,l、r、d和e是预设的尺寸参数,可视为已知量。结合式(1)和式(2)可知,求解凸轮轮廓点坐标时须先得到θc与θr的对应关系。
首先,对“凸轮+扭簧”机构进行静力学分析,在平衡状态下,可得:

式中:F1、F2分别为凸轮对滚子的作用力和反作用力;a、b分别为F1相对于O1的力臂和F2相对于O2的力臂;T1、T2分别为滚子的驱动力矩和凸轮受到的阻力矩。
在式(3)中,T1是关于θr的显函数,根据给定的力矩—转角关系曲线进行计算;T2根据扭簧的弹性系数K和凸轮转角θc进行计算,T2=Kθc;a、b则根据图1所示的几何关系进行计算。

联立式(2)至式(4)可得:

式(5)包含3个变量:θr、θc和α,其中α不仅会对滚子和凸轮的受力情况产生影响,而且会对其传动规律产生影响。因此,为求出θc与θr的关系,还应从传动的角度建立α、θc与θr的对应关系。
根据滚子与凸轮的传动关系,可得:

式中:μr为滚子与凸轮之间的瞬时传动比,可以根据“瞬心法”进行计算。

联立式(4)和式(7),可得:
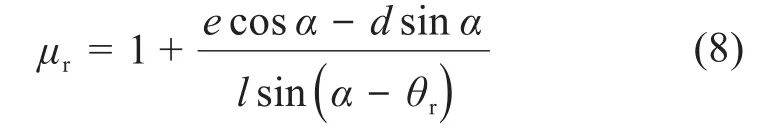
由式(8)可知,式(6)包含θr和α两个变量,它们之间存在一定的耦合关系,但无法直接求出显式解,因此无法直接对式(6)进行积分运算。为此,采用离散化方法,将θr均匀分割化成m+1段,即式(6)可以离散为:

综合式(5)、式(8)和式(9),可以计算传动过程中各离散点处的θc和α,从而获得α、θc与θr的对应关系。
结合式(1)和式(2),可求解出凸轮的有效轮廓曲线,相关计算流程如下:
1)初始化θr0、θc0、α0和迭代次数m;
2)按i从0至m依次取整数值循环进行以下步骤①至④的计算:
①将θri、αi和θci先后代入式(2)和式(1)求得轮廓点P0i;
②将θri和αi代入式(8)求得μri;
③将θci和μri代入式(9)求得θc(i+1);
④将θc(i+1)和θr(i+1)=θri+Δθr代入式(5)求得αi+1。
由上述流程可知,在计算凸轮的有效轮廓曲线时,须先确定各变量的初始值θr0、θc0、α0和迭代次数m。在运算过程中,迭代次数决定了求解精度,理论上m越大,求解精度越高,但求解时间会增加,因此m的值须根据实际情况选取。显然,在运动的初始位置处,θr0和θc0均为0°,而α0取决于驱动器的初始刚度,即给定的力矩—转角关系曲线起始点处的斜率。当驱动器的初始刚度为0 N⋅m/°时,滚子在初始位置处的运动方向应与凸轮轮廓切线的方向平行,即α0=0°,此时滚子的转动几乎不受阻碍;当驱动器的初始刚度不为0 N⋅m/°时,由式(5)、式(6)和式(8)可推导得到T1关于θr和α的显式表达式。将T1对θr求导可得:

在初始位置处,θr0=θc0=0°,将其代入式(10)即可求得α0。
1.3 非线性刚度机构预设参数的优化选择
在求解凸轮有效轮廓曲线的过程中,尺寸参数l、r、d、e以及扭簧弹性系数K是需要预先设定的,它们取值的不同会导致凸轮有效轮廓曲线求解结果的不同,因此需要根据一定的标准进行优化选择。为保证驱动器输出端的运动精度,滚子的旋转角度θr应较小,即凸轮的有效轮廓长度较短,但由于加工精度的影响,过短的凸轮有效轮廓长度会产生较大的相对误差,影响驱动器的刚度曲线拟合精度。因此,在一定的约束条件下,以凸轮的有效轮廓长度(由相邻轮廓点之间的距离之和代替)最长为优化目标,对非线性刚度机构的预设参数进行优化选择。其中,约束条件包括驱动器整体尺寸的限制以及避免产生机械干涉。上述优化问题的数学模型如下:

式中:S为凸轮有效轮廓的长度;l、d、e的上下限可以根据驱动器整体尺寸的限制及避免产生机械干涉等要求进行选择;由于滚子及扭簧采用的是工业系列产品,因此r和K应取系列值,在实际计算中可先将其取值范围设为连续区间,然后根据计算结果选取最接近的系列值。
式(11)所示优化问题属于多元约束优化问题,可用MATLAB软件优化工具箱中的fmincon函数进行求解。
1.4 非线性刚度柔顺驱动器的工作原理
图1所示的“凸轮+扭簧”非线性刚度机构仅在单方向上具有所需的刚度特性。为了使驱动器可承载不同方向的外负载,同时使其内部整体受力均匀,设计了采用具有对称结构的双向非线性刚度机构的驱动器,如图2所示。

图2 采用双向非线性刚度机构的驱动器的平面示意图Fig.2 Plane schematic diagram of actuator with bidirectional nonlinear stiffness mechanism
双向非线性刚度机构的4个凸轮(C1、C2、C3和C4)和2个滚子(R1和R2)均对称分布,相邻的凸轮共用1个滚子。为了节省驱动器外围空间,增强紧凑性,将安装在凸轮旋转中心处的扭簧转移到驱动器的中心位置处。同时,利用齿轮的传动,使4个凸轮共用1个扭簧,避免了因使用4个扭簧而可能带来的性能偏差。此外,通过齿轮传动还可以增大扭簧的转角,减小间隙误差的影响。周边齿轮和中心齿轮均采用残缺齿设计方式,并配以限位钉和弹性系数较小的止动拉簧,以保证当其中一对周边齿轮处于正常工作状态(如图2(b)中的G1和G3,负责传递扭矩),另一对周边齿轮处于非工作状态而位于固定位置处(如图2(b)中的G2和G4)时,不对正常工作的构件造成运动干扰,即拉簧仅须克服周边齿轮和凸轮自身的惯性力矩,该力矩相比于中心扭簧产生的力矩和外负载力矩可以忽略不计。
基于双向非线性刚度机构对驱动器进行方案设计,主要构件在驱动器中的安装位置如下:滚子的转轴安装在蜗轮上;凸轮与周边齿轮固连,且其转轴通过轴承安装在驱动器的输出端;凸轮的限位钉也固定安装在驱动器输出端;中心齿轮与蜗轮和驱动器输出端拥有共同的旋转中心,但彼此均无固连关系;中心扭簧的一端与中心齿轮相连,另一端与驱动器输出端相连。驱动器的工作原理是:电机通过蜗杆蜗轮驱动滚子带着双向非线性刚度机构及驱动器输出端旋转,当驱动器输出端遇外负载时,双向非线性刚度机构产生随滚子转角非线性变化的平衡力矩,从而使驱动器表现为非线性刚度。
相较于图1所示的单向非线性刚度机构,双向非线性刚度机构的构型发生了变化。为了计算该机构中凸轮的有效轮廓曲线,须对扭簧的弹性系数K和驱动力矩T1进行等效换算。设从周边齿轮到中心齿轮的传动比为μg,中心扭簧的弹性系数为Ks,则可得到中心扭簧的扭转角θs和扭矩Ts分别为:

由于中心扭簧的扭矩是通过中心齿轮均匀施加到周边齿轮,则:

结合式(12)至式(14)及T2=Kθc,可推导得到扭簧弹性系数K可等效换算为:

设驱动器的整体驱动力矩为Td,该力矩由2个对称的滚子共同传递给输出端,则:

2 非线性刚度柔顺驱动器样机设计
基于上文的设计方案,设计了“大负载下采用大刚度,小负载下采用小刚度”的非线性刚度柔顺驱动器样机,其结构如图3所示。
由图3可知,非线性刚度柔顺驱动器样机的机械结构主要由驱动端、双向非线性刚度机构以及输出端三大部分组成。其中:驱动端包括电机基座、直流电机(型号为Maxon RE40)和蜗轮蜗杆减速器(减速比为150∶1);输出端为双向非线性刚度机构除滚子外的部件提供安装位置,并为驱动器外接构件提供了接口。
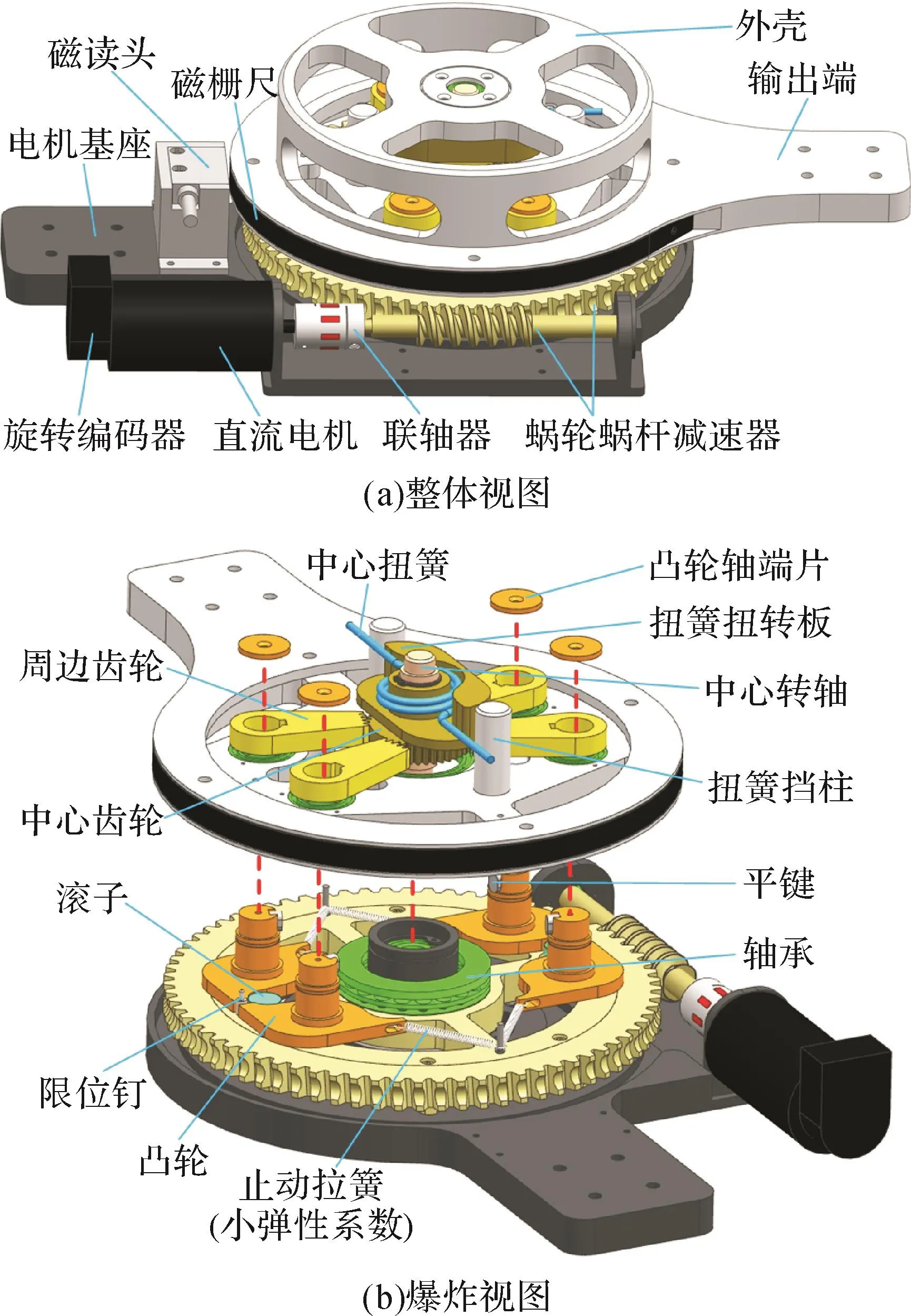
图3 非线性刚度柔顺驱动器样机的三维模型Fig.3 Three-dimendional model of nonlinear stiffness compliant actuator prototype
为了便于控制非线性刚度柔顺驱动器,须实时获得其输出端的位置信息和负载力大小。其中,位置可以通过驱动器输出端的绝对转角θa表征,负载力大小可以基于滚子的旋转角度θr(非线性刚度机构的变形量),通过对照力矩—转角关系曲线获得。在非线性刚度柔顺驱动器直流电机的尾部安装旋转编码器(型号为HEDS-5540),用于测量电机输出轴的转角θm,同时采用磁栅尺传感器(型号为MSR 500)测量驱动器输出端的旋转位移并结合圆周半径计算输出端的绝对转角θa。其中,磁栅尺传感器包括安装在驱动器输出端外圆轮廓上的磁栅尺和安装在电机基座上的磁读头,具有成本低、灵敏度高的优点。根据传动关系,由公式θr=θm/150-θa计算得到滚子的旋转角度θr。
3 非线性刚度柔顺驱动器的性能评估
为了对基于给定非线性刚度的柔顺驱动器进行性能评估,分别对驱动器的刚度特性进行仿真分析和试验验证,同时对驱动器的力矩控制性能进行试验评估。
3.1 非线性刚度柔顺驱动器刚度特性评估
3.1.1 仿真分析
预设的非线性刚度特性曲线(力矩—转角关系曲线)方程为:

柔性驱动器中非线性刚度机构的预设参数如表1所示。将其代入1.2节所述的凸轮有效轮廓曲线的计算流程中,利用MATLAB R2015b软件求解凸轮的有效轮廓曲线,结果如图4所示。依据计算得到的凸轮轮廓曲线,利用UG NX10.0建立凸轮及其对应的驱动器的三维模型,再将模型导入ADAMS 2016软件进行力学仿真,根据仿真结果绘制刚度特性曲线,如图5所示。结果表明,仿真值与理论值基本吻合,两者的平均相对误差仅为0.24 N⋅m。考虑到止动拉簧客观上会增加一定的阻力矩,这种误差是合理且可接受的。

表1 非线性刚度机构的预设参数Table 1 Preset parameters of non-linear stiffness mechanism

图4 凸轮有效轮廓曲线求解结果Fig.4 Solution of the effective profile curve of cam
3.1.2 实验分析
非线性刚度柔顺驱动器实物如图6所示。在试验中,除了在电机尾部安装旋转编码器和磁栅尺传感器用于测量角度外,还采用力矩传感器(型号为ZNNT-30NM)用于测量外负载力矩。驱动器输出端外壳是通过3D打印制成的,无法承受较大的力矩,因此将力矩传感器安装在强度较高的电机基座底部中心位置处。

图5 非线性刚度柔顺驱动器刚度特性曲线对比Fig.5 Comparison of stiffness characteristic curves of nonlinear stiffness compliant actuator

图6 非线性刚度柔顺驱动器实物图Fig.6 Physical picture of nonlinear stiffness compliant actuator
非线性刚度柔顺驱动器试验平台的信号传递如图7所示。电机尾部旋转编码器及磁栅尺传感器的信号经DSP(digital signal processing,数字信号处理)板卡(型号为TMS320F28335)接收并处理后传输给ESCON电机驱动器,并由该驱动器发送PWM(pulse width modulation,脉冲宽度调制)信号以驱动电机。数据采集卡(型号MPS-010602)采集旋转编码器、磁栅尺传感器及力矩传感器的信号并发送给PC(personal computer,个人计算机),用于数据分析和处理。
根据试验结果绘制刚度特性曲线,并与仿真结果、预设的刚度特性曲线进行对比,如图5所示。结果表明:试验值与理论值也较为接近,两者的平均相对误差为0.7 N⋅m,大于仿真值的误差,这与止动拉簧的细微影响、摩擦力及加工装配误差有关。
3.1.3 相近驱动器的刚度特性对比
为了进一步验证所设计的非线性刚度柔顺驱动器的刚度特性,选取具有与“大负载下采用大刚度,小负载下采用小刚度”类似的刚度特性,且采用“非线性传动+线性弹性元件”方式的转动关节驱动器——HypoSEA(hypocycloid series elastic actuator,内摆线串联弹性驱动器)[14]和 PVEJ(passive visco elastic joint,被动黏弹性关节)[17],进行刚度等特性参数对比,结果如表2所示。
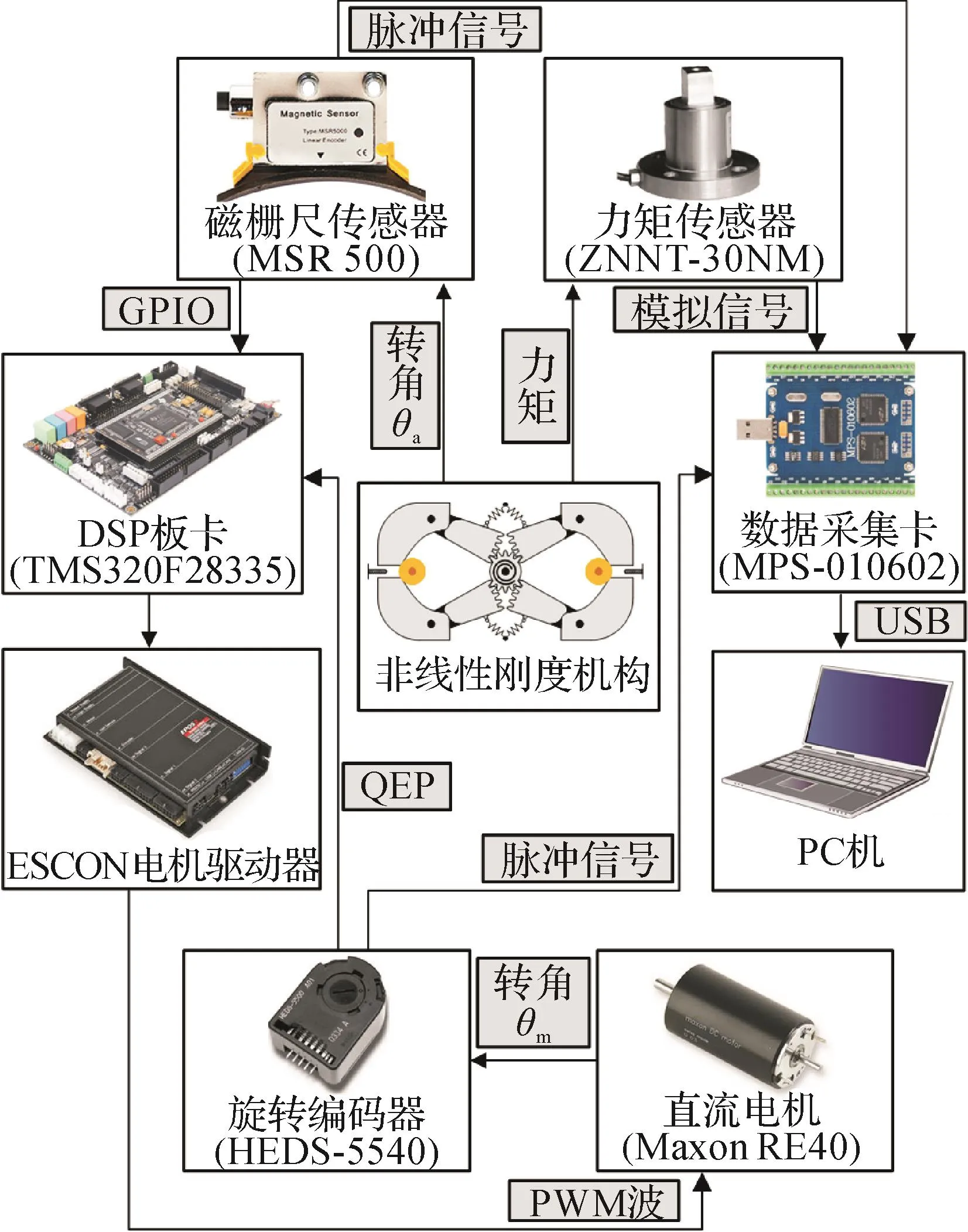
图7 非线性刚度柔顺驱动器试验平台信号传递示意Fig.7 Signal transmission diagram of nonlinear stiffness compliant actuator experimental platform

表2 不同驱动器的特性参数对比Table 2 Comparison of characteristic parameters of different actuators
由表2可知:在整体尺寸和质量方面,本文NSA处于HypoSEA和PVEJ的中间水平;在负载能力方面,本文NSA可承受的峰值力矩与PVEJ相近,但均小于HypoSEA,这是因为HypoSEA常用于跳跃机器人的腿部关节部位,需承受的冲击负载比在一般的交互场景(如正常行走)大;在刚度调节能力方面,本文NSA在具有较大的刚度范围的同时具有较小的刚度调节角度范围,这说明本文NSA的刚度调节更灵敏,可保证驱动器具有更好的运动精度;在刚度曲线拟合误差方面,本文NSA的刚度曲线拟合误差最小,HypoSEA的刚度曲线拟合误差最大可达到约80%,PVEJ的刚度曲线拟合误差为3%~50%[17],这表明本文NSA的精度更高。由此可知,本文所设计的非线性刚度柔顺驱动器的综合特性较优。
3.2 驱动器控制性能评估试验
力矩控制是人机交互设计中的重要环节,对期望动态力矩的跟踪效果可以反映驱动器的力矩控制性能。以正弦波作为期望信号进行力矩跟踪试验,选择力矩峰值(2和8 N⋅m)和频率(1和1/3 Hz)不同的正弦信号进行对照,跟踪时间持续9 s,结果如图8所示。

图8 驱动器正弦力矩跟踪试验结果Fig.8 Experimental results of sinusoidal torque tracking for actuator
图8所示结果表明,整体上各组试验的力矩响应值与期望值都较为吻合,响应值与期望值之间存在细微的相位迟滞,且程度有所不同。对比图8(a)和图8(b)发现,频率大的信号比频率小的信号相位迟滞更明显,即频率比越大,相位延迟越大;对比图8(b)和图8(c)发现,期望信号的峰值越大,相位迟滞现象越不明显,这是因为所设计的非线性刚度柔顺驱动器的刚度是随负载增大而增大的,即力矩信号峰值越大则刚度越大,响应越迅速。综合来看,在信号力矩峰值和频率不同的条件下,非线性刚度柔顺驱动器的力矩跟踪的相位迟滞现象虽存在但均不明显,由此可证明本文所设计的非线性刚度柔顺驱动器具有良好的力矩控制性能。
4 结论
1)针对人机交互安全性和自然交互特性,基于“大负载下采用大刚度,小负载下采用小刚度”的刚度选择机制,设计了一种新的非线性刚度柔顺驱动器,利用“凸轮+扭簧”机构结合齿轮传动,可实现双向对称非线性刚度。
2)通过仿真和试验可知,该驱动器具有较好的刚度特性,可按给定的非线性刚度特性曲线进行刚度调节。
3)从尺寸、质量、负载能力、刚度调节角度、刚度范围和刚度曲线拟合精度等方面与相近的驱动器进行了比较,结果表明所设计的非线性刚度柔顺驱动器具有优良的综合特性。
4)通过试验测试了非线性刚度柔顺驱动器对力矩峰值和频率不同的正弦力矩信号的跟踪效果。结果显示,虽然存在细微的相位迟滞现象,但驱动器对不同力矩信号的整体跟踪效果良好,初步证明了所设计的非线性刚度柔顺驱动器具有良好的力矩控制性能。

