云计算中高效可即时撤销的无证书签名方案

刘 艳，王 丹+，汪祖民，段 茹

(1.大连大学 大连市环境感知与智能控制重点实验室，辽宁 大连 116622；2.大连大学 信息工程学院，辽宁 大连 116622)

0 引 言

随着社会的进步和科技的不断发展，可穿戴可植入等监测小型设备在给人们带来高质量医疗服务的同时，也存在传输过程中身份数据信息被泄露及非法篡改的危险。数字签名[1]可以有效地解决数据在传输过程中的完整性问题，以及确定是合法用户传输。传统的公钥密码学存在着复杂证书管理问题。身份加密的签名机制[2-6]仍存在密钥托管问题，且无法抵抗恶意的KGC攻击。无证书签名方案被提出[7]，但没有进行安全性证明。近年来，无证书签名方案被广泛研究，但存在着一定的安全漏洞。其中，撤销机制的提出是解决签名安全问题的主要方法。文献[8]和文献[9]都采用半可信的安全媒介(security mediator, SEM)实现签名的撤销，但增加了系统的不安全因素。随后，基于时间密钥的可撤销无证书签名方案被提出[10-13]，在这些方案中，都存在用户私密信息泄露的危险。同时，方案采用大量的双线性对运算，增加系统的计算代价，不适用于云环境中资源受限的小型设备。

为此，本文方案采用椭圆曲线签名算法代替双线性对算法，在保证安全性的基础上降低了计算复杂度。KGC维护一个撤销时间表，当检测到用户密钥泄漏或过期时，KGC立即给所有未被撤销的用户更新最新时刻的时间密钥，已撤销的用户无法获取新时刻下的时间密钥，签名验证不成功，从而实现签名的即时撤销，并在随机语言模型下证明安全性。

1 基础知识

1.1 椭圆曲线加密

椭圆曲线的曲线方程与计算椭圆周长的方程相似。一般椭圆曲线方程形式即y2=x3+ax3+bx2+cx+d， 它是由方程全部解 (x,y) 加上一个无穷远点O构成的一个集合。椭圆曲线离散对数解的困难性(ECDLP)定义请参见文献[14]。

1.2 无证书签名方案的定义

无证书签名方案算法构成如下：

(1)系统建立：输入安全参数k，返回系统公共参数params及系统主密钥s，建立一个无证书系统，同时s由KGC秘密地保存。

(2)秘密值生成：随机选取该用户的秘密值xID。

(3)部分密钥生成：此算法是KGC利用已知用户的身份标识ID，系统公共参数params，系统主密钥，生成用户的部分私钥dID，并通过公共信道发给相应的用户，由用户保存。

(4)用户私钥生成：输入系统公共参数params，用户的身份标识ID，部分私钥dID和秘密值xID，输出该用户的完整私钥SKID。

(5)用户公钥生成：输入用户的身份标识ID，系统公共参数params、部分私钥dID和秘密值xID，生成用户的公钥PKID。

(6)签名：输入用户身份标识ID、系统参数params、待签名消息m、公钥PKID以及用户私钥SKID，执行签名算法生成签名σ。

(7)验证：验证者输入系统安全参数params、身份为ID的签名者、用户公钥PKID以及消息m，对签名σ进行有效性验证。若通过验证，则返回“1”，否则，返回“0”。

2 方案的具体构造

本文以老年居家无线远程医疗监护系统为例阐述方案的具体构造，如图1所示。

图1 系统模型

用户代表病人及患者，用户将数据发送给医疗客户端，需要双方进行身份的认证，确定用户身份的合法性以及发送信息的完整性。KGC分别向用户与远程客户端发送部分私钥进行签名的认证，KGC一般是由半可信的盈利组织担任，存在KGC系统因为牟利伪造合法用户身份的弊端。远程医疗端一般是由医院等医疗服务中心担任，用户及医疗客户端签名认证成功后，医疗客户端提供相关医疗服务。

本文方案在传统无证书签名方案的基础上，采用椭圆曲线加密算法进行完整的签名。由KGC新生成时间密钥，并维护一个撤销时间表，见表1。

表1 即时撤销过程

当检测到用户身份过期或私钥泄露时，KGC给所有未被撤销的用户更新最新时刻t2的时间密钥st2，已撤销的用户还停留在t1时刻的时间密钥st1，无法得到最新的时间密钥，签名验证不成功，从而实现签名的即时撤销性。方案的具体构造为：

(1)建立系统：KGC选择安全参数k，选取有限域为Fq(q为大于3的素数)的椭圆曲线E∶y2=x3+ax+b， 基点为G，P是G的一个生成元，s是系统主密钥，并由KGC秘密保存s。KGC计算系统公钥Ppub=s·P， KGC选择两个免碰撞的哈希函数：H1、H2。其中

KGC公布系统参数如下

params={q,G,P,Ppub,H1,H2,H3}

(2)生成秘密值：由身份为IDi的用户随机选取秘密值xi作为组成签名私钥的一部分。

(4)生成用户公钥：用户计算PKi=xi·P, 并把PKi作为用户的公钥。

Ri=ri·P

(1)

h′i=(IDi,Ri,Ppub,t)

(2)

st=ri+h′i·s

(3)

其中，t是系统初始时间。将时间密钥(Ri,st)通过公共信道发送给用户。用户收到时间密钥(Ri,st)后验证等式stP=Ri+hi·Ppub是否成立，若成立，则接受其作为时间密钥，否则返回上级。

Ti=ti·P

(4)

σi=ti+ki·xi+di+st

(5)

其中，ki=H2(IDi,m,Ti,PKi,Ri,Ppub)， 所以签名方输出消息m的签名为 (Ri,Ti,σi)。

(7)验证签名：远程医疗客户端验证签名以确定消息发送客户端为合法客户端，需做如下操作：验证等式σi·P=Ti+ki·PKi+di+st是否成立，若等式成立，则接受该签名，否则输出⊥并返回上级。

3 方案证明

3.1 正确性

σi·P=ti·P+kixi·P+di·P+st·P=
Ti+ki·PKi+2ri·P+his·P+h′is·P=
Ti+kiPKi+2Ri+hiPpub+h′iPpub

可得出等式左右两边相等，则证明本撤销签名方案是正确的。

3.2 安全性

一般的无证书签名系统，通常可划分为两类：第一类是恶意不诚实的用户，第二类是恶意但诚实的KGC，具体描述如下：

类型一敌手：A1可以替换任意用户公钥，但其不知道系统的主密钥与用户的部分私钥。

类型二敌手：A2不能替换任意用户的公钥，但其掌握了系统主密钥和用户的私钥。

考虑到已撤销的用户仍可对密钥进行攻击，本文增设类型三敌手，即已撤销的用户：A3无法获得新的时间密钥，但可以替换用户攻击。

随机预言模型中，攻击者1、2类型[10-13]中已有许多详细的证明，此处不再阐述，本文通过如下证明验证攻击类型3的安全性。

证明：假定给算法S一个ECDLP的实例，给定{P,aP}，利用S解决ECDLP问题。设Ppub=aP， 其中，a是系统主密钥，A3是攻击者，即已撤销的用户，知道用户的秘密值和部分私钥。S维护列表L1,L2,Ld,Lt,LPK， 初始状态下列表为空。A3可以执行以下询问：

H1询问：收到A对 {IDi,PKi,di,hi} 的列表L1询问后，B执行以下操作：

(1)若表L1中存在 {IDi,PKi,di,hi}， 则返回hi给A3。

H2询问：收到A3对 {IDi,PKi,Ri,ki} 的H2询问后，S进行以下操作：

(1)若列表L2中存在 {IDi,PKi,Ri,ki}， 则返回ki给A3。

部分私钥询问：收到A3对 {IDi,PKi} 的列表Ld询问之后，S执行以下操作：

(1)当列表Ld中存在 {IDi,PKi,Ri,di}， 则返回 {di,Ri} 给A3；

时间密钥询问：收到A3对 {IDi,PKi,t} 的列表Lt询问后，S执行以下操作：

用户公钥询问：收到A3对IDi的公钥询问后，S执行以下操作：

签名询问：收到A3对 {IDi,m} 的列表LS询问，S执行以下操作：

(2)若 (IDi,t)=(ID*,t*) 或公钥已经被替换，S失败并终止游戏。

σiP=Ti+kiPKi+2Ri+hiPpub+h′iPpub

(6)

σi1P=Ti1+ki1PKi+2Ri+hiPpub+h′iPpub

(7)

(8)

可知上述等式中有3个未知数σ,Ti,ki， 联立式(6)～式(8)，可求解出来这3个未知数，从而解决椭圆曲线离散对数问题。

4 方案评估

4.1 效率评估

为方便接下来的评估，定义S表示一个标量乘运算，P表示一个双线性对运算，H表示一个散列运算。M代表一个点乘运算。本方案与满足签名的可撤销性，且具有高安全性的文献[10]与文献[12]进行的效率对比分析见表2。

表2 效率对比

双线性对运算P分别是标量乘S、点乘运算M与散列函数运算H的21倍[15]。因此，由表2可知，本文方案等同于进行了7次标量乘运算，而文献[10]相当于进行70次标量乘运算，文献[12]相当于进行了111次标量乘运算，本方案签名效率明显提高。

4.2 运算复杂度评估

设模乘运算的数据规模是n，一次双线性对运算的运算复杂度是O(21n2)，一次标量乘及点乘的运算复杂度是O(n2log2n)，本文方案计算复杂度为7n2log2n，而文献[10]、文献[12]则包含了较多运算，计算复杂度分别为(7log2n+63)n2、(6log2n+105)n2。如图2为在相同数据规模下3种方案运算复杂度对比，当n为10×105时，文献[10]和文献[12]的方案签名复杂度分别为2×1014与2.2×1014，本方案复杂度为1×1014，签名复杂度相比文献[10]、文献[12]分别提高了50%与45.5%。

图2 签名复杂度对比

5 实验验证与分析

实验平台采用Windows10、i7处理器模拟医疗云客户端与云端硬件环境对数据进行签名与验证操作，客户端使用JDK1.8对医疗数据进行签名与验证。对于椭圆曲线签名算法，为了达到其安全级别，选择椭圆曲线标准推荐的有限域为P,素数域为256 bit的椭圆曲线方程，即：y2=x3+ax+b， 其中P=FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFFa=FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFCb=28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93为了真实模拟中小型手腕佩戴式数据采集设备与医疗云之间信息传输的签名过程，本文对UCI数据库(University of California Irvine，UCI)真实数据集中小型设备采集的一段数据进行签名。数据M为 {"ID":"0005","age":"45",:"gender":"girl","heartBeat":"80","bloodPressure":"140/100","step":"5000","time":"2006-03-24"}。 控制主机需要对采集的数据进行签名操作，云端对签名进行验签操作，签名生成阶段与验证阶段的仿真如图3和图4所示。

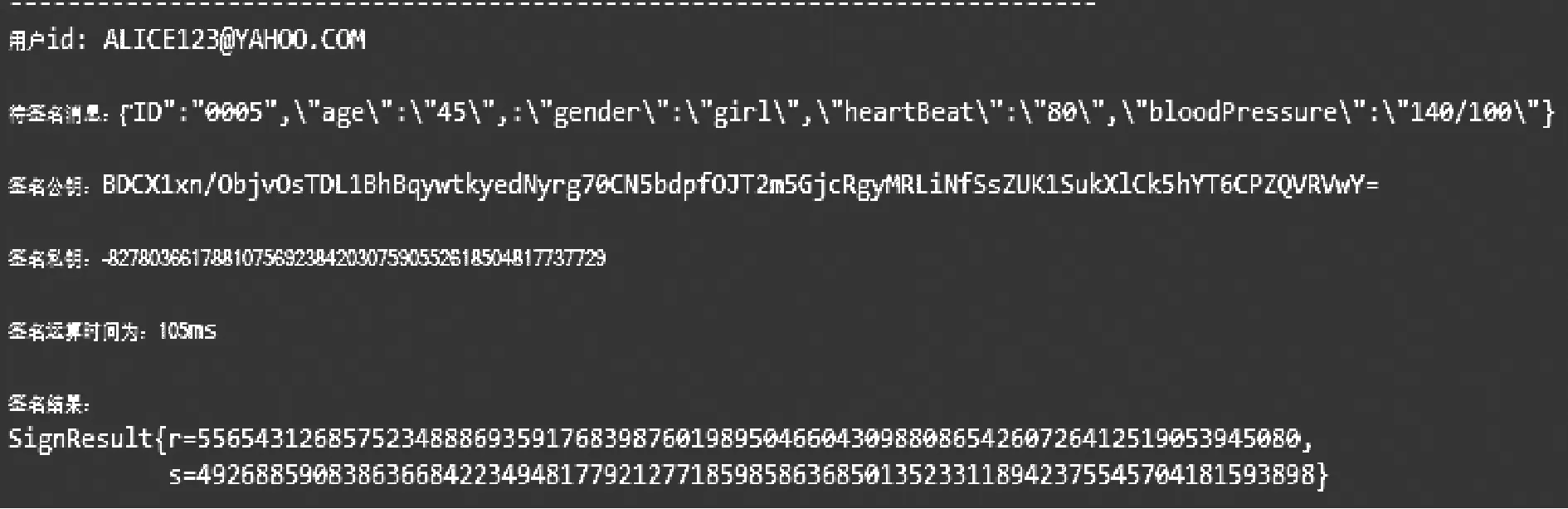
图3 签名生成阶段结果

图4 验证生成阶段结果

用户对消息M进行签名，签名及验证过程所用时间分别为0.105 s和0.008 s，以方案运行50次的平均签名时间为基准进行对比，本文方案平均总签名耗时0.11 s，文献[10]和文献[12]平均总耗时分别为0.156 s和0.166 s，本文签名方案用时更短，适用于当前云环境下的签名方案。

6 结束语

本文提出了一种基于椭圆曲线加密算法的无证书签名方案，即时更新密钥技术的引入有效解决了用户因撤销不即时导致的隐私泄露。KGC维护一个时间撤销表，密钥泄露或身份过期的用户获取不到最新的时间密钥，避免了恶意第三方伪造成合法用户，并已在随机预言模型下证明其具有抗签名密钥泄露的安全性。本方案签名用时时间为113 ms，比现有方案缩短了50 ms左右，更适合于当前云环境下资源受限的小型设备。