基于密度划分的数据存储方法与技术

赵会群，李春良

(北方工业大学 计算机学院，北京 100144)

0 引 言

在传统的数据压缩研究领域中，依据压缩处理后数据是否可以完全恢复，将压缩算法分为无损与有损压缩两种方式[1]。无损压缩又大体分为以LZW为代表的基于字典结构的压缩算法[2-6]和以Huffman编码为代表的基于统计的压缩算法[8,9]。无论是LZW还是Huffman编码在实际操作中都存在较大局限性，如LZW局限于原始数据集中重复字符或字符串出现的次数，数据字典结构的大小等。从去除数据源中重复信息的角度来说，LZW与Huffman的处理角度都是筛选出数据源中重复字符(字符串)进行擦除降低冗余度操作，而在数据源中，由重复字符串及相同信息含义的重传数据所组成的密集信息区域，针对此种情况，本文开辟新的思路，参考挖掘中的聚类思想[10]，根据密度分散的不同进行有效划分，提出数据源中的密集信息区域，并对其进行统一擦除操作，去除其中具有重复属性的数据，只保留可以描述当时原高密度区域“场景”信息的少量数据，以达到数据压缩的目的。

1 密度区域划分算法研究

1.1 密度区域划分算法

筛选数据源高密度数据区域，其本质为是把数据源中的每一个数据视作一个数据对象，通过不断的迭代匹配将属性高度相近的对象化为到不同区域(子集)的过程。关于如何挖掘出数据中的高密度区域，在数据挖掘领域，有许多基于密度的数据挖掘算法可借鉴，如DBSCAN与K-means算法等[11-13]。类似于DBSCAN传统思路的聚类算法在处理数据表现疏散的数据时，其算法表现会呈现无法精准进行区域划分，划分后的区域特征呈现相近，并且在处理过程中存在无用重复操作。为了更为快捷有效划分出数据源中的高密度区域，本文借助区域面积与“浓度”的概念集合传统的聚类思想，改进算法，用数据源中单位面积内样本点的个数对数据源数据密度分布进行精准刻画，并且规避了传统做法中对每一个样本点进行便利判断的冗余操作，算法具体步骤详细介绍如下：

Input：

Data：待处理原始数据集

R：滚球半径

MinThreShold：滚球2R区域密度阈值参数

Output：高密度数据集

算法Pseudo Code：

(1)初始化数据集目标点为unvisited；

(2)初始化高密度数据集合Es；

(3)Do

(4)从unvisited数据集中随机选择数据点p，并将其属性修改为visited；

(5)计算p点2R-领域内部属性为unvisited点个数num及其构成的领域面积Area；

(6)依据num与Area值计算p点领域区域密度，p-ThreShold=num/Area；

(7)Ifp-ThreShold>=MinThreShold；

(8) 初始化包含P点R-领域属性为unvisited点的密度区域E，并将其内部点集属性修改为visited；

(9) ForEachEs密度区域E’；

(10) ForEach 密度区域E点p’；

(11) Ifp’2R-领域、E’区域存在交集；

(12) 将E、E’进行数据合并；

(13) ElseE归入Es密度区域集合中；

(14)Else

(15) 更新p点2R领域内所有p’属性为visited；

(16)Until原始数据中数据点p均为visited;

下面给出密度区域划分算法中计算区域面积Area的详细过程：①借助滚球法获取区域的边界信息(点集构成的区域边界链)；②依据获取的区域边界信息借助矢量积求解区域面积。

1.2 利用矢量积计算任意多边形面积

通常做法为先通过耳切法等[14]将不规则多边形进行三角划分，分割成n个大小各异的三角形，通过累加分割后的各个三角形的面积得到最后的多边形面积。其缺点是随着边界点的增加，会增长三角划分的复杂度，计算过程亦会非常繁琐。为了简化操作快速获取任意多边形的面积，本文采取先对多边形Ω建立矢量图，如图1所示，对相邻的两个边界点所组成的有向矢量三角形根据矢量外积计算其矢量面积，最后累加所有矢量三角形面积值，从而求出整个多边形面积。具体多边形面积计算公式推导过程请参见参考文献[15]。

图1 矢量图

1.3 滚球法求解任意多边形边界

处理求解多边形边界点问题扫描法、MelKman等算法是常用的算法，其特点是简洁快速，缺点也十分突出，其主要用来处理凸包边界点求解，而对于求解任意形状的簇包其算法表现过于粗糙，误差较大，无法取得理想边界点效果。在本文提出的算法中，精准获取区域边界链是核心问题，因此，本文提出一种获取任意簇包边界点算法：滚球法。

核心思想是用一个初始值为R的矢量圆从区域的初始点不断迭代滚动，每次滚动在区域中首次触碰的数据点视作该区域下一边界点，当矢量圆再次回到初始点时视作迭代滚动完成，该区域的边界点集由矢量圆在迭代滚动过程中触碰的所有数据点所构成。

图2 钉群

图3 边界点F

极坐标排序：对点集中的点建立以起点O和初始方向n的逆时针排序的新点集。

向量叉积：其结果可以用以描述的为两个向量的相对关系，以为向量a、b为例，计算公式为ax×bx+ay×by， 其结果的正负性质可描述为正值表示向量b位于向量a的逆向位置，负值则相反。

极坐标排序，如图4所示。

图4 极坐标排序

算法详细介绍如下：

Input：

Data：待处理数据集

R：滚圆半径

Output：区域边界链boundary

算法Pseudo Code：

(1)初始化边界链boundary；

(2)取Y轴方向最小值点p作为边界链初始点，并加入边界链boundary中；

(3)Do

(4)If boundary size 等于1

(5) 初始化边界点p点2R-领域点集E；

(6) 采用p点-X轴方向作为极坐标排序所需的基准向量，对点集E中的点进行极坐标排序；

(7) ForEach 点集E中点p’；

(8) 以pp’为弦作圆O；

(9) If 圆O点集、点集E不存在交集；

(10) 点p’作为下一边界点归入boundary中；

(11)Else boundary size 大于 1；

(12) ForEach有向边界链boundary

(13) 获取最后归入边界链boundary中的点p、p’；

(14) 初始化边界点p点2R-领域点集E；

(15) 以pp’方向为基准向量，对点集E重复(6)-(10)操作；

(16)Until无下一边界点 or 下一边界点为初始边界点p；

2 实验分析

在上文中，给出了针对降低数据冗余度，解决数据源中带有重复性质的数据比例过高的问题本文的解决方案，并给出了对应的密度区域划分算法的思想与具体步骤。下面对本文提出的算法结合具体的案例，对其实际可行性做更为详细的论证。

为了更为全面的验证其对不同数据都能实现有效的压缩存储，本文采用了GSP地理信息数据与路由表两种数据属性截然不同的数据源。GPS数据源为现实车辆行驶轨迹真实数据，其数据属性表现为会自主呈现出聚集效应，是符合本文思想的理想数据；路由数据的数据属性则会呈现出传统压缩算法更善于处理的大量重复字符(字符串)。两种数据理论都可采用本文提出的密度区域划分数据压缩策略进行高效压缩存储。

2.1 GPS数据压缩存储

本文第一个实验验证采用的是出租车车辆轨迹数据，对市区一万多辆出租车(源自微软亚洲研究院)7天的车辆行使轨迹GPS数据，以每辆车为单位，每5 s采集一次GPS地理位置信息，最终形成的车辆GPS行为轨迹信息，以时间作为横轴坐标参考，呈现出线性分布。具体数据见表1，包含了车辆的ID号(不是车牌号)、行驶的日期、时间、车辆经纬度信息。

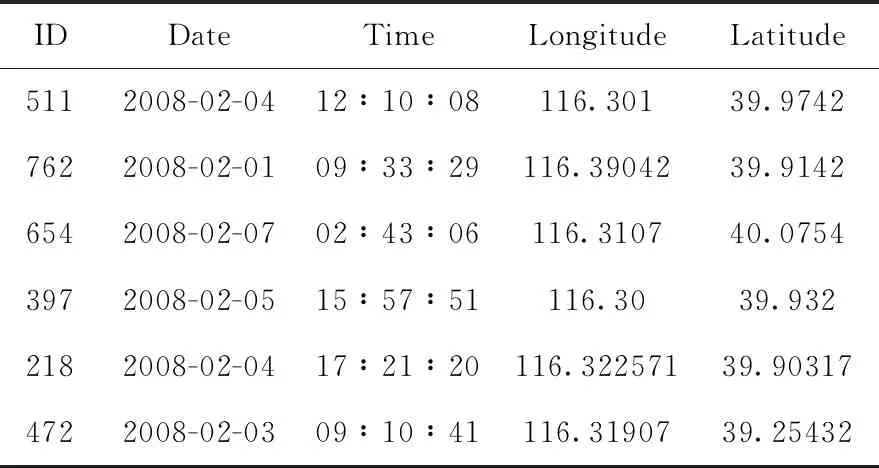
表1 车辆行驶轨迹数据字段

2.1.1 车辆轨迹GPS数据分析与压缩

按天为基本单位，使用本文密度区域划分算法对数据集做处理，将数据集中车辆GPS信息高度密集的区域从原始数据集中进行抽离，形成孤立的密集区。如图5中密集区域所示，每一个密集区其代表的是实际含义为车辆高频率聚集叠加，内部车辆轨迹信息高度重复。

图5 高密度区域

针对抽离的高密度区，内部大量重复的车辆GPS轨迹信息对描述此区域高密度特性而言是没有必要重复存储的，是对宝贵的存储空间的浪费。因此，基于本文去除密集区域重复信息的思想，对此密集区，利用本文提出的算法，只保留可以反馈密集区基本样貌信息的临界数据，舍弃内部重复叠加的车辆GPS信息，减小对存储空间的压力。如图6所示。

图6 去除重复数据

针对每一个划分出的高密度区域，只对其保存根据本文算法得到的边界链与区域中心数据，和区域内部的时间散列数据(去除内部重复GPS数据后，区域内的时间值变化失去线性规律)，基于基本统计的车辆ID信息(即车辆ID叠加重复的次数)，最终压缩处理后的数据存储格式见表2。

表2 密度区域数据样例

时间值分布，如图7所示。

图7 时间值分布

2.1.2 车辆轨迹GPS数据的恢复

数据恢复时，基于密集区高度密集特性，可采用近似于均匀分布的数据散列方式，围绕保留的区域中心，在区域边界内散列铺满整个区域，复原密集区数据样貌。具体方式，借助射线法判断复原的GPS数据是否在边界链内，利用保留的车辆ID、车辆ID叠加次数、区域内车辆部行驶时间信息，进行数据拼接，还原车辆完成轨迹GPS信息，进而真实还原整个抽离的密集区车辆信息叠加分布信息。

完整数据，如图8所示。

图8 完整数据

2.1.3 空间点与任意不规则多边形位置判定

判定点与任意不规则多边形的位置关系有多种方式，其中射线法是行为有效最为简单直接的一种校验方法。其通过将待校验的点分别向两侧做水平射线，分别判断左右射线与不规则多边形交集信息，如图9所示，两侧射线均与此多边形存在奇数个交点，则说此点位于多边形内部。

图9 射线法

2.2 路由表数据压缩存储

本文第二个实验采用美国俄勒冈大学路由查看项目部分路由数据作为数据源。

2.2.1 路由数据介绍

互联网中通信两端在进行交互时，其大概率需跨局域网进行交互，此时需要进行传输路径择优选择，路由其扮演的是跨局域网交互传输路径选择与描述角色(具体由AS自治系统(autonomous system)构成了此跨局域网传输路径)，本文采用的路由信息数据就是多个AS系统之间严格遵循网关协议连接形成的一条条路由跳转路径数据信息。数据格式见表3。

表3 路由数据

2.2.2 路由数据分析及高密度区域挖掘

采用无向图的方式将彼此存在跳转关系的AS系统进行双向连接，更为直观地展现AS系统之间的交互关系，如图10所示。

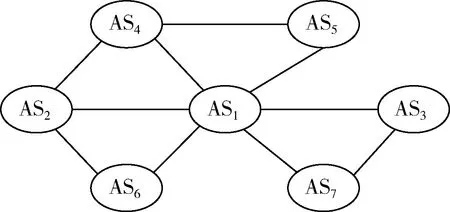
图10 AS无向图

互联网中每秒都存在着极高频率的交互动作，而AS系统是有限的，任意相邻的两个AS系统之间都在进行极高频率的重复跳转，其在数据源中的表现为某一条跳转路径以极高的频率被重复存储。以下图为例，17974-7713跳转路径存储了3503次，路径3549-3356AS跳转路径存储了403次。AS跳转路径，如图11所示。

图11 AS跳转路径

在原始数据中，以3549-3356为例，存在大量与此跳转路径具有直接交互关系的AS系统，这种高频率AS系统跳转路径的聚集现象完全符合本文去重思想，提供了可行性依据。利用本文提出的密度区域划分算法,在操作过程中，将路由数据集中的跳转路径视为一个二维点，则可将整个路由数据集视为类似车辆GPS性质的二维点集数据包，初始面积值取1，将原始数据集中大量存在的由众多高频率AS系统构成的局域高密集子网区域进行抽离。根据数据表现，每个抽离的局域高密集子网区域具备以下特点：①局域高密集子网区域AS跳转路径重复率极高；②局域高密集子网区域AS系统个数数量不高，表现为AS无向图结构不复杂；③每个AS系统编号都由16 bite组成，基于此构建的AS系统跳转路径更长。

2.2.3 路由数据高密度子网区域数据压缩存储与恢复

从数据存储的角度进行分析，针对抽离出的局域高密集子网区域中的跳转路径进行无条件完全存储，可视为是对存储空间的浪费。由于AS自治系统编号具有唯一性的特性，在对抽离出的局域高密集子网区域进行压缩存储时，其内部的AS系统编号不可直接进行模糊擦除，因此，对每一个局域高密集子网区域建立由其内部AS系统编号构建的矩阵，借用占位符的概念，利用密集区域内部跳转路径在矩阵中的位置信息进行占位替换，减小整个密集区的重新信息，减小对存储空间的压力。

采集局域高密集子网区域中的AS系统编号，进行根据编号在区域内出现的频率进行自然排序构建AS编号矩阵，在密集区域中(见表3)，对每一对跳转路径在矩阵中进行寻址，用自然数标记此跳转路径在矩阵中的位置，进行占位替换。表4为处理后的压缩文件文件。数据恢复时，构建矩阵模型，依据压缩文件中记录的占位符等信息读取在矩阵中位置信息，进行AS系统编号恢复，进而恢复整个局域高密集子网区域。

表4 压缩后的路由存储文件

2.3 性能分析

数据压缩的性能指标主要是压缩率与压缩速度，针对于本文所采用的两种测试数据集本身都不足够大的情况，这里主要讨论压缩率。压缩率的计算公式如下。在数值上，压缩率越小代表算法的压缩性能越好

对实验结果进行分析(见表5和表6)，从整体上来看，基于本文提出的数据压缩策略下的密度区域划分算法相较传统的LZW算法在压缩率上表现更好，尤其是GPS测量地理信息数据更能体现文本的思想，不仅局限于去除重复的车辆ID、日期等重复字符(字符串)，更去除了筛选出的高密度区域中具有重复属性的数据，相较之下路由表数据由于无法像GPS数据完全去除筛选出的高密度区域中重复属性数据，压缩率有所降低。结合两种数据的实验结果表明，相较于传统的数据压缩算法，本文提出的数据压缩策略对数据的灵活性更高，数据适用性更好。

表5 GPS数据

表6 路由数据

3 结束语

本文通过对现有的数据压缩存储策略的分析，提出一种基于密度区域划分，挖掘原始数据中高密度区域，去除高密度区域中包含的重复性质数据，以达到降低数据冗余度实现数据源压缩的目的。给出针对各种数据具有普适性的数据密度区域划分算法，以提取数据中的高密度区域。并选取了GPS地理信息与路由表两种数据属性完全不同数据源对本文提出的算法进行了验证。实现结果不仅验证了算法的可靠性和压缩策略的可行性与有效性，更进一步表明了本文提出的数据压缩策略相对于传统的数据压缩策略在压缩率与数据适用性上更具优势，更加灵活。