空心微瓶谐振腔的曲率模型及其传输特性研究
(上海大学 通信与信息工程学院 特种光纤与光接入网重点实验室,上海 200444)
引言
近年来,支持光学回音壁模式(whispering gallery mode,WGM)的谐振腔受到了人们的广泛关注。这些谐振腔基于全反射原理将光限制在其内部,使其具有高品质因子(quality factor,Q-factor)和小模式体积的特性[1]。WGM 谐振腔的结构主要包括微球[2-3]、微环[4]、微盘[5]和微环芯[6]等。这些类型的谐振腔主要将WGM 限制在各自的赤道面上,因此它们通常被视为二维谐振腔[7]。随后,WGM 谐振腔的研究扩展到了微瓶谐振腔。由于其自身的非球面特性,它将WGM 限制在轴向上的2个转折点之间,使其不仅支持沿赤道面环绕的径向WGM,还支持在轴向上传输的WGM[8]。这种轴向限制作用使微瓶谐振腔又被称为三维谐振腔。这种对光的三维限制能力提升了腔内的光场能量和光子寿命,因此微瓶谐振腔被广泛应用在低阈值激光器[9]、传感器[10]和腔光力学[11]等领域。
微瓶谐振腔独特的限制作用吸引了众多学者研究其传输特性[12-14]。2009年,英国南安普顿大学的G.Murugan 等通过熔接机放电并同时推进的方法制备出了微瓶谐振腔[15],分析了沿着微瓶谐振腔不同耦合位置所激发的传输谱特性。2016年,复旦大学的L.Xu 等通过引入紫外光固化胶作为损耗单元,选择性地抑制微瓶谐振腔的模式谐振,降低了微瓶谐振腔传输谱的模式密度[16]。2018年,浙江师范大学的G.Wu 等基于有限元数值分析法研究了曲率对空心微瓶谐振腔传输特性的影响[17]。文中通过控制熔接机对石英毛细管的放电次数制备出了不同曲率的空心微瓶谐振腔[18],根据理想气体状态方程推导出了曲率变化模型,并且通过实验研究了不同曲率下空心微瓶谐振腔的传输特性。
1 轴向WGM的理论仿真
微瓶谐振腔可以将WGM 限制在轴向方向上的2个转折点±Zc之间[19]。图1为微瓶谐振腔的几何结构,红线表示轴向WGM。微瓶半径R(Z)沿Z轴方向的变化情况可以通过二次谐波函数来近似[8]:
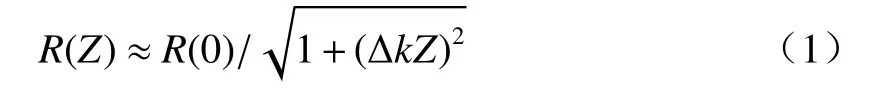
式中:Z=0,即表示在微瓶谐振腔的中心位置处,此时R(0)是微瓶谐振腔的最大半径;∆k表示微瓶谐振腔的曲率,∆k越大则意味着微瓶谐振腔的鼓起程度越大,当∆k=0时,该结构等同于微柱型谐振腔。

图1 微瓶谐振腔示意图Fig.1 Schematic of micro-bottle resonator
在Z轴方向上,电场EZ可以类比一维谐振子问题,相应的解可以表示为[19]
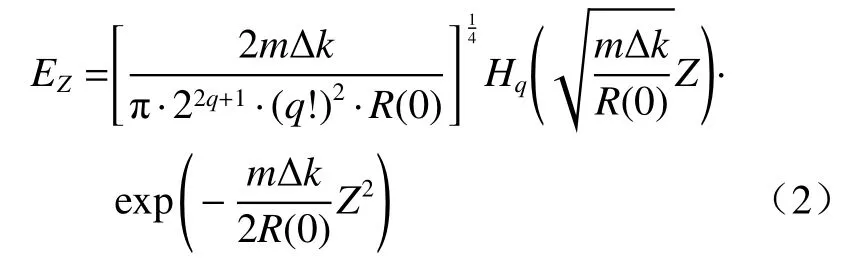
式中:m是方位角量子数;q是轴向量子数;Hq为第q阶的Hermite 多项式。
研究不同曲率下微瓶谐振腔中轴向WGM的分布情况。根据(1)式可以得到微瓶谐振腔的轮廓曲线,结果如图2(a)所示。对应的Δk分别为0.008 μm−1、0.007 μm−1、0.006 μm−1、0.005 μm−1和0.004 μm−1。随着Δk的增加,微瓶谐振腔的R(0)也随之增加。然后,将上述曲率代入到(2)式中并设置参数R(0)=70 μm,m=370,q=0,可以得到腔内WGM的光场分布情况,结果如图2(b)所示。|Ez|2表示光场的能量幅值。从图2(b)中可以观察出:随着Δk的增加,±Zc之间的距离会减小,光场幅值|Ez|2会不断增大。结果表明,曲率越大的微瓶谐振腔对光的束缚能力越强,相应的腔内能量也会越高,有助于增强光与外界物质之间的相互作用,从而实现高灵敏传感[20]。
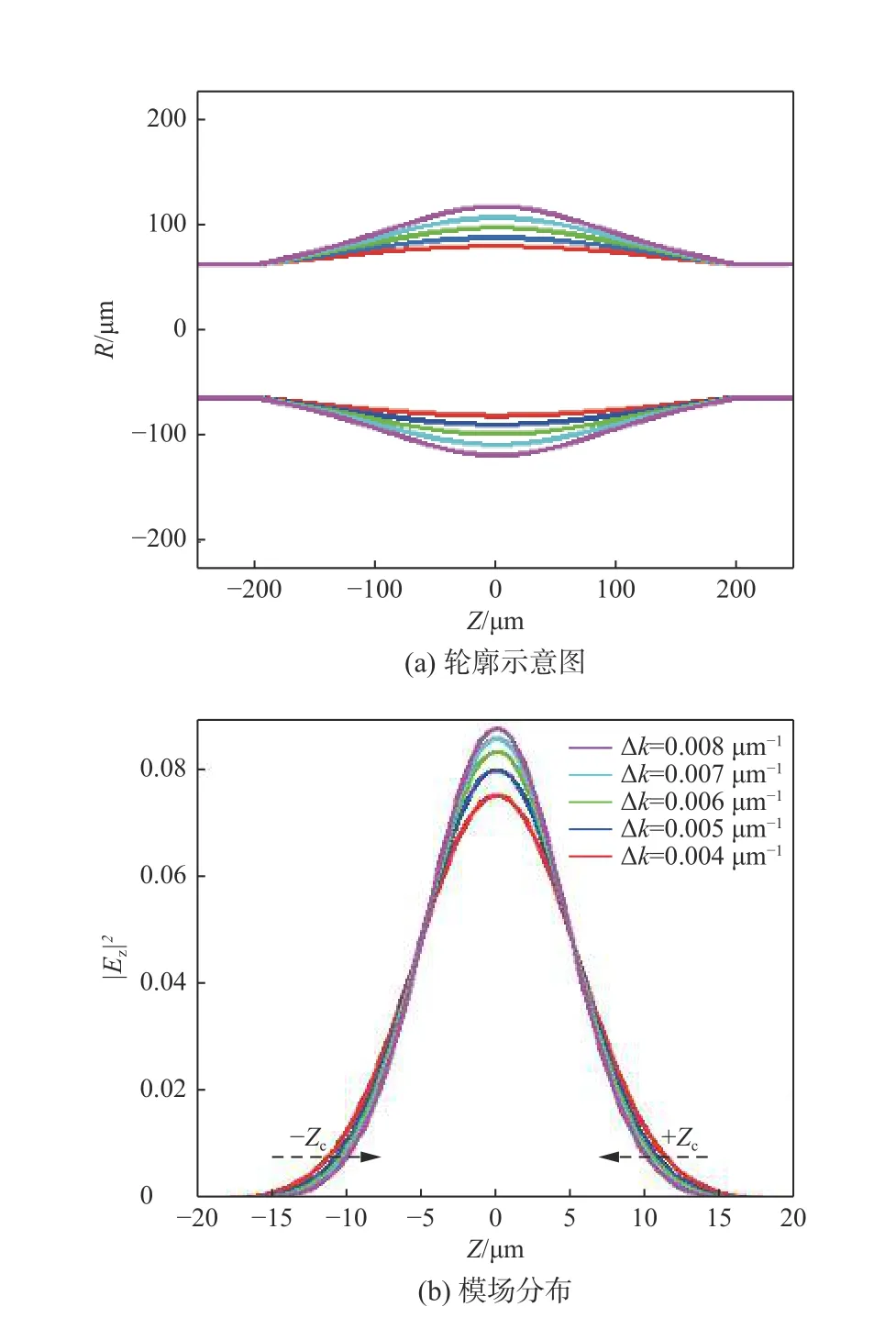
图2 不同曲率情况下空心微瓶谐振腔的轮廓示意图和模场分布Fig.2 Outline schematic and mode field distribution of hollowed micro-bottle resonator with different curvature Δk
此外,将参数中的Δk设置为恒定值0.003 μm−1,改变轴向量子数q分别为0、1、2和3,得到的光场分布情况如图3所示。随着q值的增加,激发出的轴向WGM 数量增加。模式的轴向阶次越高,光场越会朝着远离中心的位置拓展,但模式总是被限制在微瓶谐振腔的轴向方向上,呈现出两边幅值高于中间幅值的情况。

图3 轴向量子数q分别为0、1、2和3时所对应的轴向模式分布情况Fig.3 Axial mode distribution with axial quantum numberqof 0,1,2 and 3,respectively
2 器件制备
空心微瓶谐振腔是基于内径和外径分别为75 μm和126 μm的去涂覆石英毛细管(Innosep TSP075150)所制成的,制备过程如图4所示。首先,使用熔接机(FITEL S178)对石英毛细管的一端进行放电密封,放电强度为100 bit,放电时间为700 ms。然后,将另一端与注射泵相连,推动注射泵增加石英毛细管纤芯内的气压。最后在放电强度为1 bit和放电时间为300 ms的条件下,通过电极放电使熔融的石英毛细管内部气压受热膨胀形成瓶状结构。

图4 空心微瓶谐振腔的制备示意图Fig.4 Fabrication schematic of hollowed micro-bottle resonator
通过控制熔接机的放电次数,可以实现对空心微瓶谐振腔的尺寸控制。而随着鼓起程度的增大,石英毛细管的壁厚将会减小,采用表面积守恒法可以实现对壁厚的理论计算。图5中插图所示为空心微瓶谐振腔放电前后的横截面示意图。左边是未放电的石英毛细管,右边是放电之后的情况。图5中R1表示石英毛细管在放电前的外半径(63 μm),R2表示其相应的内半径,R3表示放电后的最大半径,d表示其相应的壁厚。此外,熔接机有上下两个相对的电极,可以保证石英毛细管在任一横截面上受到的温度是均匀且相等的,所以从横截面看去石英毛细管在放电前后的变化是均匀的,并且无论放电几次,理论上该圆环的表面积都应近似恒定。根据该理论可得:
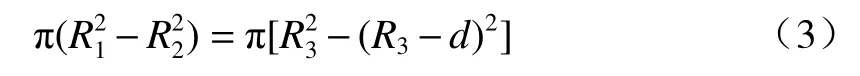
根据(3)式可以得到不同尺寸下空心微瓶谐振腔所对应的理论壁厚,如图5中曲线所示。随着空心微瓶谐振腔的尺寸增大,相对应的壁厚也就越小。
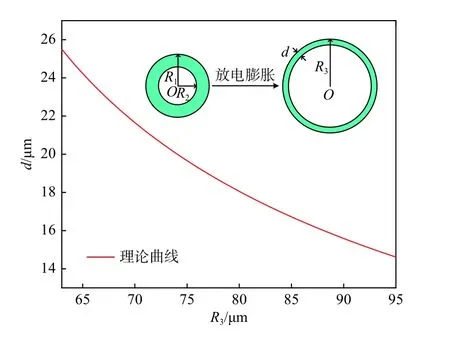
图5 最大半径R3与壁厚d之间的理论关系Fig.5 Theoretical relationship between maximum radius R3and wall thickness d
然后分析了不同放电次数下空心微瓶谐振腔的曲率变化。假设每次推动注射泵后造成石英毛细管纤芯内的气压变化为Px,温度变化为Tx。体积为Vx,即为石英毛细管的体积。设置熔接机的放电时间为300 ms,对其放电之后,温度上升到T1。通常,熔接机的放电时间比石英毛细管的膨胀时间长。因此,当温度仍为T1时,纤芯内的气压已经降低到标准大气压Po。根据理想气体状态方程,PV=ngasRgasT,其中P、V和T分别是理想气体的压强、体积和热力学温度,ngas是气体物质的量,Rgas是理想气体常数。在放电前,Vx=nRTx/Px。当放电次数为1时,V1=nRT1/Po,其中T1=Tx+k,k为电极放电所导致的温度变化。因此,可以得到以下公式:
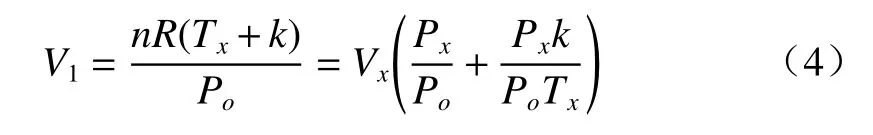
由于石英毛细管已经过1次放电,所以再次推动注射泵后,初始条件变为V1=nRTx/Px。当放电次数为2时,V2=nR(TX+k)/Po,可以推导出V2的表达式:
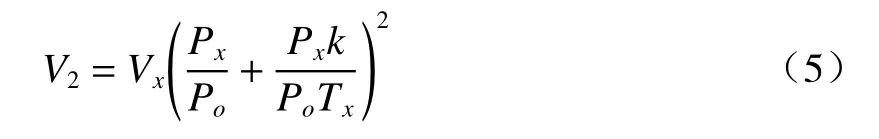
以此类推,当放电次数为N时,体积VN可以表示为
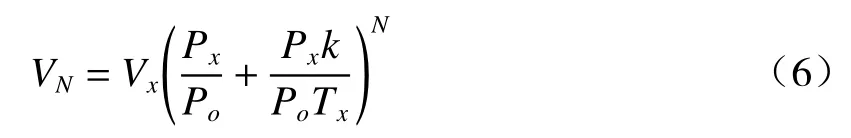
并且在制备过程中,石英毛细管的两端被夹具固定,在水平方向没有施加任何力。电极放电产生的高斯状电弧宽度也是固定的。因此,空心微瓶谐振腔的轴向长度可以近似看作是固定的。图6中插图所示是放电次数分别为2、3、4和5次时制备的空心微瓶谐振腔。经过测量轴向的长度约为400 μm,对应的最大半径R3分别为68.5 μm、74 μm、76.5 μm和91 μm。通过(1)式可以求得上述尺寸所对应的曲率∆k分别为0.002 2 μm−1、0.003 2 μm−1、0.003 5 μm−1和0.005 3 μm−1。通过热膨胀形成的空心微瓶谐振腔可以视为圆柱体和椭球体的组合:

式中:ΔR=R3−R1;L表示空心微瓶谐振腔沿Z轴的一半长度。所以我们可以得到下式:
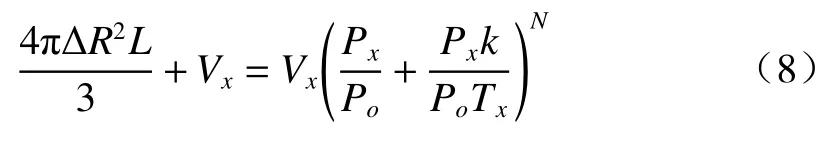
由于R3=ΔR+R1,结合(8)式可得R3与N的关系:

根据描述微瓶谐振腔轮廓的(1)式,可以求得曲率∆k与放电次数N之间的关系:
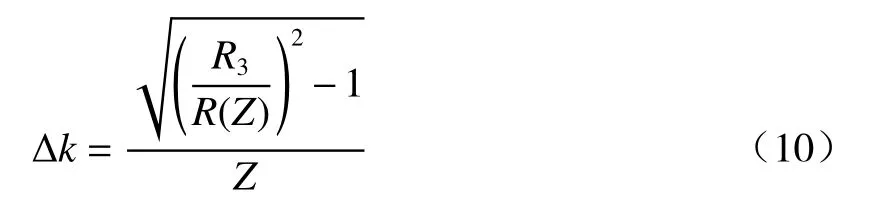
根据(10)式可以计算出图6中反映∆k与N之间关系的曲线,插图为放电次数分别是2、3、4和5时器件的显微镜图像。参数Z=200 μm,R(Z)=63 μm。参数S=Px/Po+(Pxk)/(PoTx),取值为2.5。结果表明,随着放电次数的增加,∆k的增长速率变大。实验结果符合理论曲线的变化趋势。
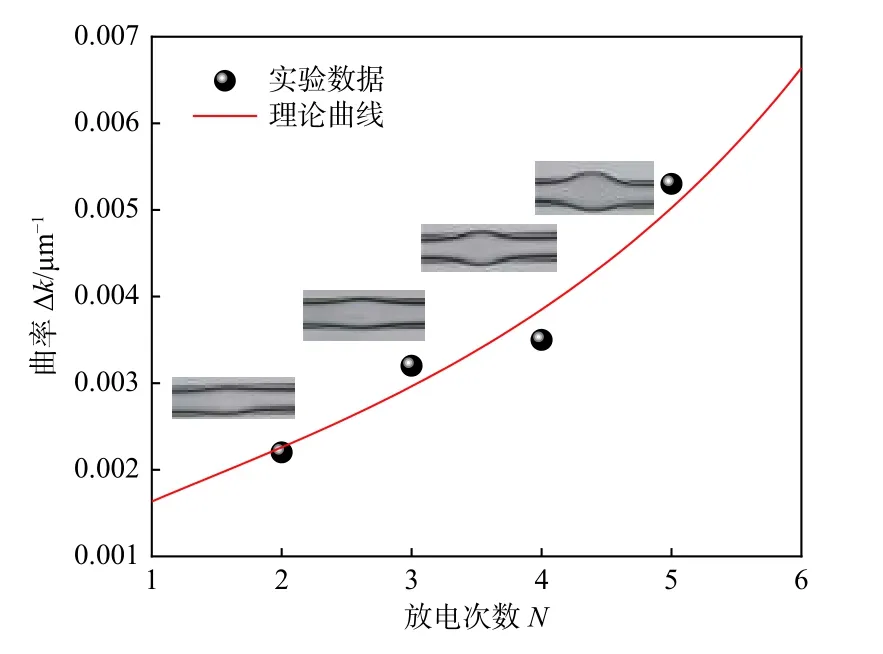
图6 放电次数N和曲率∆k之间的关系Fig.6 Relationship between discharge times Nand curvature ∆k
3 传输特性分析
通过锥腰直径为2 μm的微纳光纤融锥与空心微瓶谐振腔耦合来激发WGM,实验装置如图7所示。图7中红色线路表示光路,黑色线路表示电路。空心微瓶谐振腔与微纳光纤融锥之间的耦合距离由2个分辨率为20 nm的三维调整架(Thorlabs NanoMax300)来精确控制。利用CCD(chargecoupled device,电荷耦合器件)观察两者之间的位置,图7中的图像即为在CCD 下观察到的耦合情况。并且为了提高耦合实验的稳定性,将微纳光纤融锥贴在空心微瓶谐振腔的表面。然后,可调谐激光器(Agilent 8164)发出的光经过偏振控制器(Newport F-POL-APC)后耦合到空心微瓶谐振腔中,其中光功率为100 μW,偏振控制器用来调节光的偏振态。光信号经过光电探测器(Thorlabs DET08CFC/M)转化为电信号后被示波器(Tektronix MSO4104)记录。
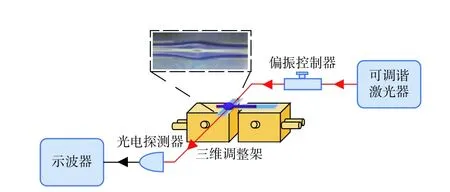
图7 实验装置示意图Fig.7 Schematic of experimental device
搭建好上述装置后,选取曲率∆k分别为0.002 2 μm−1、0.003 2 μm−1、0.003 5 μm−1和0.005 3 μm−1的空心微瓶谐振腔进行测试。测试结果如图8所示。从图8中可以观察到在1 545 nm~1 550 nm范围内,丰富且密集的WGM 被有效激发。这是由于瓶状结构的非球面特性使得空心微瓶谐振腔支持2种方向上的模式,一种是在赤道面环绕的径向WGM,另一种是在轴向上螺旋传播的轴向WGM。并且谐振波长和激发强度还取决于微纳光纤融锥与谐振腔模场之间的相位匹配程度和空间重叠度[15]。当微纳光纤融锥放置在空心微瓶谐振腔的中心附近时,所有的轴向WGM是最容易被激发的。
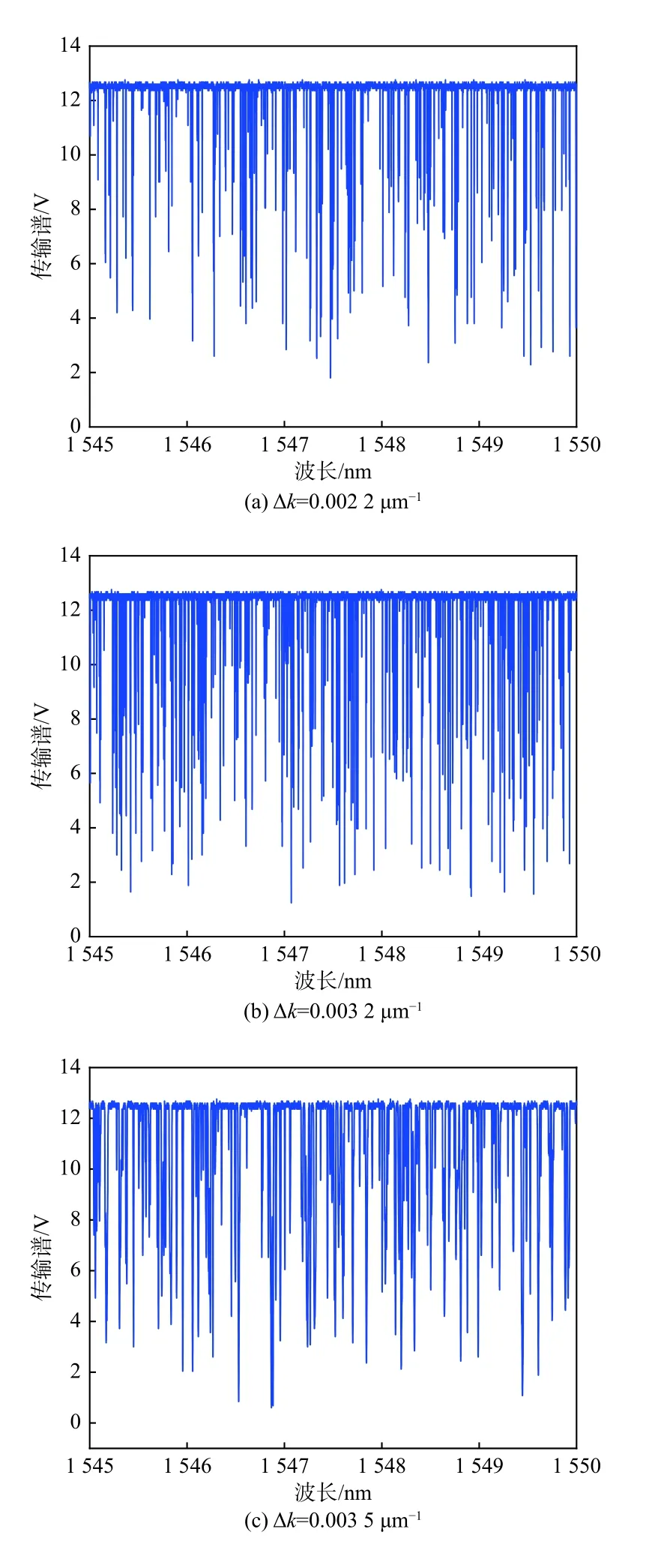

图8 不同曲率∆k对应的实验结果Fig.8 Experimental results corresponding to different curvature ∆k
然后在图9中放大了不同曲率下传输谱的测试结果。所选取的谐振波长分别为1 547.346 nm、1 547.270 nm、1 547.347 nm和1 547.253 nm。经过拟合后,根据Q-factor 公式(定义为Q=λ/∆λ),其中波长λ为谐振波长,∆λ为半高全宽,求得Q-factor分别为5.12×105、5.95×105、6.34×105和7.26×105。随着空心微瓶谐振腔曲率∆k的增大,谐振腔的Q-factor也随之增加。但是微纳光纤融锥是直接贴在空心微瓶谐振腔的表面,使得大多数WGM处于过耦合状态会导致较低的Q-factor[21]。在后续研究中,我们可以通过改进实验装置实现临界耦合状态或者优化制备工艺制得表面更光滑的器件来进一步提升Q-factor。
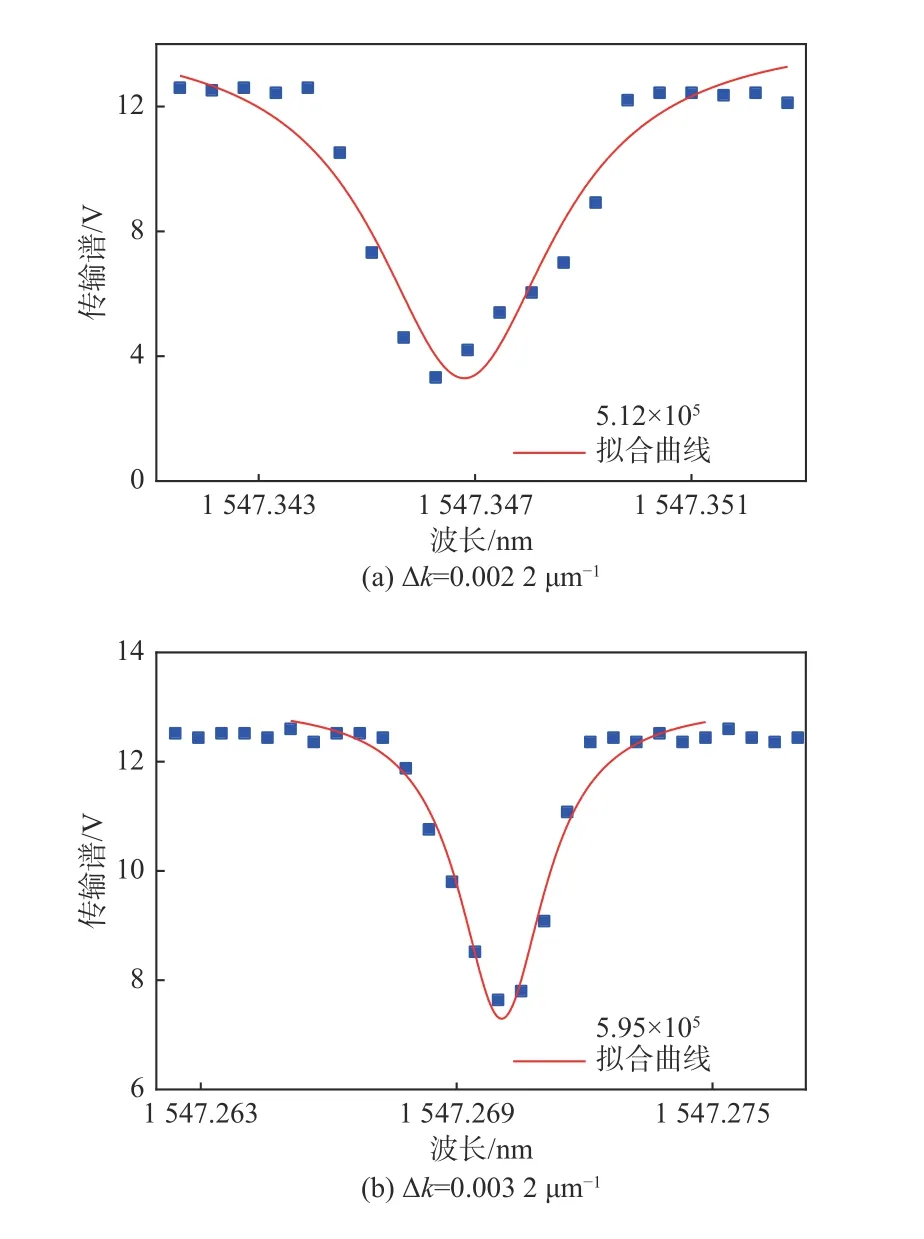
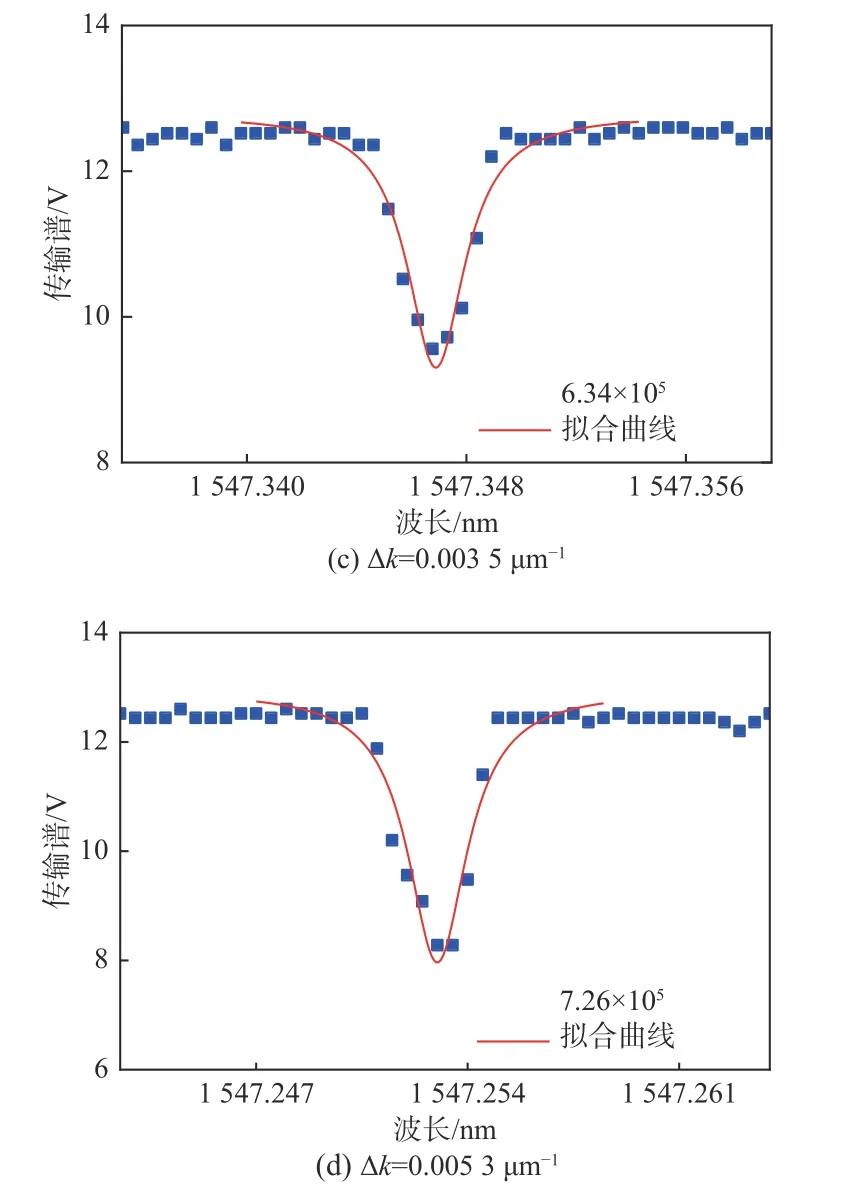
图9 不同曲率∆k的单个谐振峰结果Fig.9 Single resonance peak results with different curvature ∆k
最后在图10中展示了Q-factor 随着曲率∆k的变化趋势。当∆k从0.002 2 μm−1增加到0.005 3 μm−1时,Q-factor 从5.12×105增加到了7.26×105。结果表明随着∆k的增大,空心微瓶谐振腔的Q-factor越高,相应的谐振腔内所储存的光场能量也就越大,与仿真结果一致。
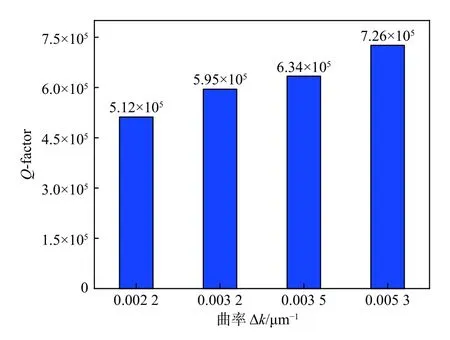
图10 空心微瓶谐振腔的Q-factor和曲率∆k之间的关系Fig.10 Relationship between Q-factor and curvature ∆kof hollowed micro-bottle resonator
4 结论
本文提出了空心微瓶谐振腔的曲率变化模型并且研究了曲率对其传输特性的影响。从理论角度仿真了微瓶谐振腔内轴向WGM的分布情况。随着微瓶谐振腔的曲率增大,内部基模的能量幅值也会相应增加。利用熔接机放电沿石英毛细管制得不同曲率的瓶状结构。根据理想气体状态方程,分析了放电次数对空心微瓶谐振腔曲率的影响,理论趋势与实验结果相符合。通过实验测试了不同曲率空心微瓶谐振腔的传输谱。随着∆k增大,空心微瓶谐振腔对光的束缚能力越强,得到的Q-factor 也就越高,达到了7.26×105。在接下来的研究中可以将微瓶谐振腔的空心作为液体通道,将具有折射率可调特性的磁流体填充进去,利用其轴向WGM 增强光与内部磁流体的相互作用,通过监测谐振波长的变化实现磁场传感。

