反向追迹法获取水下对空全景图像
(华中光电技术研究所 武汉光电国家研究中心,湖北 武汉 430223)
引言
从水下透过波浪观察海面及空中目标的方法由美国Areté公司提出[1],为水下对空探测提供了一种有效的途径,被称为虚拟潜望镜技术。该技术可用于水下平台对海空目标的隐蔽探测,在军事上有重要应用,潜艇借此可以在不浮出海面的情况下实现对海面船只及空中反潜机的探测,实现潜艇上浮避碰及在水下安全深度对空警戒,极大地增加了潜艇的安全性。
水下对空成像属跨介质成像,光线经过水-空气界面时会发生折射,且海面常处于动态变化过程中,给水下对空成像带来畸变和像差等不利影响。当光线从空气中折射入水后,会产生色散效应,海水吸收和散射会使能量衰减并带来图像模糊,在这些因素的综合作用下,获取高质量的水下对空图像十分困难,因此,虚拟潜望镜技术至今离实际应用还有一定距离。然而,国内外学者根据水下对空成像的特点,重点从某一方面进行研究,仍然取得了重要进展。例如,文献[2]分析了接近水天线目标的色散情况,并给出了利用楔形镜校正色差的具体方法;文献[3]提出了一种水下对空成像的光学计算模型,利用光线追迹分析波浪对光线的扰动,得到了水下像面照度的分布;文献[4]中赵文强等研究了水下对空成像Snell 窗口的光学问题,解决了水下对空等效入瞳、波面曲率的等效光学特性以及天空亮度分布的计算问题;文献[5]通过计算Snell圆域的扩展程度对海面波浪大小进行估算;文献[6]以一维海浪为例,通过定量计算太阳像的变化来估算海面海情,文献[7]研究了从空中观察水底目标时产生的畸变,并给出了一种图像畸变校正算法,文献[8]则分析了波浪斜率对太阳反射光斑的影响,这些工作主要从定量计算的角度分析波浪对水下对空成像的影响,是本文研究的基础。文献[9-11]分析了动态波面对水下图像重建的影响,提出了水下光学系统的设计思路,美国专利[12]提出了透过波动海面成像的方法及系统设计,文献[13-14]主要基于统计原理,阐述了利用中心法对水下对空畸变图像进行复原处理,文献[15-16]则重点分析了畸变向量场的几何变换方法,运用波动视频中相邻两幅图像之间的相关关系对图像进行复原,取得了较好的效果,这些工作也为本文研究提供了有益的借鉴。
本文以海面波形对水下对空图像的畸变影响为重点,通过MATLAB 仿真,利用主光线反向追迹获取水下对空全景图像,在假定海浪具有4种典型的三维表达式(海面平静、径向波浪、柱面波浪、二维正弦波浪)的情况下给出了仿真图像的计算结果,为分析水下对空图像的畸变特性提供了一种有效手段,该仿真方法可适用于具有连续一阶偏导波形的波浪,为研究更复杂波浪下的水下对空图像畸变特性奠定了基础。
1 水下对空全景成像计算模型
1.1 水下对空全景成像系统组成
为简化水下对空成像的计算过程,可建立如下理想化的成像模型。如图1为水下对空成像系统示意图,系统主要包括水下成像镜头和成像靶面,工作时假定光轴竖直向上。目标光线从空中入射到海面上,经水-气界面折射后在水中向下传输,直到被水下镜头收集并折射到靶面上形成像点。从成像过程来看,应将海面及系统上方海水看作水下光学系统的一部分,且波动的海面是一块动态变化的透镜,会使图像产生动态的畸变。
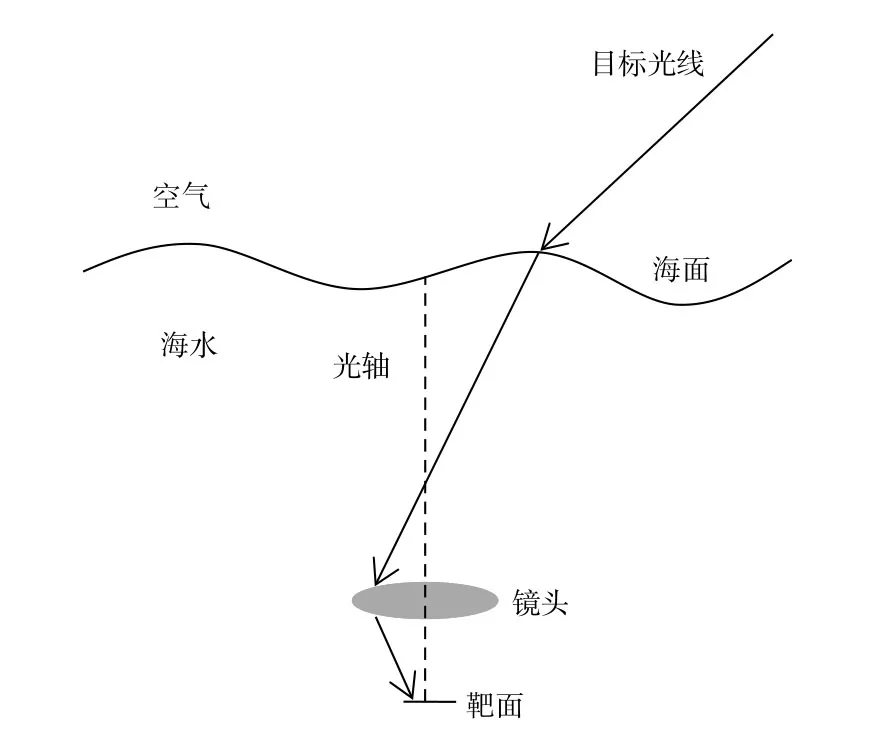
图1 水下对空成像系统示意图Fig.1 Schematic of water-to-air imaging system
由于光线在水下会发生全反射现象,因此在海面平静时,要实现对半球全空域的观察,水下对空成像系统的视场至少为97.2°[4]。当海面有波浪时,为了观察到全空域,则需要适当扩大观察视场,在本文中,设定水下对空成像视场横纵两个方向的大小均为120°。
1.2 基于反向追迹法的水下对空成像计算模型
为使水下对空成像的计算简洁,假定目标处于无穷远处的天球之上,而水下对空成像系统所在区域的海平面为天球赤道,海面平静时光轴与海平面的交点为天球中心,下面分条详细描述该计算模型。
1) 建立坐标系
天球坐标系:以水下对空成像系统光轴与海平面交点O为天球中心,当地海平面为天球赤道,竖直向上方向为天球北极方向。不失一般性,设正东方为赤经0°方向(若当地为南北两极,则取0°经线方向为赤经0°方向),逆时针为赤经正向。设天球赤道的赤纬为0°,往天球北极方向为赤纬正向。
水下对空成像系统坐标系:靶面水平放置,光轴竖直向上为z轴正向,正东方为x轴正向,正北方为y轴正向,成像系统的光心为坐标原点,由此建立了天球与成像系统之间的坐标联系。
2) 主光线反向追迹
假定水下对空成像系统满足小孔成像模型,且对成像靶面上的每个像素点只考虑其主光线的折射路径,设入射光线由水下对空成像系统发出,其方向矢量由成像系统光心C指向某一像素点p,如图2。入射光线经海面折射后射入空中,折射光线矢量具有赤经和赤纬两个参量,这对应于天球上的一点,这一点与像素点p正好满足物像对应关系。

图2 靶面像素点的主光线反向追迹示意图Fig.2 Schematic of main-ray inverse tracing of target surface pixel points
设成像靶面为正方形,水平放置,E点为靶面中心,像素点p的二维坐标为(cx,cy),C点为成像系统光心,CE为焦距f,Cp则为像素点p的主光线的反向追迹,本文把它作为入射光线,Cp的方向矢量为

已知C点空间坐标及Cp的空间方向矢量,易得Cp的空间直线方程,设海面瞬时波面方程为

求出入射光线Cp与海面的交点(x0,y0),得到点(x0,y0)处海面的法线方向矢量

根据Snell定律

在三维空间中计算出折射光线的方向矢量,得到p点在天球的对应点P。其中i为入射角;r为折射角;n为海水折射率。
3) 建立物像对应关系
由上可知天球上P点与靶面像素点p为物像共轭关系,作过E、C、p3点的竖直截面进行说明。如图3,入射光线Cp延长与海面交于F点,出水后得到折射光线FQ,过O点作FQ的平行线,延长后与天球交于P,则P与矢量FQ对应,即天球上点P与像素点p具有物像共轭关系。
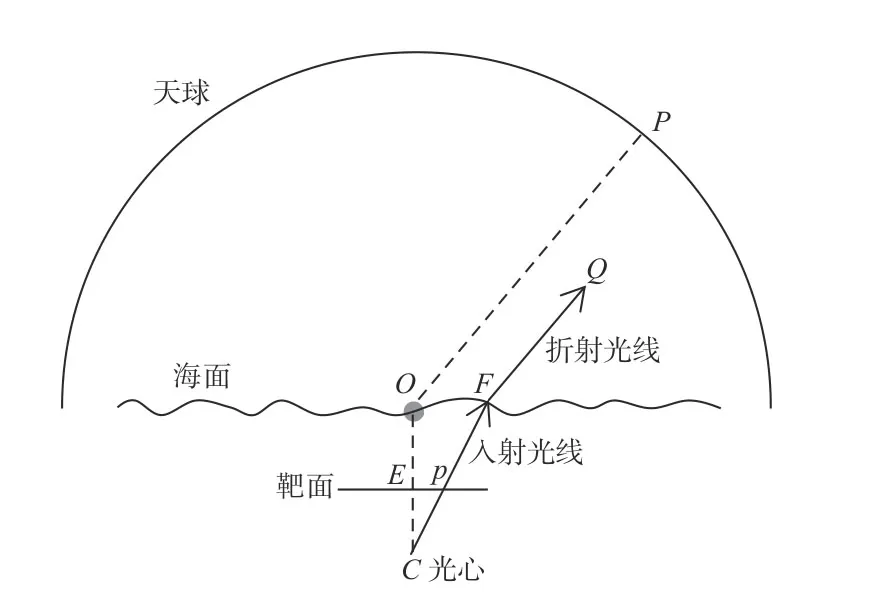
图3 靶面像素点与天球目标点的对应Fig.3 Correspondence of pixel point on target surface and target point on celestial sphere
4) 遍历全部像素点得到对空全景图像
若对成像靶面上全部像素点进行遍历,则得到一幅完整的水下对空图像。若成像视场足够大,则该图像为水下对空全景图像。
2 典型波面及场景下的水下对空全景图像仿真
2.1 水下对空全景图像计算流程
根据以上建立的水下对空成像模型,可以利用反向追迹法逐点重构出整幅图像,具体如下:
1) 设定天球目标场景;
2) 给出海面的波面方程;
3) 设定成像系统探测视场、分辨率、焦距、工作深度等成像参数;
4) 对成像靶面所有像素点进行遍历,每个像素点需完成5)~9)之间的操作;
5) 求出像素点对应的入射光线的直线方程;
6) 求出入射光线与波面的交点(x0,y0);
7) 求出过点(x0,y0)的波面法线方程;
8) 根据Snell定律求出折射光线方向矢量;
9) 求出与折射光线对应的天球目标点,该点的灰度值即为对应像素点的灰度值;
10) 输出水下对空全景图像。
入射光线与波面的交点可用二分法进行求解,如图4所示,具体过程:设入射光线的两个端点C和D处于波面异侧,其坐标分别为和则与异号,不妨设V1>0,V2<0。设并设F点的坐标为计算若V0>0,则将C点坐标更新为若V0<0,则将D点坐标更新为继续对端点C和D进行以上迭代计算,直至V0的绝对值小于给定的小正数为止,此时即为直线与波面的交点近似解。

图4 二分法求解直线与曲面交点Fig.4 Solving intersection of straight line and curved surface by bisection method
根据Snell定律计算折射光线矢量需要在三维空间中求解,如图5所示,过程如下:设入射光线、折射光线及法线的方向矢量分别为R=(rx,ry,rz)和N=(nx,ny,nz),由于事先已求得F点的坐标故I和N均为已知量,设入射角为i,折射角为r,则有i=arccos(I·N),r=arccos(R·N),由于R为单位矢量,故|R|=1,由Snell定律,有n·sin(i)=sin(r),由于I、R和N3个矢量必须共面,故I×N·R=0,由于入射光线与折射光线必须位于在法线的两侧,故(I×N)·(R×N)≥0。根据以上条件,可以联立解出折射光线的方向矢量R,即(rx,ry,rz)。
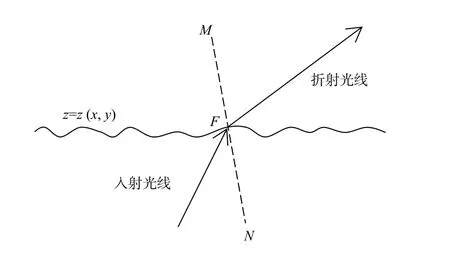
图5 三维空间中求解折射光线矢量Fig.5 Solving direction vector of refracted ray in 3D space
2.2 边界条件设定
对天球目标场景、成像参数及波面方程进行如下设定。
1) 天球目标场景
设定4个天球目标及背景如表1,即灰度值为255、角直径为10°的4个圆形亮目标悬挂在灰度值为128的均匀亮度天空中,位于正东方,高度角分别为10°、30°、60°、90°。

表1 天球目标场景Table1 Celestial sphere target scenes
2) 成像系统参数
海面平静时Snell圆锥的张角为97.2°,海面有波浪时水下视场会增大,故设定成像系统的探测视场大小为120°×120°,靶面分辨率为1024×1024像素,镜头焦距为3 mm,工作水深为50 m。在以下仿真计算中,假定成像系统没有像差和畸变,满足小孔成像原理。
3) 波面方程
设定波面方程为4种形式:海面平静;径向波浪;柱面波浪;二维正弦波浪。具体在下文详细描述。
2.3 水下对空全景图像计算结果
2.3.1 海面平静下的计算结果
海面平静时的波面方程为

此时半球天空在靶面上的像正好是一个圆,且其对应的水下视场为97.2°,由于水下对空全景成像系统的视场为120°,因此在此Snell圆区域之外由于发生全反射现象而为纯黑色。如图6,灰色大圆为Snell圆,即半球天空所成像的区域,天球上的4个圆形目标在靶面上所成的像从右往左依次对应1、2、3和4 号目标,即图中的白色区域,赤纬角小的1 号目标像靠近Snell圆边缘,而正当空的4 号目标像在Snell圆中心。

图6 海面平静时水下对空全景图像Fig.6 Water-to-air panoramic image under calm sea surface
2.3.2 径向波浪下的计算结果
海面为径向波浪时,其波面方程为
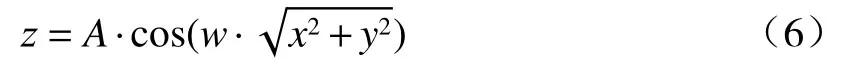
图7是该波面方程的直观外形示意图。

图7 径向波浪波形示意图Fig.7 Schematic of radial waveform
由图可见径向波浪是以一点为中心的旋转对称的同心圆,它由平面余弦曲线绕z轴旋转一周生成,如(7)式所示:

水下对空全景成像系统处于径向波浪中心正下方一定深度处,通过以下MATLAB 代码来确定径向波浪的波形参数:

其中:A为波浪振幅;w为波浪角频率;T为波长;steep为波陡,即波高与波长的比值;depth表示成像系统光心C的深度;DIA为观察视场在海面的宽度;N表示视场宽度范围内波浪的周期数;波高为振幅A的两倍。在以上成像参数条件下,通过MATLAB 仿真得到图8所示全景图像。

图8 径向波浪下水下对空全景图像Fig.8 Water-to-air panoramic image under radial wave
如图8,由于波浪的旋转对称特征,天球区域的图像仍然是灰色大圆,直观看来图8与图6相似,其中目标1到目标4的白色像次序也一致,但仔细对照可以发现图8的Snell圆直径比图6大,4个目标像的形态也不相同,其位置也存在一定的偏移,特别地,两图中目标4的图像直径不同。
2.3.3 柱面波浪下的计算结果
海面为柱面波浪时,其波面方程为

图9是该波面方程的直观外形示意图。

图9 柱面波浪波形示意图Fig.9 Schematic of cylindrical waveform
波形参数取值与2.3.2节一致,通过MATLAB仿真得到图10所示水下对空全景图像,可以明显看出Snell圆的边缘已经发生明显的变形,4个天球目标像的位置次序虽一致,但其形态和位置都与图6有一定变化,特别地,最左边目标4的白色像不再是圆。

图10 柱面波浪下水下对空全景图像Fig.10 Water-to-air panoramic image under cylindrical wave
2.3.4 二维正弦波浪下的计算结果
海面为二维正弦波浪时,其波面方程为

图11是该波面方程的直观外形示意图。

图11 二维正弦波浪波形示意图Fig.11 Schematic of 2D sinusoidal waveform
波形参数取值与2.3.2节一致,且取
由此通过MATLAB 仿真得到图12所示水下对空全景图像。可以看到,Snell圆的边缘发生了更复杂的变形,4个天球目标的位置次序虽一致,但其形态和位置都与图6有一定变化,其中目标1的图像的形变特别大,目标4的图像也不是圆。

图12 二维正弦波浪下水下对空全景图像Fig.12 Water-to-air panoramic image under 2D sinusoidal wave
2.4 波面参数对水下对空全景图像的影响
上文分别给出了海面平静、径向波浪、柱面波浪及二维正弦波浪下的水下对空全景仿真图像,仿真中波陡steep取了较小值,视场内波浪的周期数N也较小,这种情况下4个天球目标的像畸变不是特别严重。事实上,在较大波浪下,每个圆形目标的图像极易分裂成多个,为避免碎化后的目标像混叠难以分辨,下文仅对天球目标2 进行仿真。由于当波陡steep和视场内波浪周期数N这两个参数确定后,水下对空全景图像也就确定,与成像系统的深度depth无关,因此,下面只考察steep和N的变化对全景图像的影响。
2.4.1 径向波浪波面参数变化的影响
严格来说,应对steep和N分别取一系列值来仿真水下对空图像,为了直观和简洁起见,下面各节均在两种情况下给出仿真结果:一是steep取固定值,N取4个不同值;二是N取固定值,steep取4个不同值。具体取值以能直观展示图像的变化趋势来确定。
图13为steep=0.05时目标2的仿真图像。由图可见,随着N值增大,天球成像区域大小变化较小,但目标2的图像逐渐碎化。

图13 steep=0.05时目标2的仿真图像Fig.13 Simulated images of target No.2 when steepis 0.05
图14为N=10时目标2的仿真图像。由图可见,随着steep值增大,目标2的图像逐渐碎化,同时Snell圆域也向外扩展。

图14 N=10时目标2的仿真图像Fig.14 Simulated images of target No.2 when Nis 10
2.4.2 柱面波浪波面参数变化的影响
图15为steep=0.05时目标2的仿真图像。由图可见,随着N值增大,天球成像区域大小变化较小,但目标2的图像逐渐碎化。
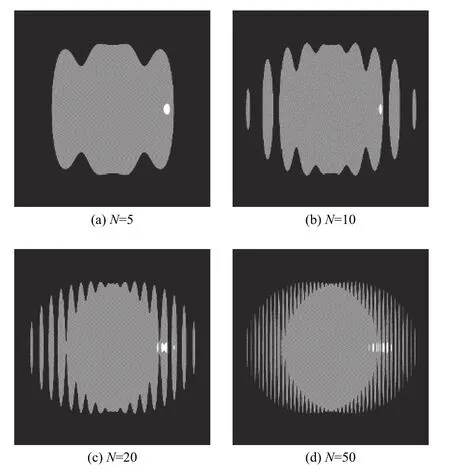
图15 steep=0.05时目标2的仿真图像Fig.15 Simulated images of target No.2 when steep=0.05
图16为N=10时目标2的仿真图像。由图可见,随着steep值增大,目标2的图像逐渐碎化,同时Snell圆域也向外扩展。
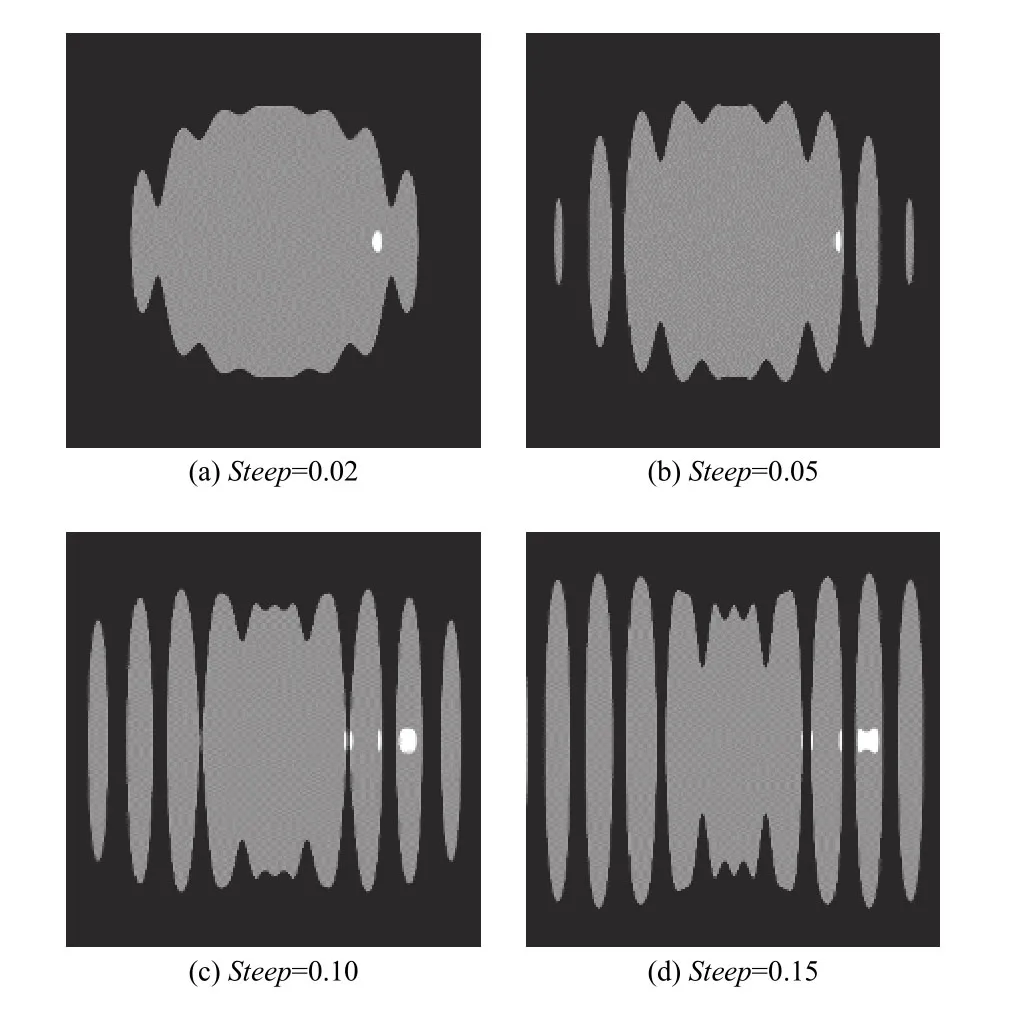
图16 N=10时目标2的仿真图像Fig.16 Simulated images of target No.2 when N=10
2.4.3 二维正弦波浪波面参数变化的影响
图17为steep=0.05时目标2的仿真图像。由图可见,随着N值增大,天球成像区域大小变化较小,但目标2的图像逐渐碎化。

图17 steep=0.05时目标2的仿真图像Fig.17 Simulated images of target No.2 when steep=0.05
图18为N=10时目标2的仿真图像。由图可见,随着steep值增大,目标2的图像逐渐碎化,同时Snell圆域也向外扩展。

图18 N=10时目标2的仿真图像Fig.18 Simulated images of target No.2 when N=10
2.4.4 波浪参数对水下对空成像的定量影响
由以上3小节给出的仿真结果可以看出,波浪周期数N显著影响图像的碎化程度,但对整个成像区域的扩展程度影响很小,而波陡steep既能影响图像的碎化程度,同时又显著影响图像的扩展程度,这是波浪参数对水下对空成像的定性影响。然而,根据本文提出的计算方法,只要给定波浪参数,仿真程序实际上已经输出了对空图像定量结果,可以从仿真结果确切计算出成像区域的扩展程度与波浪参数的对应关系,而且当给出波浪的运动方程时,也完全可以仿真出对空图像随波浪变化的视频。
3 结论
本文利用主光线反向追迹法仿真水下对空全景图像,给出了根据Snell定律求解水下对空全景图像的一般过程。在海面平静、径向波浪、柱面波浪和二维正弦波浪下得到了典型天球目标及背景的图像,同时,通过改变波陡和视场内波浪周期数两个波浪参数,直观地表现了波浪的变化对水下对空全景图像的影响。根据建立的成像模型,在水下对空全景图像、波浪方程和天球目标场景三者之间,若已知其中两个,则可求出另一个,这为分析水下对空成像的畸变特性提供了定量的方法。该方法适用于分析透过具有一阶可导波浪的水下对空全景图像的畸变特征,为研究更复杂波浪下的水下对空图像畸变特征奠定了基础。
然而,波浪对水下对空成像的影响十分复杂,除了利用主光线反向追迹所描述的图像畸变之外,在实际成像过程中还存在离焦、色散、偏振、散射、吸收、成像噪声等多方面的不利影响,太阳不可避免地进入视场后也会对成像产生干扰,这些因素将严重降低水下对空成像质量,增加目标探测和识别的难度。因此,还需对这些问题进行深入研究。

