基于非均匀采样的ϕ-OTDR仿真与信号处理∗

（海军工程大学电子工程学院 武汉 430000）

1 引言

相位敏感光时域反射计（ϕ-OTDR）是一种分布式的光纤传感技术。由于其抗电磁干扰、灵敏度高、定位精确、数据处理相对简单等特点，在大型建筑的健康监测，海底管线的安全监控，国家边界安全等领域得到了广泛的应用［1］。但是传统的ϕ-OTDR系统由于受到光波在光纤内往返时间的制约，根据奈奎斯特采样定理，其最高响应频率只能达到探测脉冲频率的一半。特别是对于一些长距离的ϕ-OTDR传感系统，探测频率的响应范围会出现十分显著的下降。文献［2］中的ϕ-OTDR系统传感距离达到了175km，但是相应的最高响应频率只有285Hz。针对这一问题，2017年Zhang提出可以利用非均匀采样方法，通过随机调制探测脉冲的时间间隔，突破奈奎斯特采样定理的限制，提高ϕ-OTDR系统的最高响应频率。在最高采样频率为10kHz的系统中，可以探测到1.153MHz的单频振动［3］。在文献［4］中，Zhang进一步对这一方法中各参数的最优取值进行了分析。但是，他仅仅分析了非均匀采样法如何探测振动频率，对这一方法如何用于定位并没有研究。而传统的ϕ-OTDR系统信号处理技术，如移动平均并对平均结果做差分的方法（以下简称移动平均法），主要是应用于均匀采样信号的定位［5］，对非均匀采样信号效果并不理想。本文首先分析了ϕ-OTDR系统探测原理，并借鉴光栅设计中的离散层剥离思想，对ϕ-OTDR系统探测过程中产生的瑞利散射光信号进行了仿真模拟。其次，针对基于非均匀采样方法的ϕ-OT⁃DR系统特性，提出了一种利用频域信号标准差的改变值来定位振源位置的方法，并对这一方法的抗噪性能，以及振动信号的频域稀疏度等进行了分析。

2 ϕ-OTDR系统探测原理

2.1 系统构成

ϕ-OTDR的系统框图如图1所示，光源发出稳定的超窄线宽激光，经由声光调制器（AOM）调制为周期性的光脉冲，在通过掺铒光纤放大器（ED⁃FA）并滤除噪声后经环形器注入到光纤链路。光脉冲在传播过程中，会在光纤沿线不断产生后向瑞利散射光，并且由于瑞利散射是弹性散射，产生的散射光会发生多光束干涉，返回的干涉光进入光电探测器（APD）变为电信号，然后经数字采集器（DAQ）转换为数字信号，这样终端处就得到了一条沿时间轴分布的瑞利散射曲线，并且时间点与光纤距离对应。当光纤上某点发生振动时，相应位置处瑞利散射光相位会发生改变，进而造成接收端瑞利散射曲线的变化，通过探测这一变化，就可以定位振动源并求得振动频率。

图1 ϕ-OTDR系统框图

2.2 探测原理

ϕ-OTDR主要是通过探测光纤中返回到入射端的瑞利散射光的干涉图样，从而实现分布式光纤传感。所谓瑞利散射光，就是指远小于光波长的粒子所引起的光弹性散射（散射光与入射光频率相同）。具体到光纤中，则是指光纤中远小于入射光波长的不均匀性所引起的光弹性散射。这种不均匀性是在光纤拉制过程中固化在光纤中的，可以等效看作是光纤内折射率的不均匀起伏［6］。

由于ϕ-OTDR使用的是频率稳定的超窄线宽光源，而且探测脉冲具有一定的宽度，所以在脉冲内部不同位置处会产生众多的瑞利散射光，而且不同时刻产生的散射光在返回时会叠加在一块，所以接收端接收到的散射光信号实际是多束瑞利散射光干涉的结果，如图2所示。

图2 光纤内相干瑞利散射光的生成原理图

在图2（a）中，矩形光脉冲在t0时刻前端运动到了a0点，此时aN点是光脉冲的中点。这个脉冲所覆盖的光纤可以划分为2N个极窄的光纤微元（宽度为ΔL），设第i个微元产生的后向瑞利散射光可表示为（图2中用黑色箭头表示），则t0时刻一共产生了2N个。设tN时刻光脉冲的末端运动到aN点（图2（b）），此时，第2N个微元中除了tN时刻产生的，还包含之前时刻产生的，所以综上所述，在tN时刻第N个光纤微元中总的后向瑞利散射光Er可以表示为

随着光脉冲的前进，光纤上的每个ΔL内都会产生一个Er，而ϕ-OTDR正是通过探测并记录各时刻返回的Er，从而实现分布式的光纤传感。

3 ϕ-OTDR仿真

3.1 仿真模型设计

1998年Park等将ϕ-OTDR的基本理论模型抽象为将光纤分成N段，在每小段光纤中存在若干个反射率和相位变化随机取值的反射镜，用反射镜的反射光来等效后向瑞利散射光。这一模型很好地解释了ϕ-OTDR的物理规律，且符合实验结果［7］。但是这一模型没有将振动造成的折射率波动与散射光的相位变化情况很好地联系起来，不利于计算机仿真的实现。因此，本文提出将每小段光纤中的反射镜替换成一段布拉格光栅，利用光栅设计的相关公式，在光纤折射率与瑞利散射光相位之间建立联系。

已知均匀布拉格光栅的反射光波长λr=2n0Λ，其中n0是光纤群折射率，Λ是栅距。所以只要控制Λ就可以得到和入射光波长相同的反射光。假设反射光的频谱是超窄线宽的，并且满足光栅相位匹配条件，基于模式耦合理论，可以得到光栅的反射率R和反射光的相位改变值φr［8］：

其中，lF是光栅长度，C是耦合系数，且C与光纤折射率的波动幅度Δn有如下关系：

这样一来，我们只要知道了光纤上每一点的折射率起伏值Δn，就可以算出相应位置处后向瑞利散射光的反射率R和相位改变值φr。由式（1）可知，后向瑞利散射光的相干只发生在长度为NΔL的光纤段内，所以借鉴离散层剥离算法的思想［9］，我们可以把对瑞利散射光的求解控制在NΔL层光纤内。随着光脉冲的前进，不断迭代求得整条光纤上的后向瑞利散射光分布。

3.2 数值仿真

在光波长为1550nm时，单模光纤中的瑞利散射损耗系数约为0.16×10-3dB/m，其中后向瑞利散射光占比约为Br≈ 0.082%［10］，所以 R 的均值。已知，只要合理设置lF的值，通过式（2）、（4）即可求得光纤上折射率的波动幅度均值。假设光纤中的不均匀性符合瑞利分布，可以利用Matlab生成期望是，满足瑞利分布的Δn（z）数组，为每个光纤微元赋值，再代入式（4）求出C（z），进而求得每个光纤微元内的R与φr。已知光纤各位置处的R与φr，则只要预设好入射光脉冲的初始参数，利用式（1），就可以得到整条光纤上后向瑞利散射光的干涉曲线。

设仿真数值如表1所示。

利用表1参数，仿真得到ϕ-OTDR在一个脉冲周期内产生的瑞利散射光信号。如图3，这是长度为3km和30km光纤上的后向瑞利散射光功率分布曲线。从图3（b）中可以看到，随着光纤距离的增长，瑞利散射光强度迅速衰减。因为单模光纤中的后向瑞利散射光信号极其微弱，远端光纤链路上的后向散射光信号通常会淹没在噪声中。因此必须使用有效的信号处理手段，从噪声中提取信号，以实现对光纤链路的分布式监测。

表1 仿真数值与说明

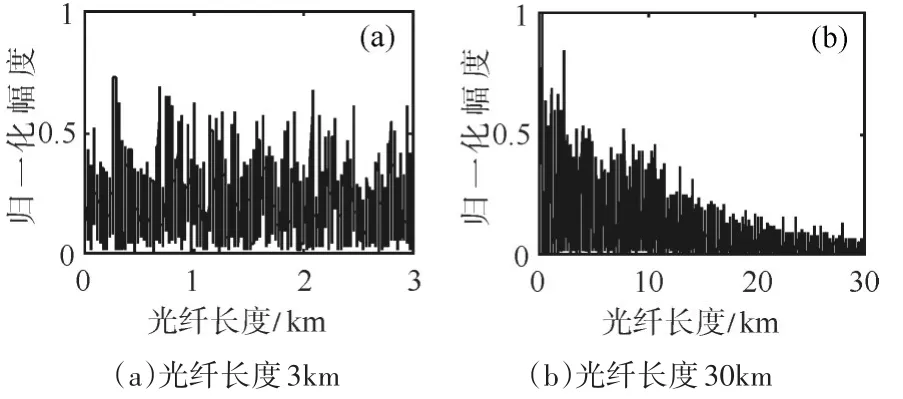
图3 瑞利散射光功率分布曲线

4 信号处理

4.1 非均匀采样原理

设ϕ-OTDR的传感光纤长度为3km，则光波在光纤内往返需要的时间约为0.03ms。所以探测光脉冲的间隔时间需大于0.03ms，若设系统探测间隔为0.1ms，则相应的采样频率为10kHz。根据奈奎斯特采样定理，当系统等间隔采样时，其最高响应频率为采样频率的一半，即5kHz。当振动信号含有大于5kHz的频率分量时，振动信号的高频分量与低频分量会在频域发生混叠。如果对振动信号做离散傅里叶变换（DFT），会在频域产生伪值。为直观表述，这里设存在振动信号s（t），其表达式为

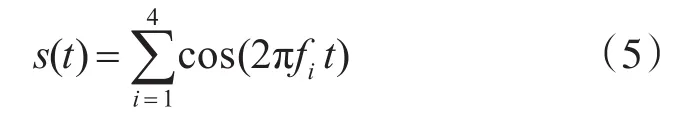
其中f1=3.2kHz，f2=22kHz，f3=68kHz，f4=94kHz，信号图像如图4（a）。若采用均匀采样且采样频率为10kHz，则可得采样后的信号如图4（b）。对采样后的信号做DFT可得频谱图如图5所示。可以发现，图中除了3.2kHz是真实存在的频谱分量，2kHz和4kHz处的频谱分量都是由于频率混叠而出现的伪值。

图4 信号时域曲线

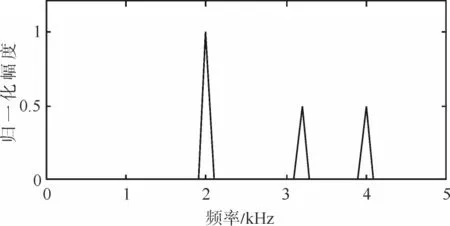
图5 均匀采样信号做DFT得到的频谱图

当振动信号在频域具有稀疏特性时，可以采取非均匀采样即随机采样的方法，突破采样定理的限制。此时采样间隔不再是固定值，而是一个时间范围。依然以式（5）中的信号s(t)为例，若采样间隔在［0.1ms，0.2ms］之间服从均匀分布，可得采样后的信号如图6所示。使用非均匀离散傅里叶变换（NDFT）求解其频域信号：

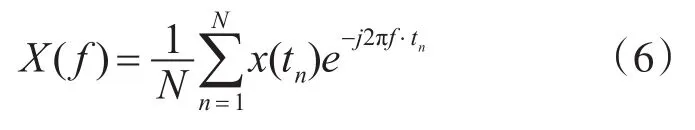
其中，x(tn)代表采样后的离散时域信号，N是总的采样点数。另外，NDFT方法的频域取值间隔fa与探测带宽B受采样点数N的限制，三者的最优关系式为［4］

其中，Nmin为最少采样点数。由式（7）可以看出，若想提高频率分辨率（即减小fa）或增大探测带宽B，必须要增大Nmin才能做到。但是Nmin增大也会相应增加系统的探测时延与运算量。若设B=100kHz，fa=100Hz，则采样点数至少需要N=250。图7（a）是当N=250时，随机采样信号经过NDFT后所得的频谱图。可以看到，图中四个较大的频谱分量正是原始信号s（t）中的四个频率。但是除了这四个频率值以外，还存在大量的干扰值，这是由于原始信号在经过NDFT时会发生频率泄露。由于频率泄露是均匀分布在整个频域上的，因而干扰值都比较小。且干扰值可以通过增加采样点数来进一步抑制。如图7（b），这是N=1000时的频谱图，可以看到干扰值显著减小了。

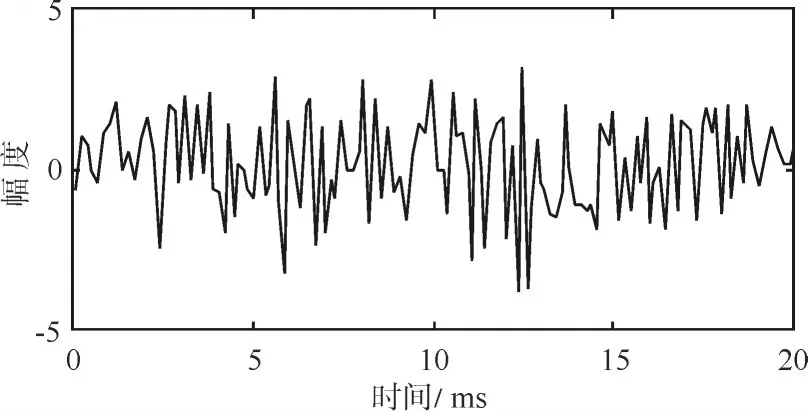
图6 随机采样得到的信号

图7 随机采样信号频谱图

4.2 信号处理与分析

为进一步研究随机采样方法应用到ϕ-OTDR系统时的情况，设光纤长度为3km，在2km位置处（取前后各5m共10m长光纤）加入一个频率与式（5）中s（t）相同，且折射率最大改变值为 6.5×10-5的振动。探测光脉冲间隔时间在［0.1ms，0.2ms］区间上服从均匀分布，仿真产生500条瑞利散射曲线，如图8所示。

图8 500条随机采样得到的瑞利散射曲线的叠加图像。

左边的图8（a）是无噪声条件下，振源附近500条瑞利散射曲线的叠加图，可以在2km处观察到振动造成的曲线振幅的改变。但是，实际的ϕ-OTDR系统中存在着背景噪声，而且噪声会随着时间累积变得越来越严重［11］。这里定义仿真信噪比（SSNR）为散射曲线均值与噪声功率均值的比值，在图8（a）曲线中加入SSNR=10dB的噪声，如图8（b）。可以看到在加入噪声后，已经无法分辨出振动点。

利用这500条瑞利散射曲线（SSNR=10dB），我们可以在光纤链路的每一点上都得到一个N=500的随机采样信号，代入式（6）即可求出各个位置处的频谱图。已知噪声信号在频域不具有稀疏性，如果仅仅是去掉几个比较大的频率分量，并不会改变信号的标准差。但是振动信号在频域具有稀疏特性，即除了几个比较大的频率分量外，其余频率分量都比较小。所以如果去除掉这几个比较大的频率分量，则信号的标准差会发生较大的改变。利用这一变化，就可以定位振动源的位置。在这里我们提出一种阈值法来得到各位置处的较大的频率分量［12］，阈值定义如下：

其中，α是频域信号的均值，Nf是频域采样点数。若所求频域带宽为100kHz，频率分辨率取fa=100Hz，则Nf=1000。利用阈值T，我们可以将频域信号中大于T的频率分量数目设为KT，KT≪Nf而且各位置处KT值会随信号频率大小自适应调整，如图9（a）。

图9 （a）光纤各位置处KT的取值；（b）利用信号标准差改变值得到的定位图像；（c）信号经移动平均法处理后的定位图像；（d）两种方法的信噪比对比图

将各位置处的KT个较大的频率分量去除，并计算去除前后该位置处频域信号标准差的改变值，将求得的改变值归一化后绘成曲线如图9（b）所示。可以看到，在2km位置处存在峰值。

将2km位置处的峰值与其他位置处的最大值之比定义为定位信噪比（LSNR），则可得图9（b）中的LSNR=14.3dB。这一结果是在SSNR=10dB的情况下得到的。将这一结果与传统ϕ-OTDR系统的信号处理方法进行对比，绘制出相同噪声条件下，传统的移动平均法［5］得到的定位图像，如图9（c），图中的LSNR=3.4dB。对比两种方法的抗噪性能，得到它们的LSNR与SSNR的关系图，如图9（d）。图中散点是五次结果取平均后得到的，相应的拟合曲线为5阶拟合曲线。其中实心黑点是利用标准差改变值定位时得到的LSNR值，而空心圆圈则是利用移动平均法定位时得到的LSNR值。由图9（d）可得，本文所提定位方法应用于随机采样信号时优于传统的移动平均法。而且当SSNR=0时，这一方法的LSNR值依然大于0，说明这一方法具有较好的抗噪性能。

定位振源位置之后，就可以求出相应的振动频率。为了求解准确，将图9（b）中峰值处求得的频域信号相加取平均，并利用式（8）找出其中大于阈值的频率分量，可得振动信号频谱图如图10（a）所示，其中明显突出的四个频率分量就是我们要求的频率分量。

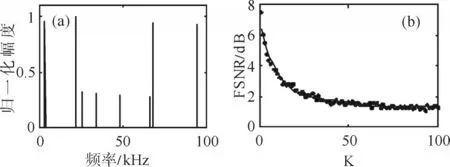
图10 （a）振动位置处的信号频谱图；（b）FSNR与信号频域稀疏度K的关系图

最后需要指出，随机采样求振动信号的方法也有其局限性，那就是只能求频域符合稀疏特性的振动信号。设振动信号的频域峰值与干扰值峰值之比为频率信噪比（FSNR），且设振动信号的频域稀疏度为K。FSNR与K之间的关系如图10（b）所示，图中散点是十次结果求平均得到的均值，曲线是对应散点的5阶拟合曲线。由图可知，若想得到FS⁃NR较高的频谱图，K应该越小越好。当振动信号中的频率分量大于10时，信号处理结果存在较大干扰。

5 结语

基于非均匀采样方法的ϕ-OTDR系统，可突破奈奎斯特采样定理对系统最高响应频率的限制，但是由于这一方法需要随机调制系统探测脉冲的间隔时间，所以传统的信号处理方法，如移动平均法应用于此处效果并不理想。针对这一问题，本文提出了一种利用离散频域信号标准差的改变值来定位振源的方法，通过设计仿真模型，对其抗噪性、信号频域稀疏度等方面进行了研究，并与传统移动平均法进行了对比。从仿真结果来看，对于具有频域稀疏特性的振动信号，本文方法的定位效果与抗噪性能都要优于传统的移动平均信号处理方法。这对于基于非均匀采样方法的ϕ-OTDR系统的进一步优化与应用有重要意义。