图文公式并用法在速度瞬心讲述中的应用*

张佃平，张 波，苟宁年，高广娣，尚 欣，曲爱丽

(宁夏大学机械工程学院，宁夏 银川 750021)

《机械原理》课程作为机械类专业的核心课程，主要内容包含机械的结构、运动、受力和动力学分析，特别对于化工机械中比如泵类、空气压缩机等机器尤为重要。但是，由于课程中概念较多，并且有些概念比较抽象，这就使得学生在学习这些概念的过程中存在较多的困难，表现在对概念的理解不深，应用无从下手。再就是，有些概念在大学物理、理论力学中已经学习，但是再引入《机械原理》一些新的概念后，学生并不能很快的理解，分析原因发现，学生在前修课程学习这些概念的时候本身就没有很好的掌握，加上对新学概念又理解不深，造成问题叠加。为了解决学生在机械原理课程中概念学习中掌握不够全面和深入的问题，笔者在教学的过程中尝试通过语言描述、图形表达和公式推演等多种手段进行讲解，通过多届学生的学习效果来看具有很好的成效。本文以机械原理课程中的速度瞬心这个概念为例来展示这一教学方法的运用，希望这种讲述方式能够给机械原理的概念讲解带来一定的启示。

1 概念引入

速度瞬心这个概念在《机械原理》课程的机构运动分析这一部分出现，主要是用于表述机构中两构件的速度关系，并且通过这种速度关系由速度已知构件对未知构件进行速度求解。但是速度瞬心对于学习机械原理课程的学生来说不是第一次接触，在前修课程《理论力学》中已经进行了学习。

在《理论力学》[1-3]中速度瞬心是基于平面图形来定义的。如果平面图形的瞬时角速度ω≠0，则平面图形上唯一地存在一个速度为零的点，该点称为瞬时速度中心，简称速度瞬心。如图1所示。

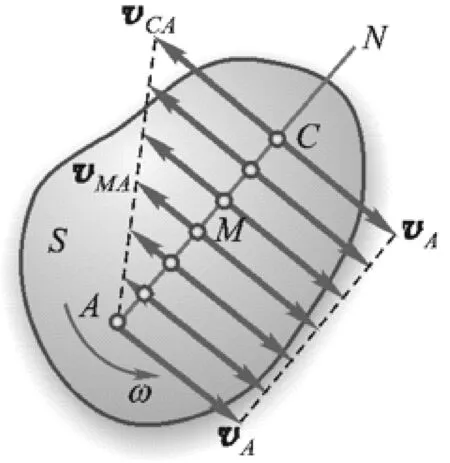
图1 平面图形速度瞬心示意图Fig.1 Schematic diagram of velocity instantaneous center

2 讲述思路

大多数《机械原理》[4-6]教材中对速度瞬心的定义为：两个作平面运动构件上速度相同的一对重合点，在某一瞬时两构件相对于该点作相对转动，该点称瞬时速度中心。从这个概念的描述来看，与《理论力学》所学习的速度瞬心的定义没有本质的区别，不同的是定义中引入了《机械原理》的概念—构件，综合了运动学的平面运动和转动知识。笔者在讲述这个定义的时候，发现有些同学对这个定义理解起来有些困难，普遍觉得其比较抽象。为了使学生能够较好的理解这个定义，并且为后续能够利用速度瞬心来解决速度求解的问题，在此定义讲解的过程中尝试从理论力学速度瞬心部分切入，采取语言描述、图形演示和公式表达的方式进行独自讲解与相互穿插讲述的方式进行授课，从学生的反馈来看收到了较好的效果。

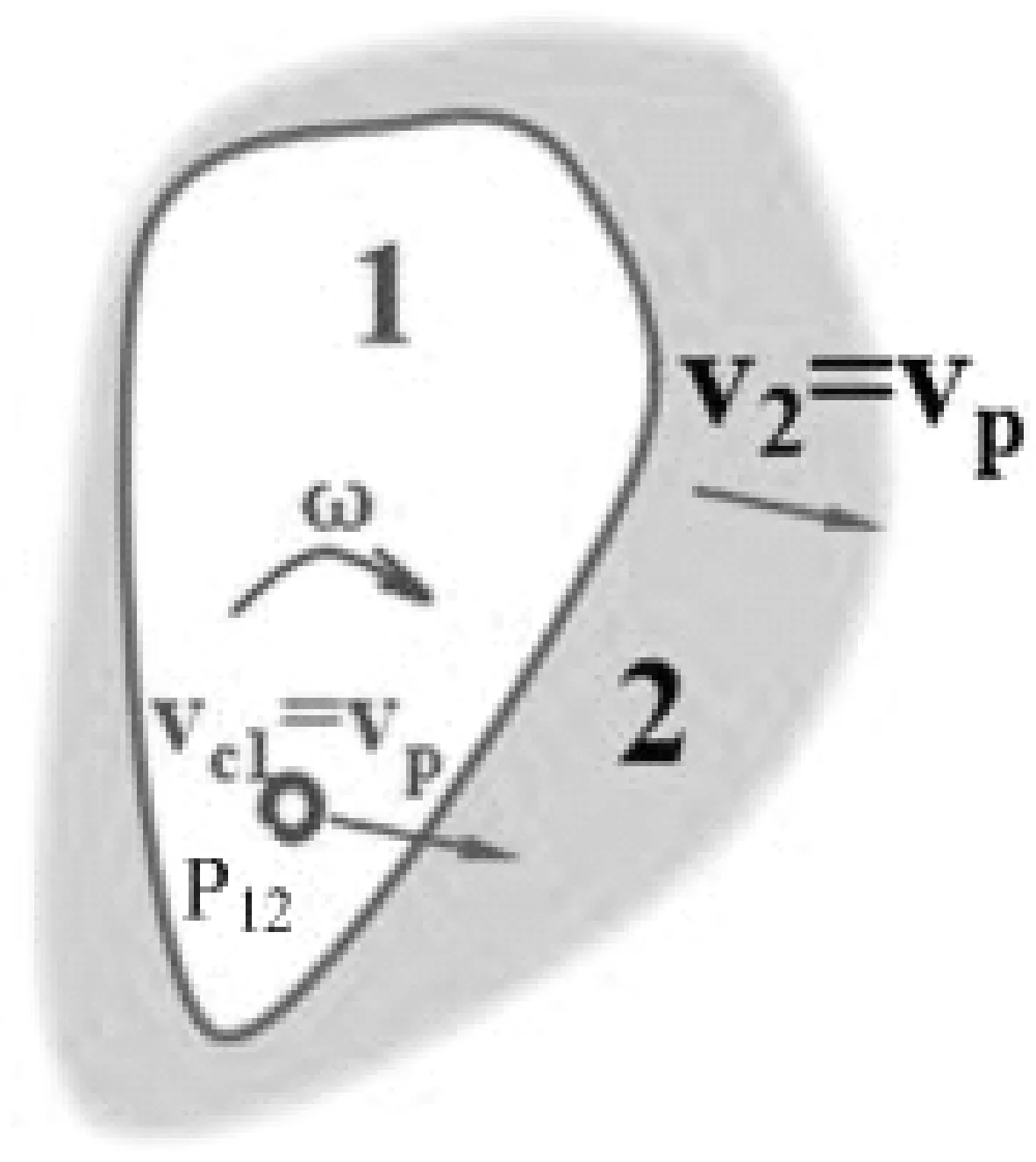
图2 两构件速度瞬心示意图Fig.2 Schematic diagram of velocity instantaneous center of two components

首先是回顾《理论力学》中速度瞬心的定义，通过对原有知识的描述使学生真正理解，速度瞬心是对平面图形(瞬时角速度ω≠0)上某一点的速度描述，记为P点，且在这一点处该物体的速度为零，即vp=0。为了讲述《机械原理》中速度瞬心的定义，此处需要扩展的是，引入另外一个平面图形，先使这个图形处于静止。对讲述内容中涉及的运动对象进行重新定义，原平面图形为构件1，静止的平面图形为构件2，在某一瞬时，则构件2与构件1上P点重合的点速度相等，都为零。再进一步，如果给构件1和构件2添加相同的速度，则对于两个运动的构件1和构件2来说，由于构件1和构件2的转动角速度不相同的认为是在平面内做平面运动，C点处的平动速度为vC1=vp，转动角速度不变，为ω，构件2认为在同一平面内做平动，速度为V2=Vp。所以，构件1和构件2速度瞬心的概念就顺理成章的描述为：在平面内运动的两个构件1和2，在某一瞬时，总可以找到一个速度相同的点P，并且这两个构件在这一瞬时绕着P点转动，此时，构件1和2的速度瞬心记为P12。用公式可以表示成Vp1=Vp2，ωp1≠ωp2。也就是说，速度瞬心在机构运动过程中是关于两个构件的一个特殊点，在这个点处这两个构件速度相同，并且绕着这个点做相对转动，这样就可以利用速度瞬心的定义进行速度的求解。速度瞬心用图2表示如下。

3 速度瞬心的应用

由前述可知，不管是在平面内对单个物体进行速度瞬心的定义还是针对于两个做平面运动的构件，速度瞬心的本质并没有变，即，速度瞬心是用来描述物体(构件)运动速度的一个点。由图2可以看出，构件1和2的速度瞬心为点P12，它所表示的物理意义是，在点P12处构件1和构件2速度相同，换句话说，已知构件1的运动情况，可以借助构件1和构件2在点P12处速度相同来求解构件2的速度，同时，还可以利用在这一瞬时构件1和2绕P12转动求解相应构件上任一点的速度，这就是速度瞬心在机构中速度分析的应用。如果推广到一般，就是如果有构件i和构件j，已知构件i的速度，要求求解构件j的速度，只要求解出构件i和构件j的速度瞬心Pij，借助构件i和构件j在Pij处相同就可以求出构件j的速度。

4 结 语

通过综合运用语言描述、公式表达和图形示意相结合的方式可以从不同的角度对同一概念进行解读，使学生能够从不同的方面加深对概念的理解，直至掌握概念，可以利用概念来解决问题。通过多个学期的教学情况来看，这种通过不同的角度对同一概念进行阐述的方式可以收到事半功倍的效果。