带凸资源和恶化效应的单机松弛窗口排序
姜昆
(汕头职业技术学院 自然科学系,广东 汕头515078)
0 引言
排序是组合优化问题,具有重要的理论和现实意义。一直是国际上的研究热点问题之一。经典的排序问题假定工件(也叫任务)的加工时间为给定常数,但在实际的生产过程中,工件的实际加工时间可能与开工时间(即恶化工件,参见文献Ng等[1],Wang和Wang[2],王吉波等[3,4],王吉波和赵伯来[5],Gawiejnowicz[6])和所用的资源(即资源约束或可控加工时间问题,Shabtay和Steiner[7],Lu等[8],罗成新和翟雯瑾[9])有关。比如,在钢铁制造企业的连铸轧制生产过程中,炼钢的基本单元是炉次,它是指同一座转炉一次共同冶炼的钢水。在炼钢的连铸阶段,高温熔融钢水在连铸机底部连续凝固成钢坯。当等待时间增加时(即加工开始时间延后),在连铸机上加工的炉次的温度将会降低,从而造成炉次加工时间的恶化(刘鹏等[10])。在另一方面,在给炉次的加热过程中需要资源(比如煤炭、电、天然气等),显然所用的资源越多,温度达到期望的时间就越短,从而出现有关恶化效应和资源约束典型的排序问题。
Wei等[11]讨论了工件具有恶化效应和资源约束的单机排序问题,其加工时间为开始时间和资源分配量的线性函数pj=aj+bSj-cuj,其中aj>0为工件Jj的基本(正常)加工时间,uj>0为分配给工件Jj的资源量,Sj≥0为工件Jj的开始加工时间,b≥0是恶化率,c≥0是给定常数。用三参数表示法,Wei等[11]证明了问题1|pj=aj+bSj-cuj|F是多项式时间可解的,F∈{δ1Cmax+δ2TC+δ3TADC+δ4gjujδ1Cmax+δ2TW+δ3TADW+,gj>0为资源量uj的单位费用,δ1≥0,δ2≥0,δ3≥0,δ4≥0是给定常数(由决策者给出),Cmax(TC,TW,TADC,TADW)为最大完工时间。Wang和Wang[12]研究了工件同时具有恶化效应与凸资源约束的单机排序问题,即加工时间为开始时间和资源分配量的凸函数pj=+bSj,其中wj为工件Jj的加工时间参数,k是给定的正数。Wang和Wang[12]证明了问题1|pj=+bSj|F,F∈{δ1Cmax+δ2TC+δ3TADC+δ4gjuj,δ1Cmax+δ2TW+δ3TADW+}是多项式时间可解的。Wang和Wang[13]研究了以文献[11]和[12]为基础的工期指派问题,Wang和Wang[13]证明了问题1|A|Ej+βTj+γdj+gjuj),A∈{pj=aj+bSj-cuj,pj=+b S j}对三种指派模型(即共同工期(dj=d)指派,松弛工期(d j=pj+q)指派,不同工期指派)是多项式时间可解的,其中dj为工件Jj的工期。在另一方面,Zhao等[14]研究了总资源消耗量有限的问题1|pj=+bSj,∑uj≤U|F(其中U是给定的总资源消耗量的上界,F∈{Cmax,TC,TADC,TADW,Ej+βTj+γdj),(αEj+βTj+γd+δD)},d为窗口的开始时间,D为窗口的长度),他们证明了这些问题都是多项式时间可解的。郭苗苗等[15]研究了Zhao等[14]的反问题,即问题1|pj=+bSj,F≤V|(其中V是给定的排序费用的上界,F∈{Cmax,TCTW,TADC,TADW,(αEj+βTj+γd j)(αEj+βTj+γd+δD)},他们证明了这些问题都是多项式时间可解的。
在准时制(Just-In-Time)的生产过程中,一般考虑共同的窗口指派问题,但为了更柔性的安排交货期窗口,Wu等[16]和Li等[17]研究了工件具有松弛窗口指派(具体定义见下面的模型描述)的排序模型。受文献Zhao等[14]、郭苗苗等[15]和松弛窗口的启发,我们研究在松弛窗口下的工件同时具有恶化效应和凸资源约束的排序问题,目标是确定工件的最优排序、最优的资源分配和松弛窗口的位置和长度使总资源消耗费用(排序费用)小于或等于给定常数的条件下,最小化排序费用(总资源消耗费用),并且证明这两个问题是多项式时间可解的。
1 问题描述
带有凸资源和恶化效应的松弛窗口排序问题可描述为:设有零时刻到达的n个工件J1,J2,…,JN要在一台机器上加工,所有工件加工过程中不能中断。同Zhao等[14]和郭苗苗等[15]一样,假设工件Jj的实际加工时间p为

其中wj为工件Jj的加工时间参数,uj为分配给工件Jj的不可更新资源的消耗量。每一个工件Jj都有一个交货期窗口[],,工件在这个交货期窗口内完工不受到惩罚。令Cj表示工件Jj的完工时间,Ej=max{0与Tj=max{0,Cj-}分别代表工件Jj的提前时间与延误时间。松弛窗口指的是=pj+q1,=pj+q2,其中q1和q2是松弛决策变量。本工作首先是研究所有工件的最优排序、最优资源分配和松弛决策变量q1和q2使得在总资源消耗费用有上界限制的情况下使工件的提前时间、延误时间、窗口的开始时间和窗口长度的线性组合最小,即问题:
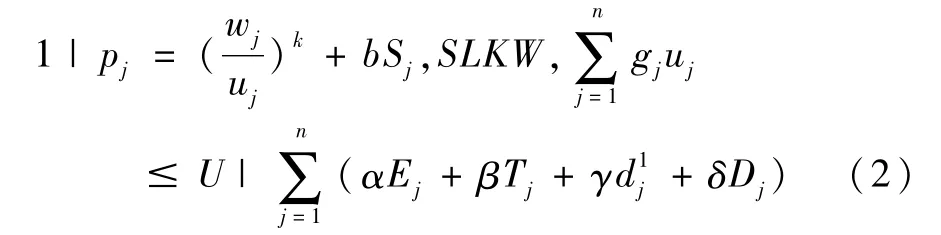
其中U表示总资源消耗费用的上界,SLKW表示松弛窗口指派模型。本文的第二个问题是研究第一个问题的反问题,即确定所有工件的最优排序、最优的资源分配和松弛决策变量q1和q2使得在工件的提前时间、延误时间、窗口的开始时间和窗口长度的线性组合有上界限制的情况下极小化总资源消耗费用,即问题:其中V表示工件的提前时间、延误时间、窗口的开始时间和窗口长度的线性组合的上界。

2 模型分析与求解

引理1存在一个最优排序,其中第一个工件的加工时间为0,并且相邻工件之间没有空闲时间。
引理2(Wu等[16])对任意指定排序,都存在一个最优排序使得q1和q2分别等于第h和第l个工件的完工时间,q1=C[h],q2=C[l],其中l≥h,

引理4(Wang和Wang[12])对于实际加工时间为pj=+bSj的模型,排在第j个位置的工件的实际加工时间为
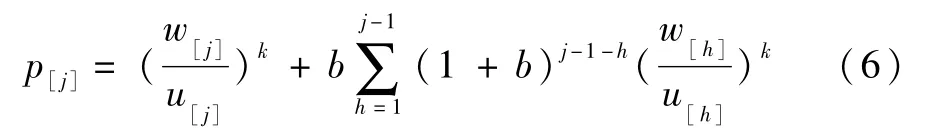
引理5(Hardy等[18])式子的最小值由xj的最大值与yj的最小值相乘,xj的次最大值与yj的次最小值相乘,依次类推得到。

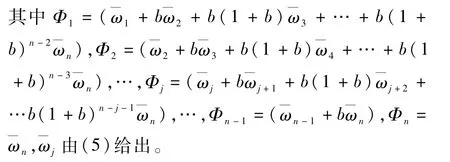
定理2问题1|pj=+bSj,SLKW,≤(αEj+βTj++δDj)的最优排序能够在O(nlogn)时间内得到。
由定理1和定理2,问题1|pj=+bSj,≤(αEj+βTj++δDj)的最优算法可以如下给出:
算法1
步骤1初始化参数:输入数据wj,gj(j=1,2,…,n),b,k,n,α,β,γ,δ,U;
步骤2计算最优位置
步骤3最优排序:计算(和(=1,2,…,n,由定理2得到工件的最优排序;
步骤4最优分配资源:由式(7)计算出对应最优排序的最优资源分配;
步骤5计算最优位置完成时间:计算q1=C[h],q2=C[l];
步骤6计算最优目标函数值:计算出排序目标(αEj+βTj++δDj)。
显然,算法1的步骤1)需要常数时间,步骤2)需要O(nlogn)时间,步骤3),4)和5)分别需要O(n)时间,因此算法1总的时间复杂度为O(nlogn),即问题能够在多项式时间O(nlogn)内解决。

定理3对于问题1|pj=+bSj,SLKW,最优的资源分配量为

定理4对于问题1|pj=+bSj,SLKW,βTj++δDj)≤V| gj uj,最优的排序能够在O(nlogn)时间内得到。
由定理3和定理4,问题1|pj=+bSj,,(αEj+βTj++δDj)≤V| gjuj的最优算法可以如下给出:
算法2
步骤1初始化参数:输入数据wj,gj(j=1,2,…,n),b,k,n,α,β,γ,δ,V;

步骤3最优排序:计算(和(=1,2,…,n,由定理4得到工件的最优排序;
步骤4最优分配资源:由式(8)计算出对应最优排序的最优资源分配;
步骤5计算最优位置完成时间:计算q1=C[h],q2=C[l];
步骤6计算最优目标函数值:根据式(14)计算出排序目标gjuj。
类似于算法1,算法2的总时间复杂度为O(nlogn),即问题能够在多项式时间O(nlogn)内解决。
3 算例

例1令n=6,b=0.05,k=2,α=9,β=12,γ=5,δ=7,U=200,V=300,w1=12,w2=13,w3=10,w4=8,w5=22,w6=11,g1=6,g2=7,g3=3,g4=4,g5=2,g6=5,所有数据保留7位有效数字。
解根据算法1和2,
步骤2h=1,l=2;
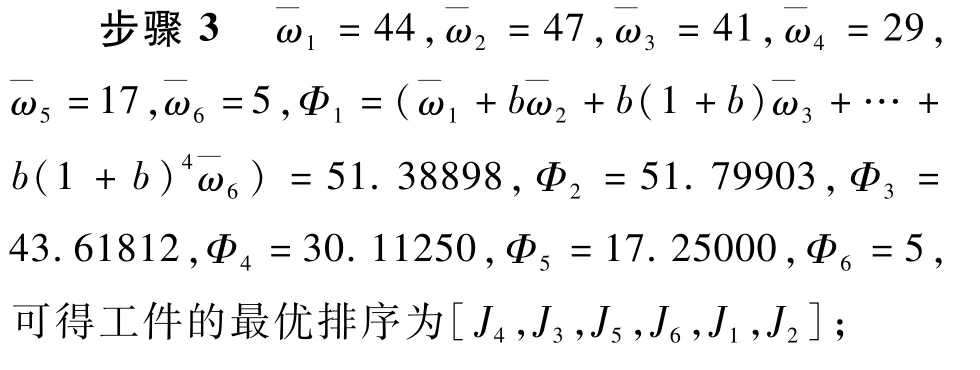
步骤4由式(7),问题的最优资源分配为:

步骤5q1=C[1]=C4=1.064500,q2=C[2]=C3=2.132008;

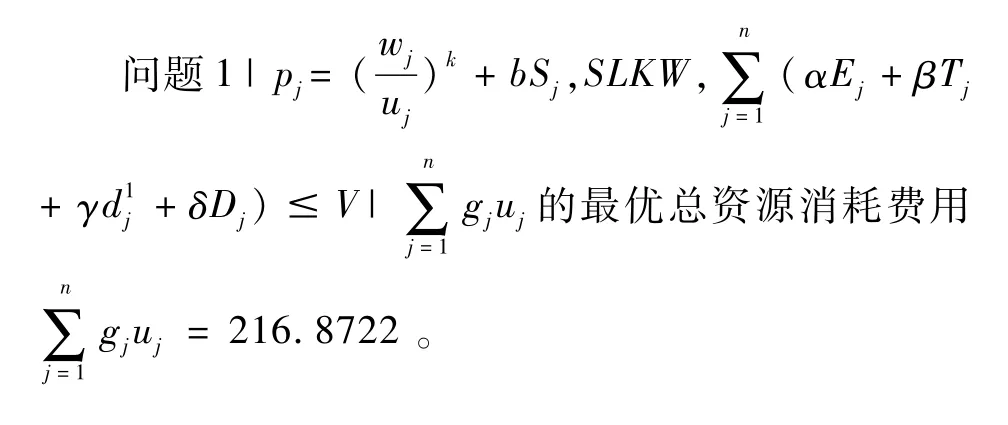
4 结论
考虑了工件带有凸资源和恶化效应的单机松弛窗口排序问题。目标是确定最优排序,最优的资源分配以及窗口的开始时间与长度,使总资源消耗费用(与窗口有关的排序费用)小于或等于给定常数的条件下,最小化与窗口有关的排序费用,证明上述问题都是多项式时间可解的。对其它机器环境(比如平行机或流水作业机)和其它目标函数的相关问题将继续研究。

