一种基于Kriging模型加点策略的多目标粒子群优化算法
陈 静, 唐傲天, 刘 震, 徐 森, 曹晓聪
(1. 吉林大学 汽车工程学院, 长春 130022; 2. 一汽轿车销售有限公司, 长春 130013)
在工程实践和研究中存在许多使多个目标在设计区域上尽可能最优的多目标优化问题(multi objective optimization problems, MOP), 以及求解或实验成本很高的多目标优化问题(expensive multi objective optimization problems, EMOPs). 近年来, 由于粒子群优化算法(particle swarm optimization, PSO)在多目标优化问题中具有协调多个目标的作用, 因此多目标粒子群优化(multi objective particle swarm optimization, MOPSO)被广泛应用于工程实践中[1], 目前已取得了许多研究成果. 孙小强等[2]采用聚类算法裁剪非支配解, 提高了解的分布性; 郭玉洁等[3]提出了一种双种群协同多目标粒子群优化算法, 通过双种群协同进化策略扩大搜索空间, 提高算法的全局搜索能力, 并结合Lévy飞行保证了种群多样性; 韩红桂等[4]提出了一种可提高多目标粒子群算法优化解的多样性和收敛性的MOPSO, 提高了计算速率. 但上述算法在收敛性方面, 特别是解决高维多目标问题或模型求解复杂问题上还有待改进. 刘华蓥等[5]采用网格拥挤距离与网格密度相结合的策略选取全局极值, 提出了一种基于空间划分树的多目标粒子群优化算法, 在保持种群多样性的同时提高了计算结果的准确性, 但该方法的估值仍有一定误差. 针对以上问题, 本文将多目标粒子群优化算法进行改进, 针对MOPSO提出一种基于Kriging模型的变异模式和基于Kriging模型的加点策略, 并将改进算法运用到多目标的Pareto最优解测试中, 取得了较好的效果.
1 多目标优化问题与Kriging模型
1.1 多目标优化问题的数学描述
当优化问题有m个目标函数、r个约束函数时, 其数学模型可表示为

(1)
其中:m>1为目标空间的维数;x=(x1,x2,…,xo)为o维设计变量;Ωo为x的可行解空间;f(x)为目标函数;gj(x)≤0为不等式约束条件. 由于MOP中各目标存在冲突关系, 无法使所有目标都实现最优, 因此只能协调考虑各目标, 寻求折中方案找到综合结果最优的解.
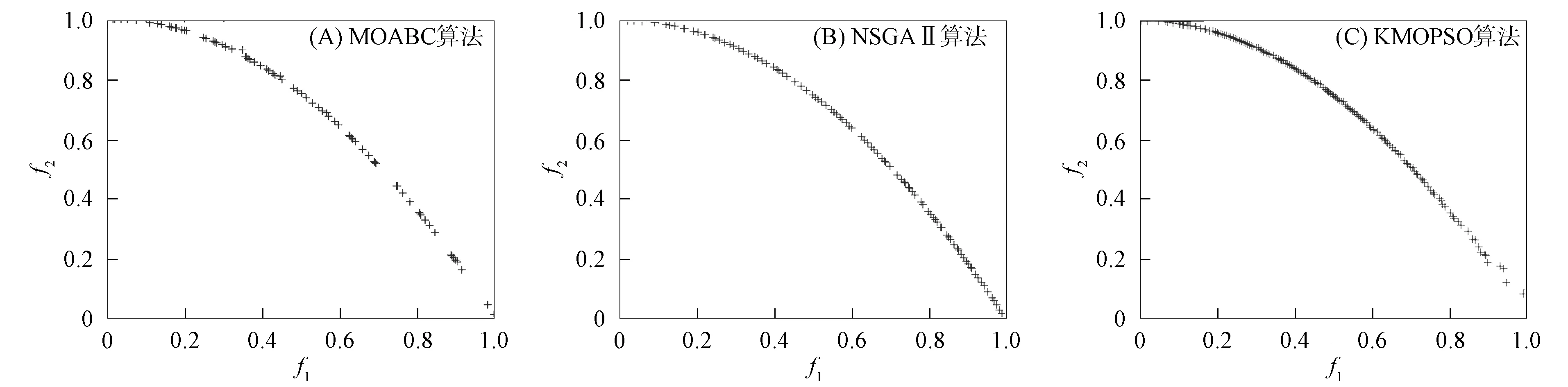
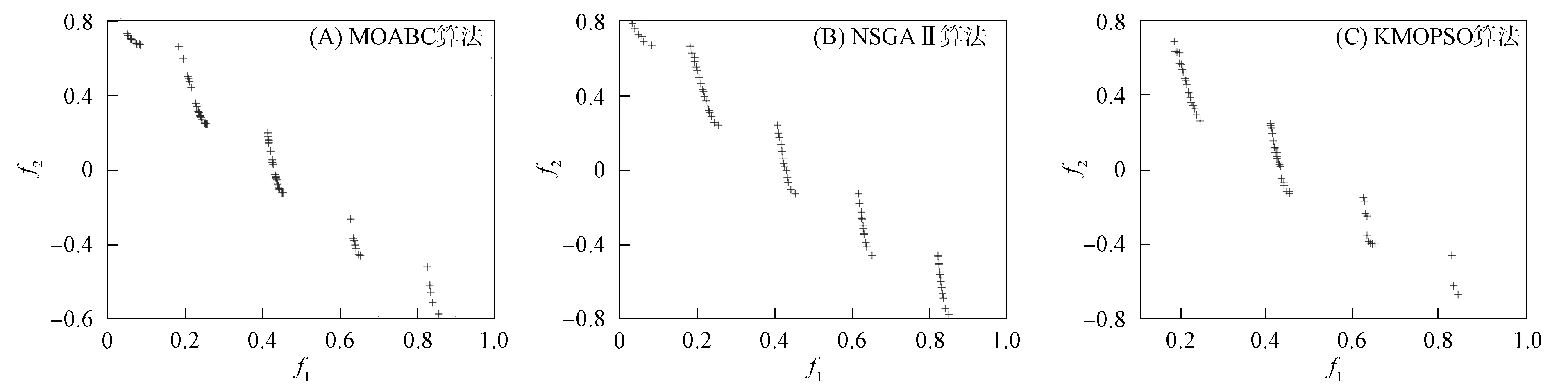
定义1(Pareto支配)[6]对于式(1), 假设有设计变量x(1),x(2), 满足fi(x(1))≤fi(x(2))(i=1,2,…,m), 且∃k∈{1,2…,m}, 使得fk(x(1)) 定义2(Pareto最优解)[6]对于式(1), 若不存在满足x(3)x(4)的设计变量x(3), 则称x(4)为非支配解或Pareto最优解. 定义3(Pareto最优解集)[6]可行解空间Ωo中所有Pareto最优解构成的集合称为Pareto最优解集, 记为Ps={x(5)|∃x(6)x(5)}. 定义4(Pareto前沿)[6]Pareto最优解集中所有Pareto最优解目标函数值形成的曲线(面)称为Pareto前沿, 记为PF={f(x)|x∈Ps}. Kriging[7]是一种基于高斯过程理论的元建模技术, 其不仅能精准预测未试验点的仿真响应值, 还能给出预测不确定性的度量, 在高维度、 非线性数学拟合方面表现优异, 对黑箱问题的解决有突出优势[8]. 设N次取样得到样本点{x(1),x(2),…,x(N)}的仿真结果为{y(1),y(2),…,y(N)}, 则Kriging模型可由下式表示: (2) (3) 其中:o为设计变量x的个数;θk,pk为待定系数,k=1,2,…,o, 其取值分别决定Ωo第o维的权重和平顺程度. 应用随机过程理论可得Kriging模型在未知点x处的预测值[10]: (4) 预测值的方差和偏导值信息分别为 (5) (6) 其中:R为样本点的N×N相关函数矩阵, 组成元素为 Rij=Corr[z(x(i)),z(x(j))]; r为未知点x与样本点间N×1的相关系数向量, 其中ri=Corr[z(x),z(x(i))];y是样本点响应值的N×1阶向量;1为各元素均为1的N×1列向量; 估算值 模型预测方差 对于粒子群算法[11-13], 要完成粒子速度、 位置更新过程中的自学习部分, 就要合理地选择一个局部领导者. 因此本文采用Pareto支配为主要准则, 基于Kriging模型设计一种快速支配的局部领导者更新策略. 用样本点及其目标函数值建立Kriging模型, 可获取目标函数f(x)=(f1(x),f2(x),…,fm(x))及约束函数g(x)=(g1(x),g2(x),…,gr(x)). 参考式(5)得到目标函数与约束函数预测值的误差函数分别为 (7) (8) 其中:k={1,2,…,m}表示第k个目标函数响应值;t={1,2,…,r}表示第t个约束函数响应值. 对粒子各历史位置的sfk(x)和sgt(x)值进行支配关系比较, 非支配粒子历史位置即为局部领导者. 在进行支配关系比较前, 先根据所有粒子历史轨迹的目标函数、 约束函数预测值的误差函数进行预处理, 剔除误差较大的粒子历史位置, 以提高搜索的准确性及效率. 若此时粒子的各历史位置互不支配, 则将各位置的误差函数进行比较, 选择误差最小的历史位置作为局部领导者. 大误差粒子历史位置剔除原则如下: 1) 根据式(7),(8)计算得到种群中所有粒子的sfk(x)和sgt(x)值, 先分别进行归一化处理, 再依次选取综合罚值Vi,m>0.95与Vi,r>0.975的粒子历史位置进行剔除; 2) 对多维度sfk(x),sgt(x)进行归一化处理, 综合考虑得到各维度的罚值分别为 (9) 通过 (10) 得到综合罚值Vi,m与Vi,r[14]. 其中:i表示粒子的历史位置;sfi,k表示目标函数为k时, 粒子当前位置的误差函数;sfmin,k与sfmax,k分别表示目标函数为k时, 粒子所有离历史位置误差函数的最小值与最大值;sgi,t,sgmax,t,sgmin,t定义参考sfi,k,sfmin,k,sfmax,k;ak与at分别为粒子第i个历史位置的目标函数和约束函数综合罚值中各维度罚值的权重. 2.2.1 储备解集的维护 随着迭代过程的进行, 越来越多的非劣质解通过支配关系比较被找到, 并储存在储备解集中. 当非劣质解数量达到储备解集的预设值上限时, 即需对储备解集进行实时维护, 即动态拥挤距离维护, 使种群能更准确地向PF搜索, 保证PF的合理性. 非劣质解的选取情形如下: 1) 在迭代过程中, 首先根据各粒子的误差函数进行大误差粒子的剔除, 再进行支配关系比较选择非支配解(非劣质解)进入储备解集; 2) 当储备解集中非劣质解的数量未达到预设上限时, 将所有非支配粒子全部储存到解集中; 3) 当储备解集中非劣质解的数量达到预设上限时, 需根据动态拥挤距离方法求解各非劣质解的拥挤距离值(crowding distance, CD)并排序, 去除掉CD值最小的一个粒子, 重复上述操作, 直到非劣质解的数量达到储备解集上限要求. 2.2.2 基于Kriging模型的变异机制 由上述非劣质解储备解的维护机制可知, 随着迭代次数的增加, 获取的非支配粒子数量也大幅度增加. 虽然动态拥挤距离可对储备解集进行维护, 但也会丢失部分最优解信息. 此外, 种群粒子的社会学习方式易导致算法出现早熟现象, 可能避开全局最优而使所有粒子陷入局部最优. 为尽量避免种群算法的早熟现象, 保证求解精度, 本文利用Kriging模型响应中的偏导值信息, 针对粒子群算法提出一种新的变异模式. 建立目标函数和约束函数的复杂程度函数cf(x)和cg(x)为 (11) 再进行归一化处理得到罚值Vcf和Vcg为 (12) 在对所有粒子的位置和速度进行更新时, 获取所有粒子约束函数的复杂程度函数值cg(x),对cg(x)=0的粒子进行变异处理; 同时对cg(x)≠0的粒子, 利用本文定义的罚值Vcg, 取Vcg<0.1的粒子进行变异. 粒子变异公式为 (13) 2.3.1 多目标EIMe准则及加点 在获取初始样本点后, 若进一步提高模型准确性, 则需获取新的样本点并进行更多的试验设计(design of experiment, DOE)实验, 以保证Pareto解集的前沿性. 但加点过程通常是盲目、 随机的, 需进行大量DOE实验才能达到期望的结果准确性. 为解决该问题, 在保证模型结果准确性的同时提高计算效率, 本文结合期望提高准则(expected improvement, EI), 提出一种基于Kriging模型的多目标粒子群优化算法的加点策略, 使DOE、 Kriging代理模型、 MOPSO这三者间形成信息的协调. 在维护后的储备解中获取每个非劣质解目标函数预测值的误差函数sfk(x), 可得每个非劣质解的置信度评估函数CEj为 (14) 得到上述信息后, 获取每个非劣质解基于Euler距离的期望提高准则值(expected improvement matrix, EIMe)[9]为 (15) 适应度函数的计算公式为 其中hkt为系数,k={1,2,…,m},t={1,2,…,r}. 2.3.2 收敛准则 当实现加点策略后, 新的样本点将被加入到初始点集中重新计算出新的Kriging模型, 并开始新一轮迭代过程. 只有当Kriging模型达到一定的模型精度后才能完成迭代, 输出Pareto前沿解集. 因此, 本文采用平均相对误差检验法验证模型的精度, 平均相对误差的计算公式为 本文改进的基于Kriging模型加点策略的多目标粒子群优化算法(KMOPSO)步骤如下: 1) 得到目标问题, 定义其设计变量、 目标和约束函数, 在初始设计空间中对复杂系统进行拉丁超立方试验设计生成初始样本点, 同时初始化种群; 2) 建立Kriging代理模型; 3) 大误差粒子剔除后进行支配关系比较, 非支配粒子进入储备解集, 完成储备解集的更新, 当储备解集中非劣质解达到上限时, 通过动态拥挤距离的计算进行储备解集的维护; 4) 找到粒子局部领导者与全局领导者, 然后进行粒子速度、 位置的更新, 同时利用构建的复杂程度函数进行变异处理完成粒子更新; 5) 对维护后储备解集中的非劣质解进行置信度评估函数的获取, 并得到近似Pareto前沿解集, 根据式(15)的期望准则从储备解集中寻找新的样本点加入原样本点集中; 6) 重复步骤1)~5), 直到满足收敛准则时完成迭代, 找到最优解. 针对提出的KMOPSO算法, 本文用综合指标(inverted generational distance, IGD)评价算法, 并采用多目标测试函数ZDT1,ZDT2,ZDT3,ZDT6[15]进行验证对比. IGD值表示算法计算出的近似与真实Pareto前沿解集之间的距离, IGD值大则表明近似Pareto前沿解集有较差的收敛性和多样性. IGD值的计算公式为 (18) 其中:P为均匀分布在PF上的点集, |P|为P的种群数量;Q为算法获取的最优Ps;d(v,Q)为P中个体v到种群Q的最小欧氏距离. 下面对本文算法与多目标人工蜂群算法(multi-objective artificial bee colony algorithm, MOABC)和多目标遗传算法(non-dominated sorting genetic algorithm Ⅱ, NSGAⅡ)进行对比实验. 算法参数设置如下: 种群数量为200, 储备解集大小为300, 学习因子c1=c2=1.5, 惯性权重ω=0.73, 变量维度设为10, 并分别独立进行10次计算, 所得IGD性能指标列于表1. 表1 IGD性能指标 由表1可见, 本文提出的KMOPSO算法在上述4个测试函数验证下, 其IGD指标的均值与标准差均小于另外两种对比算法, 即KMOPSO算法在高维问题下所得Pareto前沿解集最接近真实解集. 这是由于KMOPSO提出的加点策略更接近目标, 且粒子的变异模式也能更好地进行全局搜索. 图1 3种算法在测试函数ZDT1下返回的非支配前沿解集Fig.1 Non-dominated frontier solution sets returned by three algorithms on test function ZDT1 仿真结果如图1~图4所示, 其中包括ZDT1,ZDT2,ZDT3和ZDT6的非支配前沿解. 图1为测试函数ZDT1下3种算法返回的非支配解集. 由图1(A)可见, 使用MOABC算法得到的结果收敛性较差; 由图1(C)可见, KMOPSO算法的多样性比NSGAⅡ算法差, 但Pareto锋面的形状更好. 由图2~图4可见, 使用KMOPSO算法获得的结果具有理想的收敛性与多样性. 图2 3种算法在测试函数ZDT2下返回的非支配前沿解集Fig.2 Non-dominated frontier solution sets returned by three algorithms on test function ZDT2 图3 3种算法在测试函数ZDT3下返回的非支配前沿解集Fig.3 Non-dominated frontier solution sets returned by three algorithms on test function ZDT3 图4 3种算法在测试函数ZDT6下返回的非支配前沿解集Fig.4 Non-dominated frontier solution sets returned by three algorithms on test function ZDT6 综上可见, 本文提出的基于Kriging模型加点策略的粒子群优化算法, 首先利用Kriging模型的响应信息, 改进了粒子的变异模式以更好地解决粒子“早熟”问题; 然后在迭代过程的储备解集中选取非劣质解进入样本点集, 极大提高了计算结果的准确性; 最后提出大误差粒子剔除原则, 使支配关系比较的结果更精确. 仿真实验结果表明, KMOPSO算法可用于解决高维度、 非线性多目标问题, 且可利用较少的样本点得到更精确的代理模型, 在提高收敛速度的同时能较好地逼近Pareto前端.1.2 Kriging模型
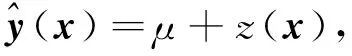



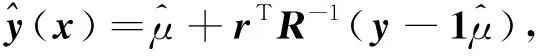


2 基于Kriging模型的多目标粒子群优化算法
2.1 局部领导粒子的更新策略

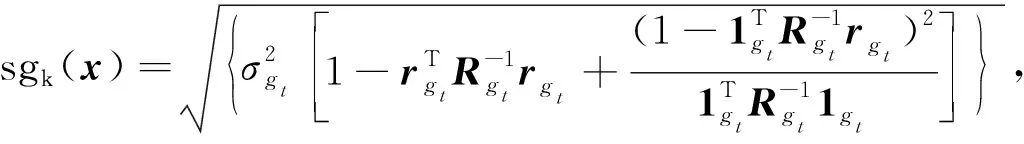
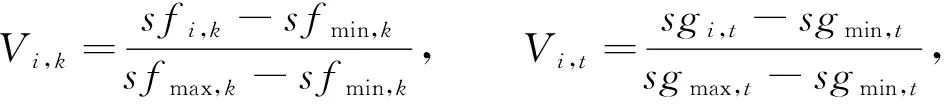

2.2 非劣质解储备解集构建机制





2.3 基于Kriging模型的加点策略

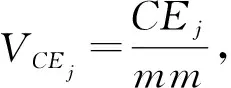


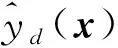
2.4 基于Kriging模型的粒子群优化算法求解多目标优化问题流程
3 算法性能测试
3.1 性能指标IGD

3.2 仿真验证及分析