带跳随机波动率模型的美式期权及美式障碍期权定价

薛广明, 林福宁

(广西财经学院 信息与统计学院, 南宁 530003)

1 引言与预备知识

期权定价是金融数学的研究热点, 按期权种类分为欧式期权和美式期权. 目前欧式期权已有很多定价模型[1-3]. 但美式期权定价相对复杂, 一般很难得到表达式, 只能通过数值方法给出近似表达式. 目前已有很多近似逼近的方法, 如二叉树、 有限差分法、 Monte Carlo模拟法等.

美式期权具有提前实施的权利, 因此已被广泛关注. Kou等[4]在跳跃扩散模型下, 利用二次逼近法研究了美式看跌期权价格的近似显示解; 邓国和等[5]在随机波动率与双指数跳跃扩散组合模型下研究了美式期权定价; 邓国和[6]在双跳跃仿射扩散模型下研究了美式看跌期权定价. 美式障碍期权不仅具有障碍期权的优点, 还具有提前实施的权利, 目前文献报道较少. Karatzas等[7]利用变分不等方程给出了美式上升敲出障碍期权的定价和套期保值策略; 霍海峰[8]在分数次布朗运动下研究了美式障碍期权定价.

百慕大期权(Bermuda option)是一种可在到期日前所规定的一系列时间行权的期权. Geske等[9]研究表明, 当百慕大期权的可执行点趋于无穷多时, 其价格的极限即可视为相应美式期权的价格; MacMillan[10]将文献[9]的方法应用到标的物为股票的期权定价研究中； Barone-Adesi等[11]应用文献[9]的方法研究了商品期货期权定价. 令Pi为含有i个可提前执行时间点的百慕大期权在零时刻的价格, 则P1等价于一个欧式期权, 即只能在到期日T时刻执行. 根据文献[9], 美式期权PA=P∞, 但对无穷多个可执行时间点的情形通常无法操作. Bunch等[12]研究表明, 通常情况下计算过程仅需有限步即可获取近似解. 用执行时间点个数分别为1,2,3的百慕大期权构造美式期权的近似公式为

PA≈2P2-P1,

(1)

(2)

式(1),(2)分别称为两点G-J法和三点G-J法. 本文基于文献[9], 在跳扩散随机波动率模型下, 利用百慕大期权的价格逼近美式期权的价格, 讨论美式期权定价和美式障碍期权定价.

2 模型假设

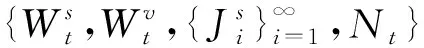
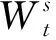
引理1[13]设n维随机变量X的分布函数是F, 如果其密度函数f和特征函数φ(u)都是Lebesgue可积的, 即f∈Ln,φ(u)∈Ln, 则对∀x=(x1,…,xn)∈n, 有

这里定义

其中:u=(u1,…,un)⊥;Δa[η(a)]=η(a)+η(-a). 根据n的奇偶性, 引理1可分为两种情形, 即

其中: Re[·]表示函数实部; Im[·]表示函数虚部; i为虚数单位.

若F为n维随机变量X的分布函数,t(·)满足引理1, 则对∀x=(x1,x2,…,xn)∈n, 有

3 美式期权定价

下面以美式看涨期权为例给出美式看涨期权的近似解, 由式(2)可知, 要计算出美式看涨期权的近似解, 就要先分别计算可执行时间点个数分别为1,2,3的百慕大障碍期权在0时刻的价格P1,P2,P3. 令K表示期权的执行价格,T表示到期日, 下面考虑只有一个可执行时间点百慕大期权在0时刻的价格, 即在到期日T时刻执行, 其等价于欧式看涨期权的价格, 即P1=Ce.

引理2[6]跳扩散随机波动率模型下标准欧式看涨期权0时刻价格为

(5)

其中:

于是

(6)

同理有

(7)

对于I3, 应用二维测度变换将测度Q变换到Q2, 其Randon-Nikodym导数为

于是

同理有

其中：

(10)

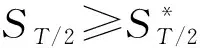
引理3在2个执行时间点T/2和T的跳扩散随机波动率模型下, 百慕大看涨期权的0时刻价格为

其中M1,N1,ψ2定义如式(10).

证明: 将式(6)～(9)代入式(5)可得结论.

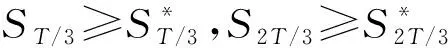
记P3为该期权的价格, 于是被限制的百慕大看涨期权的价值等于ST/3-K,S2T/3-K和ST-K分别在T/3,2T/3和到期日T时间点的折项期望之和, 即

其中:

下面根据引理1分别计算I5～I10. 对于I5, 类似求I1的过程, 应用测度变换可得

同理有

(12)

对于I7, 类似求I1,I3的过程, 应用测度变换可得

同理有

其中：

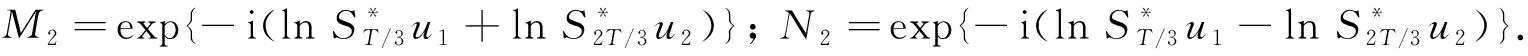
(15)

为方便, 先给出下式:

对于I9, 应用三维测度变换将测度Q变换到Q2, 其Randon-Nikodym导数为

于是

对于I11, 应用二维测度变换得

其中M2，N2定义如式(15).I12由式(16)可得. 同理有

其中M2，N2定义如式(15).I14由式(16)可得.

引理43个执行时间点T/3,2T/3,T的跳扩散随机波动率模型下, 百慕大看涨期权的0时刻价格为

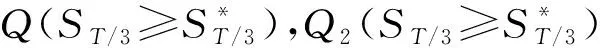
证明: 综合式(9)～(20)可得结论.

定理13个执行时间点T/3,2T/3,T的跳扩散随机波动率模型下, 美式看涨期权的0时刻价格为式(2).

证明: 由引理2～引理4及三点G-J法可得结论.

4 美式障碍期权定价

引理5对于执行时间点为到期日T时刻的跳扩散随机波动率模型, 百慕大下降敲出看涨障碍期权在0时刻的价格为

其中:

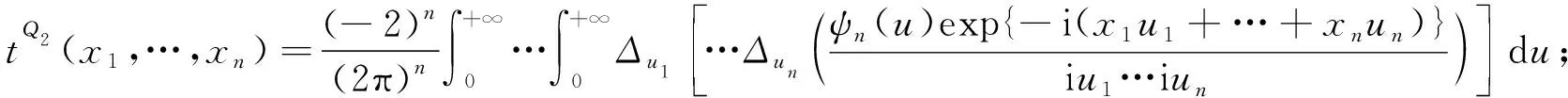
(21)

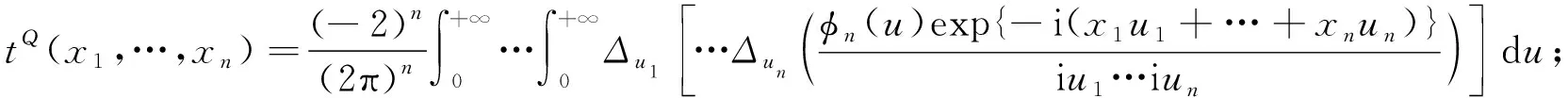
(22)

ψn(u1,…,un)表示在测度QS下的特征函数, 即

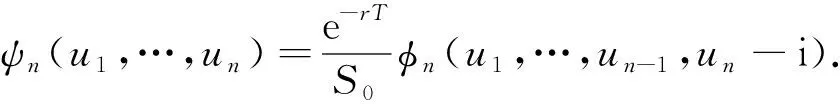
(23)

证明: 设障碍值SB=L为常数, 下面以S0>L>K为例证明. 考虑离散时间欧式下降敲出看涨障碍期权的价格, 根据风险中性定价原理知,

其中tQ(x1,…,xn)定义如式(22). 对于I15的计算, 应用二维测度变换同理可得

其中tQ2(x1,…,xn)定义如式(21),

其中:

下面分别计算I17～I20. 对于I17, 应用测度变换可得

其中

(26)

同理有

其中

(27)

(28)

对于I19, 应用测度变换同理可得

其中：

这里tQ2(x1,…,xn)定义如式(21);

这里tQ2(x1,…,xn+1)定义如式(26). 同理有

其中:

这里tQ(x1,…,xn)定义如式(22),ψn(u1,…,un-1,un)定义如式(23);

这里tQ(x1,…,xn+1)定义如式(27),ψn+1(u1,…,un,un+1)定义如式(28).

引理6在跳扩散随机波动率模型下, 对于2个执行时间点T/2和T的百慕大下降敲出看涨障碍期权的0时刻价格为

由引理5和引理6可得:

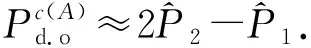
5 应用实例

下面应用数值方法分析跳扩散随机波动率模型下美式期权和美式下降敲出障碍期权权利金, 其中美式下降敲出障碍期权以K>L时为例, 计算软件选用MATLAB 7.0和Mathematica 5.0. 为便于解释和分析, 模型(3),(4)中的参数取值列于表1.

表1 模型(3),(4)的基本参数值

表2列出了跳扩散随机波动率模型下美式期权与美式障碍期权的价格比较, 其中参数取值见表1. 美式障碍期权的目的是把投资者的收益或损失控制在一定范围内. 由表2可见, 当参数取值相同时, 美式期权价格略高于美式障碍期权价格, 这与障碍期权的本质相符.

表2 跳扩散随机波动率模型下美式期权与美式障碍期权的价格比较

综上, 本文在随机波动率和股价满足跳扩散模型的环境下, 应用随机分析、 Fourier反变换等方法给出了美式看涨期权和美式障碍看涨期权的近似价格公式. 这类定价模型能较好地拟合金融实际数据中利率、 股价的运动行为, 捕捉金融市场中突发事件和波动的聚集性. 最后, 应用数值实例分析了美式期权与美式障碍期权的价格差异, 结果表明, 当参数取值相同时, 美式期权价格略高于美式障碍期权价格, 与障碍期权的定义相符.