具有变系数四阶抛物方程的B样条有限元法
秦丹丹, 唐鑫鑫, 黄文竹
(1. 空军航空大学 基础部, 长春 130022; 2. 吉林大学 数学学院, 长春 130012;3. 贵州医科大学 生物与工程学院, 贵阳 550025)
微分方程是一种常见的数学模型. 由于实际应用中很多问题不仅与空间变量有关, 而且受时间变量影响, 因此抛物方程尤其是高阶抛物方程在许多领域应用广泛. 如Cahn-Hilliard方程[1-3]被人们用于分析自然界中的扩散现象[4-5], 其形式如下:
ut+γΔ2u-Δf(u)=0,
其中f(u)在不同的问题中表达式不同.
由于很多微分方程无法找到解析解, 因此, 人们致力于研究微分方程的数值解法, 其中有限元方法是一种有效的方法. 关于Cahn-Hilliard方程的有限元法目前已有很多研究成果[6-11]. 针对带有梯度能量系数的黏性Cahn-Hilliard方程, Choo等[9]构造了有限元格式并进行了理论分析; Qin等[11]讨论了晶体表面生长模型的B样条有限元方法及其近似解的有界性和收敛性, 并通过数值结果验证了格式的有效性. 有限元方法本质上是利用分片多项式函数离散连续问题, 实现从无限维空间到有限维空间的转化, 因此, 有限维子空间基函数的选取至关重要. B样条作为一种分段多项式函数[12], 用于各种数值计算问题, 包括有限元分析[13-15]. 由于B样条具有紧支集且只有一族基函数, 可节省存储空间, 提高计算效率, 因此本文选取B样条作为有限元基函数.
1 模 型
本文取f(u)=-u, 并限定初边值条件, 为使模型的适用范围更广, 将常系数γ换成变系数, 得到模型:

(1)
这里I=[0,1]. 变系数α(x,t)满足连续性:

(2)
有界性:
0 (3) 以及关于时间变量偏导数的有界性: (4) 其中s,S,M是正常数. 基于边值条件, 定义函数空间 (5) 下面给出等距B样条对应卷积的定义. 定义1[11]设m为正整数,N1(x)为[0,1]上的特征函数, 则函数 称为m阶B样条. 本文考虑求解模型(1)的三次B样条有限元法. 定义剖分Ih: 0=x0 近似解uh(x,t)∈Uh可表示成 (6) 为分析B样条有限元格式解的有界性与收敛阶, 引入下列算子. a(u-Rhu,vh)=(α(x,t)D2(u-Rhu),D2vh)=0, ∀vh∈Uh, (7) 这里a(u,v)=(α(x,t)D2u,D2v). 由α(x,t)的性质(3)和椭圆投影算子的定义(7), 可知其为双线性的对称正定算子, 且满足式(7)的Rhu唯一确定, 并有如下估计[17]: ‖u-Rhu‖+h‖u-Rhu‖1+h2‖u-Rhu‖2≤Ch4‖u‖4. (8) 下面证明半离散问题解的有界性. ‖uh(t)‖2≤C‖uh(0)‖2, 0≤t≤T, (9) 其中正常数C仅与s,M,T有关, 与步长h无关. 证明: 问题(6)是一个常微分方程组, 因此, 它在区间[0,tn)上存在唯一的局部解. 若可以证明式(9)成立, 再结合拓展定理, 可得整体解的存在唯一性. 所以只需证明式(9)成立. 在问题(6)中, 取vh=uh, 由式(3)和内插不等式知, 易见 (10) 由Gronwall不等式, 可得近似解的L2模有界性: ‖uh(t)‖2≤et/s‖uh(0)‖2≤eT/s‖uh(0)‖2≤C‖uh(0)‖2, 0≤t≤T. (11) 对式(10)关于时间变量t积分, 得 (12) 将式(11)代入式(12), 得 (13) 在式(6)中, 再取vh=uh,t, 得 ‖uh,t‖2+(α(x,t)D2uh,D2uh,t)-(Duh,Duh,t)=0. 通过简单求导运算, 可得 由变系数的性质, 易得 关于变量t积分, 得 由ε-不等式可知 由式(11),(13), 可得近似解的H2半模有界性: ‖D2uh(t)‖2≤C‖D2uh(0)‖2, 0≤t≤T. (14) 又因为 所以‖uh(t)‖2≤C‖uh(0)‖2, 这里正常数C与s,S,M和uh(0)有关. 证毕. 下面给出半离散问题解的误差分析. 定理3设u和uh分别是弱形式(5)和半离散问题(6)的解, 且有u(0)∈H4(I),u,ut∈L2(0,T;H4(I)), 则当0≤t≤T时, 近似解的L2模有如下误差估计: (15) 其中正常数C仅与α(x,t)有关, 与步长h无关. 证明: 记θ(t)=Rhu-uh,ρ(t)=u-Rhu, 则u-uh=θ(t)+ρ(t), 从而 ‖u-uh‖≤‖θ(t)‖+‖ρ(t)‖. (16) 推导误差只需要估计‖θ(t)‖. 联立式(5)~(7), 得 (θt,vh)+(α(x,t)D2θ,D2vh)=-(ρt,vh)+(Dθ+Dρ,Dvh). (17) 在式(17)中取vh=θ, 则有 整理可得 (19) 由Gronwall不等式, 可得 由于 ‖θ(0)‖=‖u(0)-uh(0)+Rhu(0)-u(0)‖≤‖u(0)-uh(0)‖+‖ρ(0)‖, (21) 所以当0≤t≤T时, 结合式(20)和式(21)可知式(15)成立. 证毕. 定理4设u是弱形式(5)的解,uh是半离散问题(6)的解,u(0)∈H4(I),u,ut∈L2(0,T;H4(I)), 则半离散问题解的误差估计如下: (22) 这里正常数C仅与α(x,t)有关, 与步长h无关. 证明: 在式(17)中选取vh=θt, 则 ‖θt‖+(α(x,t)D2θ,D2θt)=-(ρt,θt)+(Dθ+Dρ,Dθt). 通过求导运算, 由ε-等式可得 基于α(x,t)的限制(4)和ε-不等式, 可得 整理可得 (23) 在式(23)两端关于变量t积分, 有 再利用α(x,t)的限制条件(3), 可得 由Gronwall引理知 (24) 注意到 ‖D2θ(0)‖≤‖D2u(0)-D2uh(0)‖+‖D2Rhu(0)-D2u(0)‖, (25) 联立式(24)和式(25), 有 再由式(16)可得式(22). 证毕. (26) 下面讨论全离散格式解的收敛性. ‖u(0)-u0h‖≤Ch4‖u(0)‖4, (27) 则有如下误差估计: (28) 其中C是一个仅依赖于α(x,t)的常数, 与时间步长Δt和空间步长h无关. (∂tθn,vh)+(α(x,tn)D2θn,D2vh)=(rn,vh)+(Dθn+Dρn,Dvh). (29) 令vh=θn, 则有 整理可得 ‖θn‖2-‖θn-1‖2+sΔt‖D2θn‖2≤CΔt(‖θn‖2+‖ρn‖2+‖rn‖2). 关于n求和, 可得 由投影Rh的性质和Hölder不等式知 从而可得rn的估计: (31) 将式(31)代入式(30), 当Δt足够小, 且CΔt<1-δ(0<δ<1)时, 有 利用式(8)和式(27)可知, ‖θ0‖≤‖u(0)-uh(0)‖+‖u(0)-Rhu(0)‖≤Ch4‖u(0)‖4. 考虑如下问题: (32) 这里α(x,t)=1+xt, 解析解取为u(x,t)=t2[1-cos(2πx)], 计算可得 g(x,t)=2t-16π3t3sin(2πx)-[16π4t3+(16π4-4π2)t2+2t]cos(2πx). 表1 当t=1时, 不同空间步长h对应的误差和收敛阶 表2 当t=1时, 不同时间步长Δt对应的误差和收敛阶 综上所述, 对于一类四阶项带有变系数的抛物方程, 本文通过构造B样条有限元法, 引入双调和椭圆投影算子, 讨论了半离散格式解和全离散格式解的收敛性. 数值算例很好地验证了理论结果. 与Hermite有限元法相比, B样条有限元法能节省理更大的存储空间, 运行速度更快, 而且能达到较好的收敛精度.
2 B样条有限元法
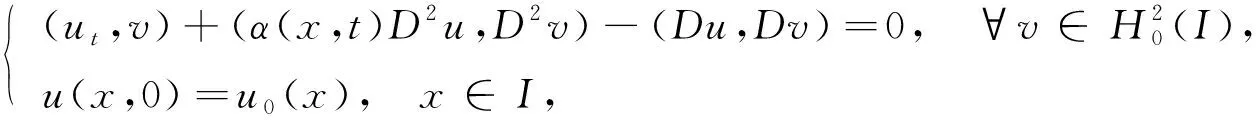



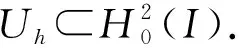
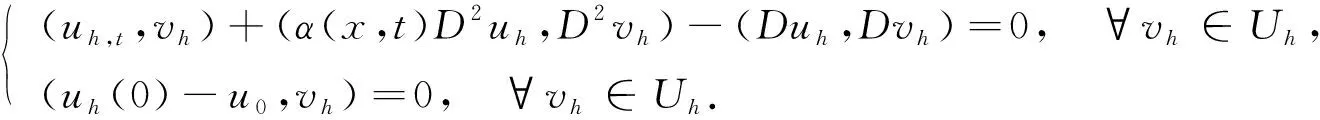
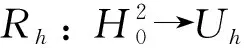
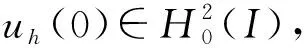
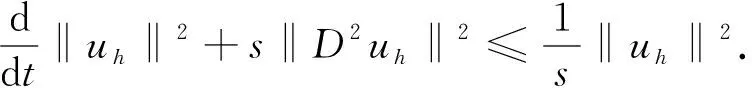






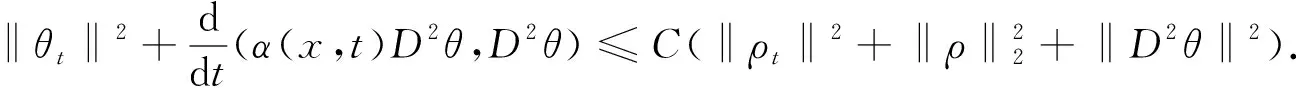
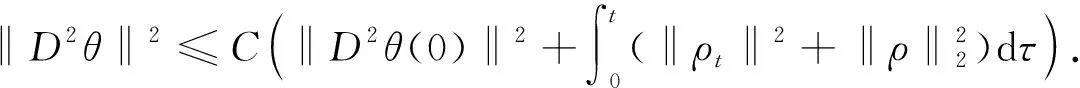
3 全离散格式

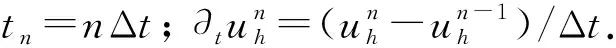


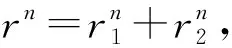


4 数值模拟





