任意阵列阵元缺损下的缺失数据恢复方法*
方启林
(中国科学技术大学,安徽 合肥 230022)
0 引言
阵列信号处理在雷达、导航和其他通信领域中得到了广泛运用,ESPRIT、MUSIC 等方法能精确估计来波角度。然而,随着阵列规模的不断扩大,整个信号处理过程中处理的数据量不断增加。当来波信号个数较少时,全采样整个阵列会产生冗余。因此,合理减少采样阵元数可以有效提高效率。另外,增加阵列规模会增大阵元损坏可能性,如果阵元发生损坏,DOA 估计精度将会受到影响。以上两种情况可以统一看作缺损的是对应位置上的阵元,接收数据矩阵出现缺失元素。如何解决接收数据矩阵的缺失元素的恢复问题具有重要的价值。
矩阵填充(Matrix Completion,MC)[1-2]理论是一种已知矩阵的部分元素,利用矩阵的低秩性重构出原始矩阵的有效方法。矩阵填充理论已经被运用于波达方向估计[3-4],取得了较好的结果。但是,在实际应用过程中,阵元缺损也许会使接收数据矩阵的某一整行的数据全部缺失,而一般的MC 理论需要采样矩阵至少存在一个非零元素的每一行或者每一列来保证重构的原始接收数据矩阵的准确性。所以,文献[5]将接收到的单次快拍列向量数据转换成等效低秩矩阵,再用MC 方法恢复缺失数据,但是因为只用到一次的数据,降低了估计精度。文献[6]对出现全零行的接收数据矩阵的每个列向量进行变换,变成一个Hankel 矩阵,再把得到的Hankel 矩阵重构成一个二重块Hankel 矩阵,然后采用MC 理论填充变换后的矩阵,利用反变换重构出完整的接收数据矩阵,获得了较高精度的角度估计值。然而,文献[5-6]都是针对均匀线阵提出的方法,如果是一般的阵列(如二维阵列、非均匀线阵等),这些方法将会失效。由于不能推广到二维阵列,它将无法同时实现对方位角和俯仰角的估计。
针对任意阵列结构的一般阵列且有部分阵元缺损的情况,在传统的MC 问题基础上引入子空间约束,构造了一个新的凸优化问题,通过求解凸优化问题,能够恢复出接收数据矩阵中的整行缺失的元素,同时能够实现对角度的有效估计。
1 信号模型和问题描述
假设空间中存在K个相互独立的窄带辐射源,它们的中心频率为f,波长为λ,接收天线数为M,任意一般阵列K<<M。忽略噪声时,在t时刻阵列接收到的信号向量为:


所以,阵列的接收数据矩阵可以看作是低秩的。一般地,会有一些噪声混入阵列天线接收信号,此时接收数据矩阵可以写成:

式中,N表示加性空时高斯白噪声。在噪声较小的情况下,可以认为接收的数据矩阵满足低秩性,依然可以用MC 理论对其进行分析研究[7]。
在有部分阵元缺损的情况下,缺损阵元将没有输出信号(输出为0),此时接收数据矩阵X的一些行的数据整行缺失。不失一般性,本文用XΩ表示有Mb行元素整行缺失的数据矩阵,下标Ω为矩阵X未缺失元素位置的集合,且满足M-Mb>K。现在问题是如何利用XΩ和X的低秩性求出原矩阵X,从而恢复出Mb行整行缺失的数据。
2 矩阵填充的基本模型
因为接收数据矩阵是低秩的,所以在XΩ有强不相干性[7](Strong Incoherence Property,SIP)时(如数据矩阵X的部分元素随机缺失,而不是整行缺失),则可通过秩最小化约束,利用缺失部分元素的数据矩阵XΩ重构出原始数据矩阵X。这个约束优化问题可以表示为:
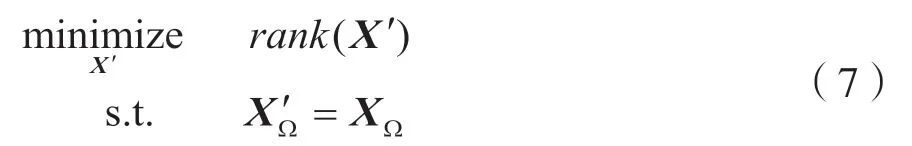
式中,X´∈RM×L为变量矩阵。问题(7)是秩最小化问题,求解是NP-hard 问题[8],因此通常将式(7)转化为求解约束凸优化问题:
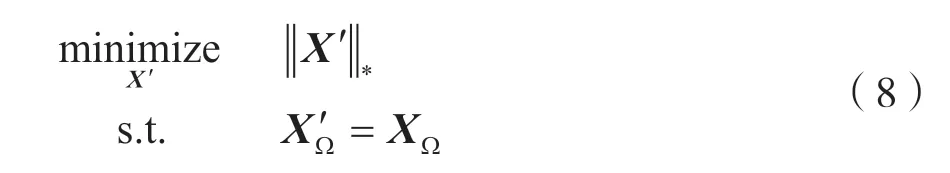
进一步,可以转化为解决无约束凸优化问题:
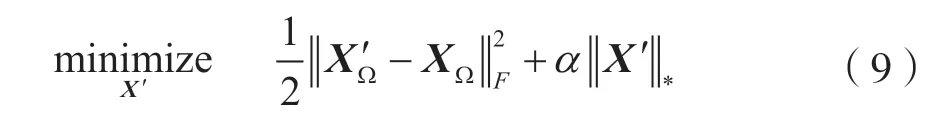
其中,||·||*表示矩阵的核范数,||·||F表示矩阵的Frobenius 范数,α是正则化系数。
对于一般阵列而言,如果有Mb阵元缺损,矩阵XΩ将出现Mb行的数据整行缺失(为零),此时不满足SIP 条件,不能直接通过求解凸优化问题(9)恢复缺失数据。因此,本文拟引入子空间约束构造新的凸优化问题,从而解决数据矩阵整行缺失时的数据恢复问题。
3 引入子空间约束的阵元缺损的数据恢复算法
3.1 子空间加权的矩阵填充方法
通过利用矩阵X子空间的先验信息,文献[9]提出了一种子空间加权MC 方法。
对矩阵X进行奇异值分解,得到:

其中QUK,ω和QVK,ω分别表示子空间UK和VK的投影矩阵的加权矩阵,权值ω∈(0,1]。
利用QUK,ω和QVK,ω,基本的MC 问题(8)可转换为子空间加权MC 问题:

比较式(8)和式(10)可知,当ω=1 时,式(14)退化为式(8),可见子空间加权MC 方法是基本MC 方法的推广。
与基本的MC 问题类似,子空间加权MC 方法可转化为凸优化问题:
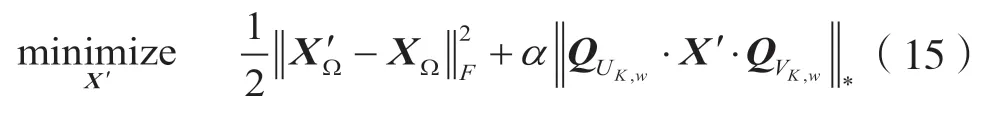
3.2 子空间的估计
由3.1 节可知,子空间加权的MC 方法需要子空间UK和VK的先验信息。但是,在实际运用时,完整数据矩阵X是未知的,已知的数据矩阵为XΩ,因此必须要利用XΩ对子空间UK和VK进行估计。文献[9]中的策略是通过对矩阵XΩ进行SVD 分解来获得子空间UK和VK的估计。

3.3 近端梯度下降法求优化问题(15)
仔细观察式(15)的优化问题可知,该凸优化问题的目标函数是两个凸函数之和,其中一个凸函数可微,而另一个凸函数不可微。根据优化理论,这类凸优化问题可用近端梯度下降法(Proximal Gradient Descent)进行求解[10]。
令Y=QUK,w·X´·QVK,w,则式(15)的优化问题可表示为:

令:
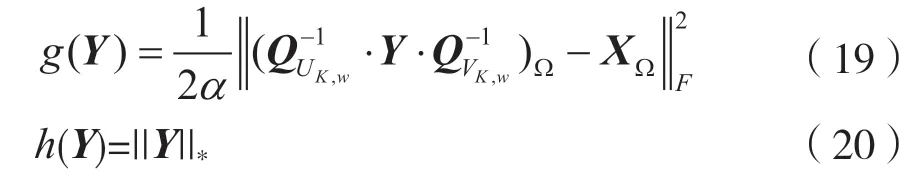
显然,优化目标函数f(Y)=g(Y)+h(Y)、g(Y)可微,h(Y)不可微。根据近端梯度下降算法的原理,式(18)的优化问题分两步进行。
首先,利用可微函数g(Y)的梯度对Y进行迭代更新,即:

其中w>0 为步长,Δg(Y)表示g(Y)的梯度,表达式为:


从而获得优化问题(15)的解X´。
值得指出的是,式(19)和式(21)中的步长参数w 有两种方法确定,即采用固定步长或使用线性搜索方法来确定[11]。
3.4 整行数据缺失的数据恢复算法
由于阵列的部分阵元缺损导致阵列接收数据矩阵的一些行全为0(整行缺失),此时不能用常规的矩阵填充方法恢复缺失的数据。通过引入子空间约束,构造一个的矩阵填充问题,可以有效恢复缺失的数据。基于讨论和分析,整行数据缺失的数据恢复算法总结如下。
输入:部分行整行缺失的数据矩阵XΩ,整行缺失的元素位置集合Ω,阵列的几何结构;
初始化:

4 仿真实验与分析
4.1 仿真条件和评价性能的指标
仿真实验中,天线阵列设置为二维均匀圆阵,阵元数M=8,圆阵半径等于波长;阵元缺损的数目Mb=4 且是随机缺损,即每次实验随机关闭8 个阵元中的4 个阵元(缺损率为50%)。到达阵列的辐射源为两个不相关且等功率的窄带随机信号,其DOA 分别为(θ1,φ1)=(25°,50°)和(θ2,φ2)=(35°,40°);信噪比SNR 定义为
算法的参数设置:正则化参数α=10,子空间加权系数ω=0.01;近端算法中的步长参数w采用线搜索方法确定,初始值w0=1。
采用DOA 估计的平均误差和缺失数据恢复的相对误差来评价算法的性能。
DOA 估计的平均误差E1定义为:

恢复数据的相对误差E2定义为:

另外,仿真实验中快拍数L=500,随机的独立实验次数N=500 次。
4.2 DOA 估计的平均误差E1 与信噪比之间的关系
DOA 估计采用MUSIC 方法,在不同的信噪比条件下观察本文算法求出的DOA 估计的平均误差E1与信噪比SNR之间的关系,仿真曲线如图1 所示。
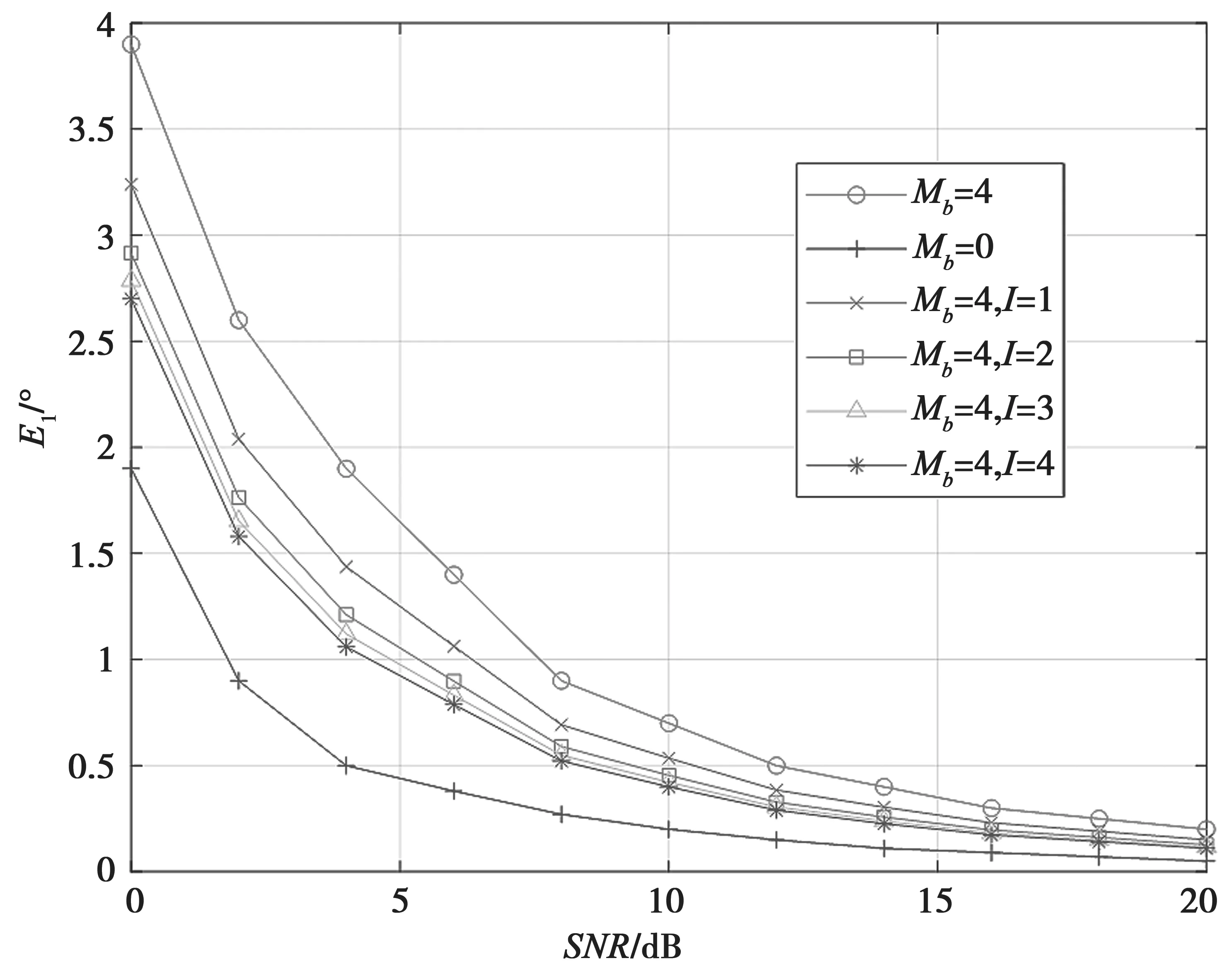
图1 E1 与SNR 的关系曲线
图1 中带“加”符号的曲线表示缺失4 个阵元(Mb=4)时,直接应用MUSIC 算法得到的估计角度的平均误差;带“圈”的曲线表示利用完整的8个阵元(无缺失阵元,Mb=0)和MUSIC 算法,得到的估计角度的平均误差;带“叉”和“菱形”符号的曲线都表示利用本文算法恢复缺失数据后,利用MUSIC 算法得到的估计角度的平均误差,带“叉”符号的曲线代表迭代次数I=1,带“菱形”符号的曲线代表迭代次数I=3。
由图1 可知,由于阵元缺损所导致的整行数据缺失,本文提出的算法能有效恢复缺失的数据,降低了DOA 估计的角度误差。另外,随着迭代次数的增加,角度估计的平均误差越小。在低信噪比时,缺失阵元带来的性能变化相对不大,而在较高的信噪比下进行矩阵填充后的性能改善明显。
4.3 恢复数据的相对误差E2 与信噪比的关系
在不同的信噪比条件下,利用本文算法恢复的缺失数据,其相对误差E1与SNR的关系曲线如图2 所示。

图2 E2 与SNR 的关系曲线
图2 中,带“圈”符号和“加”符号分别表示迭代次数为I=1 和I=3 时,利用本文算法恢复的缺失数据的相对误差。容易看出,当信噪比增加时,在不同迭代次数下,恢复数据的相对误差会逐渐减小。而在同样信噪比下,迭代次数增大,相对误差也会减少。
综合图1 和图2 的仿真结果可知,本文提出的数据恢复算法在低信噪比时,恢复数据的相对误差和DOA 估计的平均误差的性能改善较小,而在中、高信噪比时性能改善较大。这主要是由于各个阵元上的加性噪声是相互独立的,且噪声矩阵N不具有低秩性,同时噪声较大时子空间估计的误差也较大。本文算法主要是基于接收数据矩阵的低秩性和子空间约束设计的,所以在低信噪比时,性能改善要劣于高信噪比时的性能改善。
5 结语
本文提出了一种将子空间约束引入MC 理论的新方法,可以通过加权方式引入子空间约束,最终实现在一般阵列阵元出现缺损的情况下仍然能恢复接收数据矩阵。所提方法适用于一般阵列,可以解决二维角度估计问题,具有广泛的应用场景。

