海堤越浪量的人工神经网络模型算法
黄 建,董丽红
(大连理工大学土木建筑设计研究院有限公司,大连 116042)
海堤、防波堤、护岸是海岸防护工程中的常见结构。以往进行此类海岸工程建筑物设计时,常采用波浪最大爬高控制的设计方法,往往导致堤顶高程较高,在某些清况下是不经济的,因此逐渐被以允许越浪量为准则的设计方法所取代。越浪量是影响海堤结构形式的重要因素,它决定着堤顶高程、消浪肩台高程和宽度、边坡坡度等多个设计参数,并最终影响工程造价。同时也关系到堤后方掩护建筑物的安全、顶面行车行人安全、掩护水域船舶泊稳等情况。因此如何准确预测结构的越浪量是工程上十分关心的问题。
20世纪80年代,日本的合田良实进行了不规则波越浪量的试验研究,Owen[1]根据大量物理模型试验资料推导出不考虑坡面粗糙度防波堤的越浪量计算公式。Van der Meer[2]对斜坡堤越浪量进行了大量的研究工作,提出了单坡和复坡斜坡堤平均越浪量及最大越浪量计算公式,该公式被荷兰防洪设施技术咨询委员会(TAW)所采纳使用。各国规范也规定了不同的越浪量计算公式[3],国内较常用的公式是《港口与航道水文规范》[4]公式,而国外较常用的是Owen公式,Van der Meer公式、EurOtop公式[5]。在实验研究方面,国内王红[6]通过不规则波物理模型试验,提出了单坡堤上平均越浪量计算方法;李晓亮[7]通过整体物理模型试验,提出了斜向波和多向波在斜坡堤上的平均越浪量计算公式。周雅等[8]通过物理模型试验,研究了不同波要素和断面尺度对斜坡堤越浪量的影响,比较了随机、规则两种扭王字块体摆放型式的消浪效果。以上所涉及公式大都针对简单断面形式,且各公式均有一定的适用范围,不能完全满足海岸工程中各种复杂形式海堤越浪量的计算需要。
1 平均越浪量经验公式
1.1 中国《港口与航道水文规范》
中国《港口与航道水文规范》中明确规定,对于斜坡堤无胸墙情况下的越浪量可依据式(1)进行计算,对于有胸墙时堤顶越浪量按式(2)计算。计算方法是南京水利科学研究院通过模型试验提出的[2],与大连理工大学方法计算结果较为接近。
(1)
式中:Q为单位时间单位底宽的越浪量,m3/(m·s);A为经验系数;KA为护面结构影响系数;H1/3为有效波高,m;Tp为谱峰周期,s;Hc为堤顶在静水面以上的高度,m;m为斜坡坡度系数,斜坡坡度为1:m;d为建筑物前水深,m;g为重力加速度,m/s2。
(2)

1.2 EurOtop公式
欧洲较常用的EurOtop公式,该公式出自规范EurOtop Mannual(2018 II),其斜坡堤平均越浪量计算公式基于大量试验数据和实际工程资料分析得到,根据使用者目的不同分为概率设计与确定性设计两种计算方法。
(1)概率设计计算公式。
1)当ξm-1,0<5,破碎波和未破碎波越浪量计算公式分别如下
(3)
(4)
2)当ξm-1,0>7
(5)
(2)确定性设计(安全评估)计算公式。
1)当ξm-1,0<5,破碎波和未破碎波越浪量计算公式分别如下
(6)
(7)
2)当ξm-1,0>7
(8)
而对于5≤ξm-1,0≤7的情况,可采用线性内插法计算求得。

2 神经网络模型简介
在过去的十几年中,人工神经网络模型法被广泛应用于海岸工程中[9]。人工神经网络(Artificial Neural Networks)由大量神经元连接而成,是对人脑思维方式抽象和模拟的复杂网络系统。具有强大的学习能力、容错性与自适应性。它具有强大的映射能力、高度的不确定性和非线性特性,可以实现复杂的因果关系分析,在很多领域得到了广泛的应用[10]。国内陈茂聪[11]利用人工神经网络模型对溢洪道流量系数进行了分析。霍俊波等[12]构建了基于径向基(RBF)神经网络算法的桥墩局部冲刷深度预测模型,并分析了模型预测结果的误差分布。张娜[13]运用神经网络对水位流量关系率定。以上这些均体现了神经网络模型在水利学方面的应用。但在海堤越浪量研究方面,国内很少有文献提及这种方法。
早前存在两个神经网络模型,一个是CLASH项目中由荷兰代尔夫特水力学所发明的神经网络,它是一个运行软件,可以从EurOtop规范的官网上或者CLASH官网上下载使用。另一个神经网络也是基于CLASH项目,是Gent University(VERHAEGHE,2005)的博士论文的一部分。它是基于Matlab开发的,仅支持在Matlab环境下运行,导致工程人员很少使用。较早版本的ANN模型可见于Van Gent等[14]的相关研究成果。本文所述的人工神经网络是对原EurOtop预测工具的改进,可以直接在网页上执行文件。它基于更大数据集,也能更好地预测低越浪量值。EurOtop ANN模型数据库基于全世界多个研究所、实验室及欧盟资助的CLASH、DELOS、THESEUS项目,包含近18 000组物理模型试验数据。经过多年研究与发展,模型在以下方面得到了改进:通过增加模型数据库训练样本,提高了在高、低越浪率情况下q值的预测精度[15];通过对神经网络结构和训练特征的分析,在不降低平均精度的前提下提高神经网络的泛化能力[16];除使用置信区间外,引入一种创新方法来粗略评估预测的可靠性。
与应用经验公式计算越浪量不同,神经网络模型建模时包含大量控制参数,从而能够表示复杂结构几何形状和不同的波浪条件。与数值模拟试验不同的是,ANN模型瞬间完成预测,准确性及时效性都较强。ANN框架结构如图1所示。模型以层的形式组织,在每一层中都有一个或多个称为“神经元”的处理单元。第一层是输入层,包含15个神经元;最后一层是输出层,神经元数目等于要预测输出的参数数目。输入和输出层之间是隐藏层。每一层中的每个神经元通过连接从前一层接收信息,执行一系列标准操作并产生输出。作为神经网络校准的结果,每个连接都分配一个权重因子:通过在包含输入和输出参数的数据库上训练神经网络来实现,这是模型学习的过程。神经元的输入由前一层的输出加权和组成,神经元的输出由线性激活函数生成,输出神经元生成神经网络的最终预测值。

图1 ANN框架图Fig.1 ANN frame diagram
3 算例对比
利用EurOtop、 ANN模型,通过具体实例计算越浪量,并与传统公式计算结果进行比较,验证该神经网络模型的可靠性。采用防波堤断面如图2所示,堤顶设挡浪墙,挡浪墙外侧水平铺设扭王字块,下方为坡度1:1.5的6.5 t 扭王字块随机摆放护面,在平均水位附近设置水平消浪肩台,宽度为可规则摆放3排6.5 t 扭王字块,肩台下方亦采用6.5 t扭王字块随机摆放护面,坡度为1:1.5,坡脚水平规则摆放2排15 t扭王字块,块体外侧为重300~500 kg护底块石。极端高水位3.56 m,设计高水位2.45 m;设计波高H13%=4.40 m,平均周期T=8.3 s。进行了不同挡浪墙顶高程、肩台宽度、边坡坡度组合的共10组工况。
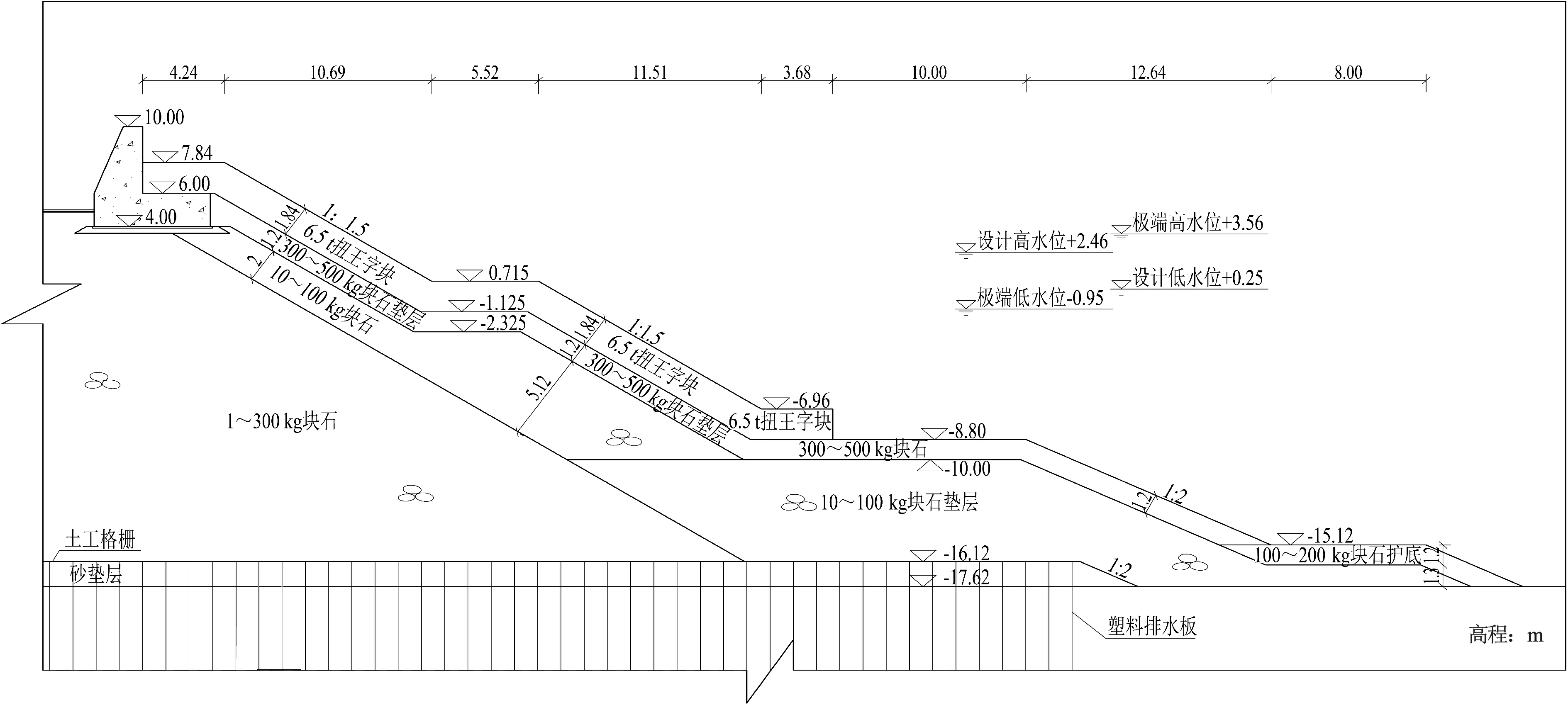
图2 试验断面(单位:m)Fig.2 Test section
利用ANN模型预测越浪量时,首先准备参数输入文件,新版的ANN模型需要15个输入参数,输入参数及其定义见表1及图3所示;将输入参数按指定格式输入模型后,经模型运算,即可得到平均越浪量q,也可根据需要计算输出波浪反射系数Kr及透射系数Kt。值得注意的是,模型输入参数所针对的Hm0,t为谱波高,Tm-1,0,t为谱周期,脚标t代表堤脚处的变量值。均是从能量谱的角度来描述波浪的,与常见的统计学波参数不同。深水情况下谱波高与有效波高相等(Hm0=Hs),浅水时二者有10%左右的差距。对于单峰波,谱峰周期与谱周期关系如下Tp/Tm-1,0=1.1。

表1 ANN模型输入参数 Tab.1 Input parameters of ANN
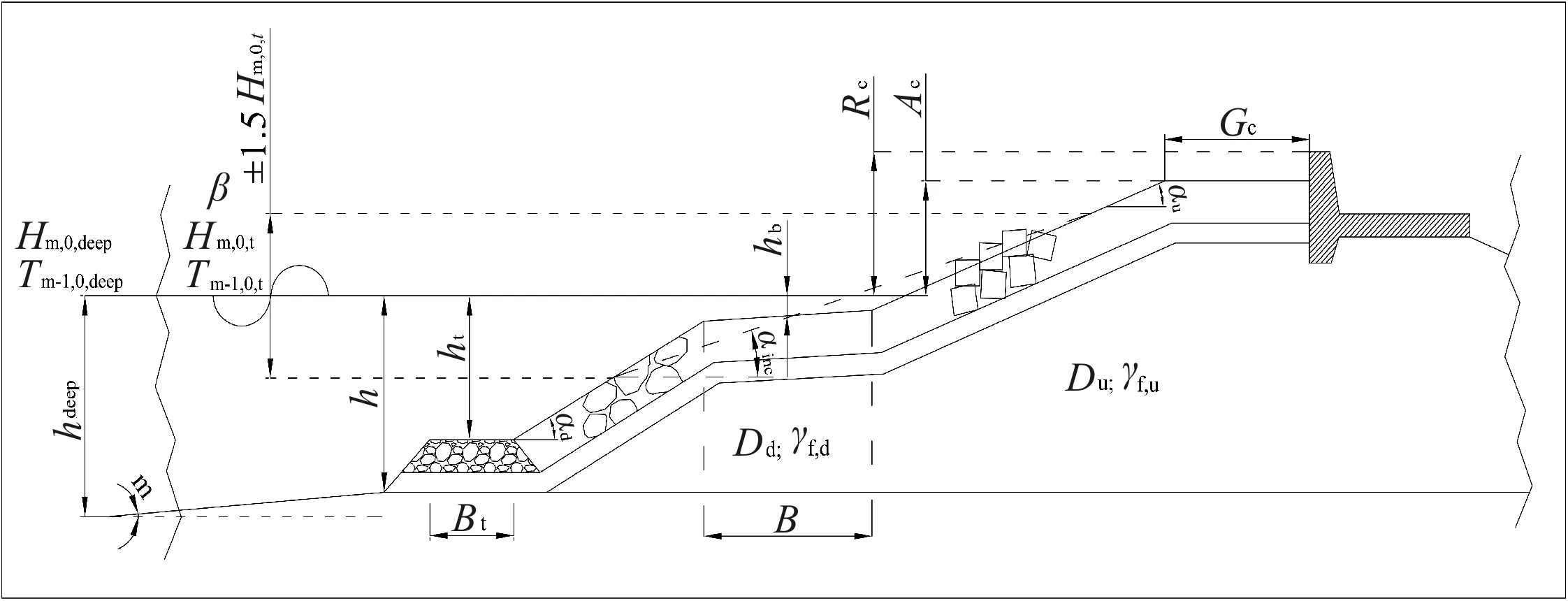
图3 基于CLASH的结构示意图Fig.3 Schematic diagram of structure based on CLASH
模型输出结果见表2,包含越浪量q的平均值、根据模型比尺效应修正的q的平均值、90%置信区间上下限值、E值。置信区间的使用,可以对于q值可能出现的范围有初步估计。E值表示模型预测的可靠性,越接近0表示预测的可靠性越高。使用者可根据需要选择q的平均值或某一限值,对结构的越浪量进行估计。该模型的优势在于,可以对护底、肩台、消浪平台、上下不同坡度、上下坡不同护面类型、混合堤等复杂断面进行计算,弥补了经验公式计算的不足。且计算快捷,适合在前期设计阶段,作为设计方案优化比选的辅助工具。

表2 ANN模型平均越浪量q预测值Tab.2 Prediction values of average overtopping q in ANN model m3/(m·s)
表3中工况1~9试验水位均是极端高水位,工况10为设计高水位。对比工况1和工况5结果,可知随着Gc增大,《港口与航道水文规范》和ANN模型预测的q值均降低了,这是符合常理的。对于工况3、4、7、9、10,ANN预测值与EurOtop公式计算结果接近,且均比《港口与航道水文规范》计算结果要小,可能的原因是《港口与航道水文规范》公式未能考虑消浪平台、护底结构等因素影响。对于工况4、10,ANN预测值与物模试验结果更为接近。值得指出的是,本次对比基于有限的实验数据,且仅为单个工程案例,很难说明各方法孰优孰劣。《港口与航道水文规范》是我国海岸工程领域多年研究和实践的总结,在绝大多数情况下结果是可靠的。ANN模型基于EurOtop开发,更适合基于欧标的工程设计中使用。
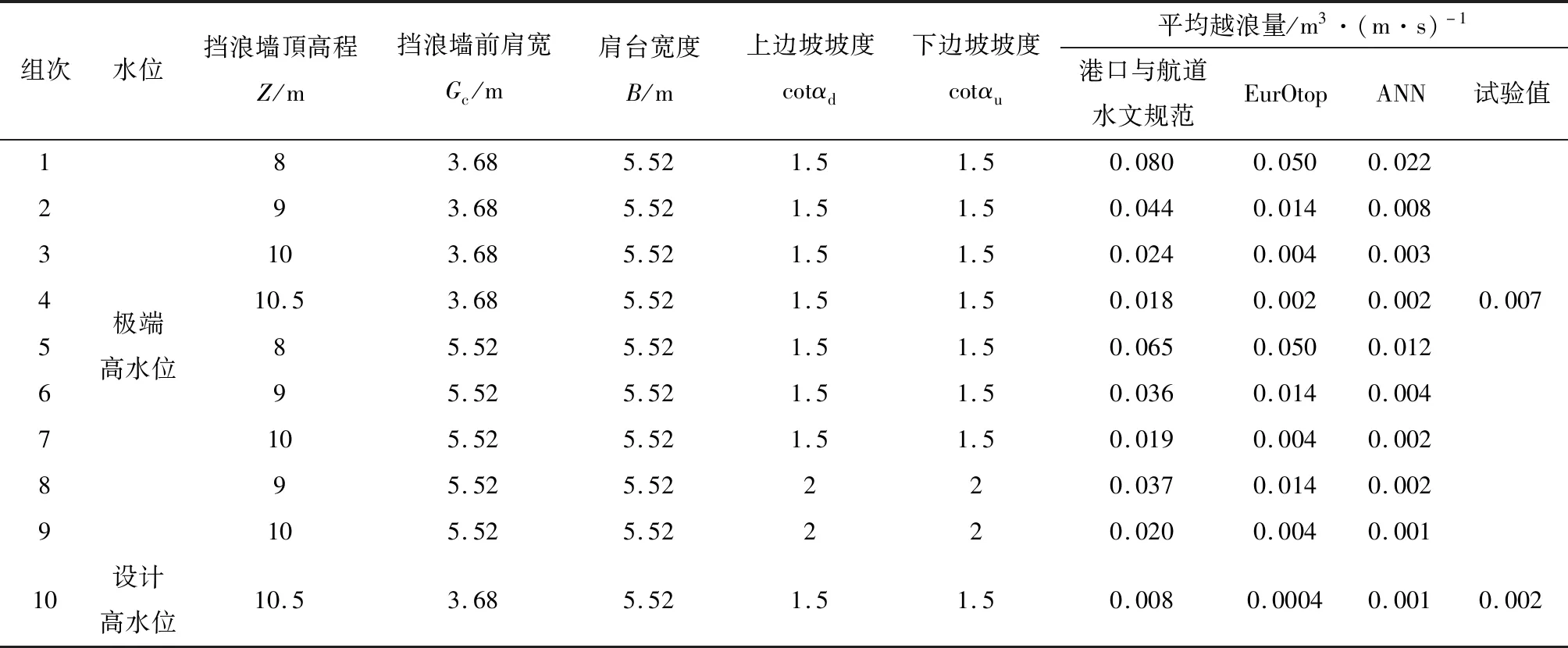
表3 不同方法下平均越浪量预测值比较表Tab.3 Comparison of prediction values of average overtopping under different methods
此外,还可以利用该神经网络模型考虑因素较多、计算简便快捷的特点,建立不同设计参数与平均越浪量的关系曲线图,从而判断越浪量对不同设计参数的敏感程度。如上述工程实例中,通过调节海堤堤顶在水面以上高度Rc、堤顶宽度Gc、肩台宽度B参数的大小,得到越浪量与各设计参数关系曲线如图4所示。从图4中各曲线斜率可知,对于该特定工程,越浪量最为敏感的设计参数为堤顶高度Rc,对顶宽Gc和肩台宽度B则较不敏感。因此在设计中可通过优化参数Rc,得到满足越浪量标准的设计断面形式。
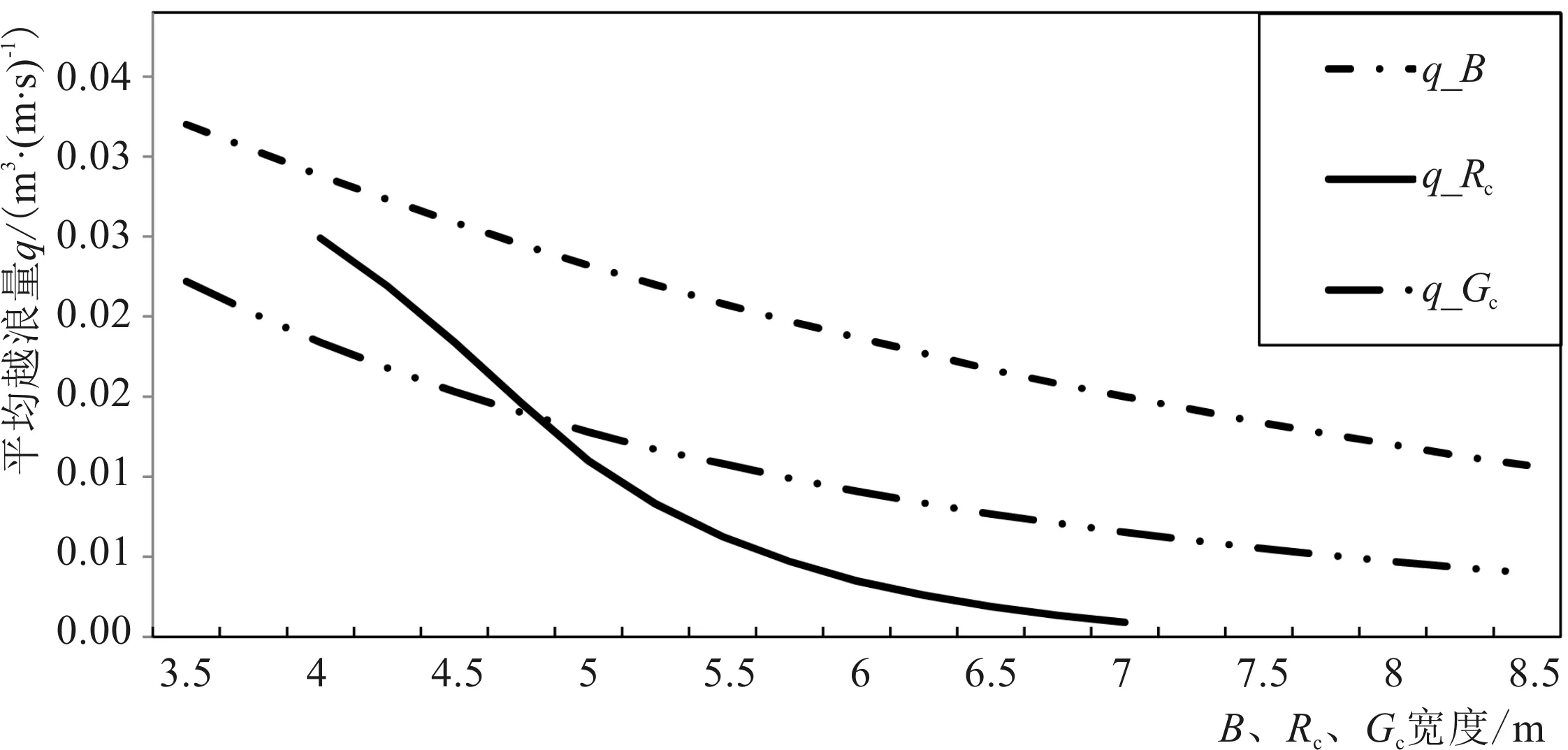
图4 平均越浪量q的敏感因素测试Fig.4 Sensitivity test of average overtopping q
4 结论
综上所述,本文对国外已经深入研究并广泛应用于工程领域的人工神经网络模型在斜坡堤越浪量方面的应用现状及使用方法进行了介绍,并结合实例对模型预测精度进行了评述。随着对模型研究的不断深入以及在数据库扩展方面的发展,相信在不远的将来,国内学者将会针对这一新的方法进行更为深入研究,收集整理国内诸多斜坡堤越浪量物模试验成果,对EurOtop ANN开放的数据库进行扩充,开发新的神经网络模型算法,逐步提升人工网络模型算法在中国海岸工程领域的应用研究水平。

