基于HMM的煤矿底板突水短时预测模型

杨 坤，陈伯辉,,施式亮

(1.福州大学环境与资源学院,福建 福州 350108；2.湖南科技大学资源环境与安全工程学院，湖南 湘潭 411201)

煤层底板水害作为常见的煤矿水害类型之一，由于其危险性较大、突发性较强等特性，一直以来是我国煤矿安全研究的重点问题之一。自20世纪60年代至今，我国开展了大量有关煤矿安全方面的研究，并取得了重要成果。近年来，在煤矿底板突水预测方面，常见的方法包括突水系数法、五图双系数法、脆弱性指数法、GIS拟合模拟法、突变级数法等[1-8]。 其中，突水系数法简单易用，但判断精度不高；五图双系数法较为全面，但工作量较大，现场实施较为困难；脆弱性指数法和GIS拟合模拟法较为全面，但存在评测因素选取客观性不足的问题；突变级数法评测准确度同样受限于评判指标及其权重的选取。

基于已有研究，本文拟在突水系数法的基础上，引入隐马尔科夫模型(HMM)作为煤矿底板突水过程分析的基本原理，并结合Ts-q法[9]，从单位涌水量q、相对安全状态下最大突水系数Tmax和实际突水系数Ts3个指标构建以条件概率为依托的预测模型，从概率统计的角度出发来规避评测因素选取客观性不足等问题，使建立的预测模型具有数据获取难度低、使用简单、易于推广等特性。

1 突水系数阈值与单位涌水量

1. 1 突水系数阈值分布

突水系数阈值预测模型在突水系数阈值的设定方面参考了Ts-q法，并在其基础上做了相关的改进。如图1所示，常见的Ts-q法通过建立平面直角二维坐标系，确定横、纵坐标分别为单位涌水量q和突水系数Ts的状态点分布，当突水系数的实际状态点处于标定的安全面积内则判定为安全[9]。因此，构成相对安全区域的边界可视为突水系数阈值即最大突水系数Tmax与单位涌水量q间的函数关系映射。

考虑到Ts-q法中相对安全边界呈现为折线段形式[10]归因于突水点分布的统计总结，故在此基础上探讨单位涌水量对应最大突水系数点的概率分布现象。若Ts-q法中相对安全边界两侧存在突水点随机分布且可做回归拟合，则最大突水系数Tmax满足与单位涌水量q间的线性或非线性关系且表现频次符合特定概率分布，见图2。根据突水系数对应的概率分布，进一步构建对应的隐马尔科夫链。

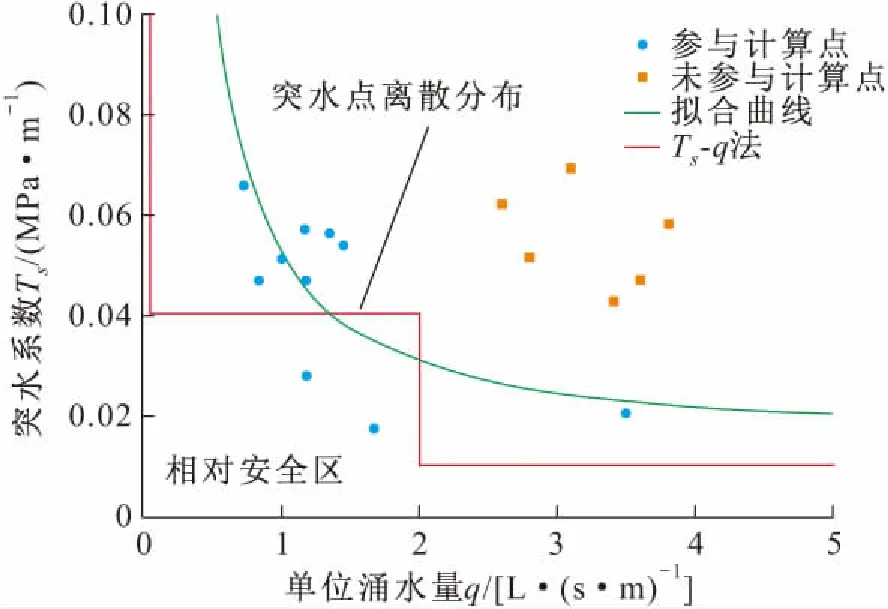
图2 突水系数概率分布示意图Fig.2 Schematic diagram of probability distribution of water inrush coefficient

1.2 最大突水系数与单位涌水量关系模型的构建

1.2.1 模型机制

在假定的隐马尔科夫模型中，单位涌水量作为观测量O，相对安全状态下的最大突水系数作为隐藏状态量X，构成隐马尔科夫链[11-14]，见图3。其中,X1,X2,…,XT分别指代不同观测时间段相对安全状态下的最大突水系数Tmax；O1,O2,…,OT分别指代不同观测时段的单位涌水量q。

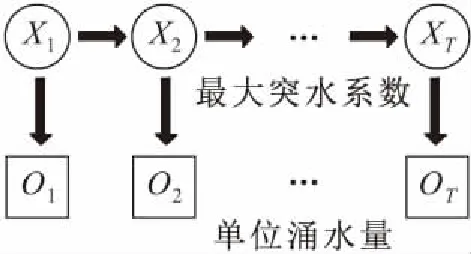
图3 最大突水系数与单位涌水量的隐马尔科夫模型机制Fig.3 Mechanism of hidden Markov model between water inrush coefficient and unit water inflow

1.2.2 模型要素构成

突水系数阈值即最大突水系数Tmax预测模型要素主要由单位涌水量观测区间个数n、状态转移矩阵A、表达矩阵B和初始状态概率向量π构成。

(1) 单位涌水量观测区间个数n。通过划分单位涌水量观测区间，确定观测集的元素个数及对应隐藏状态集的元素个数n，若初始模型的单位涌水量观测区间分为n段，则O1,O2,…,On为观测事件集合，即单位涌水量观测值的不同分布区间，X1,X2,…,Xn为隐藏状态集合，即不同单位涌水量分布区间对应的相对安全状态下的最大突水系数。

(2) 状态转移矩阵A。状态转移矩阵A为相对安全状态下最大突水系数Tmax的变化概率矩阵[11-15]，若模型预先设定的观测分段数为n，则该矩阵为n×n矩阵：

其中，aij表示第i个涌水量观测区间对应的相对安全状态下最大突水系数Tmaxi在下次数据采集时变化为第j个涌水量观测区间对应最大突水系数Tmaxj的概率，考虑到实际作业过程中隐藏状态变化的随机性和涌水量变化的不确定性，可设定对于任意i≤n且j≤n,aij取值为1/n。

(3) 表达矩阵B。表达矩阵B为任意单位涌水量区间qi(1≤i≤n)对应相对安全状态下最大突水系数Tmaxi的实际单位涌水量观测值表现为任意单位涌水量区间qj(1≤j≤n)的概率矩阵[11-15]。首先，根据所在矿区历史突水点的对应单位涌水量q、对应监测点突水系数Ts绘制Tmax为自变量的q值的分布图,并基于Ts-q中相对安全边界概念选取可作为临界参考值的突水点作为参与计算点，引入q值离散点概率分布概念，对q值离散点做回归拟合，见图4；然后，根据区间数n划分单位涌水量观测区间，基于拟合曲线确定各观测区间qi对应的突水系数最大值作为Tmaxi(1≤i≤n)，由于矿区突水点分布适用于简单非线性回归，故假设在自然条件下单位涌水量的区间分布概率符合以相对安全状态下最大突水系数Tmax为自变量的高斯分布，见图5;最后，通过概率分布计算，可得到表达矩阵B：

(1)

其中，Pij为第i个观测区间对应Tmaxi表现为第j个观测区间单位涌水量的概率;gi(x)为相对安全状态下最大突水系数为Tmaxi时单位涌水量q的概率分布函数;max(qj)和min(qj)分别为第j个观测区间的单位涌水量最大值和最小值，μi为第i个观测区间对应的单位涌水量均值；σ2表示离散程度，由单位涌水量q与相对安全状态下最大突水系数Tmax的关联性强弱决定，可根据断层构造及性质等条件进行判别，在实际条件不明的状态下，可根据参与计算突水点最大突水系数-单位涌水量回归曲线方差确定。

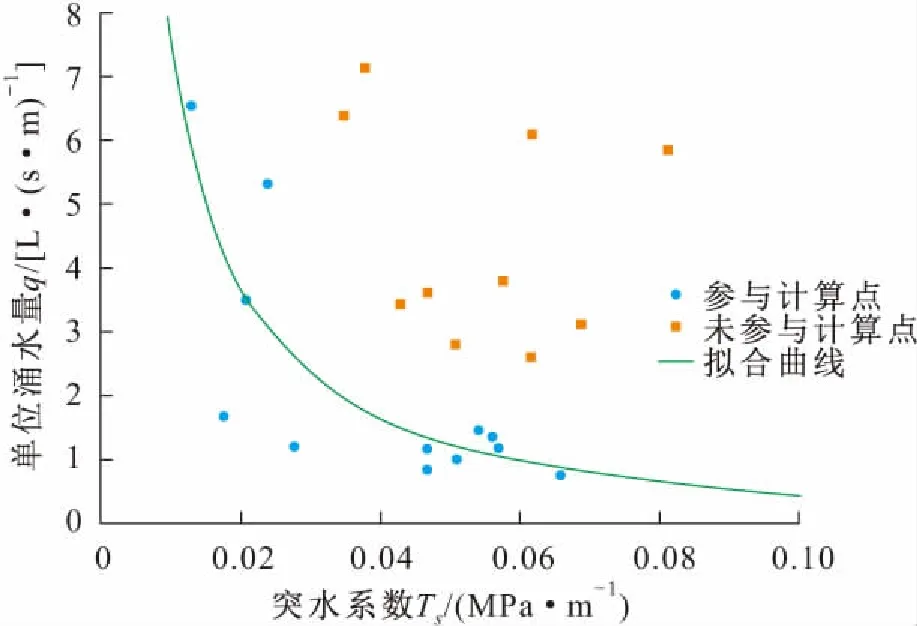
图4 矿区突水点单位涌水量分布示例图Fig.4 Example diagram of unit water inflow distribution of water inrush point in mining area

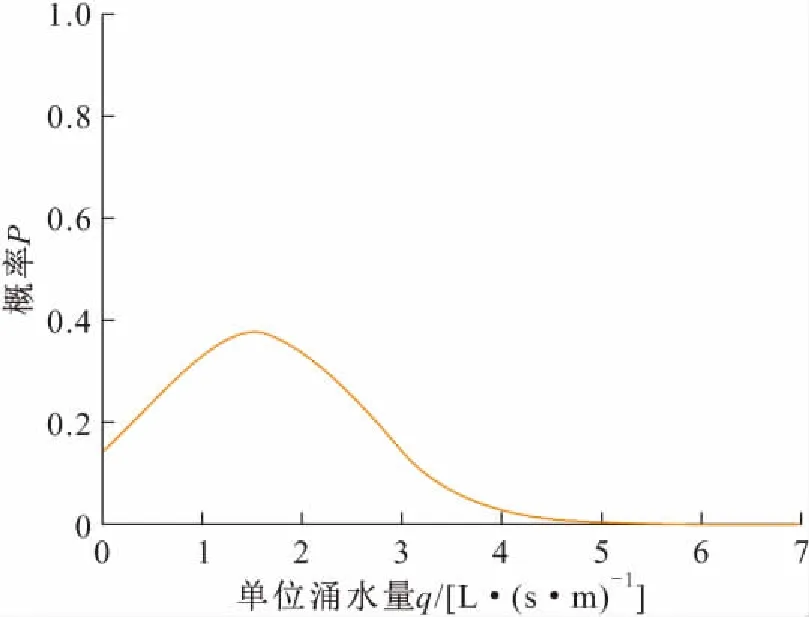
图5 突水系数对应单位涌水量的概率分布示意图Fig.5 Probability distribution diagram of unit water inflow corresponding to water inrush coefficient

(4) 初始状态概率向量π。初始状态概率向量π=(π1,π2,…,πn)[11-15]，其中πi为初始时刻相对安全状态下最大突水系数Tmax为单位涌水量观测区间qi对应最大突水系数Tmaxi的概率，可通过统计矿区参与计算突水点分布，构造单位涌水量q为自变量的回归方程，计算当前单位涌水量对应最大突水系数的概率分布，进而求得：

(2)

其中，h(x)为q值确定情况下Tmax的概率分布函数;Tmaxi为观测区间qi对应Tmax回归曲线的Tmax最小值,当i=n时，Tmax(n+1)取区间qn中观测点突水系数最大值;k为修正系数,用于放大突水系数计算区间;μ为当前单位涌水量观测值所属区间对应回归曲线段的突水系数均值;σ2可根据参与计算突水点由单位涌水量-最大突水系数回归曲线方差确定。

1. 3 最大突水系数的预测

通过对突水系数阈值预测模型使用Viterbi算法，根据某时刻至今单位涌水量数据，推算可能性最大的对应相对安全状态下最大突水系数Tmax的变化过程[16-18]，从而计算得出当前Tmax的预测值。

过程如下：

(1) 输入变量：模型为λ=(A,B,π)，其中A为状态转移矩阵,B为表达矩阵,π为初始状态概率向量。单位涌水量观测序列(O1,O2,…,OT),其中O1,O2,…,OT分别指代不同观测时段的单位涌水量所属区间。

(2) 输出变量：相对安全状态下最大突水系数的变化序列(X1,X2,…,XT),其中X1,X2,…,XT指代与不同观测时间段相对应的最大突水系数预测值。

(3) 初始化:算法初始值计算公式为

δt(i)=πibi(O1) (i=1,2,…,n)

(3)

φt(i)=0 (i=1,2,…,n)

(4)

其中，δt(i)为在监测时间节点t时刻单位涌水量属于qi区间的最大突水系数Tmax最优路径经过结点的联合概率最大值;πi为初始时刻相对安全状态下最大突水系数Tmax为Tmaxi的概率；bi(O1)为Tmaxi表现为观测事件1即初始观测事件的概率；φt(i)为t时刻Tmax的最大概率变化。

(4) 递推计算：递推计算t=2,3,…,T时最优路径经过结点的联合概率以及计算该时刻对应隐藏状态:

(5)

(6)

其中，i=1,2,…,n,j=1,2,…,n为状态序号;aji为状态转移矩阵A中对应元素，表示由上一状态j转化为状态i的概率。

(5) 终止:通过T次计算，得出最终最大路径概率P*及Tmax最终变化值XT为

(7)

(8)

(6) 最优路径回溯:对于t=T-1,T-2,…,1有:

Xt=φt+1(Xt+1)

(9)

求得最优路径为

X*=(X1,X2,…,XT)

(10)

其中，XT即为当前相对安全状态下最大突水系数的预测值。

2 突水系数与单位涌水量

2.1 突水系数与单位涌水量的关系模型构建

2.1.1 模型机制

对于实际突水系数Ts的预测，同样采用隐马尔科夫链进行模型构建，实际突水系数预测模型中单位涌水量作为观测量，而实际突水系数则作为隐藏状态量，构成隐马尔科夫链。

2.1.2 模型要素构成

实际突水系数预测模型要素主要由单位涌水量观测区间个数m、状态转移矩阵A、表达矩阵B和初始状态概率向量π构成。但与相对安全状态下最大突水系数预测模型相比，实际突水系数预测模型的初始参数及使用方法存在差异。由于实际突水系数与单位涌水量之间存在一定关联但具有不确定性，故实际突水系数预测模型需要适量初始测算数据作为建模依据，包括一定时段各单位涌水量区间qi对应的实际突水系数监测数据即底板水压和隔水层厚度。

另外，在数据选用方面，该模型无须划分有效点作为参与计算点；在区间划分上，考虑到该模型监测数据量较突水点数据量大，可在适当范围内增大观测区间数m以提高预测精度；在参数构造方法选择方面，考虑到该模型实际突水系数测算数据获取有限，难以形成大量训练样本来支撑常见监督学习算法，故优先采用概率分布算法，若实际突水系数监测数据获取难度较大或数据可靠性低，则采用Baum-Welch算法[18]基于单位涌水量观测值开展实际突水系数的计算。

(1) 状态转移矩阵A:对于状态转移矩阵A，根据模型预先设定的观测区间分段个数m来确定该矩阵结构：

其中，aij表示第i个涌水量观测区间对应的实际突水系数Tsi在下次数据采集时变化为第j个涌水量观测区间对应的实际突水系数Tsj的概率,考虑到实际作业中含水层中的静水压力与隔水层厚度变化的随机性，可初步设定对于任意i≤m且j≤m,aij取值为1/m。若缺少实际突水系数Ts观测数据，则采用Baum-Welch算法[18]基于单位涌水量观测值开展模型参数的计算。

(2) 表达矩阵B:对于表达矩阵B，其矩阵结构为

若实际突水系数Ts观测数据充足且可靠，则根据观测点Ts值计算其回归曲线，划分单位涌水量区间qi及对应突水系数区间Tsi(1≤i≤m)，则有：

(11)

其中，Pij为第i观测区间对应Tsi表现为第j观测区间单位涌水量的概率；fi(x)为实际突水系数Ts对应Tsi时单位涌水量q的概率分布函数;max(qj)和min(qj)分别为第j观测区间的单位涌水量最大值和最小值;μi为第i观测区间对应单位涌水量均值;σ2表示离散程度，可根据观测点实际突水系数-单位涌水量回归曲线方差确定。

若缺少Ts观测数据或Ts对q值分布离散程度较大，可在初始样本数据积累之上，采用Baum-Welch算法[18]进行表达矩阵计算。故初步设定对于任意i≤m且j≤m,bij取值为1/m。

(3) 初始状态概率向量π:对于初始状态概率向量π=(π1,π2,…,πm)，需在初始样本数据积累之上，构造以q为自变量、Ts为因变量的回归曲线，计算q值确定情况下Ts的概率分布，进而求得：

(12)

其中,l(x)为q值确定情况下Ts的概率分布函数;max(Tsi)和min(Tsi)分别为突水系数区间Tsi的最大值和最小值，当i=m时，Ts(m+1)为观测区间qm中观测点Ts的最大值；k为修正系数，用于放大突水系数计算区间；μ为当前q值所属区间对应Ts的平均值；σ2可根据观测点单位涌水量-实际突水系数回归曲线方差确定。

若观测工作较为复杂，无法准确测算Ts值，可初步设定πi取值为1/m，采用Baum-Welch算法[18]对模型初始参数进行修正。

2.1.3 模型初始参数修正

基于Baum-Welch算法[18]的模型参数修正计算过程如下：

(1) 输入变量：单位涌水量观测序列V(O1,O2,…,OT)。

(2) 输出变量：隐马尔可夫模型参数λ=(A,B,π)。

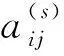
λ(0)=(A(0),B(0),π(0))

(13)

(4) 递推计算： 递推，对于s=1,2,3,…,则有：

(14)

(15)

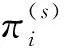
(16)

其中,T为观测序列长度;ξt(i,j)为给定模型λ和观测序列V情况下，在时刻t表现为qi且在时刻t+1表现为qj的概率;γt(i)为给定模型λ和观测序列O情况下，涌水量区间qi与突水系数区间Tsi相匹配的概率;ξt(i,j)和γt(i)由λ(s-1)=(A(s-1),B(s-1),π(s-1))和观测序列V求出;Ot=qi表示t时刻观测值Ot属于涌水量区间qi。

(5) 终止：经过多次迭代，λ(s)=(A(s),B(s),π(s)),即λ的极大似然估计。

2. 2 实际突水系数的预测

通过多次测算不同单位涌水量区间对应的实际突水系数，形成预测模型的初始样本数据，进而计算得到状态转移矩阵A、表达矩阵B和初始状态概率向量π，采用Viterbi算法[16-18]，根据某时刻至今单位涌水量数据，推算实际突水系数的变化过程，从而计算得出当前实际突水系数的预测值。

3 基于单位涌水量的煤矿底板突水短时预测实例应用与分析

将上述建立的突水系数阈值预测模型和实际突水系数预测模型进行功能组合，则构成基于单位涌水量的煤矿底板突水短时预测模型。通过对比该复合预测模型计算得出的相对安全状态下最大突水系数预测值与实际突水系数预测值，若当前实际突水系数预测值大于相对安全状态下最大突水系数预测值，则可初步判定当前状态下发生煤矿底板突水的可能性较大。实际应用中，该预测模型适用于由于部分客观因素导致难以开展突水系数定时测算的工作情况。

本文以焦作矿区为案例，通过对韩王煤矿、焦西煤矿、王封煤矿、李封煤矿、演马庄煤矿、九里山煤矿和中马村煤矿7个煤矿多个突水点采用基于单位涌水量的煤矿底板突水短时预测模型进行案例计算与分析[19]，以验证该预测模型的可行性。

根据焦作矿区突水点分布[9,19]，选取用于构建相对安全边界的参与计算突水点，绘制突水点分布图，并进行回归曲线拟合，见图6。

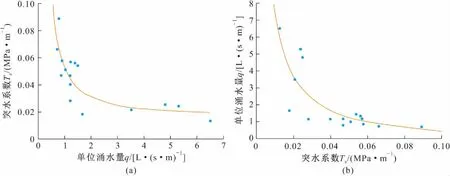
图6 焦作矿区突水点最大突水系数安全边界拟合曲线Fig.6 Fitting safety boundary of maximum water inrush coefficient of water inrush point in Jiaozuo Mining Area

然后，构造单位涌水量观测区间，代入拟合曲线计算对应单位涌水量区间的最大突水系数，其结果见表1。

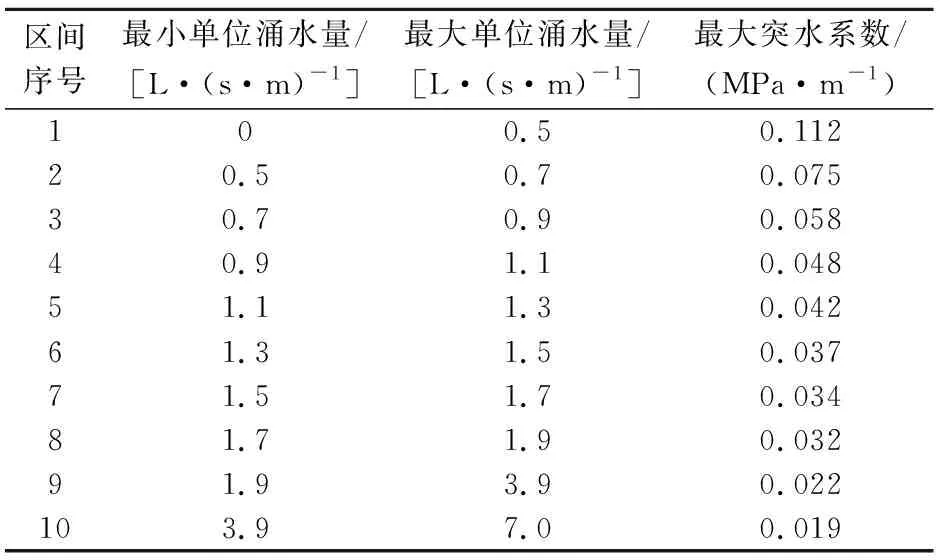
表1 观测区间及对应的最大突水系数

根据拟合曲线绘制各单位涌水量观测区间所含突水点突水系数均值对应的单位涌水量概率分布,计算得到表达矩阵B如下

设状态转移矩阵A为10×10矩阵，且矩阵A所有元素取值为0.1。

若取连续单位涌水量观测数据向量为：[1.4,1.4,1.4,1.4,1.4,1.4,1.4,1.4,1.4,1.4]，修正系数k设为50，则计算可得初始状态概率向量π=[0.03,0.12,0.14,0.12,0.09,0.07,0.05,0.19,0.06,0.12]。

使用Viterbi算法[16-18]计算得到相对安全状态下最大突水系数的最优路径为：[0.032,0.075,0.075,0.075,0.075,0.075,0.075,0.075,0.075,0.075]，即最大突水系数预测值为0.075 MPa/m。

若取连续单位涌水量观测数据向量为：[1.4,1.0,0.6,1.2,1.0,1.4,1.2,1.6,1.4,1.6]，则同理使用Viterbi算法[16-18]可计算得到相对安全状态下最大突水系数的最优路径为：[0.032,0.112,0.112,0.075,0.112,0.075,0.075,0.048,0.075,0.048]，即最大突水系数预测值为0.048 MPa/m。

本文基于单位涌水量的煤矿底板短时预测方法在相对安全状态下突水系数的预测最终结果与Ts-q法[9]整体较为相近，说明本文方法具有可行性。部分差异包括：①当前单位涌水量的前期连续观测值会对最终预测结果产生影响；②预测值随单位涌水量持续变动，在部分区间相较Ts-q法[9]偏高或偏低。

4 结论与建议

基于隐马尔科夫模型，结合条件概率理论，探索在监测数据有限条件下通过单位涌水量开展煤矿底板突水短时预测的新方法，得到主要结论如下：

(1) 基于Ts-q法，实现了突水系数阈值的概率分布设定，可用于构建突水系数预测模型。

(2) 基于隐马尔科夫链和概率统计算法，构造以单位涌水量为观测数据的最大突水系数和实际突水系数预测模型，实现了煤矿底板突水的短时预测。

(3) 在条件允许的情况下，实际突水系数采用现场测算的方法可提升模型的预测精度。此外，结合相关实际数据进行反馈分析，本模型在相关参数的标定算法上仍可做进一步的改善。