叶落知秋，见微知著

何江英

摘要：在低段的数学教学中，学生经常会出现一些浅显易见的错误，如果教师视而不见，归结为粗心大意，那么就会错过最好的教学时机。作为教师应该对于学生常出现的错误，寻求其背后的原因。笔者从思维的自我中心性、不可逆性、不守恒性、不集中性四方面进行了思考分析，并提出了几点在教学上的建议，以促进学生的发展。

关键词：数学错误;思维;认知发展

中图分类号：G623.5     文献标识码：B    文章编号：1672-1578（2020）34-0295-02

1.引发思考

教学片段：《20以内数的认识》

师：同学们不仅会顺着数，倒着也会数数，那老师来考考大家：18的前面是几？

生：18的前面是19。

师：前面的数比18大还是比18小？

生：小。

师：那么，18前面应该是几？

生：18前面是17。

……

学生这样的错误回答，在低段的教学中是常见的，甚至有些类似错误在高段也是屡见不鲜。上过这一课的老师们都明白，大部分教师处理此类错误的方法就是以上教学片断中教师的处理方式。可是，在作业中，学生还是照错不误，这又是为何？于是，引起了笔者深深的思考。

2.寻找真相

2.1 思维的不可逆性。

分析低段学生的认知状况，主要处于前运算阶段的后期或者具体运算阶段的前期。在此阶段中，学生能够借助表象进行思维运动，但是思维却是不可逆的，可逆性改变人的思维方向，使之回到起点，而前运算阶段的儿童不能这样思维，通俗的说就是缺少逆向思维能力;所以说，学生对事物的理解是是单薄的，还不太会从多方向理解知识，分析知识。

正如前面的教学片段中，教师虽然是在教学了数的顺序后提出这样的一个问题，但是部分学生在面对实际问题时，并没有把顺着数数和倒着数数区分开来，数的时候也如小和尚念经一样有口无心，甚至模仿其他同学。理解数的先后顺序时，他并没有形成逆向思维，因此无法主动得到正确的答案。

由思维的不可逆性造成的错误，在低段数学的运算当中屡见不鲜。如提问2+（ ）=6，（ ）-4=5，我们经常会得到这样的错误答案：2+（8）=6，（1）-4=5。面对这样的情况，老师们经常觉得不可思议，难道学生不会试着想一想：2+8会等于6吗？1-4会等于5吗？没错，这各阶段的许多孩子就是不会进行这样的思维过程，他们看到“+”，想到的是把两个数相加，看到“-”，想到的是把两个数相减，且一般默认用大的数去减小的数。

当然，大部分学生不会发生这种错误，那么他们应该进入了具体运算阶段，可逆性逐步形成，并借助传递性，能够按照事物的某种性质如大小、出现的时间、长短等进行顺序的排列。

2.2 思维的自我中心性。

自我中心是指兒童在思考问题时总是以自己的角度为出发点，这并不是说前运算阶段的儿童很自私，而是指他们以为别人看到的世界与他们看到的是一样的。这个阶段的孩子在考虑问题时总是站在自己经验的中心，只有参照他自己才能够理解其他事物，以模仿性思维为主。体现在以上教学片段就是，有些学生理解的“数下去”就是“往前面数”，就像我们走路是往前走的，他们把自己看作了问题的中心，只是依照惯性思维从小到大来数，那么，自然而然18的前面就是19了。这些问题都源于学生的认识发展过程。

2.3 思维的不集中性。

出现教学片段中的问题，还有一些同学给出的原因可能是没仔细看。很多时候，我们总是把学生在学习上的尤其是作业上的错误，归结为“粗心”，在计算中，数字的顺序经常会看错，运算符号经常会搞错，尤其前面是乘法算式，后面出现一题是除法算式时，学生很容易把最后一题的除法算式当做乘法算式来计算。真的只是因为“粗心”吗？

数学的学习囊括了极其复杂的心理活动，它不是一个单一平面化的过程，意志、动机、态度、个性往往起非常重要的作用。数学推算过程注重强大的逻辑构架和清晰理性思维，往往需要学生对题目“咬定青山不放松”的坚定意志;符号与符号的碰撞之抽象，数字与数字的交融之复杂，需要学生自信心与动机兴趣的正向推力;小学数学问题的解决十分注重群体的竞争、合作意识，于是保持诚恳的态度至关重要。

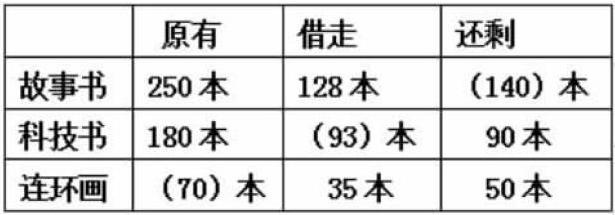
下表是学生一次作业，括号里的是学生的错误答案：

求原有、借走、还剩的这样的表格，对于学生并不陌生。为什么会有这样的错误呢？一方面是由于学生思维不集中，受思维定势影响，因为平时的练习都是竖着看的，而本题是横看的，部分学生仍把它当作是平时练习的方式，没有看自信，凭感觉就填写了答案。另一方面，由于学生不会看表格，对题意还没有十分的理解，他们看到数据就进行加加减减，对于数学概念的本质还是十分模糊的，没有自己的理解。所以，我们不能笼统把这样的错误归结为“粗心”，而是要寻找这所谓“粗心”背后的真相。

3.提出对策

课程标准指出：教师通过学习小结对学生的学习情况进行评价，可以反思自己的不足以及需要改进的地方，分析反思教学过程中影响学生学习能力发展和素质提高的原因，寻求改善教学的对策。

3.1 尊重学生的认知规律。

低年级学生学生思维特点主要以形象思维占优势，抽象思维相对较弱。这就需要首先在学生头脑中建立正确而丰富的表象，让学生试着自己去感知、理解、探索、发展，从而建立新的认知结构，让学生真正理解知识的内涵和概念的本质属性。如在学习加法时，我们要结合具体的情境，有意识地引导学生，使其了解加法的本质。但在现实情况中，很多老师认为多重复几遍，学生自然会记住，便采取简单地说教、乏味地练习，明显忽略了数学思维的培养。这样枯燥无味的、不尊重学生认知发展规律的教学只会让学生丧失学习兴趣，结果会适得其反。

3.2 丰富学生的生活体验。

课标中指出：“学生能够认识到数学存在于现实中，并被广泛应用于现实世界，才能切实体会到数学的应用价值。”数学本源于生活，教师教学要抓住与学生生活经验的最佳联结点，并架起桥梁，变传统的“书本中教数学”为引领学生在“生活情景中学数学”。我们要鼓励学生在生活中发现数学，感受数学，提出数学问题，解决数学问题，增强学生的数学意识，培养学生的数学兴趣和素养，提高学生的实践应用能力。

我们可以结合教材的教学内容设计数学实践活动、布置数学活动类家庭作业。比如超市购物、统计全校学生人数、测量自己的身高、外出旅游行程规划、经费核算等等。这样的学习活动一举多得，首先能更加具象地简化原本抽象的问题，便于学生的理解，其次能培养他们的自主创新能力和解决问题的能力，另外能埋下学习的记忆点，当学生在生活中碰到类似问题时能第一时间想起曾经做过的数学题，起到生活反作用于学习的效果。

3.3 关注学生的思维变化。

有人说，最好的课堂教学就是能关注到每一位学生的变化与发展。数学知识的教学，应注重学生对所学知识的理解。学生掌握数学知识，不能依赖死记硬背，而是应以理解为主。在理解和掌握知识的过程中，教师应通过课堂回答，课堂作业及课外练习训练等关注学生的学习细节，这些细节其实就是学生认识的思维过程。而在这过程出现的错误就是暴露出来的思维缺陷，应该引起教师的高度重视，并且对症下药。

学生学习数学是认知发展和认知建构的过程，在数学教师指导下，学生从已有的经验出发，主动获得对数学知识的理解与数学技能的掌握，并在思维能力、情感态度与价值观等多方面得到的进步和发展的过程。但是，低段的学生由于在生理和心理上的发展都不够成熟，所以对于知识的接受情况有强弱之分。如果教师忽视了这一事实，对于教学无疑是不利的，尤其后进生。教师应该再面向全体学生的同时，更加关注个体差异，掌握“事实真相”，促进学生全面、和谐、持续的发展。

参考文献：

[1] 义务教育课程标准（2011年版）[M].北京.北京师范大学出版社，2011.

[2] 栗玲.小学数学课程与教学论[M].北京：中国社会科学出版社，2010（09）.