空间序列低秩稀疏子空间聚类算法
由从哲 舒振球 范洪辉

摘 要:研究序列数据的子空间聚类问题,具体来说,给定从一组序列子空间中提取的数据,任务是将这些数据划分为不同的不相交组。基于表示的子空间聚类算法,如SSC和LRR算法,很好地解决了高维数据的聚类问题,但是,这类算法是针对一般数据集进行开发的,并没有考虑序列数据的特性,即相邻帧序列的样本具有一定的相似性。针对这一问题,提出了一种新的低秩稀疏空间子空间聚类方法(Low Rank and Sparse Spatial Subspace Clustering for Sequential Data,LRS3C)。該算法寻找序列数据矩阵的稀疏低秩表示,并根据序列数据的特性,在目标函数中引入一个惩罚项来加强近邻数据样本的相似性。提出的LRS3C算法充分利用空间序列数据的时空信息,提高了聚类的准确率。在人工数据集、视频序列数据集和人脸图像数据集上的实验表明:提出的方法LRS3C与传统子空间聚类算法相比具有较好的性能。
关键词:低秩表示;稀疏表示;子空间聚类;序列数据
中图分类号:TP391.4 文献标识码:A 文献标识码:2095-7394(2020)04-0078-08
序列数据特别是视频数据往往具有高维属性,利用传统聚类算法进行分析处理时,往往会遇到“维数灾难”的问题,于是研究人员提出了一系列基于表示的子空间聚类算法,如稀疏表示子空间聚类算法(SSC)和低秩表示算法(LRR),较好地解决了高维数据聚类的问题,从而得到了广泛的关注,并在众多领域得到成功的应用。但是,这类算法是针对一般数据集设计开发的,在许多实际场景中,数据通常具有顺序或有序的属性,例如视频、动画或其他类型的时间序列数据。然而,传统的方法假设数据点独立于多个子空间,而忽略了时间序列数据中的连续关系。如何充分利用空间序列数据这一特性提高聚类性能,是计算机视觉领域中一个重要但又具有挑战性的问题。假设这类数据在时间或空间的特定点以均匀的间隔采样,也就是时间序列数据。例如,作为时间函数的视频数据具有序列结构[1],在该结构中,可以假设大多数帧与其相邻帧相似,直到场景发生变化。
子空间聚类是解决高维数据聚类的有效方法之一,其基本假设是高维数据往往存在于低维子空间的并集中[2]。近年来,利用稀疏表示或低秩表示进行子空间聚类的研究受到广泛关注,并提出了一系列与之相关的新的子空间聚类算法,如稀疏子空间聚类(SSC)[3-4]、低秩表示(LRR)[2,5]及其变体LRSC[6]。这些算法的基本假设是:数据是自表达的,即其子空间中的每个数据点可以表示为来自同一子空间的数据点的线性组合。其中,基于表示矩阵核范数和L1范数最小化的LRR和SSC算法最受关注。这些算法主要是针对不连续的独立数据进行设计开发的,并没有特别考虑到处理时间序列数据的特殊性。此外,在时间序列数据的子空间聚类问题上,研究人员所做的工作并不是特别充分。
本文通过有效利用数据序列的性质,提出了一种低秩稀疏空间子空间聚类方法(LRS3C)。具体地说,是在子空间聚类算法模型中加入了一个惩罚项来加强近邻数据的相似性。采用交替方向乘子法(ADMM)[7]求解优化问题。为了验证提出的LRS3C方法的有效性,将其应用于视频场景分割和人脸聚类的实际问题中。实验结果表明,该方法具有良好的性能。
1 相关工作
目前,大多数子空间聚类算法没有充分考虑时间序列数据的序列性,也就是说,数据样本要么是空间域中的邻居,要么是时间域中的邻居。视频是时间序列数据的一个常见例子,每个帧可以被矢量化为单个列[Xi],并与相邻帧并排放置以形成数据矩阵[X]。这种顺序应反映在矩阵表示系数[Z]中,使得相邻域具有相似性,即[Zi=Zi+1]。在文献[8]中,Guo和Gao等人提出了空间子空间聚类(SpatSC)算法,其目标函数定义如下:
2 空间序列低秩稀疏子空间聚类算法
尽管SpatSC和OSC两种方法都是稀疏子空间聚类算法(SSC)的扩展,在序列数据方面取得了良好的效果,但仍有一些问题有待解决。SSC算法简化了学习任务,降低了模型复杂度,但是,SSC算法得到的系数矩阵Z往往过于稀疏,无法保证所构造的亲和图的连通性,这对后续谱聚类的处理有很大影响[10]。低秩表示(LRR)在捕获数据的全局结构方面要优于SSC,但是,LRR算法要求数据严格符合子空间独立的假设,这在实际应用中很难得到满足。因此,将这两种算法结合起来,从而为序列数据带来更好的聚类效果,特别是要恢复的底层表示矩阵同时是低秩和稀疏的情况。
在解决上述优化问题后,得到数据矩阵的低秩稀疏表示系数矩阵[Z]。下一步是使用表示系数矩阵构造亲和图,利用谱聚类算法对亲和图进行分割,得到最终聚类结果。本文建立一个加权图[Graph=ν,ε,W],其中[W=Z+ZT],然后将谱聚类[13]应用于亲和图,得到最终的聚类结果。
3 实验
在本节中,将评估LRS3C算法在三个数据集上的性能。首先,在一个合成数据集上对其进行测试;然后,在两个真实数据集上对其在视频场景分割和人脸聚类两个计算机视觉常见任务上的性能进行评估。
使用子空间聚类误差,
作为聚类算法性能的评价指标。
此外,还评估了所提出的LRS3C算法在加入额外噪声时的稳健性。在本文中,加入了均值和单位方差为零的高斯噪声,给出了该算法在不同噪声强度下的性能。使用峰值信噪比(PSNR)衡量噪声水平,其定义为:
其中,[I]是无噪声数据,[K]是有噪声近似值,[S]是[I]中的元素的最大可能值。PSNR值的降低表明噪声量的增加。由于式(17)的分母在无噪声情况下为0,将PSNR标记为“Max”。实验中给出的PSNR值为平均值。
3.1 人工数据集实验
本文创建了六个两两不相交的子空间,每个子空间的维数为4,并从每个子空间中抽取20个样本(样本维数为200)组成人工数据集。利用高斯噪声对数据集进行破坏,并评估LRS3C算法和对比算法OSC、SpatSC、LRR和SSC的聚类性能。每组实验重复了50次。
图1中给出了五个算法得到的表示系数矩阵Z的可视化比较,并在图2中给出了这些亲合矩阵的聚类精度的结果。实验中,加入了20%量级的高斯噪声,可以看到,所提出的LRS3C算法提供了更多的块状表示系数矩阵,这意味着它比其他方法包含更强的类内权值和更多的类内权值。可视化聚类结果也表明了LRS3C在实验中得到了最佳分割。另外两种矩阵算法OSC和SpatSC算法对序列数据也都得到了很好的分割,但是LRR和SSC算法则存在误分类的问题。
3.2 视频场景分割
评估LRS3C算法在视频场景分割方面的性能,其目的是从视频序列中分割单个场景。测试视频序列是从两个短动画中提取出来的。图3提供了要分割的序列的示例。序列的长度约为10秒(约300帧),每个序列由三个场景组成。视频1和视频2分别包括19和24个序列。要分割的场景可以包含对象的意义或变形,以及透视或相机视角的变换。人工采集场景变化(或关键帧)形成真实数据。
为了满足测试要求,将彩色视频转换成灰度视频序列,采样分辨率为129×96。序列中的每一帧被矢量化为[Xi∈R12 384],并与连续帧连接形成数据矩阵[X∈R12 384×300]。
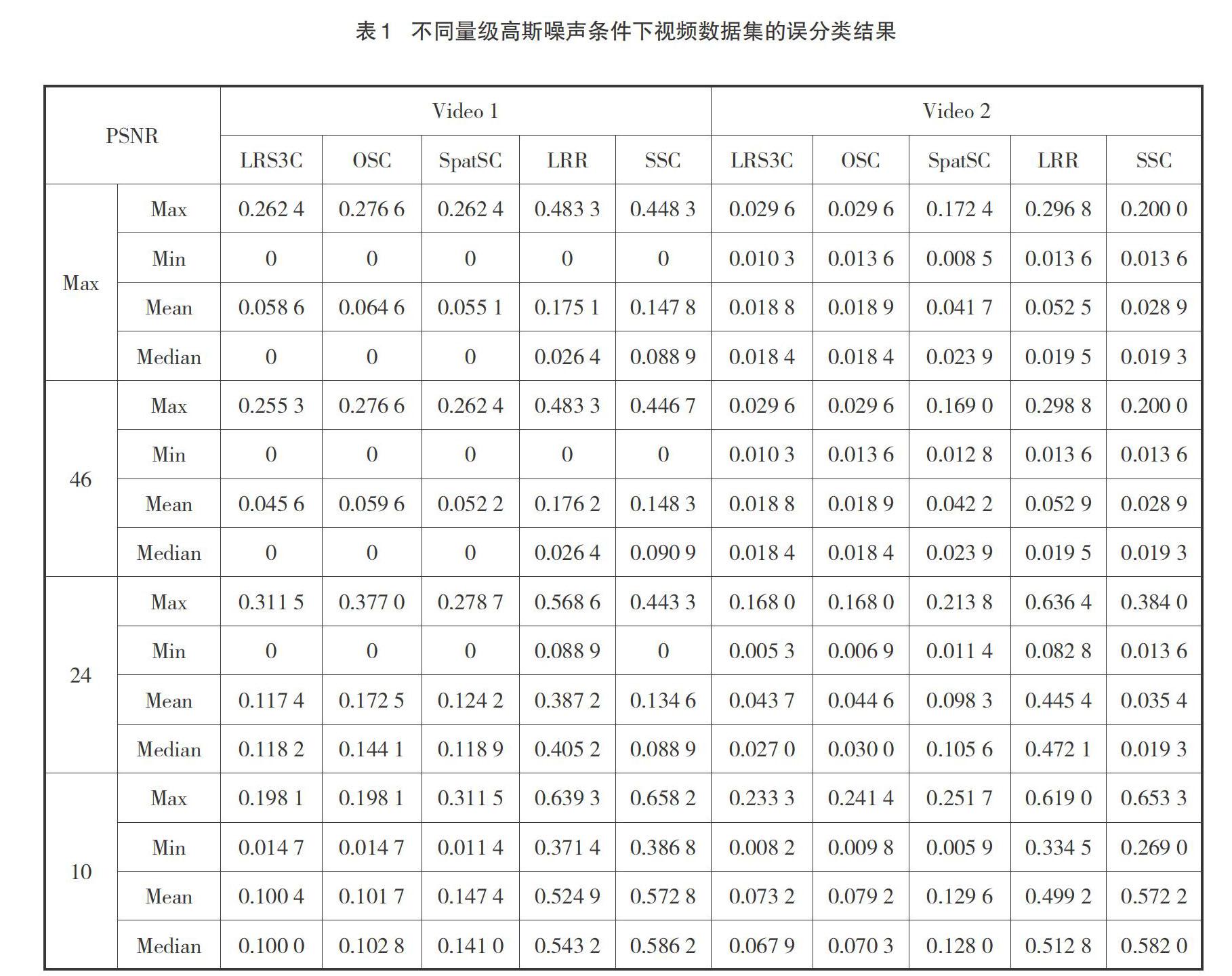
在视频序列被不同程度的高斯噪声污染的条件下,评估了各算法的聚类性能,表1提供了聚类结果。从表中可以清楚地看出,在大多数情况下,LRS3C优于其他方法。当噪声增大时,与其它方法相比,LRS3C算法的误差率始终较低。这表明该方法具有较好的鲁棒性。
3.3 人脸聚类
评估LRS3C在人脸图像聚类中的性能,其目的是从一组人脸图像中分割或聚类到不同的个体。虽然人脸聚类问题并不完全符合我们对序列数据的假设。但是,可以使用人脸图像的空间信息,因为每个数据向量的邻居可能属于同一类。从扩展的YaleB数据集[14]中提取数据,该数据集由38名受试者在不同光照下的大约64张照片组成。图4提供了数据集的图像样本示例。对于每次实验,从数据集中随机选择3名受试者,并在每个受试者中随机排列图像的序列。在实验中,将图像重新采样到[42×48]形成数据向量[Xi∈R2 016]并连接在一起,以确保受试者不会混合。
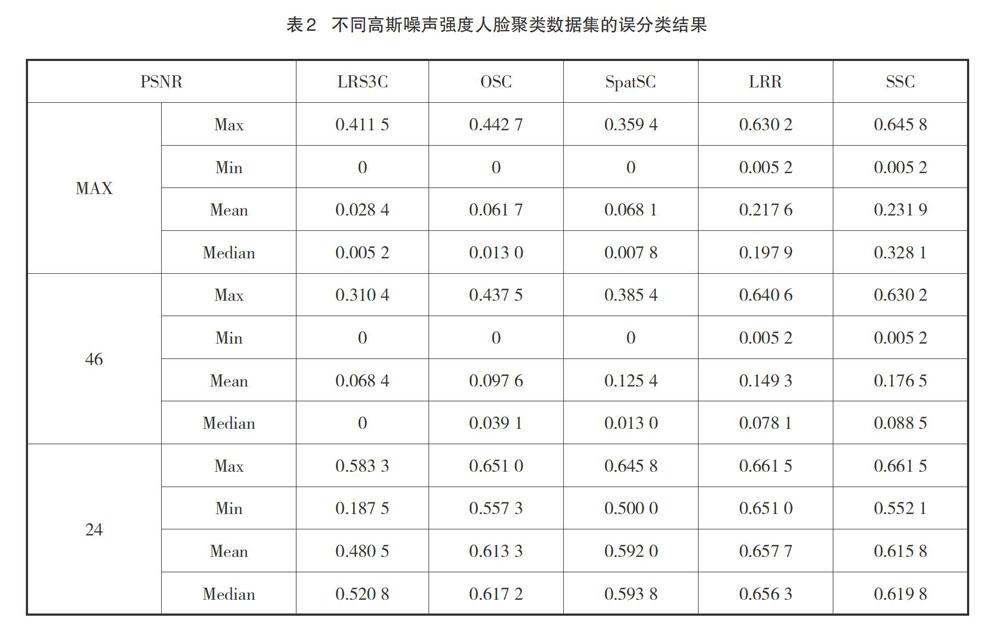
在不同的高斯噪声水平下重复了50次实验。各算法聚类结果如表2所示。
从表2可以看出,在大多数情况下,LRS3C优于其他方法。随着噪声强度的增加,算法的精度不断下降。与其他方法相比,LRS3C方法更穩定,表现更可预测,尤其是在噪声较大的情况下。这证明本研究提出的算法在实际应用中更有效。
4 结论
为了有效地解决序列数据的聚类问题,本文提出了利用给定数据的低秩表示和稀疏表示的LRS3C方法。该方法根据序列数据的连续性特点,利用稀疏表示和低秩表示,进行子空间聚类。在人工数据集和实际数据集上的实验结果表明,与几种最新的子空间聚类方法相比,本文提出的方法是有效的。
参考文献:
[1] VIDAL Rene, MA Yi, SASTRY Shankar. Generalized principal component analysis (GPCA)[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2005, 27(12):15.
[2] LIU Guangcan, LIN Zhouchen, YU Yong. Robust subspace segmentation by low-rank representation[C]//ACM.The 27th International Conference on Machine Learning, June 21-24, 2010, Haifa, Israel: 663-670.
[3] ELHANIFAR Ehan, VIDAL Rene. Sparse subspace clustering[C]//IEEE.2009 IEEE Conference on Computer Vision and Pattern Recognition, June 20-25, 2009, Miami, FL, USA: 2790-2797.
[4] ELHANIFAR Ehsan, VIDAL Rene. Sparse Subspace Clustering: Algorithm, Theory, and Applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11):2765-2781.
[5] LIU Guangcan, LIN Zhouchen, YAN Shuicheng. Robust Recovery of Subspace Structures by Low-Rank Representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 171-184.
[6] FAVARO Paolo, VIDL Rene, RAVICHANDRAN Avinash, et al. A closed form solution to robust subspace estimation and clustering[C]//IEEE. 2011 IEEE Conference on Computer Vision and Pattern Recognition, June 20-25, 2011, Providence, RI, USA:1801-1807.
[7] BOYD Stephen, PARIKH Neal, CHU Eric, et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[J]. Foundations & Trends in Machine Learning, 2010, 3(1):1-126.
[8] GUO Yi, GAO Junbin, LI Feng, et al. Spatial subspace clustering for hyperspectral data segmentation[C]//IEEE.2013 International Conference on Digital Information Processing and Communications, January 30-February 1, 2013, Dubai, UAE: 180-190.
[9] TIERNEY Stephen, GAO Junbin, GUO Yi, et al. Subspace Clustering for Sequential Data[C]//IEEE.2014 IEEE Conference on Computer Vision and Pattern Recognition, June 23-28, Columbus, OH, USA:1019-1026.
[10] WANG Yuxiang, XU Huan, LENG Chenlei. Provable Subspace Clustering: When LRR meets SSC[J].IEEE Transactions on Information Theory, 2019, 65(9):5406-5432.
[11] FRANCIS Bach, RODOLPHE Jenatton, JULIEN Mairal, et al. Convex optimization with sparsity-inducing norms[J]. In Optimization for Machine Learning, 2011:19-49.
[12] LIU Jun, YE Jieping. Efficient L1/Lq Norm Regularization[J]. Computer Science, 2010 ,arXiv:1009.4766.
[13] SHI Jianbo, MALIK Jitendra. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905.
[14] GEORGHIADES Athinodoros S, BELHUMEUR Peter N, KRIEGMAN David J. From few to many: illumination cone models for face recognition under variable lighting and pose[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 23(6):643-660.
責任编辑 祁秀春

