基于分段设计的动力翼伞轨迹规划
朱二琳 高海涛 赵俊杰

摘 要:针对动力翼伞的飞行特点,对飞行及回收过程的轨迹规划问题进行研究。根据实际飞行工况,在传统翼伞轨迹规划中,加入了动力翼伞的任务执行阶段。根据各阶段的几何关系,将轨迹规划问题转换为几何参数的寻优问题。以动力翼伞的回收精度最优作为优化目标,采用量子遗传算法对目标函数进行寻优计算,得出各段轨迹的几何参数。仿真分析验证了该设计方法的可行性和有效性。
关键词:动力翼伞;轨迹规划;分段设计;量子遗传算法
中图分类号:V455.2 文献标识码:A 文章编号:2095-7394(2020)04-0028-08
动力翼伞作为一类新型的柔性飞行器,在传统翼伞系统的基础上加入了动力推进装置,与传统翼伞相比,除了能够完成滑翔和转弯运动,它还能在空中维持高度、甚至爬升[1]。凭借这些优良的飞行特性,目前动力翼伞在军事侦察、农业播撒、广告宣传等领域得到了广泛的应用。
传统翼伞的归航方法一般分为三种[2-6]:简单归航法(包括径向归航和带盲区的锥形归航)、最优控制归航法、分段归航法。20世纪90年代以来,分段归航法以其方法简单、易于实现的特点被广泛地应用于实际工程。根据翼伞自身的飞行特性,将翼伞从投放到着陆的整个过程分为几个阶段,再根据各个阶段的特点,进行分段轨迹的设计,这就是工程中普遍应用的翼伞分段归航法。熊菁对传统翼伞的分段归航做了详细介绍,采用改进的遗传算法对分段轨迹进行优化[7]。张兴会考虑了能量最优,提出了基于能量约束的分段轨迹优化方法,既保证了着陆精度又节省了能量消耗[8]。然而,目前对于动力翼伞的轨迹规划问题还没见到相关的研究文献。
近年来,随着航空航天科技的发展,对翼伞自主归航的要求越来越高,而飞行前的轨迹规划有利于能耗的降低及回收,特别是对于动力翼伞,其所执行的任务并不仅限于物资的空投和回收,所以有效的轨迹规划显得尤为重要。本文采用量子遗传算法研究了基于分段设计的动力翼伞的轨迹规划问题,并通过仿真对所提算法的可行性进行了验证。
1 动力翼伞质点模型
对于飞行器的轨迹规划问题,复杂的动力学模型将增加运算的复杂度,会影响轨迹的准确性[9]。本文采用较为简单的3自由度质点模型,在建模之前,先做如下几点基本假设:
(1)在飞行过程中,将动力翼伞看作一个质点,不考虑姿态的变化,水平速度保持不变;
(2)在任务执行阶段,动力翼伞等高飞行,垂直速度为零,在其他阶段,垂直速度为定值;
(3)只考虑水平面的风场,且风场信息已知。
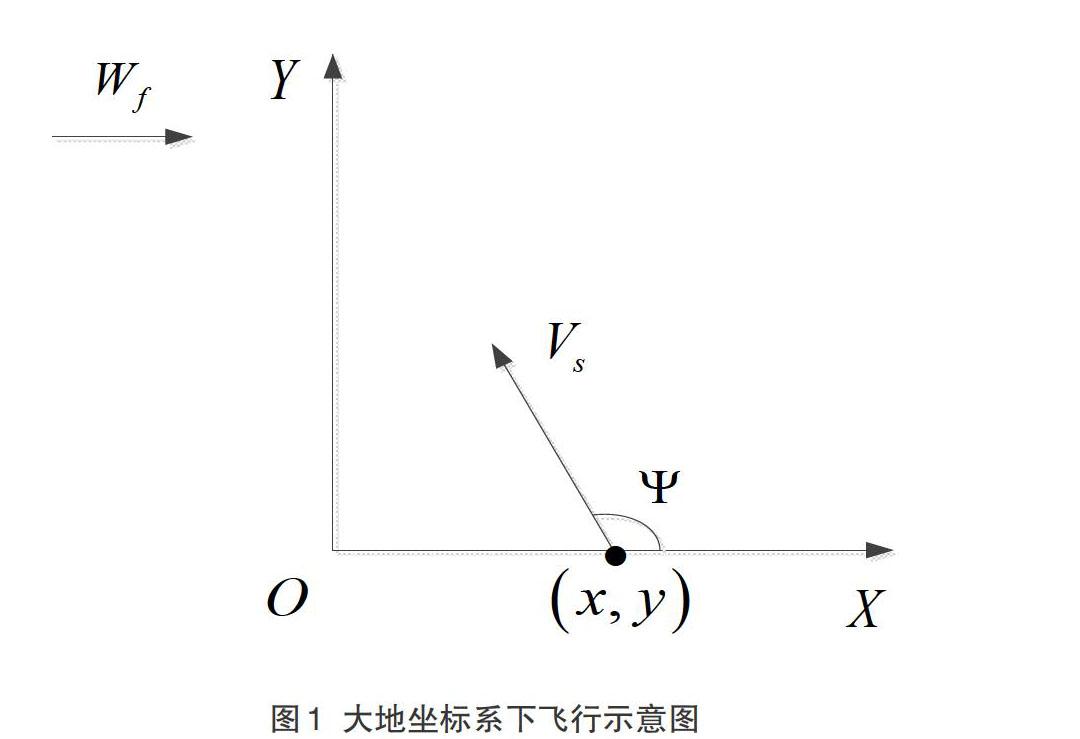
如图1所示为动力翼伞水平面的飞行示意图,大地坐标系原点为着陆的目标点,X轴的方向同风场方向保持一致,Z轴方向垂直向下,Y轴同X轴、Z轴共同构成右手坐标系。
根据飞行示意图,可将动力翼伞模型简化成如下形式:
其中:([x y z])代表动力翼伞在大地坐标系下的位置;[Vs]和[Vz]分别代表动力翼伞的水平速度和垂直速度(在任务执行阶段[Vz=0]);[Ψ]代表水平飞行方向同大地坐标系X轴之间的夹角;[Ψ]代表转弯角速度;[u]代表伞绳控制量(同转弯角速度之间存在对应关系);[W]代表水平风场信息。
对于动力翼伞而言,任务执行段的轨迹应是固定不变的,不能随风产生漂移,所以动力翼伞的轨迹规划问题不能在风坐标系下进行讨论。本文的研究基于上述的大地坐标系,在轨迹规划过程中,不考虑风的因素。
2 动力翼伞分段轨迹设计
2.1 分段策略
传统翼伞的归航轨迹可大致分为三个阶段[7]:向心段,从翼伞初始投放点到着陆区域;能量控制段,在着陆区上空盘旋削高直到满足一定高度条件;着陆段,寻找逆风方向、滑翔,最后进行雀降。对于动力翼伞的轨迹规划问题,是在传统翼伞的归航过程中加入特定的任务执行段,当任务执行完毕后再进行归航。动力翼伞目前主要应用于特定的工况,通常将动力翼伞的任务执行阶段设定为拥有固定圆心和半径的圆。
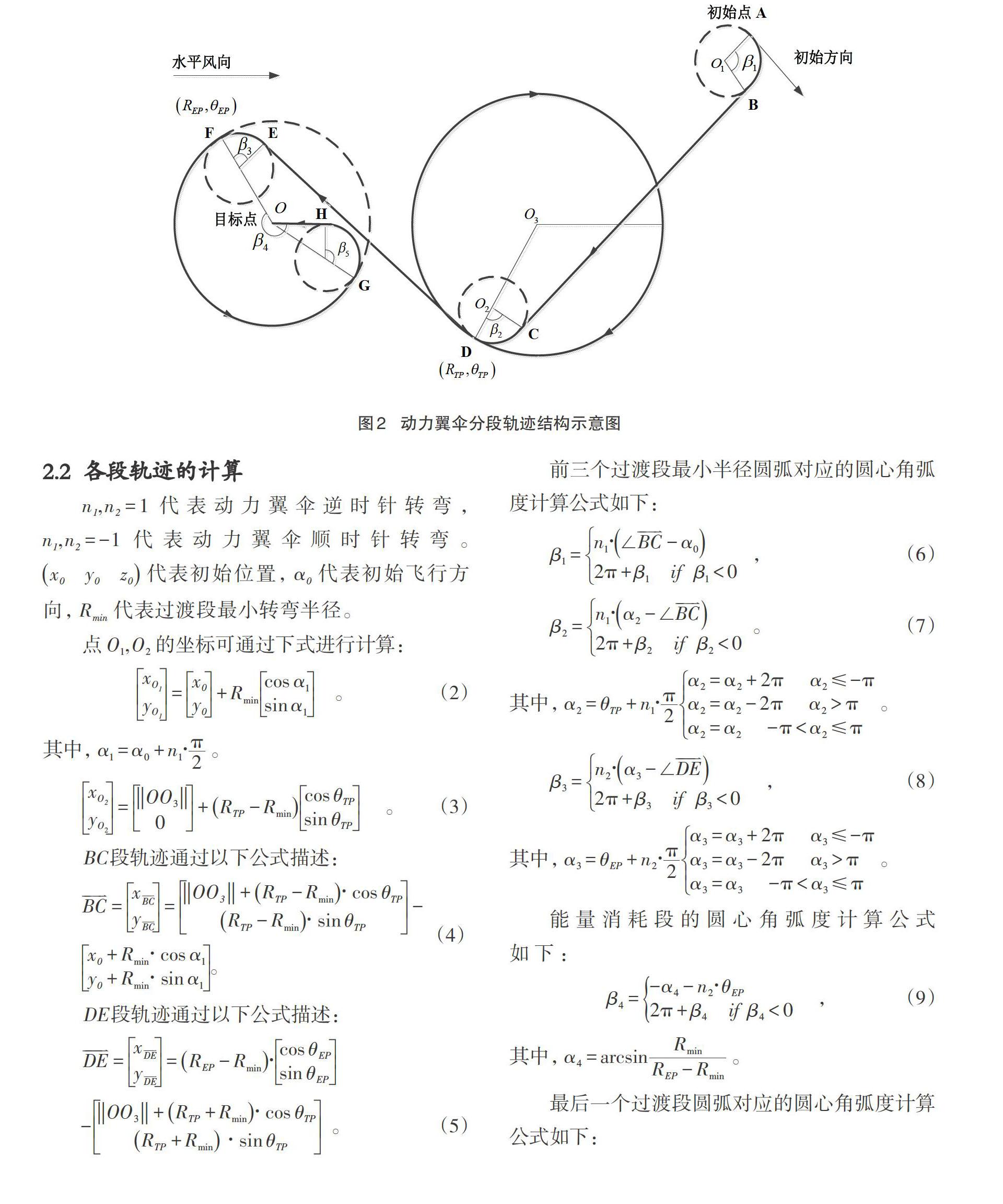
动力翼伞水平方向运动只能通过单拉伞绳和双拉伞绳来进行控制,所以动力翼伞水平面的轨迹可以看作是直线和圆弧的组合。图2为动力翼伞分段轨迹的结构示意图。
如图2所示,A点是动力翼伞的初始点,O点是着陆的目标点,BC段和DE段是动力翼伞的向心段,分别对应任务执行区域和着陆区域。以[O3]点为原点、[RTP]为半径的圆形轨迹为动力翼伞的任务执行阶段,此阶段动力翼伞高度保持不变。FG段为能量控制段,此阶段动力翼伞盘旋削高。HO段为着陆阶段。AB、CD、EF、GH段为各阶段的过渡阶段,动力翼伞以最小的转弯半径转弯飞行。[βii=1,…,5]代表最小半径圆弧对应的圆心角弧度。根据各段轨迹的几何关系,动力翼伞轨迹规划的关键就是确定任务执行段的进入点D和能量消耗段的进入点F。R代表圆弧的半径,[θ]代表进入点和对应阶段圆的原点连线同大地坐标系X轴正向的夹角。下标TP代表任务执行段进入点,EP则代表能量控制段的进入点。[RTP]根据实际工况可事先设定,所以待优化的轨迹参数为[θTP,REP,θEP]。
2.2 各段轨迹的计算
[n1,n2=1]代表动力翼伞逆时针转弯,[n1,n2=-1]代表动力翼伞顺时针转弯。[x0y0z0]代表初始位置,[α0]代表初始飞行方向,[Rmin]代表过渡段最小转弯半径。
2.3 目标函数
动力翼伞归航同传统翼伞类似,需要保证以下两点:(1)着陆点距目标点误差最小;(2)着陆方向为风向的反方向。在分段轨迹设计中已經考虑了逆风对准,所以动力翼伞轨迹规划的目标函数选择为从初始点到目标点飞行的水平面轨迹同定滑翔比条件下初始高度对应的水平距离之间偏差的绝对值。由于动力翼伞在任务执行段飞行高度保持不变,因此,在目标函数中这一阶段的水平面轨迹可忽略。
目标函数如下式所示: [J=Rmin?β1+β2+β3+β5+REP?β4+BC+DE+REP-2Rmin?REP-f?z0] 。 (11)
其中:[f]代表滑翔比,[f=Vs/Vz],[z0]代表初始高度。分段轨迹的参数变量为[θTP,REP,θEP],以下通过参数寻优的方法对轨迹规划问题进行求解。
3 量子遗传算法
量子遗传算法(Quantum genetic algorithm,QGA)[10-12]是量子计算和遗传算法相结合的产物。染色体在编码过程当中,引入量子的概率幅表示方法,从而使每个染色体能够表示多个状态的叠加。通过量子旋转门策略对染色体进行更新,可达到对目标函数的最优求解,因此,只要是遗传算法能够求解的优化问题,都可以用量子遗传算法来解决。
对于上文描述的动力翼伞分段轨迹优化问题,目标函数如式(11)所示,这是一个标准的多变量参数寻优问题,很适合用量子遗传算法来进行求解计算。根据上述问题描述,优化的参数变量为[θTP,REP,θEP]。转弯方向根据初始点位置的不同可有不同的组合方式,在优化之前进行确定,针对不同的[n1,n2]值分别对目标函数进行量子遗传算法的求解,并选取最优的解。
量子遗传算法对分段轨迹参数寻优的具体步骤如下:
(1)采用小生境协同进化策略,对种群[Q(g0)]进行初始化;
(2)测量种群[Q(g0)]中每个染色体,可得二进制编码;
(3)计算目标函数,对种群[Q(g0)]中所有个体逐个进行适应度的评价;
(4)选择适应度最优的个体,并保存相应的适应度值;
(5)判断是否满足结束条件,如果是,转向步骤(11);
(6)测量种群[Q(g)]中每个染色体,得到二进制编码;
(7)对种群[Q(g)]中所有个体逐个进行适应度的评价;
(8)通过量子旋转门对种群[Q(g)]进行更新,得到下一代的种群[Q(g+1)];
(9)选择适应度最优的个体,并保存相应的适应度值;
(10)转向步骤(5);
(11)将优化所得的最优参数[θTP,REP,θEP]代入相应的公式,得到各段的轨迹;
(12)结束。
4 仿真分析
以动力翼伞的质点模型为基础,本节对所提出的分段轨迹优化方法进行仿真验证。动力翼伞的水平速度[Vs=13.8 m/s],无动力驱动时垂直速度[Vz=4.6 m/s],滑翔比 [f]=3。动力翼伞任务执行段轨迹圆心坐标为(1 000,0)[m],半径[RTP=500 m],[Rmin=100 m]。约束条件[REP∈230500 m,][θTP,θEP∈-ππ],[βi(i=1,…,5)∈0π]。
(1)动力翼伞初始位置:[x0 y0 z0=1 850 600 1 380 m],初始飞行方向:[Ψ0=-π/3]。
通过量子遗传算法的求解计算,所得最优参数:[θTP=-2.25],[REP=300 m],[θEP=2.34]。
仿真结果如图3所示。
由图3(a)动力翼伞的水平面飞行轨迹不难看出:动力翼伞首先由初始点飞翔至任务区域,由任务段进入点([θTP=-2.25])开始任务执行阶段;然后动力翼伞开始归航,进行回收,由能量控制段进入点([REP=300 m],[θEP=2.34])进行盘旋削高;最后,逆风对准,滑翔着陆。整个过程是满足动力翼伞飞行和归航特点的。由图3(b)的侧向面轨迹图可以看出:当动力翼伞着陆时,恰好达到目标点,着陆误差为0.41 m。如图3(d)所示为左右伞绳的控制量[u],控制量的定义见公式(1),正值代表右转,负值代表左转,分段轨迹的控制曲线为分段的直线。通过电机带动下拉伞绳,能够避免执行机构频繁的动作,在降低能耗的同时也有利于系统的稳定性,从而更加切合实际的工程应用。
(2)动力翼伞初始位置:[x0 y0 z0=200 600 1 380 m],初始飞行方向:[Ψ0=-2π/3]。
通过量子遗传算法的求解计算,所得最优参数:[θTP=-2.15],[REP=302.3 m],[θEP=1.44]。
仿真结果如图4所示。
当动力翼伞初始位置发生变化,仍然能规划出一条合理的轨迹,最终的着陆精度为0.38[m] ,说明了分段轨迹设计方法的鲁棒性。
5 結论
本文主要对动力翼伞的分段轨迹规划相关问题进行了研究。在传统翼伞分段归航过程中,加入了动力翼伞的任务执行阶段,当动力翼伞完成任务执行阶段之后,进行归航回收阶段。根据各分段轨迹的几何关系,将轨迹规划问题转换成参数寻优问题;采用量子遗传算法对分段轨迹的目标函数进行求解计算,得到设计参数的最优值,将最优参数代入计算出各分段轨迹,获得动力翼伞总的飞行轨迹。
上述研究中,动力翼伞的垂直下降速度在任务执行阶段为0,在其他阶段为固定不变的值,后续的研究中还会将动力翼伞垂直速度的变化情况考虑进去。此外,目标函数主要基于着陆误差而建立,并没有考虑控制能量的约束,但在实际飞行过程中,动力翼伞携带的能量是有限的,对于这一问题也将在后续的研究中予以解决。
参考文献:
[1] ZHU E L,SUN Q L,TAN P L,et al. Modeling of powered parafoil based on Kirchhoff motion equation[J]. Nonlinear Dynamics, 2015,79(1):617-629.
[2] PEARSON A E, WEI K C,Koopersmith R M. Terminal control of a gliding parachute in a nonuniform wind[J]. AIAA Journal,1977,15(7):916-922.
[3] 熊菁,秦子增,文红武.翼伞系统归航的最优控制[J].航天控制,2004,22(6):32-36.
[4] 焦亮,孙青林,亢晓峰.基于混沌粒子群优化算法的翼伞系统轨迹规划[J].复杂系统与复杂性科学,2012,9(1):47-54.
[5] ZHANG L M,GAO H T,CHEN Z Q,et al. Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method[J]. Nonlinear Dynamics,2013,72(1-2):1-8.
[6] TAO J,SUN Q L,ZHU E L,et al. Quantum genetic algorithm based homing trajectory planning of parafoil system[C]. Hangzhou:Proceedings of the 34th Chinese Control Conference,2015:2523-2528.
[7] 熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙:国防科技大学,2005.
[8] 张兴会,朱二琳. 基于能量约束的翼伞系统分段归航设计与仿真[J]. 航天控制,2011,29(5):43-47.
[9] SAUNDERS D,ALLEN G,GAGE P,et al. Crew transfer vehicle trajectory optimization[C]. Anaheim:35th AIAA Thermophysics Conference,2001:2001-2885.
[10] YANG J A,LI B,ZHUANG Z Q. Research of quantum genetic algorithm and its application in blind source separation[J]. Journal of Electronics,2003,20(1):62-68.
[11] 傅德勝,张蓉. 一种改进的量子遗传算法研究[J]. 计算机仿真,2013,30(12):321-325.
[12] 刘振,彭军,刘勇.小生境分布估计量子遗传算法及其仿真分析[J]. 计算机工程与科学,2016,38(1):89-94.
责任编辑 盛 艳

