GNSS辅助伪卫星系统定位初始值滤波算法与二阶数字滤波器设计


摘 要:全球卫星导航系统(GNSS)辅助地基伪卫星定位的主要目的是解决工程实际应用中的一些问题。在地基伪卫星应用于码头港口等环境较为复杂的场景时,因为基站距离地面较近,多径现象较为严重,给固定整周模糊度带来了困难,无法得到准确的初始值。以GNSS与惯性导航系统组合定位模式为参考,对GNSS辅助伪卫星系统定位初始值的工作方案进行了研究,比较了算术平均值滤波、中值滤波等常用一阶数字滤波器的优缺点,并通过分析多组GNSS静态定位的误差,设计了一种二阶数字滤波器。试验结果表明,二阶滤波器的滤波效果达到了伪卫星初始值定位的精度要求,能够在工程上解决伪卫星的初始值问题。
关键词:GNSS辅助伪卫星系统;惯性导航系统;初始值;二阶数字滤波器
中图分类号:TN713;TP273 文獻标识码:A 文章编号:2095-7394(2020)04-0036-07
惯性导航系统(Inertial Navigation System,INS,简称“惯导系统)是本世纪初发展起来的导航技术,具有自主性强,不受环境、载体本身的运动和无线电的干扰,可输出全部导航参数,实时数据更新率高,短期的精度和稳定性出色等特点。[1]由于惯导系统的这些优点,加上高精度的惯导设备的价格逐步降低,其目前已被广泛应用于航空、航天、航海等领域。INS的工作模式主要是通过高精度陀螺仪传感器得到的加速度和角速度积分获取位置、速度、姿态等参数,这些参数的误差会随着导航时间的延长而累积,经过一段时间后变得完全无法使用。而全球卫星导航系统(Global Navigation Satellite System,GNSS)的误差不会随着时间的延长而变化,而且在GNSS信号受到遮挡时,短时间内惯导系统可以提供精度足够的定位结果。因此,GNSS与惯导系统的组合成为许多惯导系统提高自身性能的选择。
根据使用的观测值以及GNSS与INS相互辅助关系的不同,GPS/INS的组合模式主要分为三种:基于GNSS导出的位置速度的松组合、基于GNSS原始观测值的紧组合和INS辅助GNSS的深组合。[2]松组合是GNSS与INS最简单的组合模式。INS与GNSS各自独立工作然后将导航的位置差和速度差作为组合滤波的输入函数。松组合方式的优点是结构简单易于实现,可以提高定位连续性和稳定性。但若长时间无法接收到4颗GNSS卫星,则无法得到GNSS的导航信息来对滤波器进行更新,整体导航性能就会累积误差而变得很差。紧组合模式相比松组合是一种相对复杂的组合模式,它在GNSS可见卫星数目少于4颗但不少于1颗的情况下,仍可输入观测值到滤波器进行更新,从而限制INS的误差积累,拥有更好的定位精度和稳定性,因此更加适合城市、峡谷等卫星容易遮挡的应用场景。不过紧组合定位需要建立比松组合更加复杂的系统模型和观测模型,计算量更大,滤波器的收敛速度会较慢。深组合则使用INS输出经过修正的导航参数来辅助GNSS跟踪环路,是一种在硬件层面更深层次的组合方式,具备强大的动态性能和抗干扰能力,更多用于军事领域。
GNSS/INS作为GNSS辅助其他定位系统的一个典型应用,对GNSS辅助地基伪卫星的初值定位的组合模式起到了参考作用。GNSS辅助伪卫星初始值定位的精度会直接影响伪卫星后续定位的精度,在设计定位初值的组合模式时,需要采用数字滤波器提高初始值的精度,进而提高整个系统的定位精度。笔者拟在比较算术平均值滤波、中值滤波等常用一阶数字滤波器优缺点的基础上,设计一种能满足伪卫星初始值精度要求的二阶数字滤波器,并在试验平台比较验证其有效性。
1 伪卫星初始值
GNSS和伪卫星系统实现高精度定位的关键技术就是载波相位整周模糊度的固定。只有正确获取模糊度的整数解,载波相位观测量才可以成为用于定位解算的高精度测量值。[3]整周模糊度的求解通常分为两步进行:(1)通过一定的算法求解出整周模糊度;(2)验证所得到的整周模糊度的准确性。GNSS的整周模糊度有多种方法用于固定,常用的静态观测法是将接收机放在一个固定的位置上,经过多历元的观测,当观测量达到一定程度就可通过载波相位观测方程实现对整周模糊度的计算。静态观测法的运用需要建立在卫星不同历元的运动使得构建的载波相位方程不共线的基础上。由于伪卫星的基站是固定不动的,几何多样性不足,因此无法使用静态观测法进行整周模糊度的固定。另一种GNSS解决整周模糊度的在航解算法,因为伪卫星的基站距离地面高度不高,多径效应比GNSS严重很多,使得整周模糊度的固定极为困难。由于这些原因,工程应用中地基伪卫星系统通常采用静态初始化法(Known Point Initialization,KPI)来固定整周模糊度。
1.1 静态初始化法
静态初始化法(Known Point Initialization,KPI)是接收机在地面固定且基站固定不动的前提下,测定接收机的具体坐标,计算出接收机与基站的距离,并带入观测方程解出整周模糊度的方法。为了消除接收机的时钟误差,地基伪卫星使用了单差分技术。在式(1)和(2)中,对流层误差通过了一个校正模型来拟合,假设以接收机接收基站[i]的信号作为参考信号,接收到节点[j]的为另一组信号,则单差分方程由式(1)与(2)相减所得,如式(3)所示。
假设接收机在[t]时刻的坐标为[xut,yut,zut,]两个基站的坐标分别是[xi,yi,zi,][xj,yj,zj]。式中[ρij]代表距离差,如式(4)所示。
其中:[ΔNij]表示单差模糊度,[τijt]表示对流层延时的差值,[v=εi-εj]是噪音误差的差值。接收机的坐标是已知的,所以当忽略噪声和使用模型修正过对流层误差后,可以算出[ΔNij],如式(5)所示。
由式(5)可以看出,当测定的接收机坐标越接近真实值,解算出的整周模糊度就越准确,伪卫星的定位精度也就更高。所以,一个高精度的初始值是地基伪卫星系统性能的保障。在应用中,伪卫星的初始值也都是经过精确测量后输入系统的。
1.2 初始值的获取
在工程实际应用中,每次定位前都人为地对接收机的精确坐标进行测算,是不符合工程实际需求的。因为接收机的位置不一定方便进行测量,而且每次使用都进行初始值的测量也影响产品的使用体验。参考GNSS/INS组合定位模式,GNSS辅助INS可以很好地弥补INS随着时间的增加误差不断累积的缺点,提高系统的精度。在地基伪卫星的应用中,GNSS的多径效应没有地基伪卫星严重,整周模糊度的解算难度相较伪卫星成功率更高,而且GNSS短时间内的静态定位精度可以达到厘米级。因此,可以利用GNSS测定地基伪卫星接收机的位置,对测定的多组数据进行数字滤波后作为地基伪卫星的初始值输入系统,最终解算出地基伪卫星的整周模糊度,让地基伪卫星成功开始定位。给定初始值后,即使GNSS出现可见星数不足导致精度不够的问题,也不会影响伪卫星的精度。而且在组合定位成为地基偽卫星研究重点的现在,系统融合GNSS不会在工程上有困难。所以,GNSS辅助地基伪卫星获取初始值可以成为一个符合工程实际应用的解决方案。
2 GNSS辅助伪卫星初始值定位方案
2.1 组合方式
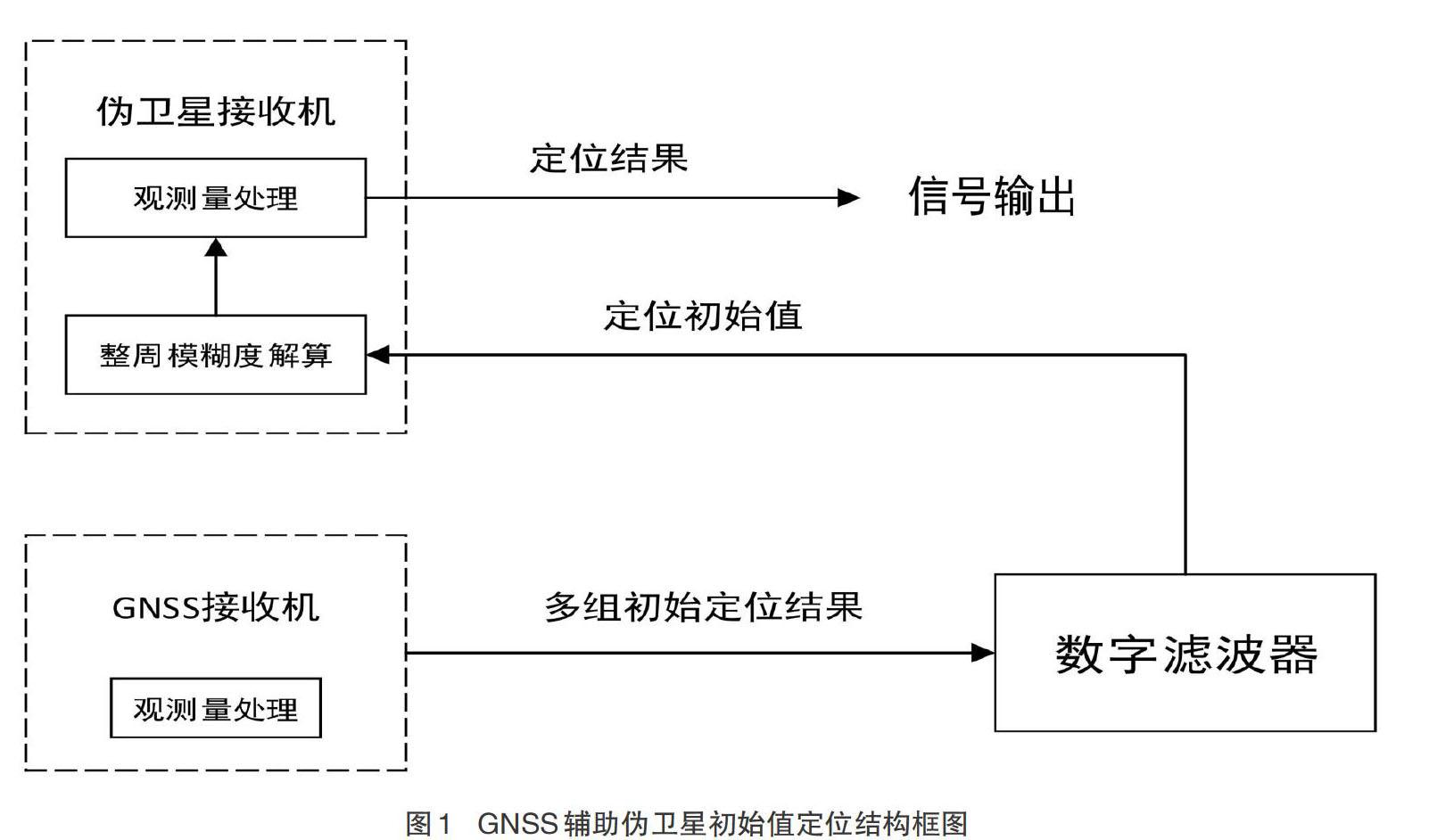
在确定了GNSS辅助伪卫星的方案后,对GNSS与地基伪卫星定位初始值的组合模式进行了设计。组合方式如图1所示。
GNSS辅助地基伪卫星初始值定位过程需要在系统运行之后,先保证伪卫星接收机处于静止不动的状态;伪卫星系统会等待GNSS发送定位初始值和可开始定位的标志位;在GNSS获取到足够多的定位初始值之后,将多组数据输入到数字滤波器进行处理,再将滤波后的结果和可开始定位的标志位发送给伪卫星定位解算模块,伪卫星的定位解算模块接收到初始值后,使用静态初始化法进行整周模糊度的解算;在解算出整周模糊度后,伪卫星接收机便可开始运行,进行动态定位。
2.2 数字滤波器
使用静态初始化法进行整周模糊度的解算对初始值的精度要求较高。虽然GNSS的静态定位精度可以达到厘米级,但是为了获取更加准确的初始值,既需消除一些硬件噪声和环境的电磁干扰对定位结果的影响,还需对GNSS的输出数据进行数字滤波之后再作为伪卫星初始值。为了得到更为精确的初始值,提高整个系统的定位精度,下文将比较算术平均值滤波、中值滤波等常用一阶数字滤波器的优缺点,并通过分析多组GNSS静态定位的误差,设计一种能达到伪卫星定位初始值精度要求的二阶数字滤波器。
2.2.1算术平均值滤波
算术平均值滤波是最为常用的数字滤波器,算法原理是按照输入的[N]个采样数据[xi=i=1~N],寻找一个[y],使[y]与各个采样值的偏差平方和最小,公式为:
通过式(6)求极值可以得出[y=i=1Nxi/N],与采样值的算术平均值的算法公式相同,这个方法是将[N]次采样值相加,取其算术平均值作为采样值。
随机干扰信号的特点是在某一数值附近范围作上下波动,如果仅采用一次采样的值作为最终的结果显然是不准确的,工程上通常采用算术平均值滤除随机干扰信号。但是算术平均滤波器输出会引入脉冲带来的误差,无法有效滤除脉冲性干扰,因此,不适合脉冲干扰严重的场合。算术平均滤波器对信号的平滑程度取决于[N]。当[N]较大时,平滑度高,但灵敏度低,外界信号的变化对测量结果[Y]影响小;当[N]较小时,平滑度低,但灵敏度高。[4]对于伪卫星系统初始值来说,只需要输出一组定位结果,对滤波算法的灵敏度没有要求。所以,伪卫星初始值定位选用算术平均值滤波器,将[N]设为能采集到的有效数据的数量。
2.2.2中值滤波
中值滤波是对某一被测参数连续采样[N]次([N]一般为奇数),然后将[N]次采样的值按照大小进行排序,在重新排列的序列中取其中间值作为本次采样值。设有采样值序列[x1,x2,…xi],长度为[N],计算方法如下。
(1)首先利用排序算法将序列[xi]重新排列,生成新的序列为[y1,y2,…yi]。
(2)计算[N/2]的值。若能够整除,说明[N]为偶数;若不能够整除,则对[N/2]进行取商的运算,将[N/2]的值记为[k]。
(3)当[N]为偶数时,最终输出值[z=yk+yk+1/2];当[N]为奇数时,最终输出值[z=yk]。[5]
中值滤波对于去掉偶然因素引起的波动,或者采样器硬件本身不稳定所造成的误差而引起的脉冲干扰比较有效。对于伪卫星初始值定位的滤波而言,是一个具有可用性的数字滤波器。
2.2.3二阶滤波
二阶数字滤波器应用于GNSS辅助伪卫星系统初始定位中,也称为伪卫星初值滤波器,其滤波流程如图2所示。[6]GNSS将静态定位结果输入到算术平均值滤波器内,算术平均值滤波器的[N]设为10,在收集到10组定位结果后,将滤波值输入到二阶中值滤波器内,中值滤波器的[N]也设置为10。在中值滤波器也进行了滤波之后,将滤波值作为定位初始值输入到伪卫星系统中。得到一个滤波后的定位初始值,需要100组GNSS静态定位的值。GNSS设定为每5 s将一个定位值输入到滤波器内。通过计算可知,得到初始值的时间为500 s,再加上GNSS捕获跟踪信号所需要的时间(一般不超过30 s),得到一个高精度的定位初始值的时间不会超过600 s。这个时间在高精度定位领域是可以接受的。
3 试验与分析
为了实测二阶滤波器与常用一阶滤波器的滤波效果,对二阶滤波器(伪卫星初值滤波器)、算术平均值滤波器、中值滤波器的滤波效果在10个测试地点进行了测试。对滤波后的定位结果与真实坐标的差值做出了统计,图3、图4、图5给出了3种数字滤波后定位结果的误差。
从图3、图4、图5可以看出: 二阶滤波器滤波结果的误差在大部分的测试点都表现比另外两种一阶数字滤波器的误差更小,在个别测试点的误差会比另外两种一阶滤波器稍大。总体上,二阶滤波器的滤波效果达到了伪卫星初始值定位的精度要求,能够在工程上解决伪卫星的初始值问题。
4 结语
为了解决地基伪卫星定位系统由于多径效应引起的初始值定位困难问题,按照GNSS的整周模糊度解算原理并参考了GNSS与INS的组合定位方式,提出了GNSS辅助伪卫星初始值定位的方案。初始值的精度会影响伪卫星后续定位的精度,对GNSS定位结果进行二阶滤波相较于常用的一阶滤波可以提高初始值的精度,进而提高整个系统的定位精度。GNSS辅助伪卫星系统的组合不但在工程上解决了定位初始值问题,提高了伪卫星系统的实用性,也为后续两个系统的组合定位奠定了基础。
参考文献:
[1] 陈展,王欣.惯性/星光组合导航系统在临近空间高超声速飞行器上的应用研究[J].飞航导弹,2020(4):90-95.
[2] 刘帅. GPS/INS组合导航算法研究与实现[D].郑州:解放军信息工程大学,2012.
[3] 匡宇龙,王玲,乐乐.地基伪卫星单历元三频组合逐级模糊度解算方法[J].全球定位系统,2020(2):44-48.
[4] 崔建伟.基于嵌入式系统的数字滤波器、倾角传感器设计[D].北京:北京邮电大学,2008.
[5] 牛秀琴.几种改进的中值滤波算法研究[D].成都:四川师范大学,2012.
[6] 高端阳,李安,傅军.一种指数渐消记忆加权滤波的内交点定位算法[J].中国惯性技术学报,2018(3):299-304.
责任编辑 张志钊

