一种基于高效边界探索的机器人自主建图方法
刘瑞雪,曾 碧,汪明慧,卢智亮
(广东工业大学 计算机学院,广东 广州 510006)
随着机器人技术的快速发展和社会需求的变革,自主移动机器人越来越受到工程界和学术界的关注[1]。为使移动机器人能够在非结构化、非确定的环境中自主帮助人们完成日常生活任务,首要实现的关键技术是当机器人处于未知环境时,可自主探索移动路径,并同时利用基于激光传感器的同步定位与建图(Simultaneous Localization and Mapping,SLAM)[2-3]技术建立外界环境在机器人内部表示的地图,用于后续导航[4-5]。但是传统机器人建图的方式是人工手动或使用键盘、游戏杆控制机器人移动,在面对大而复杂的室内环境时会浪费时间、人力、物力[6]。因此使机器人脱离人为控制,实现自主探索建图路径具有重要意义[7-8]。
机器人自主探索建图是一种基于SLAM算法和路径规划算法,自主寻找有建图路径的目标点以探索环境未知区域,实现环境完整构图的方法,涉及机器人定位、构图与路径规划等多方面技术。
在自主探索领域,Yamauchi[9]提出Frontierbased边界探索方法是目前大多数探测算法的基础。Yamauchi定义地图上空闲区域和未知区域之间为地图边界,并不断将机器人移动探索的目标设定为距离机器人最近的边界,该方法可以使机器人完整遍历未知的室内环境。但该方法没有考虑路径最优,因此在未知环境面积比较大的时候,机器人探索会耗费大量时间。为了缩短机器人探索路径,Dirk Holz等[10]提出通过Dijkstra算法更新和存储栅格地图中机器人与所有边界栅格的路径长度,缩短了自主建图的探索路径。但是该方法仅仅考虑了机器人与边界的路径信息,忽略了地图自身携带的有效信息,所以建图时间优化效果一般。为了可以融合地图信息来提高建图效率,文献[11-12]提出了基于地图和路径估计的信息增益的解决方案,该方案将建图路径和地图信息增益最大化作为决策依据,降低了探索建图的执行时间。但是计算信息增益需要大量内存和计算量。考虑到计算量的问题,高环宇等[13]采用一种动态建立待探索边界的探索树以降低地图探索重复率的方式,有效缩短了探索建图时间,但建图过程中探索树的建立不断增加了程序的内存量。类似地,李秀智等[14]将栅格地图和拓扑地图融合,通过标记拓扑节点的状态来减少机器人对环境的重复探索。该方法虽然降低了边界探索算法的重复率,但是对候选边界的评估有所欠缺,容易产生无效不可达边界。
综上可见,国内外学者对自主探索建图算法已有一定的优化效果。但仍存在两个主要问题:第一,自主建图路径探索点选取条件欠缺。探索区选取算法未考虑探索点的可达性和防机器人碰撞的安全性。第二,探索建图时间长,当出现机器人不能导航到探索目标点时,缺乏有效的实时解决方案,往往会增加建图时间。
因此本文提出一种基于曲线拟合和滑动窗口规划的自主边界探索建图方法CS-frontier。以Frontierbased算法为基础,该方法在确定目标探索边界之前,对地图候选边界曲线拟合建模,使机器人自主建图时可不断优选可容纳机器人访问的安全的建图目标探索点,并以最短路径导航到每一个可达目标探索点,同时借助SLAM技术完成构图;同时当出现机器人导航不可达路径的目标探索点时,使用基于滑动窗口边界邻域规划方法及时生成最优可达目标替代点来引导导航和完成最终建图。该方法减少了机器人自主建图的时间,增强了机器人自主建图的鲁棒性和安全性。
1 背景知识
1.1 Frontier-based边界探索算法
Frontier-based边界探索算法[9]思想为:根据已构建的地图环境信息,检测已知地图与未知地图之间的边界,选取与机器人距离最近的边界作为探索目标点;机器人探索完该目标点后,再根据更新的地图确定下一个探索目标点,以此不断迭代,直到完成对所有未知环境的探索。
1.1.1 地图表示
Frontier-based算法采用的地图表示是证据网格(Evidence Grids)[15],如图1所示。证据网格通过传感器的距离数据得到环境的占用状态,提供详细的环境特征数据,是机器人导航和路径规划的重要基础。证据网格中单元格有3种区域:空闲区域,表示单元格处没有障碍物;占用区域,表示单元格处有障碍物;未知区域,表示单元格还未被机器人感知到,属于未知的区域。分别由白色、黑色、灰色表示。
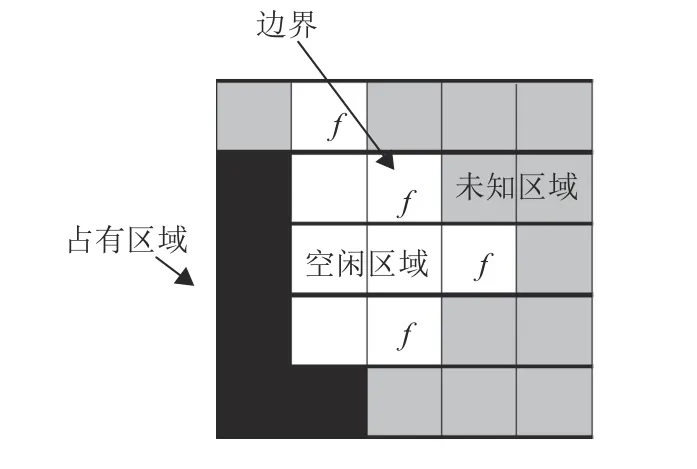
图1 证据网格Fig.1 Evidence grids
1.1.2 边界探索
Frontier-based算法定义:在证据网格中,如图1所示,有 f标识的单元格为边界单元格,相邻的边界单元格组成一条边界。在检测到边界后,将边界长度大于阈值的边界添加到可访问的边界列表中,机器人尝试以最短路径导航到最近边界的质心进行下一步探索。具体探索流程如图2所示。
1.2 最小二乘法曲线拟合原理
曲线拟合是根据两个具有函数关系变量的多组实际值来确定两个变量函数曲线的方法。最小二乘法曲线拟合是使得变量实际值与拟合曲线的因变量的残差平方和最小为优化目标的方法。以下为利用最小二乘法拟合多项式曲线的数学原理。
设两个变量的一组数据x=(x1,x2,···,xn) ,y=(y1,y2,···,yn),两个变量的拟合曲线多项式 p(x)为
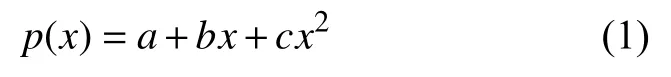
其中a,b,c为多项式未知常量系数,为了求得a,b,c的值,推算过程如式(2)所示。
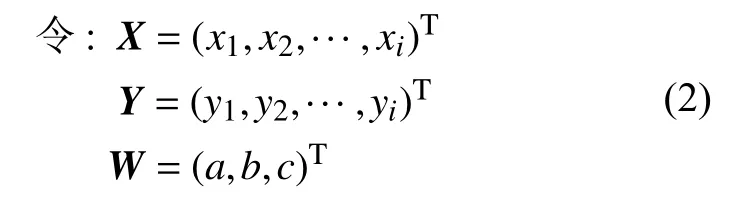
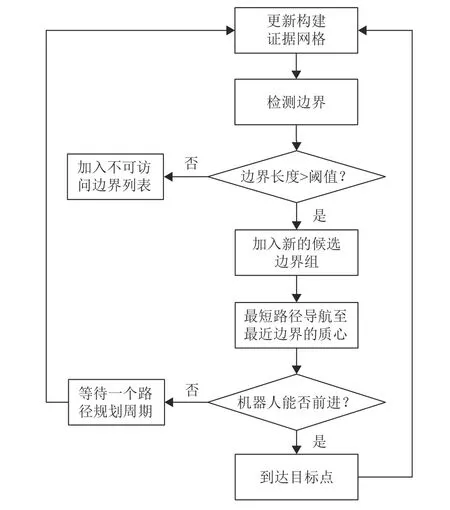
图2 Frontier-based算法流程图Fig.2 Flow chart of the Frontier-based algorithm
运用最小二乘法曲线拟合原理[16],计算 x,y所有数据到拟合曲线的偏差平方和L。
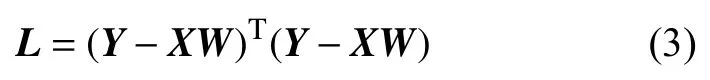
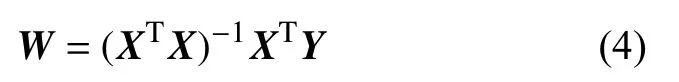
根据 W 得到常量系数a,b,c的值,因而得到根据最小二乘法求得的多项式曲线函数p(x)。
2 Frontier-based算法改进
2.1 基于边界曲线拟合的边界筛选
Frontier-based算法探索建图时将长度大于设定阈值的边界添加入候选边界组,从中选取距离机器人最近的边界作为下一个探索目标区。然而,候选边界组中往往存在边界长度已达到阈值,但是形状曲折细长、周围空间狭窄的边界,如图3所示。当这类边界被选作探索区时,机器人会进入狭窄区域发生碰撞,进而影响构图质量。或者长时间停留原地,无路径到达目标探索点,增加了自主建图时间。
为了提高目标探索点的有效性和可达性,本文算法以Frontier-based算法为基础,以与证据网格表示一致的栅格地图[17]为地图模型,将曲线拟合建模方法应用到候选边界组的筛选方法中,去除不安全边界,筛选安全边界。
2.1.1 局部边界坐标系与全局坐标系的转换
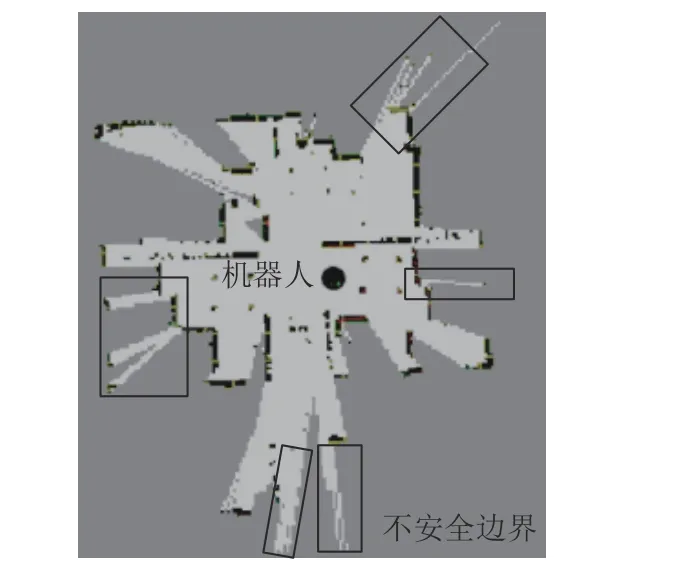
图3 不安全边界示意图Fig.3 Schematic of the insecure boundary
在机器人已建地图中,候选边界组中的边界由多组基于地图全局坐标系的边界点组成,不包含边界的方向信息,所以对边界进行曲线建模时需要针对候选边界组中的边界创建局部边界坐标系。如图4所示,创建局部边界坐标系步骤如下:(1) 坐标系原点:边界质心 O。(2) 坐标系Y 轴:连接边界两端边界点P,Q为一条直线,找到距离该直线最远的边界点 N作为顶点,连接质心与顶点的直线为Y 轴,正方向为质心到顶点的方向。(3) 坐标系 X 轴:坐标系Y轴正向顺时针旋转90°方向为 X 轴正向。
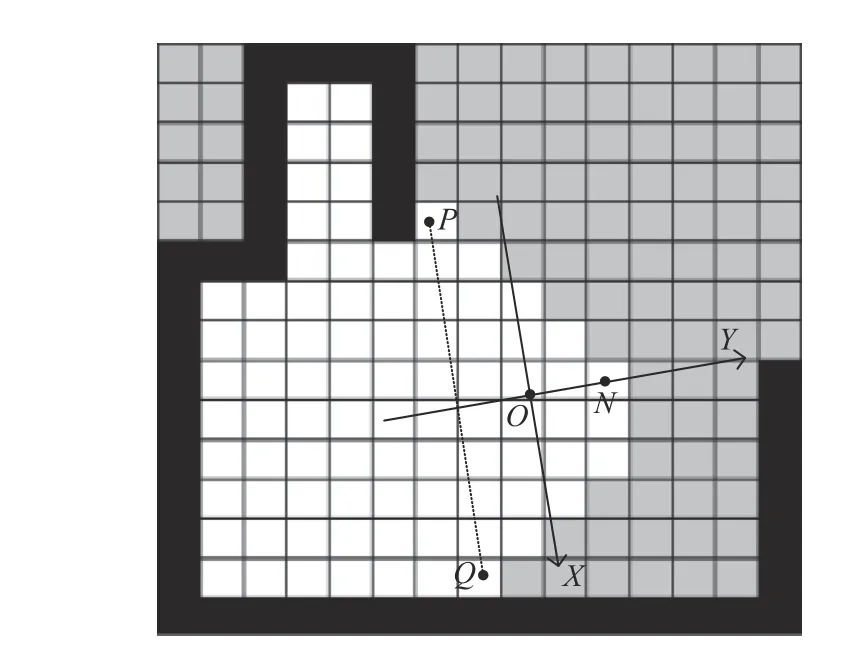
图4 局部边界坐标系Fig.4 Local boundary coordinate system
构建局部边界坐标系后,将边界数值从地图全局坐标系转换到局部边界坐标系下。两坐标系的位置关系如图5所示,O-XgYg表示地图全局坐标系,O′是边界质心,O′-XlYl表示局部边界坐标系, N是边界顶点, S为一条边界中的边界点。
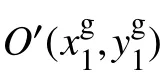
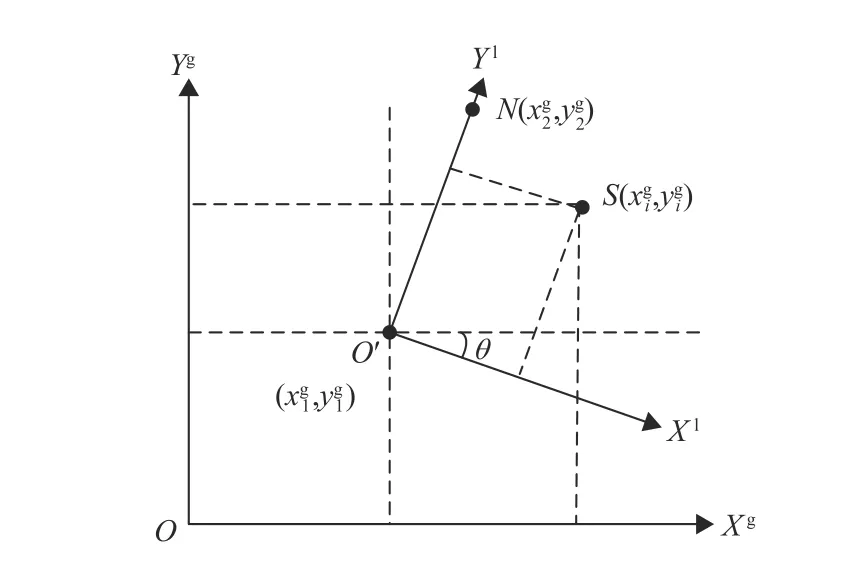
图5 两坐标系转换示意图Fig.5 Schematic of two coordinate systems transformation
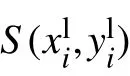
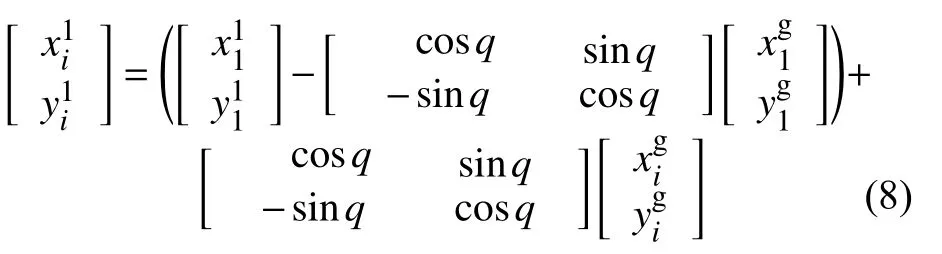
最后,由式(8)可以将边界候选组中的所有边界的边界点从全局坐标系转换到局部边界坐标系下,得到局部边界坐标系下的边界候选组。
2.1.2 边界曲线建模
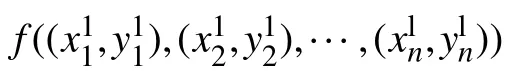
机器人构建地图的边界形状特征多为一元二次曲线图像特征,因此本文算法设边界f拟合曲线多项式pc(x)为
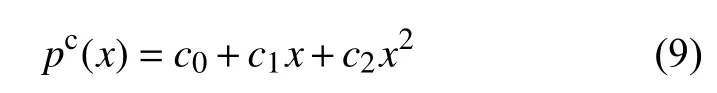
2.1.3 安全边界及目标探索点的选取
根据2.1.2中的方法对候选边界中所有边界进行边界曲线建模,获得所有边界的曲线拟合函数。下一步计算边界的空间宽度,因为边界点分散,不能仅仅通过边界两边的顶点推算。所以本文算法利用边界拟合函数计算边界的空间宽度。如图6所示,曲线A是图中边界的拟合函数pc(x)在坐标系O′-XlYl中的图像, D为边界的空间宽度。当D大于机器人底盘宽度时,将该边界添加入安全边界列表,确定边界空间可以容纳机器人;反之,则添加入不安全边界列表,确定该边界空间狭窄,机器人访问该边界时会发生碰撞。安全边界和目标探索点筛选实现方案如下。
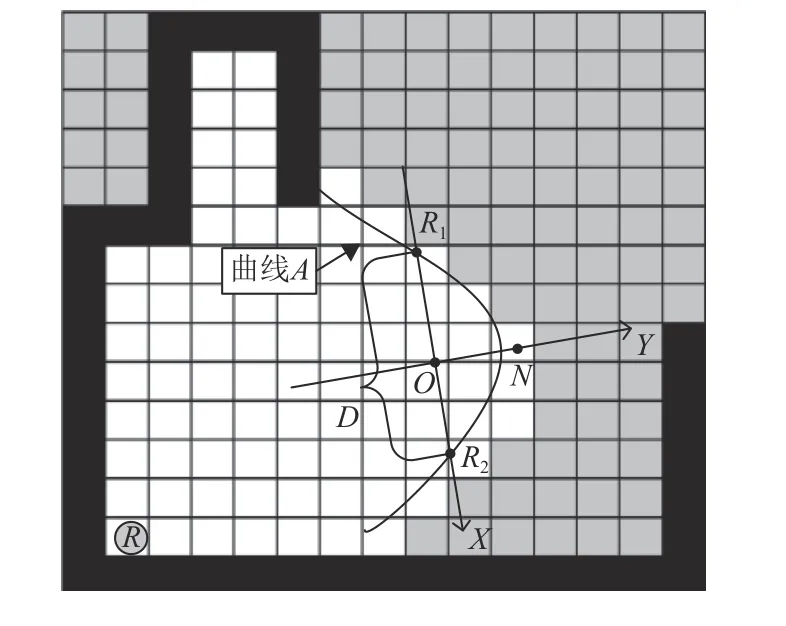
图6 安全边界筛选示意图Fig.6 Schematic of the security boundary screening
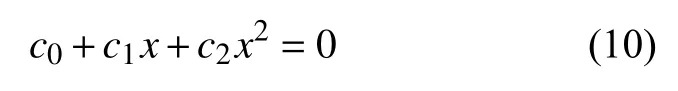
根据求根公式计算式(10)的解,即曲线A的零点R1,R2的横坐标分别为 x1, x2。则边界的空间距离D=|x1- x2|。比较D与机器人底盘宽度2r。

根据以上方法筛选候选边界组中所有边界,在安全边界列表选取与机器人距离最近的边界为探索区,并将该边界的质心作为下一个目标探索点。
2.2 不可达目标探索点规划
Frontier-based算法在获取到目标探索点后,机器人尝试使用路径规划器规划一条最短无障碍路径。若有路径,机器人顺利导航至目标点探索边界,反之,由于室内环境地图复杂,激光雷达为360°发散式扫描,机器人的目标探索边界出现如图7和图8所示的情况:安全边界 f弯曲方向指向地图未知区域,其目标探索点即质心处于机器人未感知的区域。这导致机器人无法规划出一条到达质心位置的路径,只能将该目标边界添加入不可访问边界列表,并原地等待一个路径规划周期(约2 min),再重新确定新的目标探索点,建图效率低。
为了优化上述问题所导致自主探索建图时间长的问题,本文算法将基于滑动窗口的边界邻域规划方法引入Frontier-based算法。
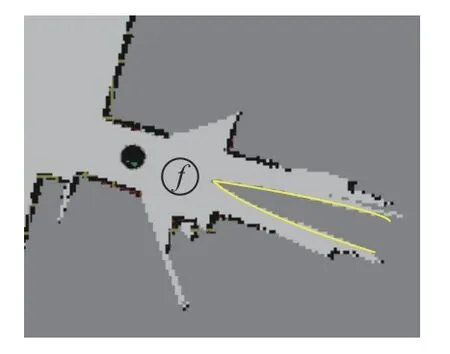
图7 不可达目标探索点Fig.7 Unreachable target exploration point
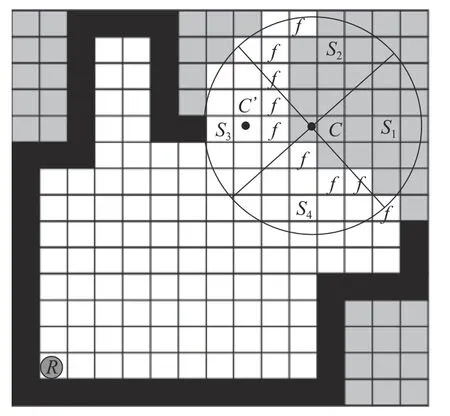
图8 不可达目标探索点邻域规划Fig.8 Neighborhood planning for unreachable target exploration points
基于滑动窗口的边界邻域规划的思想是:对于不可达边界如图8中边界f,采用90°圆形扇面滑动窗口,每次逆时针旋转90°,旋转4次,扫描质心C 的圆形邻域内,寻找可以容纳机器人的可达新目标探索点。从而无需机器人原地等待2 min,并避免机器人放弃对此类边界的探索。
如图8所示,目标边界 f的不可达探索点C 决策出新目标探索点C′。具体算法伪代码为

2.3 CS-frontier算法
本文提出的自主边界探索建图方法 CS-frontier,其自主建图方法流程图如图9所示。
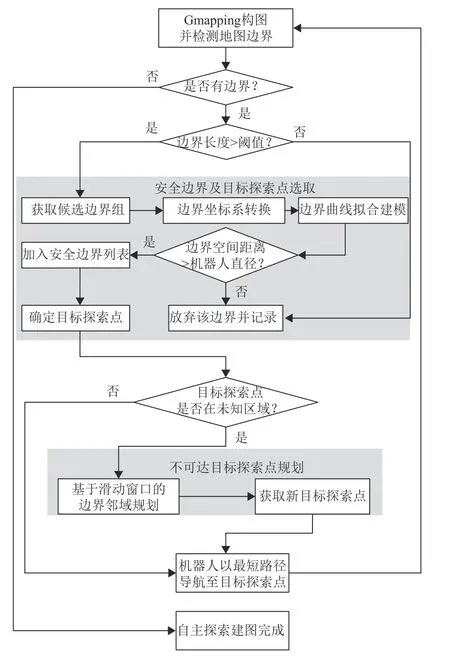
图9 CS-frontier自主建图算法Fig.9 CS-frontier autonomous mapping algorithm
算法步骤如下:
步骤1:收集传感器数据,使用基于SLAM方法的Gmapping(Grid Mapping)算法[19]更新构建环境地图。
步骤2:使用计算机视觉方法检测地图边界。如果存在边界,则添加入边界候选组;反之,执行步骤8。
步骤3:利用边界曲线拟合建模方法筛选候选边界组中边界,将符合边界添加入安全边界列表。
步骤4:选择安全边界列表中与机器人距离最近的边界的质心作为下一步构图的目标探索点。
步骤5:如果目标探索点在地图的空闲区域,则执行步骤7;否则执行步骤6。
步骤6:针对不可达目标探索点,使用基于滑动窗口的边界邻域规划方法推算新的替代点。
步骤7:机器人规划最短无障碍路径导航至目标探索点,然后执行步骤1。
步骤8:自主建图完成。
3 实验
3.1 实验环境
本文的实验分别在两个不同室内场景进行。简单实验场景如图10所示:面积为8 m×9.6 m,障碍物主要是桌子、纸箱、墙壁;复杂实验场景如图11所示:面积为9.5 m×8.0 m,障碍物主要是办公桌、凳子和办公杂物。实验平台如图12所示,包含一台搭载Rplidar A2 360°激光测距雷达的Turtlebot 2机器人和一台搭载英特尔i7-8750H CPU的笔记本电脑。

图10 简单实验环境Fig.10 Simple experimental environment

图11 复杂实验环境Fig.11 Complex experimental environment

图12 Turtlebot 2平台Fig.12 Turtlebot 2 platform
3.2 评价指标
本实验评价指标主要为探索次数:机器人自主建图过程中探索目标点总数;路径长度:机器人自主构建完整地图所移动的路径总长度;自主建图时间:机器人从初始建图到完整建图的时间;地图覆盖率:机器人实时已建地图面积与环境完整地图面积的比例;地图完整度:自主建图完成后,所建地图面积与环境完整地图面积的比例。
3.3 实验数据
本文算法的实验基于机器人操作系统(Robot Operating System,ROS)框架,使用Gmapping算法构建实时栅格地图,使用ROS平台move_base路径规划器规划机器人导航路径。相关实验设置参数如表1所示。
3.4 实验结果与分析
本文在图10、图11所示的室内场景对所提出的算法进行验证。首先机器人在起点处开启Gmapping建图算法,不断以最短路径方式导航至自主探索建图算法决策的目标探索点,最终遍历整个环境。为验证本文算法的有效性,本文进行两项算法对比实验。

表1 实验参数设置Table 1 Experimental parameters setting
3.4.1 对比实验一
CS-frontier算法与Frontier-based算法对比。
(1) 简单环境实验对比。两种探索建图算法在图10环境中进行的实验过程性能对比如图13、图14和表2所示。图13中圆点表示自主建图过程中机器人的目标探索点,箭头线段表示机器人探索建图路径和方向。
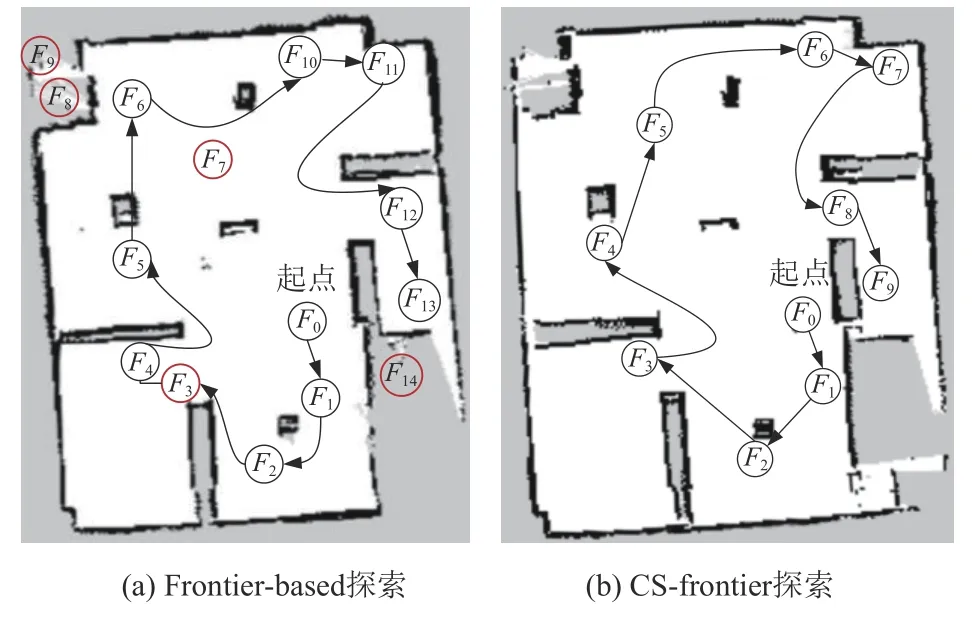
图13 简单环境自主探索建图过程和完成图Fig.13 Mapping process independent exploration and completion map in simple environment

图14 Frontier-based探索中不安全边界Fig.14 Insecure borders in Frontier-based exploration
Frontier-based算法探索次数比CS-frontier算法多5次。通过实验观察,图13(a)中Frontier-based算法探索过程,如图14所示,目标探索点F3,F7位置处于地图的未知区域内,机器人无路径到达,原地旋转规划路径2 min放弃探索;目标探索点F8,F9,F14所属边界长度达到阈值,但是边界空间距离小,为不安全边界,导航过程中机器人发生碰撞,且因空间狭窄到达不了目标位置,等待2 min再决策下一个目标点。
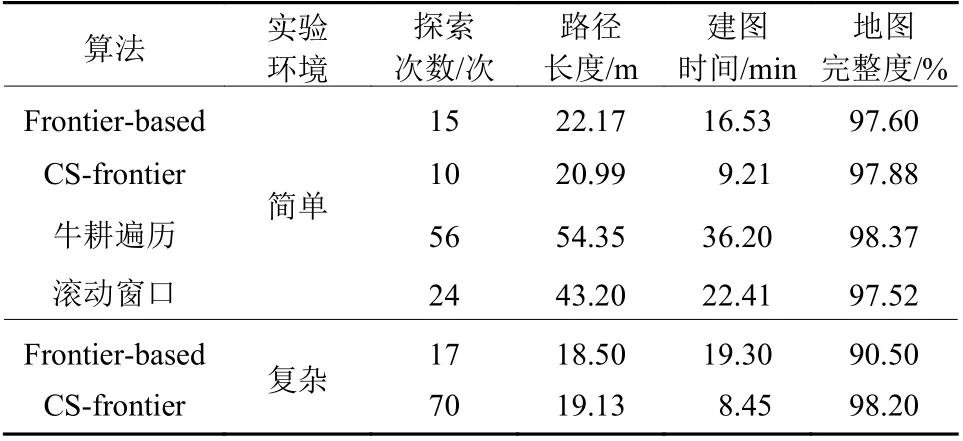
表2 各算法性能对比Table 2 Performance comparison of various algorithms
CS-frontier算法在探索过程中利用边界曲线拟合建模方法筛选掉了不安全边界,并采用滑动窗口边界邻域规划方法对处于未知区域的探索点进行重规划,相对于Frontier-base算法大大缩短了建图时间,自主建图时间仅用9.21 min。
(2) 复杂环境实验对比。两种探索建图算法在图11环境中的实验过程、效果和性能对比如图15和表2所示,Frontier-based算法17次探索中,探索点 F9处于地图未知区域,被放弃探索。还有8个是无路径不安全边界:F1,F2,F3,F4,F6,F7,F10,F15。其中如图15(a)中地图的左上部分,机器人在 F14处使用路径规划器寻找 F15的路径时,由于机器人不断地旋转恢复尝试寻找路径,导致地图角度误差加大,引起建图算法不稳定性,造成已构建的全局地图与局部地图进行匹配时发生偏转,构图发生错误,使得已建地图与实际场景不符,最终地图完整度仅90.5%。
CS-frontier相较于Frontier-based而言,探索次数少且目标探索点均安全有效,虽然探索路径长度相差不大,但是Frontier-based因为对不安全边界的多次路径恢复尝试,导致探索时间增加,也增加了构建地图的不准确性。CS-frontier算法在探索过程中,减少机器人对不安全探索点的探索和机器人碰撞、多次旋转等引起定位误差和地图误差的产生,从而增强了自主建图算法的整体稳定性。如图15(b)所示,CSfrontier算法探索路径平滑,构建的地图误差小,更加准确,地图完整度更高。
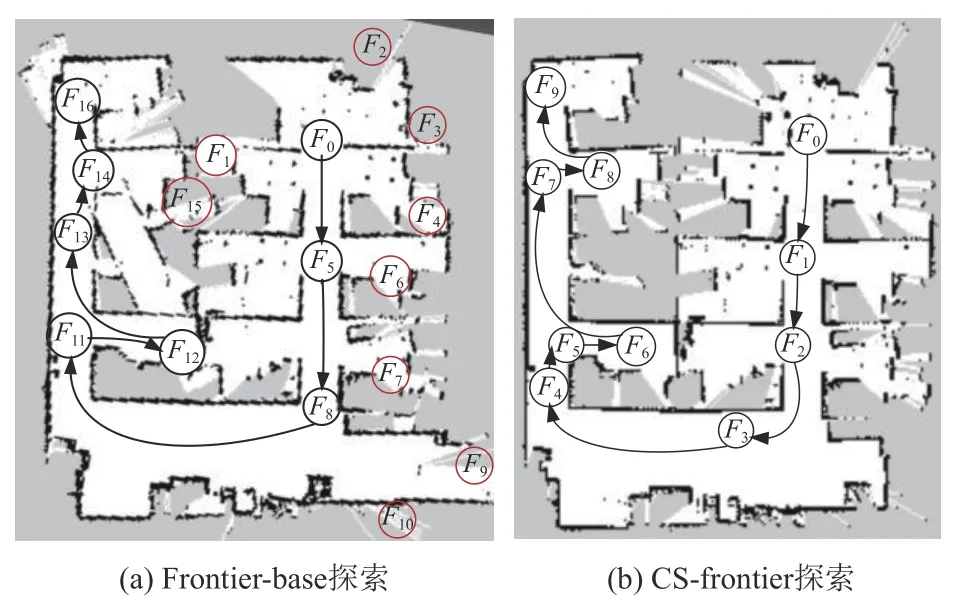
图15 复杂环境自主探索建图过程和完成图Fig.15 Mapping process independent exploration and completion map in complex environments
因此,实验结果表明,在简单环境和复杂环境的不同验证中,本文CS-frontier算法优化了Frontierbased算法中的不安全边界探索和目标探索点无路径问题,本文算法更适应相对复杂的生活、办公环境,自主建图效率高,算法鲁棒性强,整体性能更好、更高效。
3.4.2 对比实验二
CS-frontier算法与以下两种自主建图算法在如图10环境中进行实验对比:牛耕式全覆盖遍历算法[20],该算法自主建图按照左下右上的路径方式遍历整个环境;基于滚动窗口的机器人自主构图算法[6],使用滚动窗口的方式让机器人滚动探测地图。对比结果如表2、图16所示。
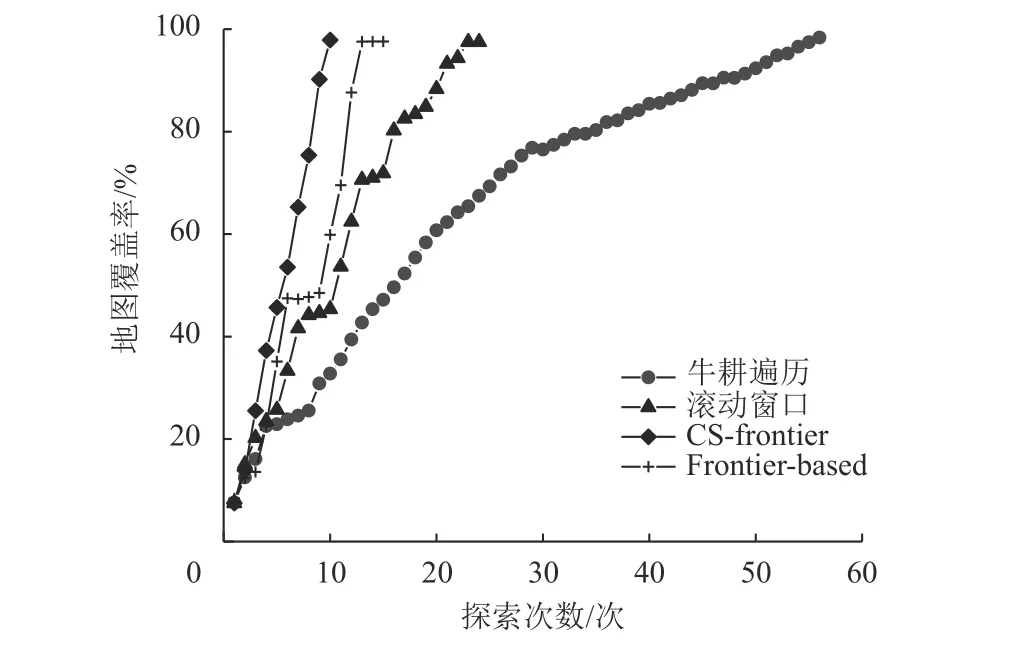
图16 地图覆盖率对比图Fig.16 Comparison of the map coverage
从探索次数看,CS-frontier算法探索次数最少,牛耕遍历算法最多,从路径长度和建图时间来看,CS-frontier算法的总路径最短,自主建图时间仅用9.21 min,就达到较高的地图完整度。从地图覆盖率看,如图16所示,随着探索次数增加,牛耕遍历法上升速度最慢,滑动窗口算法因为窗口滑动地图重复多,覆盖率增加较慢,Frontier-based算法在无效探索点处影响了覆盖率的增加,CS-frontier算法上升速度最快,地图重复率最低。
实验表明本文提出的CS-frontier算法相比传统的自主探索建图算法,可选择更少的探索点,以更高的探索效率和更平滑的路径完成自主探索建图。
4 结论
为了更好地实现移动机器人自主构建未知环境的栅格地图模型,提高机器人自主性和智能化水平,本文提出 CS-frontier自主边界探索建图方法。该方法针对在未知环境下,机器人如何自主探索未知区域进行构图,并克服边界狭窄探索区域影响构图完整性的问题,一方面,根据已构地图边界的曲线特征,采用边界曲线建模方法,选取安全边界,再选择与机器人最短距离的安全边界探索点作为下一个探索区;另一方面,通过基于滑动窗口的边界邻域规划算法确定处于未知区域目标点的探索,提高了自主建图的通用性。通过在实际室内复杂场地多次重复对比实验表明,本文方法无论是与目前经典的Frontierbased边界探索算法,还是传统牛耕全覆盖遍历算法及基于滚动窗口的机器人自主构图算法相比,都有更高的探索效率和通用性。
然而在机器人建图过程中,里程计、电机旋转角度等累计误差都会引起建图算法中局部地图与全局地图匹配的误差,影响机器人构建地图的准确性。所以在研究提高机器人探索未知环境构图的自主性的同时,考虑建图算法的稳定性和精确性是下一步研究工作的内容。

