样本不均衡条件下设备健康度评估方法
赵丽琴,刘 昶,邓丞君
(成都大学 信息科学与工程学院,成都 610106)
0 引言
健康度是设备量化的健康程度,是一种设备健康状态的定量评估,可以更准确的反映设备健康状态。随着大型机电设备系统集成化、信息化程度的提高,其故障诊断与后勤保障的难度增大。为保障这些系统连续稳定的运行,不影响任务的正常执行,减少资源浪费,提高设备保养和维修效率,需随时掌握设备的健康度,并根据系统健康度做出适当的维修维护决策,提高其工作效能。
根据文献,目前对复杂系统健康度的评估,大部分都是基于向量距离的计算,也有部分是基于模糊评判或者信息熵方法。一般常规的方法包括:综合权重法、模糊隶属度、层次分析、灰色关联、高斯模型等。如文献[1-4]就运用了综合权重和模糊评价法对设备的健康度进行了评估。文献[5]利用模糊测度和模糊积分来计算配电网关键设备的健康度。文献[6-7] 利用回归算法预测健康度,取得了不错效果。也有学者用灰色关联法计算采集向量和虚拟向量的关联度,得到健康度,对设备进行健康度评估[8-9]。文献[10]分两级计算设备健康度,在部件级计算了带加权的距离,然后通过动态权重的模糊层次法计算系统级健康度。但这些方法都需要良好的先验知识来确定权重及模糊函数等信息,且不适应大量采样数据场合。
随着大数据分析技术的出现,利用机器学习方法进行健康度评估的研究越来越多。例如为了对风洞设备进行健康状态评估,文献[11]利用深度学习LSTM算法,先降维,再计算向量距离得到健康度。利用传统机器学习技术如支持向量机(SVM)算法来进行健康状态评估的研究也得到广泛重视。比如有研究采用SVM算法对高铁动车的轴承进行健康评估[12];还有研究利用SVM算法对舰船的推进系统进行健康管理[13]。相对于深度学习算法,SVM算法占用资源少,训练样本要求不多,而准确度相差不大[14],因此成为设备健康状态评估的主流研究方向。SVM方法是以多分类为框架,SVM通过对设备正常数据和异常数据进行学习构建分类器进行测试。但在实际测量中,容易获得大量的正常样本,而异常样本不易获得,就会造成严重的数据不平衡问题。如果异常样本匮乏,则SVM不能很好地发挥作用,对于异常情况的分类效果就不甚理想[15]。
鉴于大多数设备具备较多的正常数据,缺乏或者只有少量异常状态数据,SVDD作为一种单分类学习方法,成为一种评价健康度较好的备选方法。如文献[16]采用主成分分析法、SVDD算法和马氏距离等方法,计算设备的实时健康度。文献[17]将模糊理论与SVDD算法相结合,提出基于模糊SVDD的电子装备状态评估模型。但该方法未考虑不同属性的权重,适用于样本权重均衡的场合。郑州大学的李凌均等[18]将支持向量数据描述用于机械设备状态评估研究,仅仅依靠正常运行时的数据信号,而不需要故障数据,就可以监测机器的运行状态,对早期故障诊断提供很好的帮助。
基于SVDD的单类学习方法在机械设备异常检测、设备故障预警,图像异常检测等领域逐渐得到广泛应用,但在设备健康状态评估方面应用甚少且准确性不高。本文以采集样本不均衡的设备为评估研究对象,提出了基于动态权重的SVDD设备健康度评估方法。该方法首先采用SVDD算法训练正常健康状态的样本得到一个超球面,然后利用少量各种健康度的标记样本计算其到超球面距离,再采用二项式回归学习算法得到健康度计算的拟合曲线。为了提高评估的准确性,本方法特别考虑了设备采样参数值在偏离最佳值越大时,健康度越差的事实,提出了基于指数函数的动态权重算法。将该算法与前面方法结合可显著提高准确性。最后以某型雷达发射机为例进行测试验证。实验结果表明,该方法对设备健康度准确评估具有不错实用价值。
1 SVDD模型
作为一种典型的单分类器,采用SVDD模型,对健康数据进行训练后就可以对健康状态和非健康状态进行分类,适合缺乏全面样本的场合。
假定健康样本数据为集合{xi},xi∈Rd,i=1,…,N,训练SVDD模型的目标是找到一个最小体积的超球体,使所有向量xi都包含在该球体内。用圆心a和半径R来表示这个超球体。为了减少奇异点的影响,引入松弛变量ξi,问题转化为求解下面的二次规划问题[14]:
(1)
式中,C为惩罚系数,ξi≥0(i=1,…,N),‖φ(xi)-a‖2为点φ(xi)到球心a的距离。通过建立拉格朗日函数,并引入核函数κ(xi,xj)=φ(xi).φ(xj)代替内积运算,将上述二次规划问题转化为如下对偶问题:
(2)

解上述不等式,得到球心:
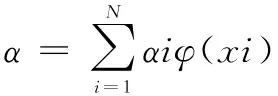
(3)
取特征空间内任一支持向量φ(xk),可得半径:

(4)
相应地,一个样本点z到球心a欧式距离d为:
(5)
2 融合动态权重归一化算法
2.1 基于指数函数的动态权重算法
通常一个设备有多个与健康状态相关的参数,不同参数对设备健康状态的影响不同。采用权重法是一种惯常做法。在工作中发现,一个参数对健康状态的影响并不是一成不变的,随着其参数值大小变化而变化。比如某个参数平时在正常范围内,对健康状态影响不大。但是随着参数值偏离正常值越多,对健康状态的影响就越大。根据长期观察和实验验证,参数值变化对健康状态的影响程度比较贴近指数函数。因此,对于参数i的动态权重指数,可用如下指数函数表示:
(6)

在公式(6)中gi是归一化之后的参数检测值。ψi是参数i的动态权重的指数函数参数,要求ψi>1,其具体值根据参数在报警区域对整个设备的健康度影响程度而定。影响越大,可设定ψi的值越大。不同采集参数具有不同的ψ值,说明参数值增加时,对整个健康度的影响程度。xi是采集参数i的值,ηi是参数i最佳值。boundi是其边界阈值。很明显,当采集参数值超过边界值时,会快速增加,凸显该参数对整个健康状态的影响显著增强。
参数i的综合权重指数w’i是动态权重指数wid和静态权重指数wis之和,如公式(7)。
(7)
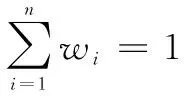
(8)
2.2 基于权重因子的数据归一化算法
为了得到含有权重因子的待处理数据,在数据进行归一化处理时,需要融合权重因子的影响,这样就更好地反映了各个参数对健康度的影响。含有权重的归一化采集数据值为:
(9)
在公式(9)中,xi是采集参数i的数据值,wi是其对应的权重因子。μi则是该参数最佳值,δi是其标准差,考虑计算标准差的特殊性,可采用迭代算法[19]。这样计算的结果代替原始采集数据xi用于SVDD建模及后续SVDD距离计算,可以很好地体现某些恶化参数对健康度的影响。
2.3 多项式回归拟合算法
SVDD模型超球面反映了健康数据的范围。对每个采集数据向量z,可以计算其到超球面圆心的距离d,然后根据这个距离大小可以得到量化的健康状态,即健康度。通常d越大表示数据所代表的健康状态越差,如图1所示。
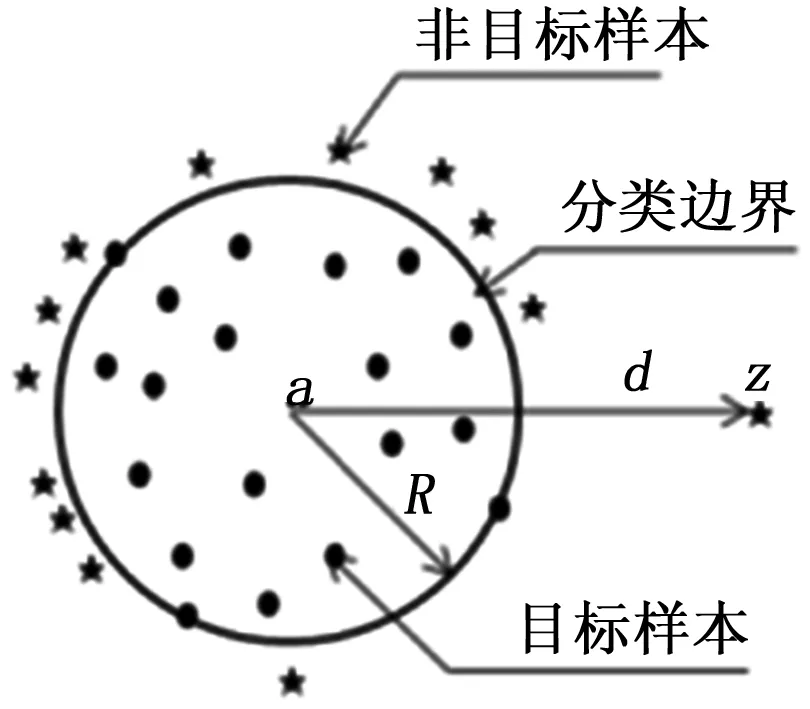
图1 不同样本与SVDD超球体位置关系
通过拟合运算可以从距离d得到健康度。要进行拟合运算需要有各种健康状态的样本数据。但在样本不均衡情况下,很难有全面的样本数据。通常对缺乏的数据样本通过人工经验进行构造。训练样本的距离d和健康度E之间属于一种函数关系,根据设备健康度的变化特点,采用二项式回归模型具有较好的拟合效果。二项式回归的本质是通过学习,构造一条二项式曲线:
Eθ(d)=θ0+θ1d+θ2d2
(10)
二项式曲线应该尽可能拟合所有用于训练样本的距离d及其评估健康度E。当未来的采集数据计算出距离d后,可以很快根据曲线函数得到对应的健康度Eθ。
2.4 数据预处理算法
1)主成分分析法:
为了降低处理强度,在采集数据较多时,需要进行降维处理。即在尽可能保留原始数据特征的同时,尽可能降低处理数据的维度。本方法采用了PCA主成分分析法(Principal Component Analysis)来进行降维处理。它是一种常用的高维数据降维方法。其基本处理流程如图2所示。

图2 PCA降维处理方法流程
图2是M条N维数据进行降维处理后,得到k维数据的处理过程。由于其处理过程比较简单固定,在此不做过多分析。
2)异常值剔除算法:
异常值一般是由于采集器件出现漂移或者故障出现的,对健康状态的评估具有错误的指示,需要剔除。基本思想是规定一个置信限度,凡是误差超过该限度的值认为是异常值。本文采用一阶差分法,即用两个测量值来预估新的测量值,然后与实际测量值进行比较,如果大于设定的阈值,则认为是异常值需要剔除。令xn是采集值,则:
x′n=xn-1+(xn-1-xn-2)
(11)
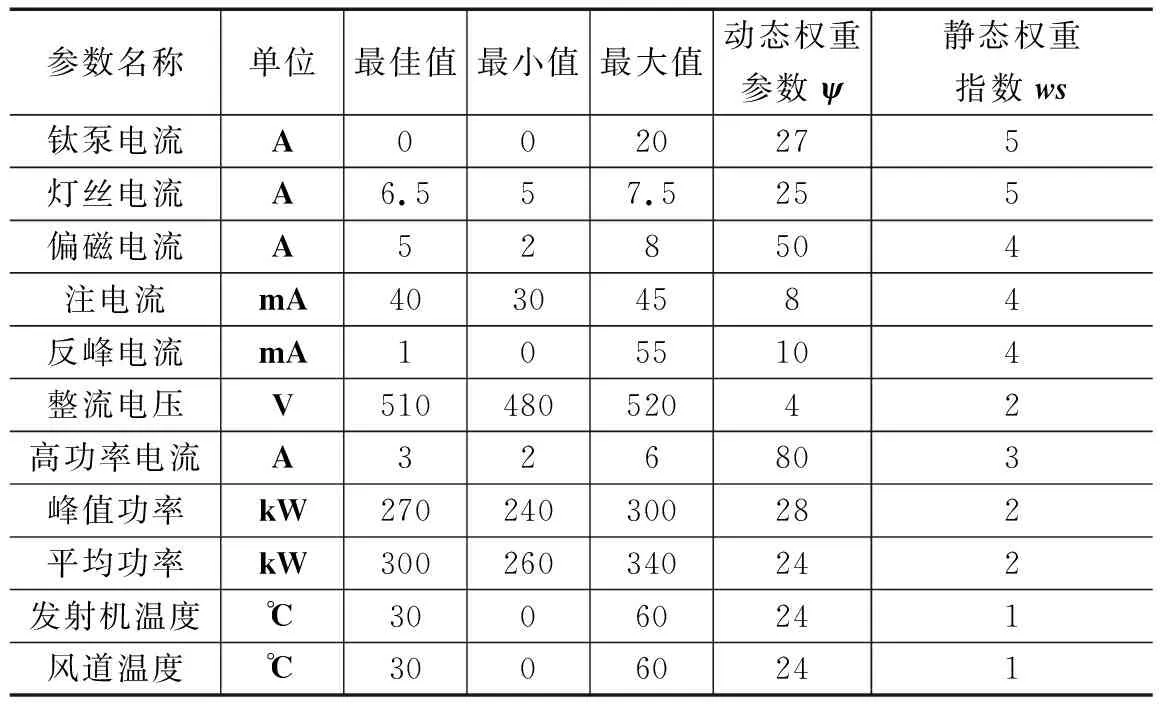
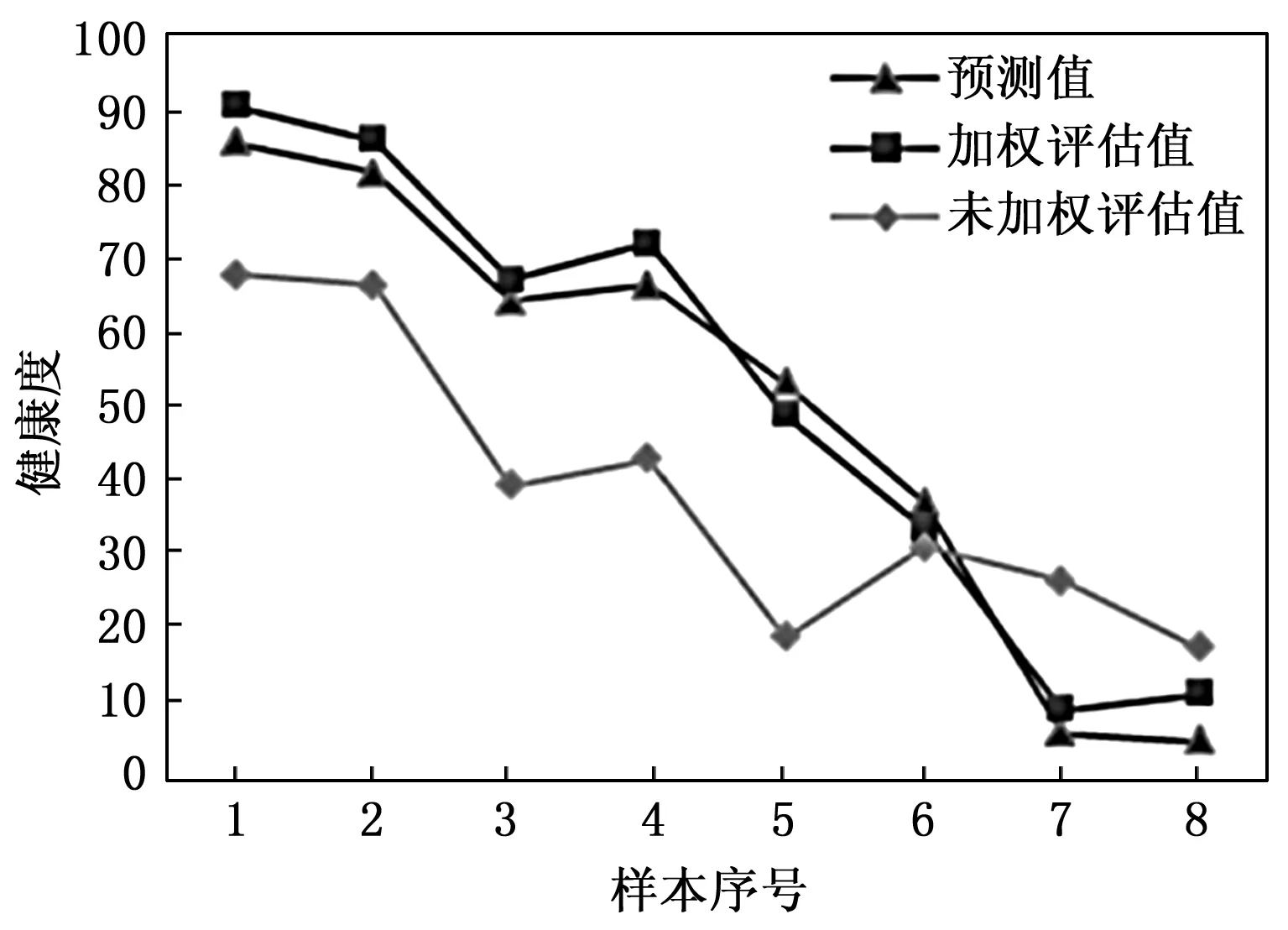
|xn-x′n| (12) 公式(11)计算出参数的当前估计值x’n,在公式(12)中与真实的参数进行比较。w为设定的阈值,与参数的变化幅度有关。 3)参数平滑处理方法: 设备检测参数由于设备的原因,免不了有噪声影响。采用平滑处理可以减少噪声影响,还可以表现参数数据的周期趋势。采用指数加权平均算法,运算量少,且具有不错的效果。 vt=βvt-1+(1-β)xt (13) 其中:vt是要代替的估计值,即t时刻的指数加权平均值。xt是t时刻采集的参数值;β是一个权重参数(0 <β< 1 )。β越小,噪声越多,虽然可以很快适应参数的变化,但是容易出现异常值;β越大,得到的结果越平滑,但是对参数变化的适应慢。一般需要根据参数的实际情况进行调节,得到最佳效果。一般令β= 0.9。 综合以上算法,可以总结出基于SVDD的健康度评估过程如图3所示。整个过程分为两阶段进行: 图3 基于SVDD的健康度评估算法 1)在学习阶段,主要针对样本训练集进行处理。鉴于样本数据已经经过选择,一般不需要再进行预处理。这里主要根据样本向量中的参数值计算其动态权重指数,得到各个参数的权重因子,然后利用公式(9)计算含权重因子的归一化数据。如果样本处于健康状态,则进行SVDD超球面训练得到SVDD模型。如果是非健康数据,则利用SVDD模型计算到其到超球面圆心距离d,根据其评估的健康度E进行二项式回归学习,得到计算健康度的二项式回归模型。 2)在检测阶段,主要针对测试和检测集。首先进行数据预处理和权重因子计算,得到包含权重因子的归一化数据,然后利用SVDD模型计算到超球面圆心距离d,接着利用前面学习得到的二项式回归模型计算健康度,从而得到评估结果。 无论在训练阶段还是检测阶段,都利用了主成分分析的结果来选择样本向量参数,降低分析向量维度,提高分析效率。 为了验证前述方法的正确性,利用某型雷达发射机作为实际例子进行评估分析。雷达发射机是雷达最重要的关键子系统,也是容易出现故障的部分,是重点健康管理监控设备。 1)采集数据分析,构建专家知识表: 雷达发射机的作用是在定时信号的激励下,产生大功率的射频信号。其状态监控参数较多,主要包括电磁信号参数、机械性能参数、电力参数及热参数等。为了对本文所提方法进行评估,针对某型气象雷达的发射机系统进行了实例评估。该雷达发射机采集了将近二十多个数据,但并不是所有数据都与健康状态密切有关。利用PCA算法及专家评估后,将与健康状态有主要影响的参数分辨出来。最后选择了11个与健康状态密切相关的参数作为处理数据集,得到的专家知识表如表1所示。表中包括各个参数的最佳值、最大值、最小值边界,以及静态权重ws、动态权重参数φ等。需要根据采集值和最佳值的大小来决定bound值是选择最大值还是最小值。雷达专家在长期维修过程中,对这些参数的含义具有非常深刻的理解,因此填写表1的信息并不困难。虽然不是特别准确,但对用于验证本方法已经具有足够的准确性。 表1 主要监测参数基本信息表 2)构建样本数据集: 在实际采集的雷达发射机监测数据中,共选取了3 000组数据作为训练和测试样本。其中2 900组数据是健康数据样本用来训练SVDD模型,另外100组数据是各种健康状态下的数据样本。选择了其中92组用于二项式回归学习建模,另外8组具有各种健康状态的样本作为测试集。由于非健康数据样本积累较少,大部分非健康数据样本利用了平时故障模型,并根据专家经验评估其健康度,作为有标记样本。在整个处理过程中,所有样本数据都需要计算动态权重,最后按照公式(9)进行加权的归一化计算,便于后续分析。 3)利用SVDD模型进行训练得到超球面: 首先利用其中的2 900组健康数据样本训练SVDD模型。为了比较不同情况下训练的结果,分别用两种情况下的数据样本进行了训练,即①原始数据;②利用权重因子加权的数据。两种情况下得到的超球面数据如表2所示。 表2 不同处理情况下的超球面数据 由于是11维的数据向量,其圆心也是由11个数据构成的数组。很明显,在同样的样本下,加权处理后的数据超球面半径小很多,证明数据收敛程度更好。 4)利用二项式回归训练方法建立健康度拟合曲线: 使用了92组数据进行二项式回归训练。每个健康状态有20多个样本,得到样本到超球面圆心的距离与健康度的映射关系。为了对比,也是针对SVDD的两种情况进行分别训练,结果如表3所示。 表3 二项式回归拟合结果 5)结果分析: 8个用于测试的样本中,每个健康状态有两个样本。与前面一样,也是分别针对两种数据处理情况,进行健康度评估测试。测试结果对比曲线如图4所示。其中的标定健康度是根据专家经验人工标定的结果。 图4 测试样本的结果分析 测试表明,经过加权处理之后评估健康度最接近人工标定的健康度,在各种不同健康状态下的测试结果都比较稳定,具有最佳效果。而没有加权处理的结果偏离比较大。虽然整体趋势也比较一致,但在很多情况下,并不嫩准确地反应设备应有的健康状态。 针对设备在进行健康管理过程中存在的样本不均衡性,本文利用了SVDD模型超球面的特点,通过权重因子融合了采集参数值变化对健康状态的影响。结合二项式回归拟合算法,提出了一种适用于采样不均衡条件下的设备健康度评估方法。该方法有效解决了实际工作中由于样本缺乏或样本不均衡情况下设备健康度评价的难题。特别是利用指数函数动态调整各参数在取值不同情况下对健康状态的影响,反映了各个参数对健康状态影响的动态变化,对健康度的准确评估具有重要意义。通过对某型雷达发射机的实际评估和分析,该方法对于准确评估设备的健康度适应性好,具有不错的实用价值。2.5 健康度评估方法

3 健康度实例评估与分析


4 结束语

