基于快速终端滑模面的两旋翼飞行器有限时间姿态控制
沈林武,陈 强,陶玫玲,何熊熊
(1.浙江工业大学 信息工程学院,杭州 3100232.浙江机电职业技术学院 电气电子技术系,杭州 310053)
0 引言
无人机由于其多功能性、机动性和实用性,引起了国内外学者的极大重视。旋翼飞行器作为无人机的一种常见类型,具有体积小,结构简单和机动性强等优点[1],通常用于某些危险的环境中,包括搜索、营救、区域制图和监视等[2-3]。当前,旋翼飞行器的姿态控制逐步成为无人机控制研究的热点问题[4-8]。为保证四旋翼倾转飞行器的姿态稳定,文献[9]设计比例积分微分(proportion-integration-differentiation,PID)控制器,融合自适应控制算法,实现PID参数自整定,经仿真实验表明该控制器的稳态性能和跟踪性能良好。文献[10]利用前馈控制和线性化技术,设计四旋翼无人机控制算法,并基于线性二次调节器设计姿态控制器,通过反馈调节矩阵增益,改善控制器性能,根据时延、上升时间、超调等参数验证了其优越性能。文献[11]针对三旋翼飞行器尾部舵机发生堵塞故障的情况下,基于反步法和终端滑模控制技术,提出一种鲁棒容错控制方法,经李雅普诺夫方法证明姿态跟踪误差渐近收敛,且经实验验证对姿态控制有较好的效果。文献[12]利用反步法技术和常规滑模设计控制器,常规滑模控制器保证姿态角快速收敛的能力,反步法技术应用于位置跟踪,最终获得四旋翼飞行器位姿的快速收敛,模拟仿真实验验证所设计控制器的有效性。然而,上述控制方法仅能实现姿态的渐近收敛。
与上述方法相比,有限时间控制能实现系统状态变量的有限时间收敛。文献[13]针对刚性航天器带有控制输入饱和的输出反馈姿态控制,基于四元数方法建立系统数学模型,结合有限时间观测器,设计有限时间控制律,保证系统姿态有限时间收敛于平衡点。文献[14]利用分段函数设计一种终端滑模控制策略,结合自适应技术,保证刚性飞行器的有限时间姿态收敛,且更鲁棒、收敛速度更快、控制精度更高等性能,仿真结果表明了该控制策略的有效性。文献[15]针对存在转动惯量有界、未知外部干扰的情况,基于四元数建立刚性飞行器动力学模型,设计有限时间全阶滑模连续控制器,保证系统轨迹有限时间收敛于平衡点,所提控制器有效性经仿真验证。
基于上述讨论,本文针对两旋翼飞行器提出一种基于快速终端滑模面的有限时间自适应姿态控制方法,保证两旋翼飞行器姿态角跟踪误差的有限时间收敛。通过设计分段函数避免控制律和滑模变量求导产生的奇异值问题,同时设计用于估计系统模型不确定上界和未知外部干扰的自适应更新律,并无需提前了解系统的先验知识。最后,在两旋翼飞行器平台上验证所提控制方法的有效性。
1 系统描述及预备知识
图1为两旋翼飞行器测试台示意图,由机械和电子两部分组成。机械部分包含底板、支架、平衡杆和轴承对组件;电子部分由陀螺仪模块、控制单元、电子调速器和无刷直流电机组件构成,其中两个无刷直流电机的桨叶分别为正桨叶和反桨叶,以抵消两个电机不同旋转方向的转矩。
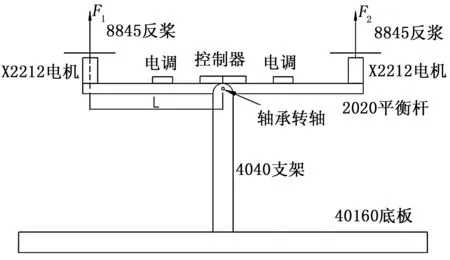
图1 两旋翼飞行器测试台示意图
两旋翼飞行器平衡杆可认为是刚体,根据杠杆原理,其桨叶产生的升力矩Mb为:
Mb=(F1-F2)L=ku,
(1)
式中,F1、F2为桨叶产生的升力,L是电机轴中心线到转轴中心线的垂直距离,k为正系数,u∈R为电机电子调速器控制输入。
基于刚体定轴转动的动力学方程分析,两旋翼飞行器动力学模型的表达式为:
(2)
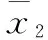
(3)
假设1:Mf和Md有界,即f(x1,x2)和d(t,x1,x2)有界,存在常数F>0和D>0,保证|f(x1,x2)|≤F和|d(t,x1,x2)|≤D成立。

收敛时间上界Tr满足
(4)
2 快速终端滑模控制器
2.1 滑模面设计
设计快速终端滑模面为:
(5)
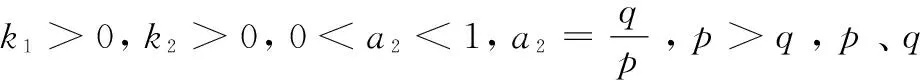
根据两旋翼飞行器控制系统(3)可得:
(6)

对式(5)求导,得:
(7)
滑模变量s一旦到达滑模面s=0之后, 式(4)表示为:
(8)
选取李雅普诺夫函数:
(9)
对其求导,得:
(10)
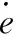
(11)
2.2 控制律设计
设计有限时间自适应控制律u为:
(12)
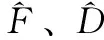
设计自适应更新律为:
(13)
(14)
式中,p1>0,p2>0,c1>0,c2>0。
3 定性证明
定理1:针对两旋翼飞行器系统式(3),设计快速终端滑模面式(5),控制律式(12),自适应更新律式(13)和式(14),则:
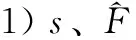
证明:(1)构造李雅普诺夫函数:
(15)
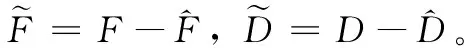
对式(15)求导,可得:
(16)
把控制律式(12)代入式(16),得:
(17)
把自适应更新律式(13)和式(14)代入式(17),得:
(18)
根据杨不等式,以下不等式成立,
(19)
(20)

把式(19)和式(20)代入式(18),得:
-η0V2+υ1
(21)
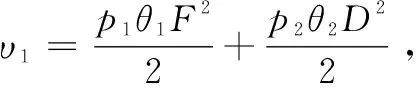
(2)构造李雅普诺夫函数:
(22)
对式(22)求导,可得:
(23)
把控制律式(12)代入式(23),得:
(24)
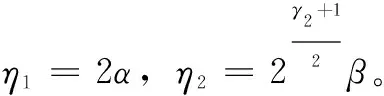
根据引理1,滑模变量s在趋近模态时有限时间收敛到平衡点附近邻域Δs:
(25)
且收敛时间上界Tr为:
(26)
把式(25)代入滑模面式(5),得:
(27)
式中,|ε|≤Δs。
由式(27)可知,姿态角误差e收敛至以下邻域:
(28)
(29)
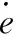
T≤Tr+Ts=
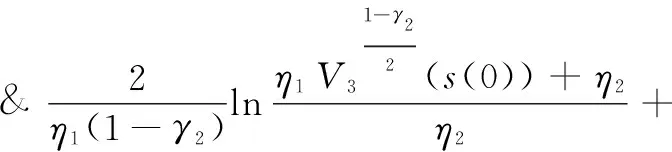
(30)
注:根据式(30),系统状态变量的收敛时间与系统初始值条件相关,如滑模面初始值s(0)、姿态角误差初始值e(0),且其它可设计参数也能影响系统收敛时间上界,如k1、k2、a2、γ2、η1、η2等。如减少γ2、a2,可缩短系统状态变量的收敛时间,但是过小的γ2、a2,等同于控制器获得过高的增益,导致系统的大幅度颤振、甚至不稳定。为了获得系统收敛时间与稳定性之间的平衡,选择合理的控制参数也是设计工作中的一项重要工作,证毕。
4 实验结果与分析
4.1 实验平台描述
两旋翼飞行器控制系统如图2所示,该系统由飞行器测试台、上位机控制台以及辅助直流电源组成。
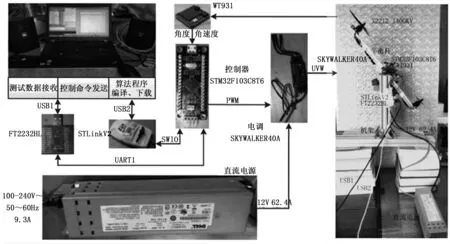
图2 两旋翼飞行器控制系统
两旋翼飞行器测试台有两台无刷直流电机(X2212,中山市朗宇模型有限公司);两台电子调速器(SKYWALKER 40A,深圳市好盈科技有限公司),电子调速器用于控制无刷直流电机的转速;一个陀螺仪模块(WT931,深圳维特智能科技有限公司),用于获取两旋翼飞行器测试台平衡杆的姿态角和角速度;一个用于执行控制方法的控制单元(STM32F103C8T6,意法半导体有限公司)和必要的机械支撑铝合金结构件。两旋翼飞行器电子线路硬件连接图如图3所示。
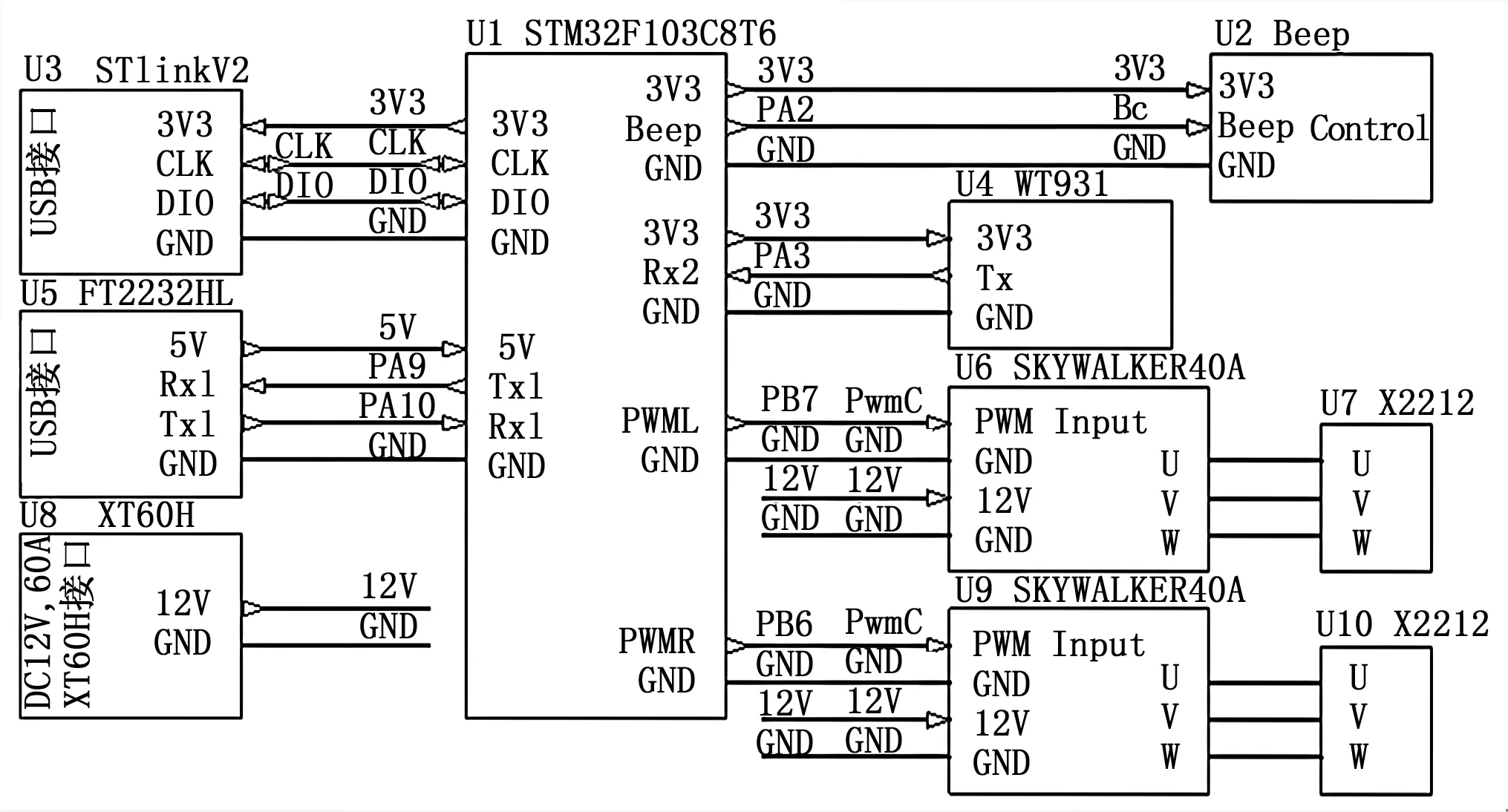
图3 两旋翼飞行器电子线路硬件连接图
上位机控制台为一台工作站(W520,联想控股股份有限公司)。其中通用串行总线(universal serial bus,USB)接口1用于连接飞行器测试台数据接口(FT2232HL,FTDI Chip),实现实验数据的采集、控制飞行器测试台的启停;USB2接口通过调试器(STlinkV2,意法半导体有限公司),与飞行器测试台的控制单元连接,实现控制程序的编译和加载。上位机控制台通过中间文件获取实验数据,实现实验数据的显示、分析和处理。
在实验中,仅使用两旋翼飞行器测试台平衡杆的俯仰轴,陀螺仪模块提供相应的姿态角和角速度信息,其中姿态角的动态精度可达0.1°,姿态角速度测量范围±1 000°/s,采样周期为6 ms,满足后续的闭环信号控制要求。
两旋翼飞行器测试台的指标参数:
1)平衡杆实验角度范围为±60°。
2)陀螺仪模块与控制单元通信速率为921 600 bps,本测试台仅使用俯仰姿态角和角速度。
3)控制算法输出控制量u为±1 500,待机电门控制量u0为3 000,控制单元最终输出控制量u1最大输出值为10 000,为实验安全考虑,限幅值为4 500,则控制量u1范围为500~ 4 500。
4)USB1转通用异步收发传输器(univer sal asynchronous receiver/transmitter,UART)接口1的通信速率为921 600 bps。
5)下载调试器STlinkV2的单总线接口(single wire,SW)运行频率为1.8 MHz。
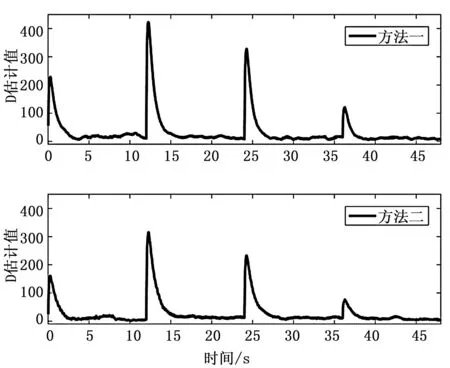
4.2 实验方法对比
为验证所提控制方法的可行性和优越性,提出两种控制方法在两旋翼飞行器测试台进行实验比较。方法一为本文所设计的基于快速终端滑模面的有限时间姿态控制方法,方法二为文献[18]的线性滑模控制方法。为保证公平比较,两种控制方法相应的系统控制参数设置一致。
方法一的滑模面为式(5),控制律为式(12),自适应更新律为式(13)~(14)。
方法二的滑模面为:
(31)
式中,k1>0。
¨控制律设计为:
(32)

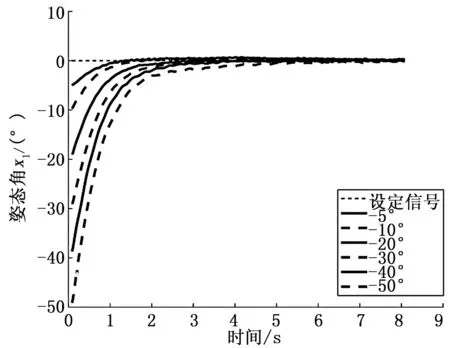
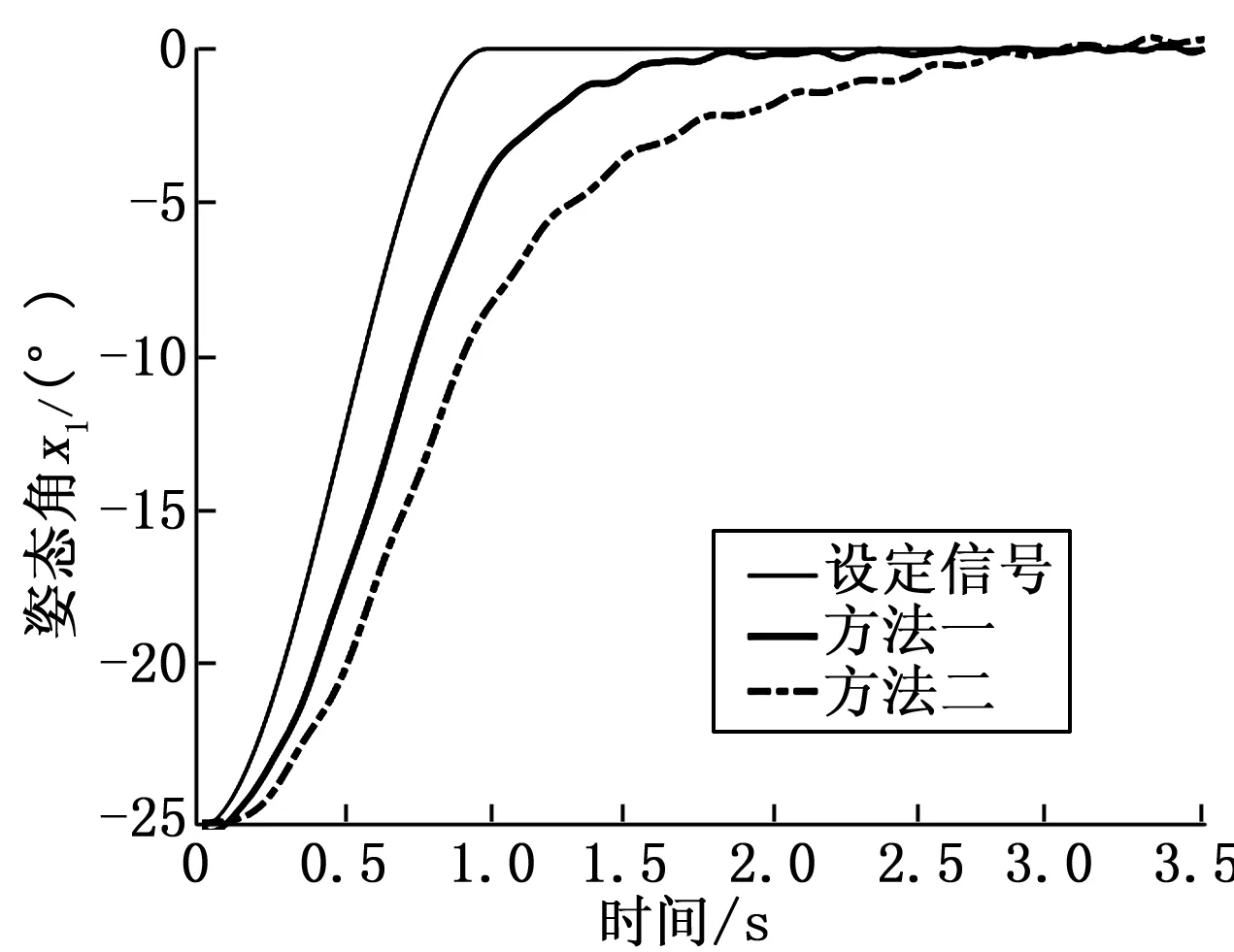
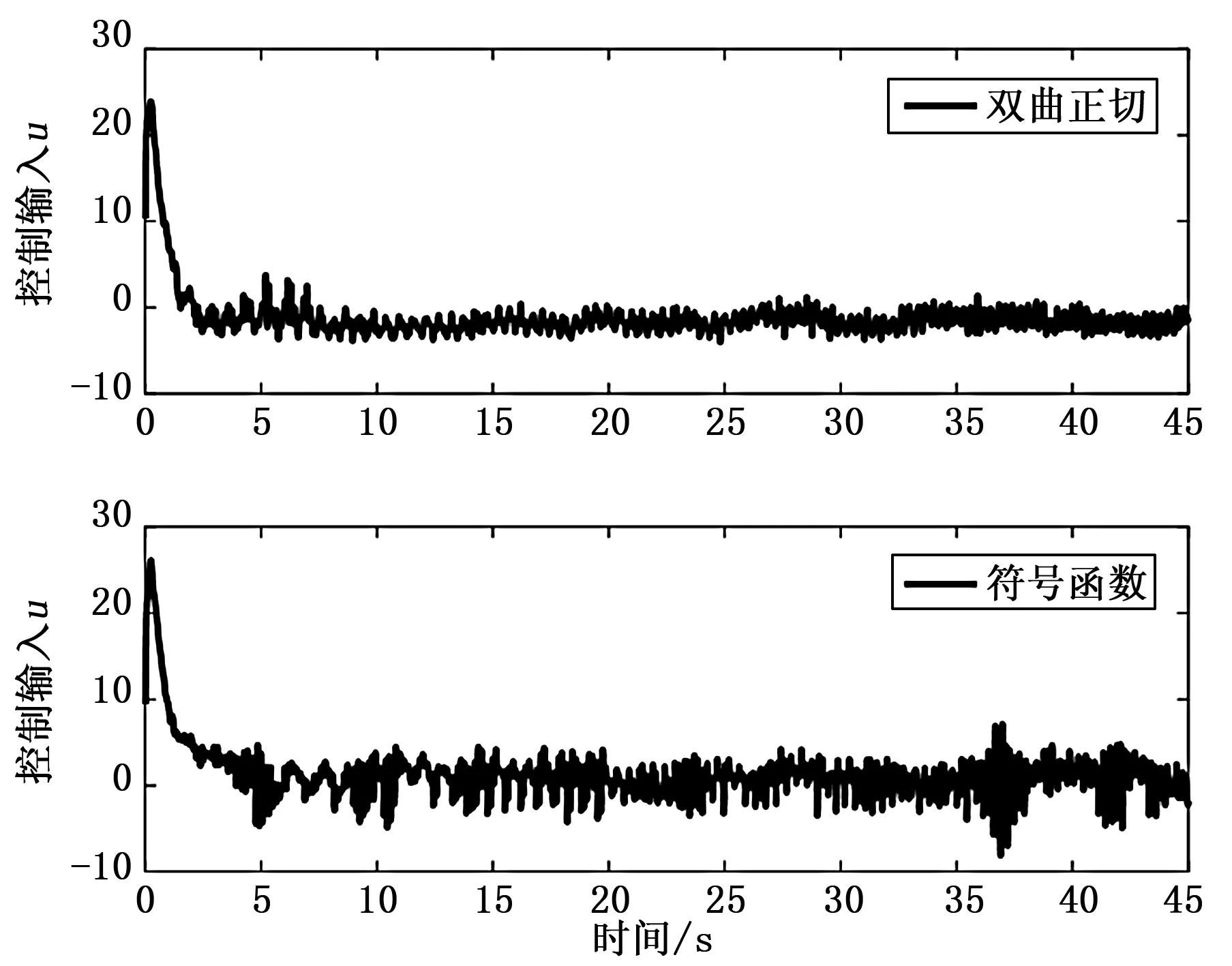
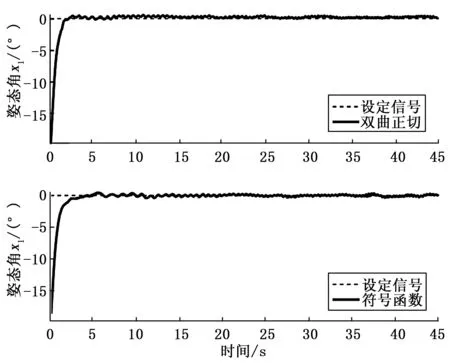
方法一的滑模面siga2e项的幂次系数0 (33) 针对两旋翼飞行器系统式,根据控制律式和式,当滑模变量s=0时,符号函数sgn(·)不连续性,会导致系统颤震。在实验过程中,为了消除符号函数不连续性,可以采用分段函数替换,如文献[19]采用以下函数: (34) 式中,ζ>0,ζ是一个充分小有界正数,代表边界层的厚度。也可采用双曲正切函数替换符号函数: (35) 式中,ρ>0,参数ρ越大,双曲正切函数越接近于符号函数,则控制律式和式获得控制性能越好。在实验过程中,如果能够选择合适的参数ρ或ζ,则可保持系统颤震和跟踪性能之间的平衡。 1)矩形波跟踪实验: 表1 矩形波跟踪实验的控制参数 图4 幅值25°矩形波的跟踪轨迹 图5 幅值25°矩形波时的 图6为方法一在不同系统姿态角初始状态的收敛情况,其中实验的参考轨迹为xd=0°,系统姿态角x1初始值x1(0)分别为-50°~-5°区间之间的6个初始值,其它控制参数和实验条件同上述实验。从图6明显地看出,姿态角x1(0)初始值绝对值越大,系统状态变量收敛时间越长,实验结果与理论分析保持一致,即收敛时间与系统初始值有关。 图6 参考轨迹xd=0的跟踪轨迹 2)S曲线跟踪实验: 为了进一步验证所提控制方法的跟踪性能,设计S曲线作为对比实验参考轨迹,系统姿态角x1初始值x1(0)为25°,姿态角速度x2初始值x2(0)为0°/s,系统控制参数由表2获取,图7是设定信号为S曲线的跟踪轨迹。 表2 S曲线跟踪实验的控制参数 图7 S曲线的跟踪轨迹 由图7可以看出,方法一与方法二相比,方法一对姿态角x1跟踪具有更快收敛速度。 3)替换符号函数对系统控制性能影响: 为验证所提控制方法的符号函数被替换,对系统控制性能的影响,设计实验参考轨迹为xd=0°,作为方法一的设定信号,系统姿态角x1初始值x1(0)为-20°,系统控制参数由表1获取,其它实验条件同矩形波跟踪实验。 针对符号函数不连续性导致系统颤震。为消除系统颤震,实验过程中采用式双曲正切函数替换符号函数,其中ρ取3。图8和图9分别为未替换符号函数和双曲正切函数替换符号函数的系统控制输入u和系统姿态角x1的跟踪轨迹。 图8 比较双曲正切函数与符号函数对系统性能影响的控制输入u 图9 比较双曲正切函数与符号函数对系统性能影响的姿态角x1的跟踪轨迹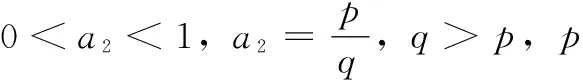
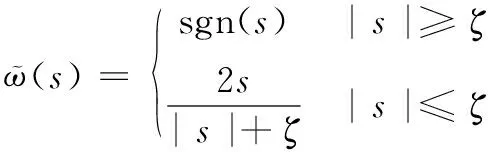
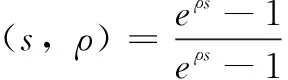
4.3 实验结果分析
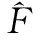

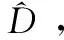


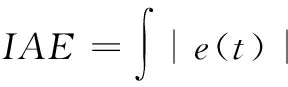
5 结束语


