基于冗余度的复杂网络抗毁性及节点重要度评估模型

王梓行，姜大立，漆 磊，陈 星,赵禹博

(1.陆军勤务学院 a.军事物流系；b.基础部，重庆 401311；2.陆军装甲兵学院士官学院，长春 130137)

0 引言

随着复杂网络研究的逐步深入及其研究方向的不断拓展，复杂网络理论已经更加广泛地应用于当今时代的各个领域之中。然而，任何领域的复杂网络中均分布着不计其数的网络节点，并且节点与节点之间可能又具有错综复杂的连接关系，倘若某些“关键节点”遭受损坏或发生事故，便可能引起“级联失效”的情况，使得网络抗毁性骤降，最终导致网络大规模失效乃至整个系统面临瘫痪的状态。因此，复杂网络抗毁性的量化及节点重要度的评估长期以来一直是此方向的研究热点，它能对整个网络结构的优化、抗毁性的提高以及网络中重要节点的获取与防护提供有效参考和决策支持，对于保证电网、物流网、通信网等领域网络的安全可靠和功能稳定性有着重要而深远的现实意义。

在涉及复杂网络抗毁性和节点重要度问题的相关研究中，从模型构建的角度上来看，现有文献很少使用概率对网络抗毁性进行量化，故不利于各种抗毁性求解方法在求解效果和结果精度上的相互比较；另外，现有研究多以网络中的局部属性作为节点重要度的评价指标，而通过网络全局属性进行重要度评估的研究不多、成果偏少，且建立的模型大多复杂程度较高，故对于规模较大的复杂网络适用性不强。吴俊等[1]针对网络结构属性，利用网络中所有回路数的加权和对任意两点间可替代路径的冗余程度进行量化，而后借助特征谱理论对网络的自然连通度进行定义，并将其作为谱测度指标对网络抗毁性展开量化；田田等[2]以自然连通度为基础构建了针对网络抗毁性的组合优化模型，并利用改进的搜索禁忌算法对抗毁性最优的网络的拓扑属性展开分析研究；蒋丰景[3]根据度分布和网络的局部连通性，建立了节点重要度量化评估模型，同时提出了一种以重要度熵为基础的方法对网络抗毁性展开度量，对于小规模网络节点重要度和抗毁性的求解具有一定的可行性和有效性；王灿[4]根据复杂网络理论中对熵的定义以及图论中的中心介数理论，在无线传输领域建立了以介数熵为基础的网络抗毁性量化求解模型；姚杰[5]基于复杂网络理论对网络中连接度、中心介数、紧密性和特征向量等重要性评估指标进行分析研究，借助层次分析法建立了基于通信网的节点重要度量化评估模型。本文在已有成果文献的基础上，根据网络中任意两点间替代路径的数量定义了复杂网络的冗余度，同时基于此用网络随机失效后保持连通的概率对其抗毁性进行量化，并利用冗余度在网络中的全局属性对节点重要度进行评估，最终建立起基于冗余度的复杂网络抗毁性及节点重要度评估模型，为大规模网络中关键节点的防护以及复杂网络抗毁性的优化提高提供参考模型和决策依据。

在求解算法方面，现有研究大多难以解决求解精度与耗时长度之间的矛盾：若以网络局部属性的相关算法对节点重要度进行评估，则大都难以取得排序一致且精度较高的解；若以网络全局属性设计算法量化节点重要度，则大多会导致其时间复杂度较高，在评估复杂网络节点重要度上缺乏一定的时效性。谭跃进等[6]通过节点度和平均路径长度的结合，对网络的局部和全局属性进行综合性考虑，以凝聚度为基础设计出了节点收缩法，从而量化评估复杂网络的节点重要性，并获得了理想的运算效率；刘媛妮[7]基于中心介数理论和重要度熵设计出一种网络抗毁性量化算法，并通过节点受损后网络中抗毁性的变化程度来对节点的重要度进行衡量；陈静等[8]借助节点关键度理论及网络节点接近度的概念设计出一种方法以评估各个节点的重要度，在对网络的局部和全局属性展开综合考虑的前提下，提出了针对复杂网络节点重要性的量化评估手段，并且取得了可接受的时间复杂度；张喜平等[9]根据邻居节点理论，以m阶邻居节点的重要度贡献为基础，提出一种精确性较高的方法对复杂网络节点重要性展开评估，同时显著区分了复杂网络中不同节点之间的差异程度；阮逸润等[10]从网络拓扑结构出发，基于网络中节点的局部重合程度对节点相似性进行定义，并由此设计出一种将邻接拓扑重合度和度分布相结合的节点重要度评估方法；宋琛等[11]以随机游走技术为基础设计出一种优化叠加算法的节点重要性量化评估手段，有效解决了当前评估方法中普遍存在的重要度排序结果精确度不高的问题。针对文献分析，本文拟利用网络冗余度的全局属性，通过节点删除的方法对网络中各个节点的重要度进行评估，为有效处理求解精度与算法复杂度之间的矛盾提供参考。

1 模型的准备

1.1 问题提出

在当今社会中复杂网络几乎随处可见，其理论对于各个领域均有极其重要的运用价值。然而，一旦网络中部分关键节点受损或失效，轻则造成网络连通性的下降，重则可能导致整个网络陷入瘫痪的状态。因此，对于复杂网络抗毁性及其节点重要度的评估具有重要而深远的现实意义。

本文从拓扑结构的角度出发，将复杂网络视为一个包含n个点、m条边的无向无权图G=(V,E)。其中，V={v1,v2,…，vn}为图G的非空节点集，E={e1,e2,…，em}⊆V×V为图G的非空边集。则图G可通过邻接矩阵A(G)=(aij)n×n进行简化表示，其中，vi与vj相连通则取aij=1，不连通则取aij=0，此外，该邻接矩阵A(G)中的aii=0且aij=aji。要求根据网络拓扑结构及其节点连接情况，建立一个普适性的数学模型，从而量化出复杂网络的抗毁性，同时对网络中各个节点的重要度进行评估。

1.2 模型假设

1)各个领域的网络均存在复杂度上限，且复杂度最大的网络是一个节点数确定的完全图。

2)节点在网络中有且仅有两种状态——失效和正常，且节点失效是相互独立的。

3)节点失效后原来与其相连的边也将失效。

4)将冗余度作为唯一的评价指标对复杂网络的抗毁性进行研究，不考虑其它因素的影响。

1.3 符号说明

对该模型所用到的符号进行说明(见表1)。

表1 符号类型及含义Tab.1 Symbol types and meanings

2 模型的构建

2.1 复杂网络冗余度

复杂网络的抗毁性在狭义上可定义为：边或点遭遇事故随机失效以后网络的拓扑结构还能保持连通的概率[12]。因此，着眼于拓扑结构的角度展开分析，网络抗毁性可以由任意两节点间保持邻接关系的通路数目来衡量。或者说，复杂网络抗毁性可以由网络中任意节点间部分连通路径失效后剩余的替代路径数目进行表征。然而，对于复杂网络中任意节点间替代路径数目的求解往往难以实现，一方面是网络节点间的替代路径数目统计难度较大，另一方面则是随着网络规模的逐步增大，对复杂网络中替代路径数目的求解可能会形成NP问题[13]。故本文考虑使用复杂网络中的所有闭合回路数来对任意节点间替代路径数的累加和进行简化表征[14]，可认为网络中的闭合回路数越多，网络节点间的替代路径数量就越多，其抗毁性也就越高。

网络闭合回路数是图论中网络的基本属性之一，可与网络子图一一对应。在含有n个点，m条边的无向无权图G=(V,E)中，由于其邻接矩阵A(G)=(aij)n×n是实对称矩阵，故根据矩阵理论可知，该邻接矩阵A(G)有n个实特征值λi，其中，i=1,2,…,n。这里不妨假设λ1≥λ2≥…≥λn，因此，根据邻接矩阵的特征值，可以得出网络的谱密度ρ(λ)，即

(1)

式(1)中：δ(λ)为单位冲激函数，λ=0时δ(λ)=1，λ≠0时δ(λ)=0。

由此可知ρ(λ)是一种谱密度，因为满足

(2)

显然，当n→∞时，ρ(λ)逼近一个连续函数。进一步，根据图论和矩阵特征值理论，可以得出

(3)

(4)

式(4)表示网络G中包含的所有有序闭合回路数可由网络所有阶次的邻接矩阵的迹之和进行度量。其中，tr((A)k)指k次邻接矩阵的迹，λi指网络G的邻接矩阵A(G)的第i个特征值。

(5)

式(5)表示，根据泰勒公式，网络中包含的所有无序闭合回路数可由网络邻接矩阵所有特征值的自然指数和进行度量。此外，为实现数量级的统一同时保证L′处于收敛状态，基于式(5)进行处理，从而定义了复杂网络冗余度

(6)

其中，λi为网络G的邻接矩阵A(G)的第i个特征值。

2.2 基于冗余度的复杂网络抗毁性及节点重要度

在节点数目一定的情况下，基于增删边的网络冗余度变化是严格单调的[16]。因此，网络规模确定的无向图中，完全图的冗余度最大，网络抗毁性最优。此外，将式(6)通过Matlab2012b进行测试后，发现完全图基于节点数目的网络冗余度亦是单调的(见图1)。

图1 完全图冗余度随网络规模扩大的变化情况示意Fig.1 The change of complete graph redundancy as the network scale expands

然而，在实际情况下，任何领域的网络构建都会受到一定成本的约束，因此导致了各个领域的网络都会有网络复杂度的限制[17]。故根据不同领域的网络性质及约束成本，可确定其所能构建完全图网络的最大规模，即完全图的最大节点数——在对模型进行仿真求解时输入其最大节点数，进而可界定出该领域的网络冗余度上限值。

(7)

式(7)表示网络冗余度的上限值，其中，Nm指规模最大的完全图网络的节点数，即此领域中所能构建完全图网络的最大规模。

综上，根据复杂网络抗毁性的定义，基于冗余度的性质利用网络随机失效后保持连通的概率对其抗毁性进行量化

(8)

其中，R为任一领域的复杂网络冗余度。

以上述模型为理论基础，基于网络冗余度的全局属性，通过节点删除的方法对网络中所有节点的重要度进行评估。

当M=3，N=5时，文献[9]和文献[13]的自由度为16，本文算法的自由度为25.为了验证三种算法的检测能力，设置仿真条件：信噪比为10dB，快拍数K=500，信号源数D=13，来波方向均匀分布在-60°～60°范围内，三种算法的归一化DOA检测空间谱如图 5所示.为了验证算法的阵列自由度，同时仿真了信源数增加到20时本文算法的归一化DOA检测空间谱，仿真结果如图 6所示.

(9)

式(9)表示网络G中节点vdel的重要度，可用网络G的初始冗余度与删除节点vdel后新网络G′的冗余度之差再与初始冗余度相除进行表示。其中，P0为网络G的初始抗毁性，Pdel为删除节点vdel后新网络G′的抗毁性，R0为网络G的初始冗余度，Rdel为删除节点vdel后新网络G′的冗余度。

3 模型的求解

3.1 求解思路

首先，将待求网络表示成邻接矩阵的形式代入模型，并根据网络所属的具体领域明确其完全图的最大节点数；其次，分别求解出原网络和最大完全图网络邻接矩阵的全部特征值，同时根据复杂网络冗余度的定义计算出网络的初始冗余度和冗余度上限值；然后基于冗余度用网络随机失效后保持连通的概率对其抗毁性进行量化并输出；最后利用冗余度的全局属性，通过网络初始冗余度与删除节点后新网络冗余度之差与初始冗余度的比值对网络中所有节点的重要度进行评估。模型求解思路示意如图2所示。

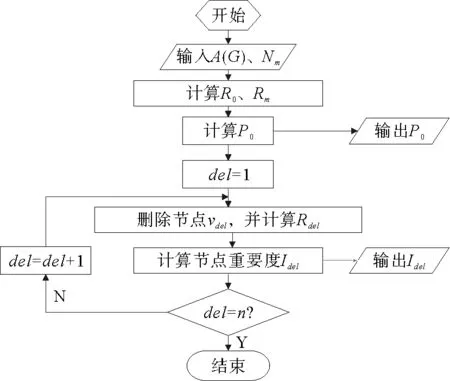
图2 模型求解思路示意Fig.2 Model solution steps

3.2 算法流程及其复杂性分析

步骤1 输入待求网络的邻接矩阵A(G)，以及网络所属领域完全图的最大节点数Nm；

步骤2 计算网络初始冗余度R0和最大冗余度Rm；

步骤3 计算并输出网络抗毁性P；

步骤4 在原网络中删除节点vdel，并计算新网络的冗余度Rdel；

步骤5 计算并输出节点重要度Idel；

步骤6 重复Step4至Step5，直至穷尽网络的全部节点。

表2 网络抗毁性指标的计算复杂度对比Tab.2 Comparison of computational complexity about network invulnerability indicators

由于网络冗余度可直接通过其邻接矩阵的特征谱直接导出，数学形式简洁且物理意义明确，具有良好的计算效果；另外，网络冗余度能够表征网络中任意节点间部分连通路径失效后剩余的替代路径数目，在结合节点删除法后能更精确地刻画出复杂网络抗毁性的细微变化，故此模型算法能有效处理求解精度与算法复杂度之间的矛盾。

4 仿真算例

4.1 问题描述

目前，复杂网络正越来越广泛地运用于社会的各个领域，其指标的研究对于各领域的发展也具有越来越深远的现实意义和重大的应用价值。现针对爵士音乐家合作网络(Jazz)、线虫新陈代谢网络(Metabolic)两个不同类型和规模的真实复杂网络进行数据分析处理[18]，要求分别对各自的网络抗毁性以及节点重要度进行量化求解，同时分别得出各自网络中重要度排名前十的节点序列。

4.2 问题求解

首先，根据Jazz和Metabolic两个真实网络的数据集进行数据处理分析，分别将其转化为对应的邻接矩阵；其次，通过实际调研和专家评价的方式对这两个复杂网络所处领域的完全图最大节点数进行界定——分别为200和500；而后分别将各自网络的邻接矩阵及其完全图最大节点数代入基于冗余度的复杂网络抗毁性及节点重要度评估模型，根据上述算法步骤，借助Matlab2012b进行仿真分析，最终得到各自网络的抗毁性及其节点重要度排序(如表3、4所示)。

表3 Jazz、Metabolic网络的抗毁性对比Tab.3 Comparison of invulnerability in Jazz and Metabolic networks

4.3 结果分析

由表3可以看出，在各领域网络最大复杂度确定的情况下，Jazz网络的抗毁性较好。因此，对于一定约束成本限制下高抗毁性网络的构造问题，Jazz网络能够作为一种较好的参考模板供研究者进行网络结构优化，进而得到抗毁性最优的复杂网络。

为验证本文方法能对节点重要度评估中求解精度与耗时长度之间的矛盾进行有效解决，参考相关文献[19-22]，在Matlab语言环境下分别利用本文方法、基于最短路的接近度方法、基于信息的中心化方法以及节点收缩方法对Jazz和Metabolic网络的节点重要度进行评估，同时利用基于生物学的经典病毒传播模型(SI模型)针对两个网络分别进行节点实际传播效果仿真，得出各种方法的节点重要度评估结果及其节点实际传播能力，从而对不同方法的有效性进行判断，两个网络中不同方法评估结果与节点实际传播效果关系如图3所示。

表4 Jazz、Metabolic网络的节点重要度排序Tab.4 Node importance ranking in Jazz and Metabolic networks

图3 不同方法评估结果与节点实际传播效果关系Fig.3 Relationship between evaluation results of different methods and actual propagation effect of nodes

为了对各种评估方法的有效性进行量化和对比分析，借助Kendall系数(τ)对不同方法评估结果与节点实际传播能力值之间的相关程度进行度量，得到不同方法评估结果与节点实际传播效果的Kendall系数如表5所示。此外，为验证方法的时效性，本文将此方法在不同规模的ER网络中进行模拟仿真，得到其运行时间随节点数目上升的变化情况如图4所示。

表5 不同方法评估结果与节点实际传播效果的Kendall系数Tab.5 Kendall coefficients of evaluation results of different methods and actual propagation effect of nodes

图4 本方法在ER网络中运行时间随节点数目上升的变化情况Fig.4 Running time for the ER network vs number of nodes

在图3中可以直观地看出，本文方法相较于其它重要度评估方法而言，无论针对Jazz网络还是Metabolic网络均更具有效性。根据图3中的b、c和f、g可以看出，基于最短路的接近度方法、基于信息的中心化方法均存在相似节点间实际传播能力值差异偏大的现象，故其在各自网络中所对应的散点图皆不随评估结果单调递增且最终呈现出发散的趋势；根据图3中的d和h可以看出，节点收缩方法针对Jazz网络的有效性和可靠性不高，因此其散点图d中点分布较为分散且无法形成线性的趋势，而针对Metabolic网络而言，节点收缩方法无法对节点重要度进行细粒度区分，故其散点图h中相同横坐标值对应的实际传播能力值不唯一；而根据图3中的a和e则能看出，在不同类型的网络中，本文方法所对应的散点图随评估结果近似呈线性和单调递增的趋势且最终收敛于实际传播能力的饱和值，故在节点重要度的有效评估上较其它方法具有一定的先进性。

表5表示在两个网络中各种方法评估结果与节点实际传播效果之间的相关性，其中，R、Cc、Cv、Nc、SI分别指本文基于冗余度的方法、基于最短路的接近度方法、基于信息的中心化方法、节点收缩方法、基于生物学的经典病毒传播模型。根据表5可以看出，对于不同类型的复杂网络而言，本文方法和基于最短路的接近度方法、基于信息的中心化方法以及节点收缩方法3种计算精度较高的全局性算法相比，与节点实际传播能力值之间的一致程度最高，故说明本文方法在网络的节点重要度评估方面具有一定优越性，能够作为一种新的精度较高的重要度评估手段为网络中重要节点的获取与防护提供参考。

由图4可以看出，随着网络中节点数目的上升算法运行时间将不可避免地处于持续上升的状态，但在相应领域网络最大节点数的限制范围内此运行时间仍是可接受的[23]，因此，在同一类型不同规模的复杂网络中，本文方法仍能保持一定的可行性和时效性。故本文模型算法对于各种类型的较大规模网络中节点重要度的评估具备必要的有效性和可行性。

5 结语

本文从网络拓扑结构的角度出发，针对复杂网络抗毁性及节点重要度评估问题进行了综合性研究。模型方面，定义了复杂网络的冗余度，同时基于此用网络随机失效后保持连通的概率对其抗毁性进行量化，并利用冗余度的网络全局性对节点重要度进行评估，最终建立起基于冗余度的复杂网络抗毁性及节点重要度评估模型，为复杂网络抗毁性的提高以及重要节点的防护提供参考模型和决策依据。算法方面，利用网络冗余度的全局属性，通过节点删除的方法对网络中各个节点的重要度进行评估，从而为解决求解精度与算法复杂度之间的矛盾提供参考。算例方面，利用Jazz和Metabolic两个真实网络进行仿真求解，结果表明该模型算法能为一定约束成本限制下高抗毁性网络的构造问题提供解决方案，同时对于各种类型的较大规模网络中节点重要度的评估具有一定的有效性和优越性。不足方面，在网络抗毁性度量中对完全图最大节点数的界定上缺乏必要的客观性和理论性，下一步将重点针对不同领域中受成本约束下完全图网络规模上限的量化求解问题进行定量化分析和模型化研究。