地表温度降尺度优化研究

臧金龙，国巧真，吴欢欢，乔悦，付盈

(天津城建大学 地质与测绘学院，天津 300384)

0 引言

卫星遥感在地表温度(land surface temperature，LST)反演方面展示出巨大潜力，利用热红外波段数据进行地表温度反演，可快速且方便地获得大范围、较准确、连续变化的地表温度[1]。然而，城市环境的复杂性要求尽可能高的空间分辨率LST来进行城市不同地表覆盖类型热特性的准确描述[2]。由于现有星载热红外传感器技术的限制，这些星载热红外影像的空间分辨率普遍偏低，限制了高空间分辨率的地表温度信息在城市热环境研究、城市能效监测评估、建筑热能消耗检测等研究中的应用[3-4]。为获取满足应用需求的LST产品，利用高空间分辨率影像的波段信息进行地表温度降尺度的技术应运而生。

目前LST的空间降尺度方法主要分为：数理统计回归法、光谱混合模型法和调制分配法，其中较为常用的是数理统计回归法。数理统计回归法的基础假设是关系尺度不变，即LST与回归核的统计关系在各个尺度上保持不变，回归核包括反照率、组分权重和光谱指数等[5]。Kustas等[6]首次提出利用LST与NDVI的关系来实现 LST降尺度的DisTrad算法，通过建立二者间的二次回归模型，成功实现对千米级到百米级LST的降尺度。Agam等[5]对DisTrad算法进行了改进，通过在对 LST与4种植被指数进行回归分析的基础上提出了TsHARP算法，该算法认为利用LST与植被覆盖度之间的一元线性关系能够达到更好的降尺度效果。Essa等[7]指出对于下垫面复杂的城市地表，利用不透水面积指数建立模型比NDVI的效果更好。近几年也有研究表明，对于不同的地表覆盖特征，综合利用NDVI、EVI、NDBI及UI等光谱指数对地表温度降尺度的效果优于单一指数的效果[8-10]。

上述研究已经取得突破性的进展，但仍存在一些不足。在分辨率方面，目前许多卫星携带的多光谱成像仪获得的影像分辨率都优于30 m，将地表温度表现在更小尺度内的方法有待研究。在精度方面，许多研究先将高分辨率的LST数据聚合至低分辨率后进行降尺度处理，原始LST数据在重采样或升尺度过程中会产生新的误差，对结果产生较大干扰。在结果验证方面，多数研究用反演后的相对较高分辨率的LST数据对降尺度结果进行验证，由于温度反演过程本身存在误差，验证结果的可靠性不强。针对以上问题，本文利用Sentinel-2卫星的10 m分辨率数据，直接对反演的30 m分辨率LST进行降尺度研究。对于因城市下垫面复杂导致的降尺度精度问题，基于对温度图像梯度的分析，通过利用空间滤波方式改善温度梯度的分布来降低结果误差。对于最终降尺度到10 m分辨率的LST数据，利用实地测量的温度进行验证。

1 研究区与数据源

研究区包括天津的中心城区及附近郊区，如图1所示。其地理范围为116° 54′ 53″E～117° 22′ 48″ E、38° 55′ 27″N～39° 17′ 6″N，研究区属于暖温带半湿润大陆性季风气候，地势平坦，地表覆盖类型丰富。街道、建筑物、植被和水域等地物交错分布，空间异质性高，作为地表温度降尺度的研究对象具有代表性。天津市春季降雨少、天气晴朗，卫星影像质量高，因此选取的研究时段为4月。

图1 研究区与测量方法

本文用于地表温度反演的数据来自Landsat-8的OLI和TIRS传感器，Landsat-8 OLI的1～7波段分辨率为30 m，TIRS的分辨率为100 m。成像时间为2017年4月，轨道号为122-33，影像下载于美国地质勘探局(http：//glovis.usgs.gov/)。本文使用的高分辨率影像来自Sentinel-2 MSI传感器。Sentinel-2 MSI共有13个波段的影像，其中，10 m高分辨率的波段有蓝波段、绿波段、红波段和近红外波段。影像成像时间为2017年4月，轨道号为N0205-R032-T50SMJ和N0205-R032-T50SNJ，影像下载于科学网(https：//scihub.copernicus.eu/)。实地测量数据在2017年4月Landsat-8卫星过境时采集，测量位置与方法如图1所示。使用温度计为主要测量工具，测量每一个点位时，将温度计的感温泡与地面充分接触，并用手持GPS进行定位。所有实测点均在卫星过境时刻附近完成测量，因受影像成像时间限制，共得到33个实测点数据(表1)。

表1 测量地点名称和LST

2 研究方法

2.1 地表温度反演

有研究表明，单通道算法(single channel，SC)基于Landsat-8 TIRS数据反演地表温度具有很好的精度和敏感性[11]，故本文使用SC进行LST的反演。SC的计算方法如式(1)所示。

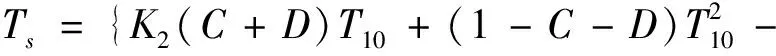
K2DTa}/(K2C)

C=τε

D=(1-τ)[1+(1-ε)τ]

Ta=16.011 0+0.926 21t0

T10=K2/ln(1+K1/L10)

L10=(gain)·DN+(offset)

(1)

式中：Ts为反演的地表温度；T10为TIRS10的亮度温度，单位为K；Ta为大气平均作用温度，单位为K；C和D为中间变量；τ为大气透过率；ε为地表比辐射率；t0为地面附近的气温，单位为K；对于TIRS10，K1=774.89 W·m-2·sr-1·μm-1，K2=1 321.08 K；L10为TIRS10的热辐射强度值，单位为W·(m2·sr·μm)-1；DN为影像的灰度值；gain为增益值；offset为偏移量，可以从数据头文件中直接读取。

对于ε的计算，城镇和自然表面的地表比辐射率εbuilding和εsurface可由公式(2)求得。

εbuilding=PvRvεv+(1-Pv)Rmεm+dε

εsurface=PvRvεv+(1-Pv)Rsεs+dε

Rv=0.933 2+0.058 5Pv

Rm=0.988 6+0.128 7Pv

Rs=0.990 2+0.106 8Pv

Pv=(NDVI-NDVIs)/(NDVIv-NDVIs)

(2)

式中：Rv、Rm和Rs分别为植被、建筑和裸土的温度比率；εv、εm和εs分别为植被、建筑和裸土纯净像元的地表发射率，其值分别取0.986、0.980和0.972；dε为比辐射率修正项，当Pv≤0.5时，dε为0.003 8Pv，当Pv>0.5时，dε为0.003 8(1-Pv)；Pv表示植被覆盖度情况，可由NDVI来计算；NDVIv和NDVIs分别表示纯植被像元与纯裸土像元的NDVI值。本文通过统计影像NDVI直方图，取5%和95%的累积百分比作为置信区间，截取NDVI的上下限阈值分别作为研究区的NDVIs和NDVIv值。

2.2 地表温度降尺度

LST从高尺度向低尺度转换时，通常需要补充额外的信息来构造趋势面。最早提出的DisTrad算法就是通过引入NDVI或其他指数构造趋势面，其基本假设是LST和植被指数的关系在各个尺度上基本一致[6]。以Landsat-8数据为例，首先建立30 m尺度上LST与趋势面因子(NDVI)的关系，通过回归分析构造LST与NDVI之间的函数关系。假设此函数关系仍然适用于10 m尺度上的LST与NDVI，此不变性是降尺度技术的基础，也是关键所在。最后，将10 m尺度上Sentinel-2的NDVI值代入此函数关系中，计算得到10 m尺度上的LST。在构造30 m尺度上二者的函数关系时，应选择尽可能多的随机点，以保证关系的可靠性。比较多种回归方式，选择最佳关系式可以确保得到最小残差和最大相关系数。

2.3 温度梯度评价与误差评价

梯度反映了相邻像元的亮度变化率，图像中如果存在地物边缘或者像元亮度差较大时，会出现较高的梯度值[12]；在地表温度的图像中，温度像元差值较大时，亦是如此。由于光谱指数法降尺度的原则是，相同光谱指数值具有相同的温度值，这就导致降尺度后的地表温度在地物交界处易出现较大的波动。运用梯度分析的方法可以有效检测出这种波动，常用的梯度分析方法有罗伯特梯度、索伯尔梯度和拉普拉斯算法。索伯尔梯度与其他2种算法相比，既考虑了更多邻域点的关系，也较好地保留了原图像的特征[13]，故本文采用索伯尔梯度对温度图像的梯度值进行计算，其计算如(3)所示。

|gradf|≌|t1|+|t2|

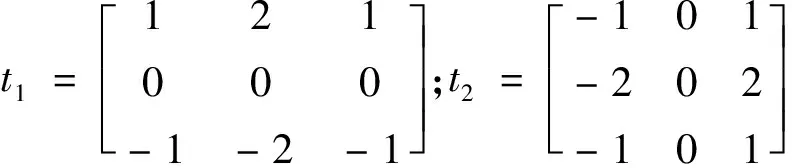
(3)

式中：gradf为梯度计算的结果；t1，t2为计算模板。

温度图像中的突变梯度值分布越多，温度的高低变化越不连续。为了评价图像中突变梯度值的分布，本文提出了梯度异常频率(gradient anomaly frequency，GAF)，即图像中突变梯度值占全部梯度值的比例，表达如式(4)所示。

(4)

式中：n为图像像元的总个数；nm为突变梯度值的个数。对于突变梯度值的界定，本文选取了降尺度之前图像中的100个地物边界附近的梯度值并求其平均值，将大于或等于这个平均值的梯度值界定为梯度突变值。同时，本文也选择了平均绝对误差(MAE)和均方根误差(RMSE)2个指标进行误差评价，MAE和RMSE的计算分别如式(5)和式(6)所示。

(5)

(6)

2.4 滤波处理

热传导在二维平面的传播可简化为式(7)[14]。

(7)

式中：∂u/∂t为平面中一点的温度对时间的变化率；∂2u/∂x2与∂2u/∂y2为温度对2个坐标轴的二次导数；k为热扩散率。此公式表明，任何一个不同的初始温度，经过一定时间都会与周围形成热平衡。因此，热方程的结果具有将初始温度平滑化的特质，这与遥感图像处理中的均值平滑模板作用十分相似。利用NDVI与LST的关系进行降尺度后，由于没有考虑到相邻像元的关系，图像上存在很多梯度异常值。根据温度的热传导特性，本文利用均值滤波方法处理降尺度后的温度图像，以提高图像中温度的连续性。均值滤波的计算如式(8)所示。

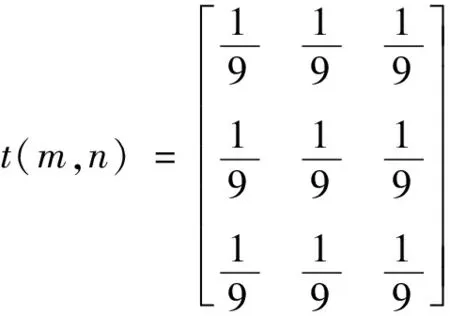
(8)

式中：r(i，j)为计算结果；I(m，n)为降尺度后图像的活动窗口；t(m，n)为均值滤波模板。

3 结果分析

3.1 地表温度反演及降尺度

通过SC算法反演的30 m分辨率LST如图2(a)所示。图中LST变化比较连续，但由于分辨率低，许多细节处的温度无法表现。在研究区内随机选取5 000个点，提取对应点位的LST和NDVI数值并进行拟合。经过多次实验发现，二次拟合模型(式(9))具有较好的相关性，其R2为0.615，拟合结果如图2(c)所示。

图2 反演的30 m分辨率LST与NDVI的拟合结果

LST=-213.19NDVI2+68.131NDVI+27.538

(9)

对Sentinel-2 MSI的波段数据进行辐射校正和大气校正后，计算得到10 m分辨率NDVI。利用NDVI与LST的二次拟合模型(式(9))，计算得到10 m分辨率LST，结果如图3所示。

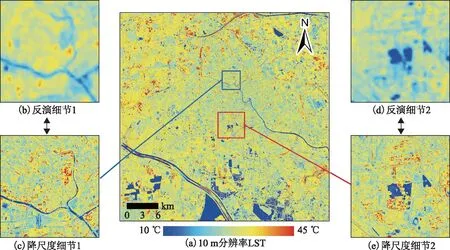
图3 降尺度后的10 m分辨率LST

由图3可以看出，光谱指数法降尺度的温度大体分布特点和反演后的结果相同。随着图像分辨率的提高，更多地物温度的细节被表现出来，对比反演的细节部分结果(图3(b)、图3(d))，很大程度上提高了图像信息量(图3(c)、图3(e))，在地物覆盖类型复杂的区域，能够准确地区分不同地物之间温度的差别。然而此结果也存在较多误差，由于未考虑相邻像元的关系，图像连续性较差，许多位置出现了较大的温度差。尤其是河流与陆地之间，其温度界限过于“明显”，在实际环境中，这些温差较大的区域并不能达到热平衡状态。

3.2 温度梯度与误差评价

利用索伯尔梯度算法对降尺度前后的温度图像梯度进行检测(图4(a)、图4(c))，并选取降尺度之前温度图像中地物边界附近的100个梯度值的平均值作为突变梯度值nm，对GAF进行计算，结果如图4(b)、图4(d)所示。由于反演的LST是根据热红外波段影像计算的结果，其保留了实际温度的宏观分布特点，所以将反演后LST的nm作为参考值计算其他温度梯度图像的GAF。

图4 降尺度前后温度图像梯度与GAF结果

由图4(a)可知，降尺度之前的温度图像梯度整体差别较小，异常梯度分布比较稀疏，异常梯度值只占了总数的3.1%。一般情况下，在地物属性差别较大的区域(如水体和地面分界处)，不可避免会出现少量梯度异常值(图4(b))，所以可以推断，降尺度之前的温度图像基本符合热平衡规律。而图4(c)中，温度梯度值高低交错、变化频繁，异常梯度分布十分密集，异常梯度值几乎占总数的一半，尤其是中心区域，遍布了大量的高异常梯度值(图4(d))。由此可见，光谱指数法降尺度后，像元存在严重的独立性，几乎和相邻像元脱离了关系，造成温度变化非常不均匀。通过图5的误差评价发现，温度的准确度也大幅降低。

降尺度后的MAE和RMSE达到了降尺度之前的2倍以上，大部分温度与实际测量温度差别较大，最大误差达到了11.7 ℃，比降尺度之前的最大误差高出6.9 ℃。由图5同时可以发现，降尺度之前25～33号点位的温度普遍低于实测温度，而这部分点位大多处于高温段。其原因可能是由于反演后温度图像分辨率低，温度像元覆盖的地面范围比较大，不能准确体现小尺度区域的高温点信息所致。

图5 降尺度前后LST误差评价

3.3 LST降尺度结果优化

对降尺度后的温度图像进行均值滤波处理的结果如图6所示。由图6可知，图像在经过滤波处理后，温度的整体分布趋势无较大变化，而图像中高温点和低温点明显有所减少。这说明由于均值滤波的作用，图像中的极端温度值被削弱，极高或极低的温度值减少。由温度图像的细节可以看出，温度变化的连续性有大幅提高，温度高低交错的情况明显减少(图6(b)、图6(c))。可见均值滤波处理改善了像元之间的关系，使大部分温度呈均匀变化，均值滤波后的梯度和误差如图7所示。

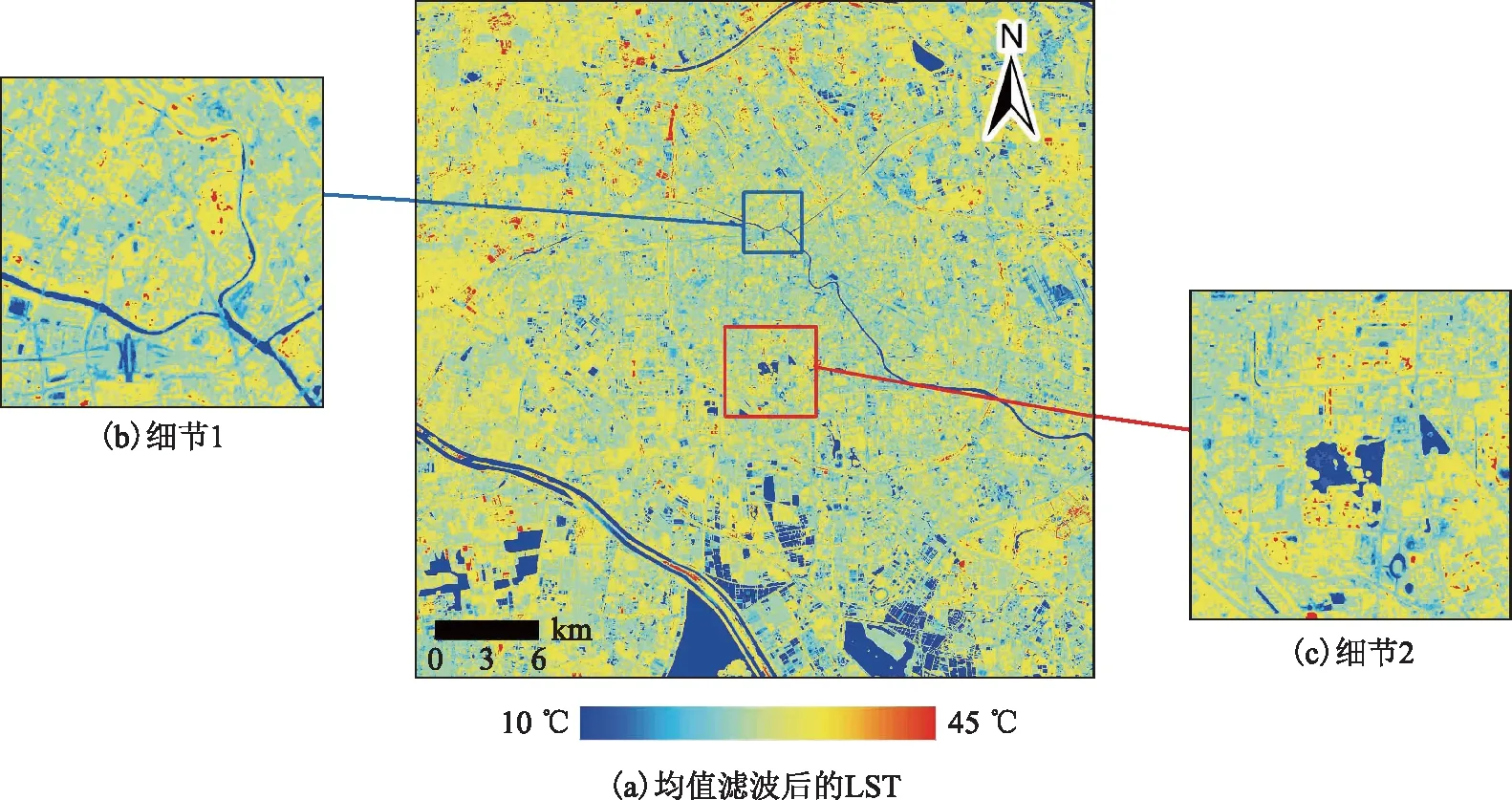
图6 均值滤波处理后的温度图像

由图7(a)和图4(c)对比可知，均值滤波处理后，大量高梯度值变成了低梯度值，部分梯度值降低到了0，整体梯度水平下降。GAF降低到了32.1%(图7(b))，异常梯度值的分布相比处理之前更加稀疏，说明温度突变值有相应减少。对比图7(c)与图5(b)，MAE和RMSE均有小幅度下降，最大误差值也下降了2.6 ℃，说明均值滤波处理后温度图像的精度有一定提升。然而，均值滤波后的GAF与反演后温度图像的GAF仍相差较大，若以反演后温度图像梯度作为参考的热平衡状态下的梯度，均值滤波后温度像元之间的关系并不理想，GAF仍有很大的改善空间。

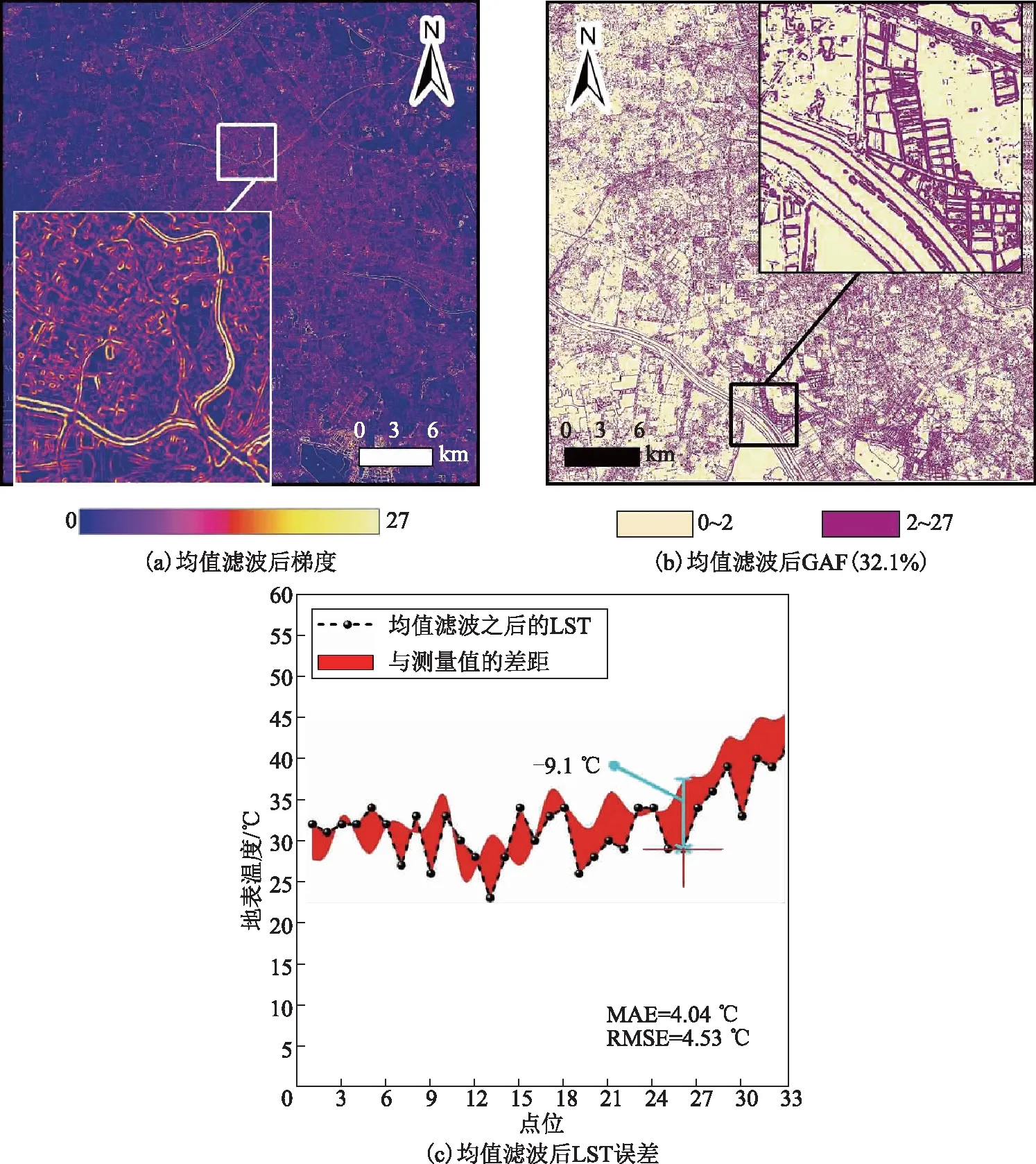
图7 均值滤波处理后梯度检测和误差

4 讨论

本文将梯度分析的方法引入到温度图像的分析中，获得的温度梯度图像直观地展示了温度像元的连续性，是LST降尺度结果分析的一个重要补充。本文提出的GAF是对温度图像梯度的量化评价，同时包含了温度的连续性信息。GAF可作为温度图像评价的一个重要指标，对温度反演及计算结果的合理性有一定指示作用。对于LST降尺度结果的优化和降尺度方法的适用性，本文进行了以下讨论。

由于用3×3均值滤波模板处理后的温度图像梯度还有一定的改善空间，为了使GAF进一步减小，本文通过扩大模板选区来提升滤波强度，讨论了用5×5和7×7像元范围的滤波模板对降尺度后温度图像进行处理的效果(图8)。

由图8可以看出，随着滤波强度的增加，图像梯度进一步改善，温度精度也再一次提高。5×5和7×7模板对图像梯度的处理效果依次增强(图8(a)、图8(b))。尤其是图8(b)中，GAF已经非常接近反演后的水平，而且，异常梯度分布非常稀疏，主要分布在地物边界附近。然而，在用5×5模板以上的滤波强度时，温度图像的精度几乎无变化(图8(c)、图8(d))，说明图像梯度改善到一定程度时，其对温度精度的提高作用不明显，而此时的温度误差已不再是由像元不连续造成的。7×7模板处理后的图像不仅精度高，且具有最佳的GAF值，因此7×7模板达到了最优的均值滤波效果。图9展示了运用7×7模板处理后温度图像更多的细节。

图8 不同强度的均值滤波算子对GAF和误差的影响

从图9的三维温度细节中可以看出，7×7均值滤波模板处理后的图像效果很好，像元高低变化连续，无温度突变的情况。从图9中一处水域附近的温度分布来看，极高温度与极低温度之间温度变化自然、均匀，已基本符合热平衡状态的特点。

图9 7×7均值滤波模板处理后的温度图像空间立体展示

均值滤波处理虽然有效改善了降尺度后图像的梯度，也提高了温度图像的精度，但提高后的精度距离反演后的精度还有一定差距。通过对比图10(a)和图10(b)发现，均值滤波处理后的图像在高温区域和低温区域还存在比较明显的误差，而这些误差主要是在降尺度过程中出现的。对于光谱指数降尺度方法本身存在的缺陷，未来研究可以将反演的LST作为参考值，和降尺度后对应位置的温度像元建立联系，从而控制降尺度后的温度分布。若能发挥反演后LST的监督作用，再利用本文的处理方法，应能使降尺度后温度图像的精度进一步提高。

图10 高、低温区域存在的误差

本研究同时发现，GAF的降低虽然能够改善光谱指数法降尺度后温度图像的精度，但它的值并不是越小越好。在本文所选的研究区中，GAF在10%左右变动时，温度精度几乎无变化，此时的温度像元达到一个模拟的热平衡状态，其他区域是否也满足这个规律还有待实验验证。此外，运用SC算法反演的LST本身就存在误差，若能利用真实测量温度与反演的LST建立函数关系，并对反演的LST做初步优化，再进行后续操作，可能会取得更理想的效果。

5 结束语

本文以天津市中心城区及附近郊区为研究区，利用SC算法对LST进行反演，并用光谱指数法对反演的LST进行了空间降尺度，成功将30 m分辨率LST降低到了10 m。降尺度后的LST通过均值滤波处理进行了改善，并基于梯度分析和真实测量温度对结果进行了评价。

运用光谱指数法对反演的LST降尺度到10 m分辨率，可表现出更多地物温度的细节。但由于该方法未考虑相邻像元的关系，导致温度图像连续性差、GAF剧增、温度精度降低。通过3×3均值滤波模板处理后，图像连续性大幅提高；异常温度梯度减少，GAF降低；温度精度也有小幅度提高。加大均值滤波的强度，温度梯度与温度精度会进一步改善。而滤波强度增大到7×7像元范围时，温度精度便很难再提升。运用7×7模板处理后温度图像的效果最理想，像元高低变化连续，基本符合热平衡状态的特点。

均值滤波处理虽然有效改善了降尺度后温度图像的梯度和精度，但对于光谱指数法本身存在的缺陷无法弥补。未来的研究还需要综合反演LST与真实测量温度的特点建立相关关系，进一步优化LST降尺度的结果。