模糊需求下保障设施选址- 路径模型及算法*

孙 凌，梁 明，罗长远

（1.河南牧业经济学院信息工程学院，郑州 450044；2.解放军31674 部队，拉萨 851400，3.信息工程大学，郑州 450001）

0 引言

为实现有效的装备保障，保障系统的快速反应能力就尤为突出。在保障系统中，仓库、补给站等保障设施是为被保障单位提供保障服务的基地，其位置及配送路线的合理与否，直接关系着保障系统能否在有效的时间范围内提供保障服务、所提供保障服务的效率高低以及保障成本高低，直接影响着保障系统对保障需求的反应能力。因此，保障设施的选址-路径决策成为战时保障的重要研究内容。

选址-路径问题是物流管理中开展最早、研究最多的一类集成优化问题。文献［1］研究了多期离散设施选址-路径问题；文献［2］对平面内单设施选址-路径问题进行了研究，并用分层算法进行求解；文献［3］对模糊需求下的选址-路径问题进行了研究，并用混合模拟退火算法进行求解；文献［4］研究了工业有害废物处理中心的选址-路径问题，涉及到废物的收集、运输、处理、回收等多个环节；以上文献在对选址-路径的研究中，没有考虑仓库及运输车辆容量的限制。文献［5-11］分别用不同的方法对有容量限制的选址-路径问题进行了研究，但其客户的需求量都是确定的。由于战斗的突发性及高消耗性，导致前方作战单元只能对自己的需求量提供一个大概的数值，而运输车辆在到达作战单元之前并不知道确切的需求量，因此，在预先计划的运输线路上，可能使得累积需求量超出车辆的容量限制，保障无法继续进行。

本文针对被保障单位需求量不确定现象，建立了模糊需求下带有时间窗及容量限制的选址-路径模型，并设计了基于聚类分析与蚁群算法的混合启发式模型求解算法。

1 保障设施选址-路径相关因素分析

1.1 模糊需求量分析

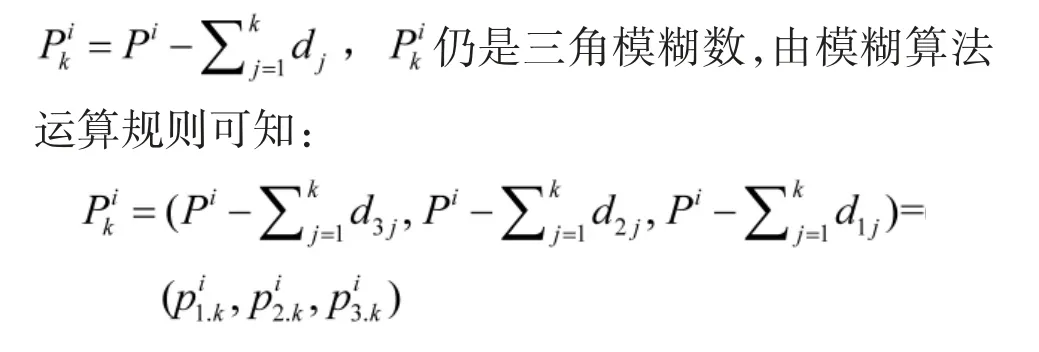
第k+1 个作战单元的需求量不超过保障基地库存剩余量的可信度为：

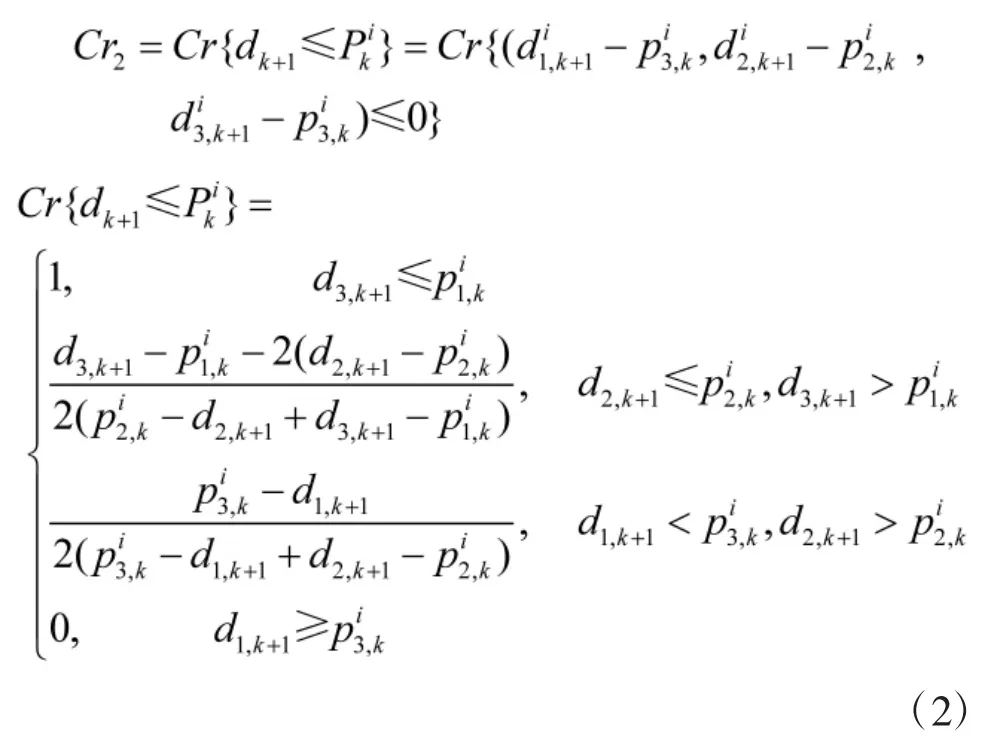
1.2 保障设施备选址评价

初步构建保障设施选址方案评价指标体系如图1 所示。这种层次结构的组成元素和构架不是固定不变，保障部门在具体应用时可根据不同的评价对象对图1 进行适当调整。结合模糊综合评价与群决策思想，用于确定保障部门对各备选方案的综合评价值，步骤如下：

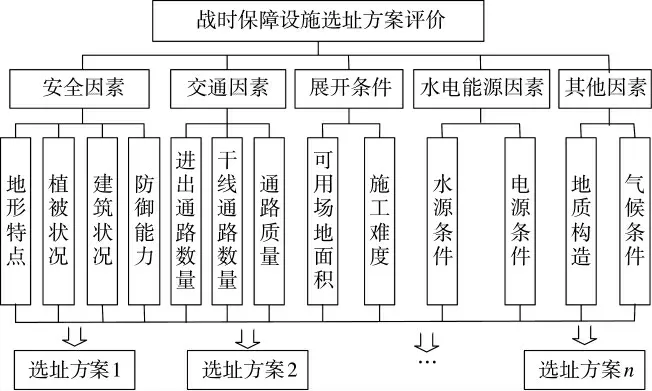
图1 选址决策评价指标体系

Step1：确定隶属度

假设有s 个决策组，以m 个评价指标对n 个备选方案进行评价，指标特征值矩阵为：

3）按vi*的大小对方案集进行排序，vi*越大，则相应的备选址方案越优。

通过以上模糊群决策过程，保障部门可以综合考虑各保障设施备选址点的众多特性，对可行备选地址点进行科学合理的评价，得到相应的权重值。

1.3 时间满意度及惩罚成本分析

1.3.1 保障时间满意度函数

对于各作战单元来说，除了有最佳保障时段外，为了做好应急准备，其都还有一段对提前到达及超时到达的容忍时限。为了准确刻画各作战单元对保障时间的要求，构建衡量作战单元对保障反应时间满意度的评价函数：

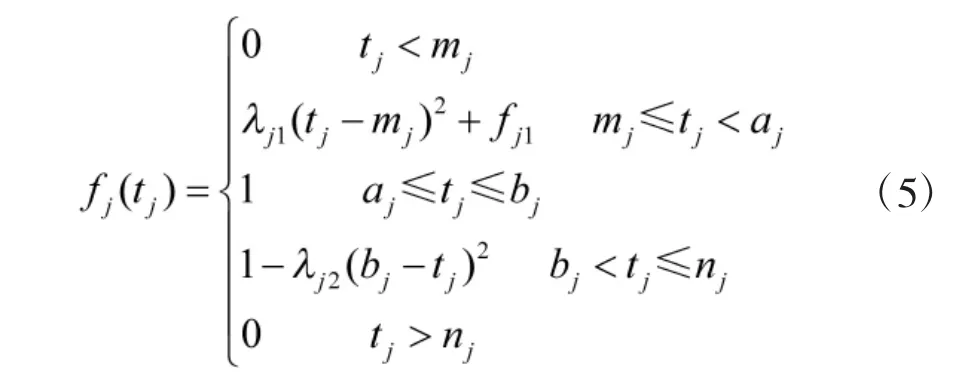
其中，tj表示运输车辆实际到达作战单元j 的时间，mj表示作战单元j 的最大提前到达容忍时限，aj表示作战单元j 的最佳保障时段的开始时间，bj表示作战单元j 的最佳保障时段的结束时间，nj表示作战单元j 的最大超时到达容忍时限。式（5）表示若运输车辆到达时间tj在mj之前，保障时间低于作战单元j 的最大提前到达容忍时限mj，即作战单元j 的满意度为0；当mj≤tj＜aj时，保障时间在作战单元j的提前到达容忍时段内，作战单元的满意度会随着时间的推移而增大；当aj≤tj≤bj时，保障时间在作战单元j 的最佳保障时段内，其满意度为1；当bj＜tj≤nj时，保障时间在作战单元j 的超时到达容忍时段内，作战单元的满意度会随着时间的推移而减少；当tj＞nj时，保障时间大于作战单元j 的最大超时到达容忍时限nj，即作战单元j 的满意度为0。

1.3.2 偏离时间惩罚成本函数

由于每个保障任务中都有时间窗约束（作战单元的最佳保障时间段），当运输车辆未能在时间窗内完成保障任务时，将会产出惩罚成本，且到达时间偏离约束时间窗越多，惩罚成本则越高。构建偏离时间惩罚成本函数：

式（6）表示若运输车辆到达时间tj在作战单元j的最大提前到达容忍时限mj之前，则所造成的惩罚成本为Mj1；当mj≤tj＜aj时，保障时间在作战单元j的提前到达容忍时段内，所造成的惩罚成本将随着时间的推移而减少；当aj≤tj≤bj时，保障时间在作战单元j 的最佳保障时段内，能够圆满完成保障任务，即惩罚成本为0；当bj＜tj≤nj时，保障时间在作战单元j 的超时到达容忍时段内，所造成的惩罚成本将随着时间的推移而增大；当tj＞nj时，保障时间大于作战单元j 的最大超时到达容忍时限nj，则所造成的惩罚成本为Mj2。

2 保障设施选址-路径模型

2.1 模型建立

假设J 为作战单元集合；I 为保障基地候选点集合；V 表示所有点集合，即J∪I；E 表示所有连接两节点（i，j）的集合，i，j∈V；K 表示运输车辆集合。ωj表示作战单元j 处作战任务的成功完成对该次战役任务的重要度；dj表示作战单元j 的需求量；Pi表示保障基地i 的最大库存容量；gij表示节点i 到节点j距离；cij表示两节点（i，j）的单位运输费用，其中（i，j）∈E。f 表示因各路径上的服务失败而产生的额外运输总费用；v 表示运输车辆平均速度。tjk表示运输车辆k 在其路径上到达作战单元j 的时刻；stjk表示运输车辆k 在作战单元j 的保障时间；ltjk表示运输车辆k 在其路径上从作战单元j 离开的时刻；fj（tjk）表示作战单元j 对运输车辆k 保障反应时间的满意度函数；hj（tjk）表示运输车辆k 在对作战单元j 保障时偏离时间的惩罚成本函数。决策变量Zi和Yij表示在创库候选点i 被选中以及为作战单元j 服务时取值1，Wjk和Xijk表示车辆k 为作战单元j 服务以及在其路径上有从i 到j 的路段时取值1；否则取值为0。

在上述分析的基础上，建立了使总选址方案最优，保障成本最小的选址-路径双目标模型：

式（7）表示选址方案最优；式（8）表示保障成本，主要包括计划运输费用、偏离保障时间惩罚成本及考虑服务失败所产生的额外费用；约束（9）表示在车辆容量及可信水平范围内保障所有作战单元；约束（10）表示在保障基地库存容量及可信水平范围内保障所有作战单元；约束（11）保证每个作战单元有且只有一辆车为其保障；约束（12）保证线路中没有子回路；约束（13）与约束（14）保证线路的连续性及车辆返回到起点保障基地；约束（15）表示每个作战单元有且仅有一个候选点为其保障；约束（16）表示两决策变量之间的关系；约束（17）表示前后两连续作战单元上车辆离开时间约束；约束（18）表示运输车辆只有在时间窗口开启保障作战单元之后离开。

2.2 模型求解

基于聚类分析与蚁群算法的混合启发式的模型进行求解过程分为4 个阶段：

1）第1 阶段，作战单元分组

利用聚类分析思想进行分组，作战单元分组要考虑各作战单元的时间窗、作战单元之间的距离、模糊需求量及运输车辆的容量等相关因素。其步骤如下：

Step1：从未分组的作战单元中选择最佳保障时间段开始时间aj最小的作为聚类中心，记为j；

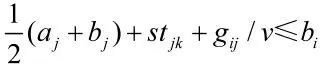
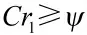
Step4：若还有未检测过的作战单元，则在其集合中执行Step2；否则，执行Step5；

Step5：若还有未分组的作战单元，则新创建一个小组，执行Step1；否则，执行Step6；

Step6：作战单元分组完成，算法停止。

2）第2 阶段，备选址点排序

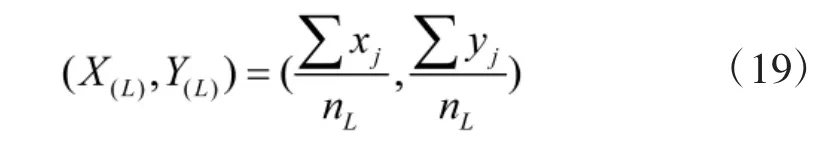
Step2：利用式（20）计算每个组的重心与每个备选点之间的距离之和。

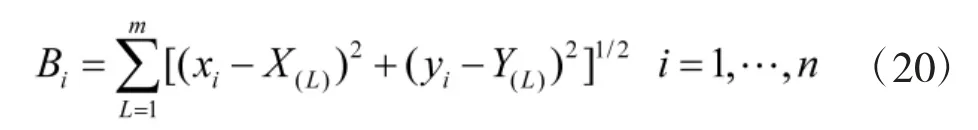
其中，Bi表示备选点i 与所有分组重心点之间的欧氏距离，（xi，yi）表示备选点i 的坐标，m 是小组总数，n 是备选点数。

Step3：根据Bi/vi*的比值大小按升序把备选点从1 到n 排序，并按照此序列选择仓库建设点。

3）第3 阶段，作战单元分组匹配

Step1：计算每个未匹配的作战单元分组重心与未匹配备选点中排名第一者之间的欧氏距离，根据欧氏距离的大小按升序把小组进行排序，并按照此序列对该备选点进行分配；

Step3：对后序作战单元分组执行Step2，直到该备选点剩余库存不能容纳任何一个小组；

Step4：若还有未匹配的作战单元分组，则执行Step1；否则，执行Step5；

Step5：作战单元分组匹配完成，算法停止。

4）第4 阶段，确定线路

①状态转移规则

第k 个路径上的蚂蚁由作战单元i 转向作战单元j 的概率为：

②信息素更新规则

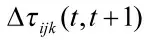
其中，δ 为蚂蚁释放的信息素量的单位长度。

利用上述算法规则，配送路径的求解算法步骤如下：

Step1：初始化各参数；

Step2：设置迭代计数器Nc=0，将m 只蚂蚁放于保障基地，分别为各蚂蚁建立禁忌表；

Step3：对每只蚂蚁i，在已确定匹配关系的作战单元分组列表中找出所有未访问过的节点，根据式（21）计算的概率来选择下一个访问的客户节点j；

Step4：判断作战单元j 的需求量是否超过运输车辆的剩余量，若不超过，则执行Step5；否则，将作战单元j 重新放入集合A 中，并执行Step6；

Step5：判断tjk是否满足时间窗要求，若满足，则把点j 放入禁忌表中，并执行Step3；否则将点j 重新放入集合A 中，执行Step6；

Step6：判断集合A 是否为空，若为空，则执行Step7；否则从集合A 中选择开始时间最早的点作为起点，并执行Step3；

Step7：计算每只蚂蚁走过的每条回路的路径长度，按照各蚂蚁所得到的可行解，得出局部最优解；

Step8：运用2-opt 法对局部最优解进行改善；

Step9：利用式（22）和式（23）进行信息素更新；

Step10：判断Nc＞Ncmax是否成立，若成立，则算法结束，输出计算结果；否则清空禁忌表，执行Step2。

3 算例分析

假设10 个作战单元分散在其作战区域内，即形成了10 个保障需求点。根据该阶段任务的既定作战目标，指挥部门对各作战单元的保障重要度做出了评价，并与作战单元的位置、需求量（单位t）、作业时间（单位h）、约束时间窗及容忍时限等信息绘制成表，如表1 所示。

表1 各作战单元的信息

为了实现及时有效地保障，装备保障部门拟在该保障区域内建立2 个保障基地。保障基地配备运输车辆若干，每辆车载重量均为8 t，车辆平均行驶速度为50 km/h，单位运输费用为50 元/km。根据战场环境保障相关技术部门对作战区域的地形地貌、水电能源条件及道路交通状况等各方面的考察，已确定5 处可行的保障基地备选点，各备选点的权重、地理位置及容量限制（t）等信息绘制成表，如表2 所示。

表2 各备选点的信息

另外，根据作战单元的重要度及保障物资对该单位完成此次任务的重要性，得出各作战单元的保障时间满意度函数及偏离时间惩罚成本函数，其参数如表3、表4 所示。

表3 各作战单元的保障时间满意度函数相关参数

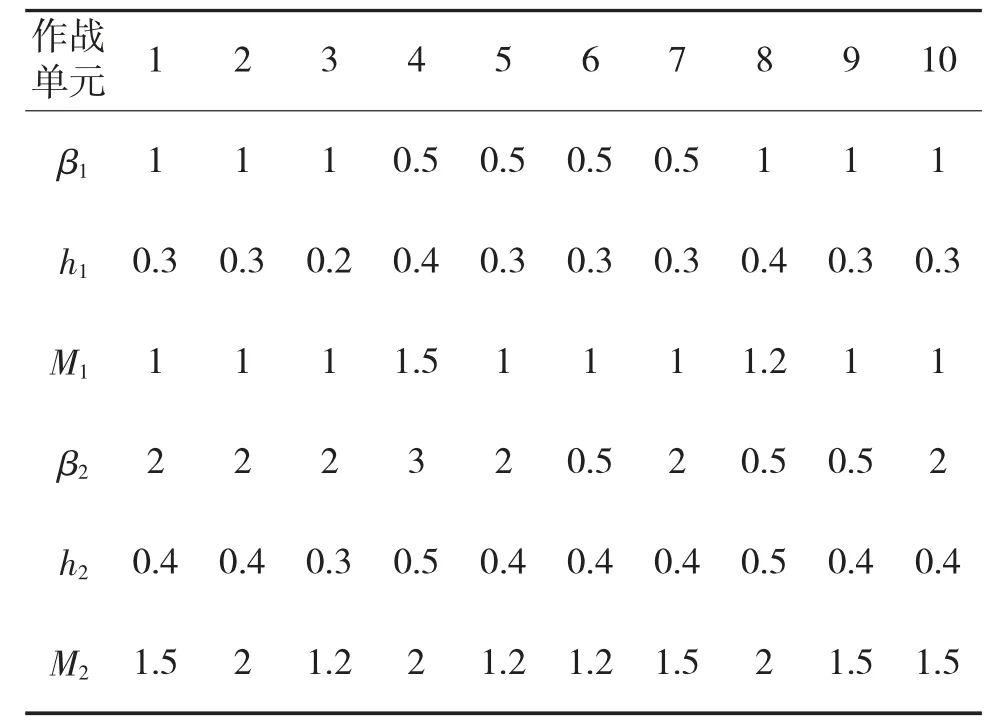
表4 各作战单元的偏离时间惩罚成本函数相关参数

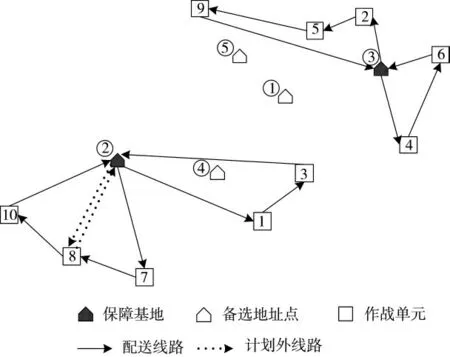
图2 保障物资配送线路规划示意图

依据配送方案，进而得到各配送线路的费用及总方案评价值如表5 所示。从表中可以看出，本文给出的优化方案无论在总费用和评价值方面都具备比较好的优势。这是因为备选点权重优先方案虽然选择的保障基地的权重最高，但缺少考虑路径问题所以带来巨大的费用成本，从而也影响了方案的总评价值；短路径距离优先方案虽然也选择了②、③备选点作为保障基地，并确保了计划费用最小，但是其缺少考虑时间限制因素，导致了较高的惩罚成本。

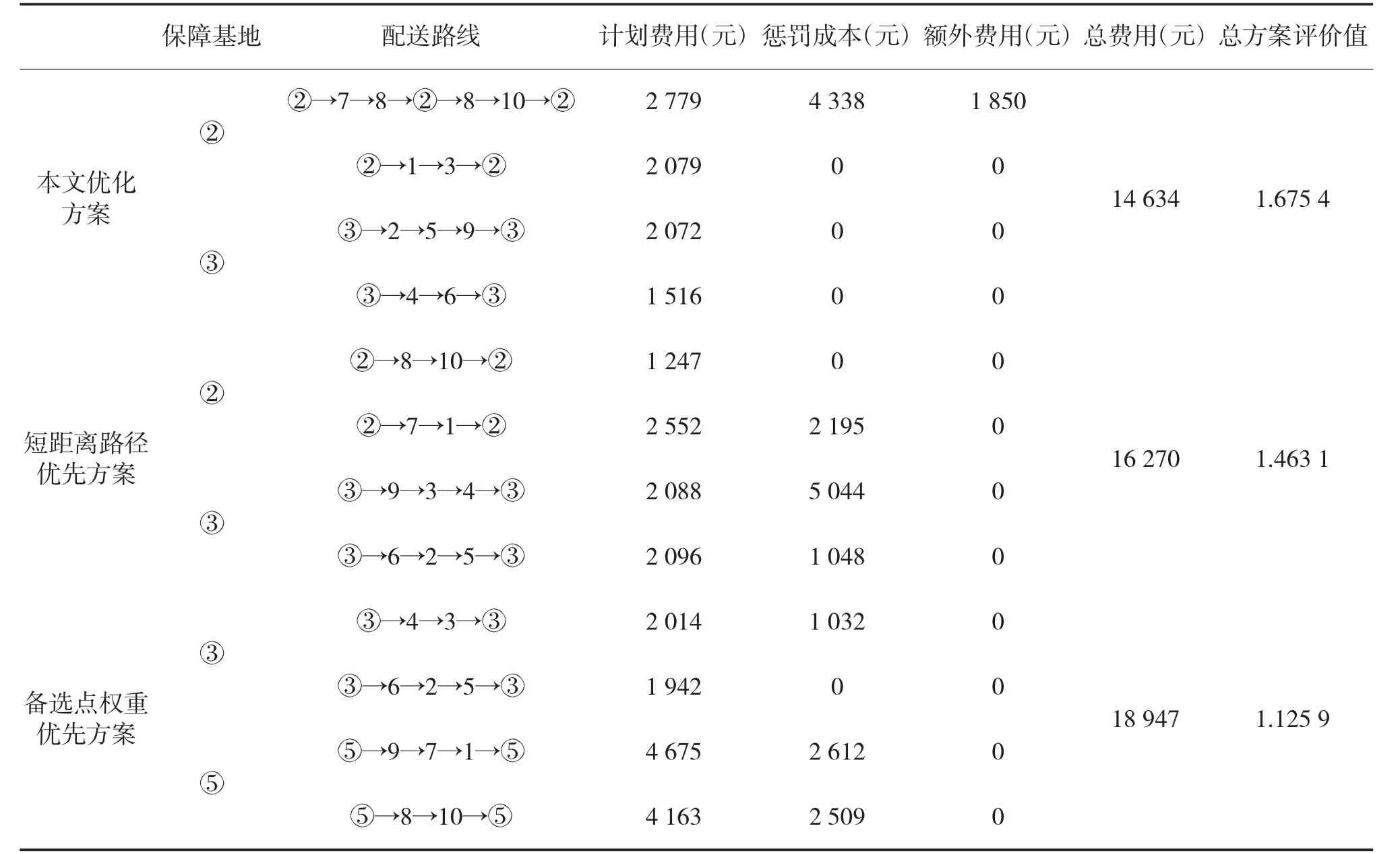
表5 选址-路径方案及相应数据

4 结论

针对装备保障过程中被保障单位需求量不确定的问题，对模糊需求下带有时间窗及容量限制的选址-路径问题进行了研究，建立了相应的模型，结合对模型的分析，设计了基于聚类分析与蚁群算法的混合启发式算法，通过算例分析，验证了模型的正确性及算法的有效性。研究成果对模糊需求下物资供应类装备保障点的选址-路径确定具有一定的参考价值。由于维修类装备保障通常采用分级多基地保障，备件库存状态转移相对稳定，多考虑基于马尔可夫过程的横向转运或延迟转运及备件库存模型。但文中的保障设施备选址评价方法对维修类保障设施的选址也具备一定的借鉴意义。