用GeoGebra绘制定质量理想气体的三维图像

乔永海

摘   要：文章解决了定质量理想气体状态方程的三维图像绘制问题，该图像是一个三维曲面，并在曲面上同时绘制了等容线、等压线和等温线，利于学生对该领域知识的深度学习。结合制作过程，又介绍了GeoGebra 软件的部分使用方法，利于该软件的推广使用。

关键词：理想气体;三维图像;GeoGebra ;教育技术;融合

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2020）8-0048-3

一定质量的理想气体状态方程和气体三大定律是高中物理热学的重点和难点部分，气体状态变化的图像能直观地表达气体的状态变化，涉及的有等温条件下压强随体积的变化，等容条件下压强随温度的变化，等压条件下体积随温度的变化等。有这样一个问题困扰着笔者：有没有压强、体积和温度的三维图像？从中学阶段产生这个疑问开始，总想试图解决这个问题，始终没能如愿。

认识到一款软件GeoGebra时，笔者便迫不及待地学习和使用，等熟悉了它的基本操作之后，成功解决了“绘制理想气体的三维图像”问题（如图1所示），制作过程十分简洁，现把经验分享给同行。

1    问题的提出

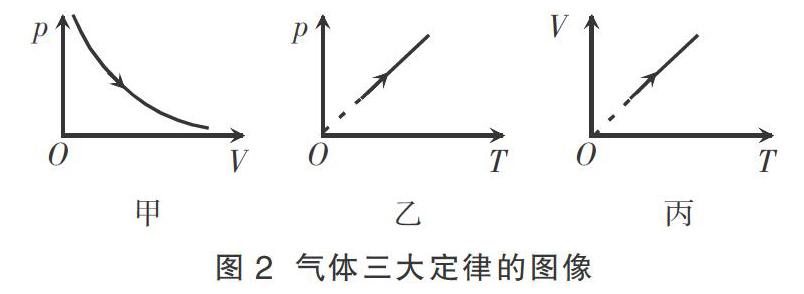
在学习气体的性质时，经常接触到图2所示的图像，其中甲图是一定质量理想气体的等温线，它是一条双曲线;乙图是一定质量理想气体的等容线，它是一条过原点的直线;丙图是一定质量理想气体的等压线，它也是一条过原点的直线。

甲                     乙                      丙

一定质量理想气体的等温线是一条曲线，另两条是直线，它们的差异实在太大了，能不能把这种不同用某种逻辑联系起来？这个问题是笔者中学阶段产生的疑问，教书期间也有学生问及类似问题。有没有一定质量理想气体的压强、体积和温度的三维图像？这个问题则是教书之后产生的疑问。

2    GeoGebra 软件简介

2002年数学教授Markus Hohenwarter 创建了动态教学软件GeoGebra，并通过开源的方式不断更新，众多的跨国团队共同开发，数百名翻译志愿者将其翻译成多国语言，包括汉语，因此GeoGebra的编程代码里可以用汉字。

GeoGebra 是为了从小学到大学各个学段的教学而设计的动态数学软件，功能强大、使用简单、交互性强，它将几何、代数、表格、作图、统计、微积分以直观的方式集于一身，既有平面作图，又有三维作图，相比其他三维软件，具有操作简洁和文件小的特点[1]。

数学是科学的基础，物理学是科学的组成部分，解决物理问题是离不开数学的，因此，这个软件是可以为物理所用的，就像当年的几何画板数学软件，在物理学领域的应用相当广泛[2]。

3    用GeoGebra绘制一定质量理想气体的三维图像

考虑到部分读者还不曾用过 GeoGebra，下面进行详细介绍，即使初次操作，按照本文的步骤也能制作出满意的作品来。

3.1    公式的变换

一定质量理想气体的状态方程的形式之一是：■=c（1）

为了和软件接轨，我们作如下假定和替换：

设c=1，x代替气体的体积V，y代替气体的温度T，z代替气体的压强p。

则（1）式变为：

■=1（2）

变形为：z=■（3）

也就是说，（3）式对应的在一定区间内的曲面就是我们寻找的理想气体的三维图像。气体的体积要大于零，x>0，表示温度的T不能小于零，也不能很接近零，所以y>2，这里都是相对值。

3.2    繪制3D图像

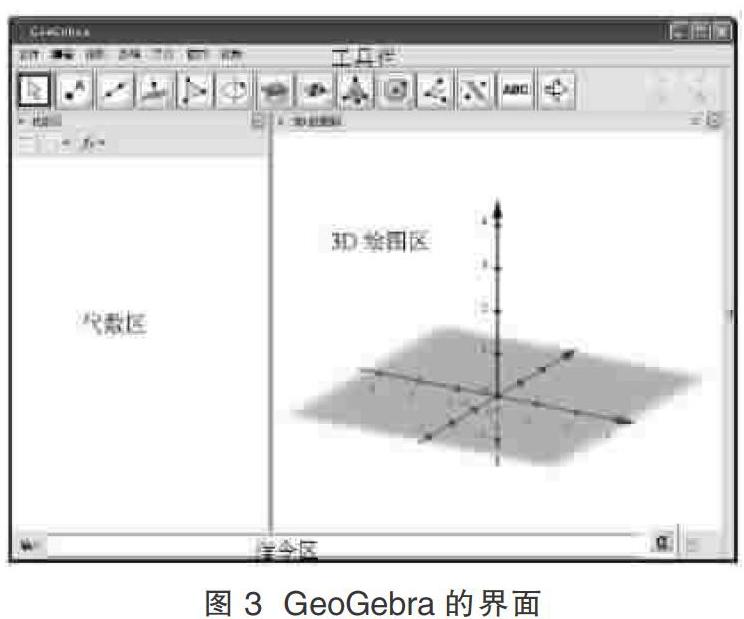
打开GeoGebra，选择“菜单栏”，勾选“代数区”“3D绘图区”“指令栏”，其他不勾选。如图3所示。

然后，在命令栏内输入代码：f（x，y）=如果[（x>0）∧（y>0），y/x]

提醒：代码输入的要求十分严格，要遵守编程的语法规则。除了汉字，其他字符必须在半角下输入，不能加空格，∧是逻辑符号“且”，不是键盘上的^，∧在命令栏右侧的a标志内选择。输入后把光标移到最后一个字符后面按“回车键”，就得到图像了（如图4）。如果回车后出现对话框，就说明输入有误，请重新输入一遍。一行代码解决了问题，十分便捷。

3.3    用不同的视图观察图像

首先，用“平移视图”工具（形状如图4左侧图示）把3D绘图区的坐标原点拖动到左下角。“平移视图”工具在工具栏最右侧工具的“抽屉”里，点击其右下方的小箭头，就可以找到。其他工具箱里也有很多工具，一定要选对。拖动后，点“移动”工具，进行下一步操作。“移动”工具就是最左侧的那个箭头样的工具（如图3）。提醒，选择一个非“移动”工具进行操作结束后，一定要点击“移动”工具，再进行旋转、选中等其他操作。

GeoGebra的操作按钮十分隐蔽，初学者不易找到。点击“移动”工具，再点击“3D绘图区”的空白区，点击该区左上角的三角箭头（图5中的3位置），出现一排按钮工具，可以分别试一试各个按钮的功能。最常用的是“旋转视图”按钮（图5中的1位置），点击后，图像转动，看到立体效果。“视图方向”（图5中的2位置）下面有4个按钮：xOy视图、xOz视图、yOz视图、旋转复位。这些工具十分有用。

图5中的一组双曲线就是等温线，可以看到不同温度下等温线的差异。经过V轴的斜线就是等容线，可以看到，在等容变化时，体积小等容线的斜率大。如何看到等压线呢？要做进一步的操作。

3.4    绘制等压线

选择“对象上的点”工具（如图3上部第2个工具箱内），点击z轴，建立一个可以沿着z轴移动的点，默认为A，右键进入“属性”窗口，在“常规”选项卡中更名为p。

然后，建立过p点的平行于VOT（xOy）的平面。在命令区输入：z=z（p）

然后，点击“相交曲线”工具（工具栏第7个），先后点击上述平面和曲面，得到两面的交线，这就是等压线。如图6所示，点击“移动”工具，拖动p点，可以看到等压线的变化。隐藏平面的操作是：点击平面按右键，不勾选“显示对象”。

如果选择xOy视图，就能够看到二维的等压线（如图7）。

4    小   结

经过以上操作得到了一定质量理想气体的压强、温度和体积变化的三维曲面图，如图6所示。在这张图上，我们可以看到，等温线、等压线和等容线是三维曲面图上面的曲（直）线。

我们绘制三维曲面图以及等温线、等压线和等容线，只用了两组代码，启用了几个工具，就得到了如此复杂的图形，足以感受到GeoGebra 操作的简洁性和功能的强大。

本文只是展示了GeoGebra的一个功能，其他的功能有待我们今后去开发，相信GeoGebra和物理教学的融合能对新课程改革发挥更大的积极作用。

参考文献：

[1]王贵军.GeoGebra与数学实验[M].北京：清华大学出版社，2017：1.

[2]明翔宇.巧用几何画板动态分析磁场“缩放圆”和“旋转圆”问题[J].物理教学探讨，2017，35（12）：52-54，58.

（栏目编辑    王柏庐）