“近朱者赤”：良好的同伴会产生正向影响吗？

杨 洲，黄 斌

2017年《全国教育事业发展统计公告》显示，我国初中阶段的毛入学率由2012年的102.1%上升到2017年的103.5%。虽然我国义务教育中的初中教育普及率显著提高，但是如何实现质的提升成为当务之急。2018年《政府工作报告》中明确提出“发展公平而有质量的教育”。2019年的中共中央、国务院出台了《深化教育教学改革全面提高义务教育质量的意见》明确提出“实施义务教育质量提升工程”等内容。随着我国经济发展水平的提高，对教育质量的追求将成为义务教育改革的重要方向。学业成绩作为衡量义务教育质量的重要指标，学生个人特征、家庭特征等因素均会对学生个体成绩产生显著影响。如孙志军等(2009)基于甘肃省20个县小学儿童数据分析发现，家庭背景等因素与儿童成绩有显著的正相关关系。就学生个体角度讲，个体的教育期望对学业成绩也会产生显著的正向影响(杨中超，2018)。

自《科尔曼报告》发布后，同伴对学生个体学业成绩的影响引起了社会的广泛关注。作为同伴效应的现实案例，孟母三迁的故事揭示了良好的同伴带来的积极作用。近年来，有关同伴效应的现象屡见不鲜，其中较为典型的例子便是“学霸宿舍”。围绕宿舍中出现的同伴效应现象，部分学者针对此类问题开展了相应研究。如梁耀明和何勤英(2017)利用新生入学宿舍随机分配这一自然实验，检验大学生学业成绩的宿舍同伴效应，结果表明学业成绩的宿舍同伴效应平均来看显著为正。随着相关数据的日益丰富，国内对同伴效应的研究领域不断延伸，如曹妍(2013)、武玮(2019)、Nicole(2015)、Brunello(2013)等考察了流动学生对本地学生学业成绩的影响，但是鲜有研究探讨玩伴和同学之间的同伴效应。因此，本文将利用中国教育追踪调查(CEPS)数据，探讨玩伴和同学之间的同伴效应对学生个体成绩的影响。

一、文献综述

根据“新人力资本理论”，人的能力可以划分为认知能力和非认知能力(李晓曼和曾湘泉，2012)。由于非认知能力在不同学科有着不同的定义，在计算非认知能力的影响时很难使用统一的指标。但认知能力的衡量标准可以采用数学成绩、阅读成绩等(Heckman and Kautz，2013)。已有研究表明，这些成绩会受到家庭社会资本、家庭经济资本等因素的影响。随着信息技术的发展，互联网会对学生的数学、英语、语文等成绩产生负作用(方超和黄斌，2018)。“同伴效应”的出现可以追溯到1966年科尔曼向国会递交的《科尔曼报告》。该报告指出，除了学生的家庭背景会影响学生的学业成绩外，周围同学的成绩、家庭背景等因素也会影响学生个人的成绩(Coleman,1966)。

Winston和Zimmerman(2003)发现学生的成绩不仅会受到家庭等方面的影响，还会受到来自舍友的影响。当SAT成绩处于中等水平的学生同处于后15%的学生同住一个寝室，那么处于中等水平的学生的成绩会下降。因此，同伴效应可以理解为个体行为不仅会受到自身的驱动，还会受到周围相似的主体的影响。传统的教育经济学则忽视了人与人之间的互动关系(叶星和熊伟，2017)，但实际情况是人与人之间的互动会影响人的行为，即近朱者赤，近墨者黑，这种互动关系对人的行为的影响开始得到了国内外学者的关注。在教育经济学中，同伴效应主要是指由个体所在学校和班级构成的同伴群体的学业成绩、能力、特征等会对其学业成绩以及个体行为等产生影响。这种影响有时是正向的，有时则表现出负面影响。如王春超和钟锦鹏(2018)通过开展小学生班级内随机排座实验发现学生之间存在同伴效应，且组内学生干部的同伴效应对于不同性别学生的影响存在显著差异，女性群体更受益于同伴效应。Anelli和Peri(2019)分析了30000名高中生在选择大学专业时是否存在同伴效应，结果显示男性群体和男性群体之间存在显著的同伴效应。赵颖(2019)使用CEPS数据研究了同伴效应对个体认知能力的影响，结果显示不断扩大的班级规模和学校规模将同伴效应的负面影响不断放大，且此种效应在不同群体之间存在差异。Lavy和Sand(2019)探讨了邻居和同班同学之间的同伴效应，结果表明同伴效应显著存在于拥有良好家庭社会资本的社会主体之间，且能显著减少暴力行为、增强合作意识以及提高课堂满意度。同伴效应不仅会因为学生的性别和家庭背景而有所差异，学生的个人能力也会影响同伴效应的作用。Feld等(2017)进行了大学生之间的同伴效应的研究，结果表明高能力的学生会表现得更好，而低能力的学生则表现得更差。可以看出，教育经济学中的同伴效应是一种内生的互动，即行为人的行为随着他所处的人群的行为而变化(陆铭和张爽，2007)。

同伴效应的关键问题是镜像问题，即是同伴影响了学生个体，还是学生个体影响了周围同伴。针对此问题，已有研究主要采用两种方法解决，一是随机试验，二是工具变量法(杜育红和袁玉芝，2016)。为了克服基准回归中的双向因果问题，已有研究较多使用工具变量法。如Case和Katz(1991)采同伴父母的平均行为作为工具变量克服镜像问题，Kang(2007)则采用同伴的其他学科成绩作为工具变量。其理由是在控制学校固定效应的条件下，如果不同科目任课教师质量等班级特定因素在这两门科目上相互独立，那么同伴的平均成绩和其他成绩就具有高度相关性(郑磊，2015)。

除了教育经济学领域，同伴效应还广泛应用于经济学领域。如曾江洪等(2019)研究高科技企业研发的同伴效应，江新峰和张敦力(2019)从影响企业投资同伴效应的角度考察了产业政策执行过程是否存在非经济因素干扰，李志生等(2018)研究了中国上市企业过度负债的地区同伴效应等。通过以上文献梳理可以看出，现有的关于同伴效应的研究日渐丰富。但是仔细分析发现既有研究仍为本研究的开展提供了研究空间。首先，现有的关于同伴效应的研究仍然较少。这主要是由于对“同伴”有着较为模糊的概念。如果将同伴仅仅固定在班级或者是学校层面，很容易忽视班级内群体对个体的影响。同时，这种划分方法又忽视了不在同一学校或同一班级的“同伴群体”对个体的影响。其次，普通基准回归会忽视由个体特征差异造成的结果偏误。随着义务教育阶段在校生规模的扩大，如果仅仅将拥有学习成绩优异的同伴群体的个体同其他个体相比较，可能会过高估计同伴效应的影响。

基于此，本文将“同伴”分为两类，一类是班级内除个体之外的其余学生。Albuquerque(2013)采用的是组织中个体特征相近的作为同群者。Dube等(2019)研究中以工人的工资波动区间为筛选依据，反映在本研究中是以学生成绩的波动区间为筛选依据。上述两种筛选方法均忽略了个体是否与筛选出的样本有着直接或者间接接触。如果按照阿尔伯克基的划分方法，很容易将非本校学生且与学生个体没有接触的样本纳入考察范围，导致高估同伴效应的影响。Mark和Roberts(2014)则将同群者界定为同一分组中，除个体之外的其余群体。因此，本文参考Mark和Roberts(2014)的划分方法，将同群者界定为同一班级中，除个体之外的其余学生。但是已有研究认为，同伴更像是“玩伴”，即同伴主要是以“生活”为导向，而非“学业”为导向(程诚等，2019)。因此，“同伴”的第二层含义是指学生个体的“玩伴”，此种玩伴可进一步区分为是否在同一班级。

二、模型设定与数据来源

(一)模型设定

参考已有研究，本文将按照线性均值的方法估计同伴效应对学生个体成绩的影响，公式为：

(1)

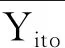
个体特征同群者的学业成绩是指排除学生个体P之外的同班同学的平均成绩。X代表一系列学生个体P的特征，本文选取性别、民族、是否具有随迁经历、是否生过大病、是否具有学业压力、是否住过院、父亲与母亲的受教育程度、家庭经济条件、是否为独生子女、家庭是否拥有计算机互联网等变量作为反映个体特征的变量。

已有研究指出，同伴效应的影响有可能是非线性的。例如Ding和Lehrer(2007)指出混合分班有助于促进成绩较差的学生的学业成绩的提高，而成绩较好的学生则受益于按成绩分班。Lai(2007)的研究发现，同班同学成绩的平方与标准差与个体学业成绩具有明显相关性，该结果表明同班同学的多样性有助于提高学生学业成绩。基于此，本文进一步讨论同班同学与学生个体成绩的非线性关系，参考已有研究，选取公式：

(2)

良好的人际交往也是同伴效应的界定方法。据此，本文还将玩伴的学习好坏作为切入点，探究同伴效应的影响。具体来看，CEPS数据中涉及“好朋友学习成绩是否优良”，答案涉及三个选项：“没有这样的”“一到两个这样的”“很多这样的”，本文将据此构建二元变量，即“好朋友学习成绩优异”为1，否则为0。具体来看，将“很多这样的”赋值为1，其余0。如果将答案中“一到两个这样的”赋值为1，很有可能扩大同伴效应的影响。鉴于此，本文只将第三个答案，即“很多这样的”赋值为1。接下来，本文将采用倾向得分匹配法进一步估计同伴效应的平均处理效应，公式为：

ATT=E{E|Score1p-Socre0p|Dp=1,g=P(Xp)}

(3)

上式中，Score代表代表有无拥有学业成绩优异的同伴群体的学生个体P的学业成绩，D是二元虚拟变量，即同伴学习成绩是否优异。g为学生个体P拥有学业成绩优异的同伴群体的概率值。

(二)数据说明

本文采用的是中国人民大学开展的2013—2014年的CEPS数据，调查对象为全国抽取的28个县级单位的112所学校中的438个班级。该数据优势在于调查对象为随机抽取，大部分调查学校为采用随机分班的方式，这种随机试验对于识别同伴效应具有重要意义。剔除缺失值数据后，将11074名学生作为分析样本。为了克服同伴效应中的镜像问题，筛选出50个按照随机方式分班的学校，且筛选出的样本在八年级时未出现再分班现象。本研究在利用OLS回归时，将以这50个学校为分析对象，探讨同伴效应对学生个体成绩的影响。

父母受教育情况、家庭情况以及是否独生子女构成了学生个体的家庭变量。其中对父母受教育情况构造成以“是否接受过高等教育”的二元虚拟变量，接受过高等教育取值为1，否则为0。家庭经济情况分为非常困难、比较困难、中等、比较富裕和很富裕五个类别，当家庭经济情况处于中等及以上时，取值为1，其余为0。性别、民族、是否具有随迁经历、是否生过大病以及是否住过院构成学生个体特征变量。本文将原问卷中“几岁时来到本县”构造成“是否具有随迁经历”的二元虚拟变量，如果自出生时就在本县，取值为0，否则为1。另外，班主任的学历情况、职称以及学校类型也会对学生成绩产生影响。选取班主任是否具有研究生及以上学历、是否具有高级职称以及学校是否属于公立院校探讨班级以及学校对学生成绩的影响。

表1中的前三行是本文的因变量。其中处理组是指拥有学业成绩优异的同伴群体的学生群体，这部分学生群体的语文、数学以及英语成绩均值为72.030、71.993和72.132。控制组是指拥有学业成绩较差的同伴群体的学生群体，语文、数学以及英语成绩标准化后的均值为69.982、69.740和69.732。可以看出，处理组的学业成绩均值均高于控制组，但这种差距是否来源于同伴效应有待证明。

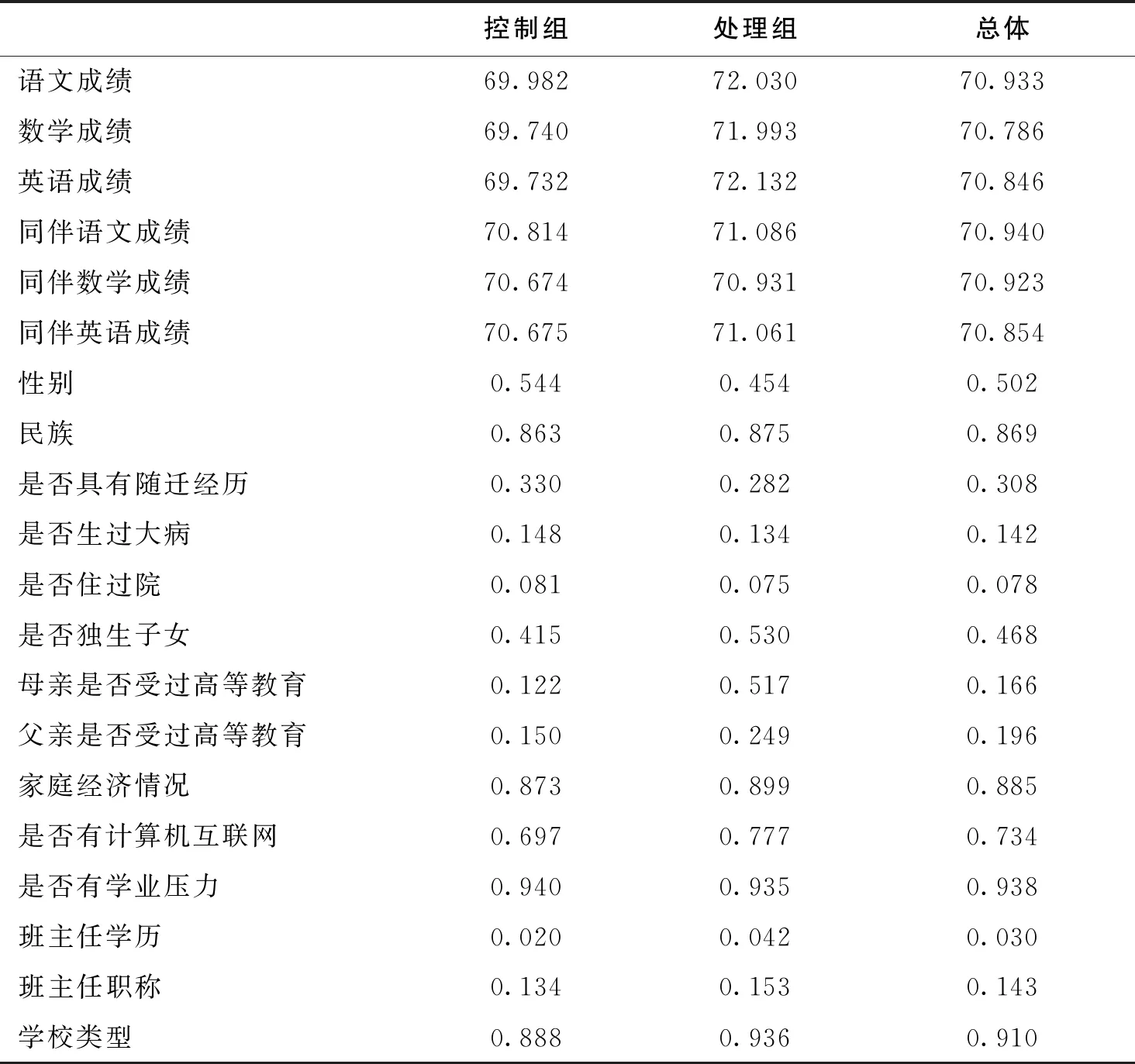
表1 各变量的均值

三、实证结果

(一)班级内的“同伴效应”

表2列出了基本回归结果。可以看出，同伴效应对学生的语文、数学以及英语等学科成绩均有正向影响。这说明班级内其他同学的成绩能够对某个学生产生影响。同伴效应的产生主要有两方面原因，一是学生之间的“从众效应”，二是学生之间的互动交流。就“从众效应”讲，学生入学时是采取随机的方式进行分班，学生能力层次不齐。当学生个体发现周围同学在努力学习时，会激发学生个体的学习动机，最终触发共同学习行为。正如“学霸宿舍”等现象，可以认为是“从众效应”的现实表现。另一方面，学生之间的互动交流是同伴效应的重要作用机制(Feld和Zölitz，2017)。就中等能力的学生而言，与成绩更好的同学互动有可能促使其成绩提高，但是与成绩较差的同学互动也有可能使其成绩下降。已有研究表明，当中等能力学生与成绩更差的同学互动容易降低其成绩，同时，学习成绩较差的同学与自己同一水平的学生互动则会更差(赵颖，2019)。

其他变量中，是否住过院对语文、数学和英语成绩会产生负面影响，这与实际情况相符，即良好的健康条件会对学业成绩产生正向影响。是否拥有计算机互联网对语文、数学、英语等三科成绩也具有负面影响，这主要有两方面原因。一是计算机互联网的普及虽然方便了学生学习，但处于七年级和九年级阶段的学生由于自控能力正在发育，使得计算机互联网的娱乐效用超过了学习效用。此外，计算机互联网的使用占用了学生的学习时间，从而影响了学业成绩。另一方面，计算机的使用日益普遍，“打字”代替了“写字”，提笔忘字的现象屡见不鲜，尤其是对于正处于学习阶段的学生。父母是否接受高等教育对于学生的学业成绩会产生正向影响，这与预期的相符。已有研究表明，父母的受教育程度越高，越能在学业上给予子女更多的帮助(李佳丽和何瑞珠，2019)。但是家庭经济情况对数学和英语成绩没有显著影响，对语文成绩却有显著的正向影响。这是由于经济较为富裕的家庭往往拥有良好的家庭氛围，从而对子女的表达能力、语言分析等方面产生正向影响。

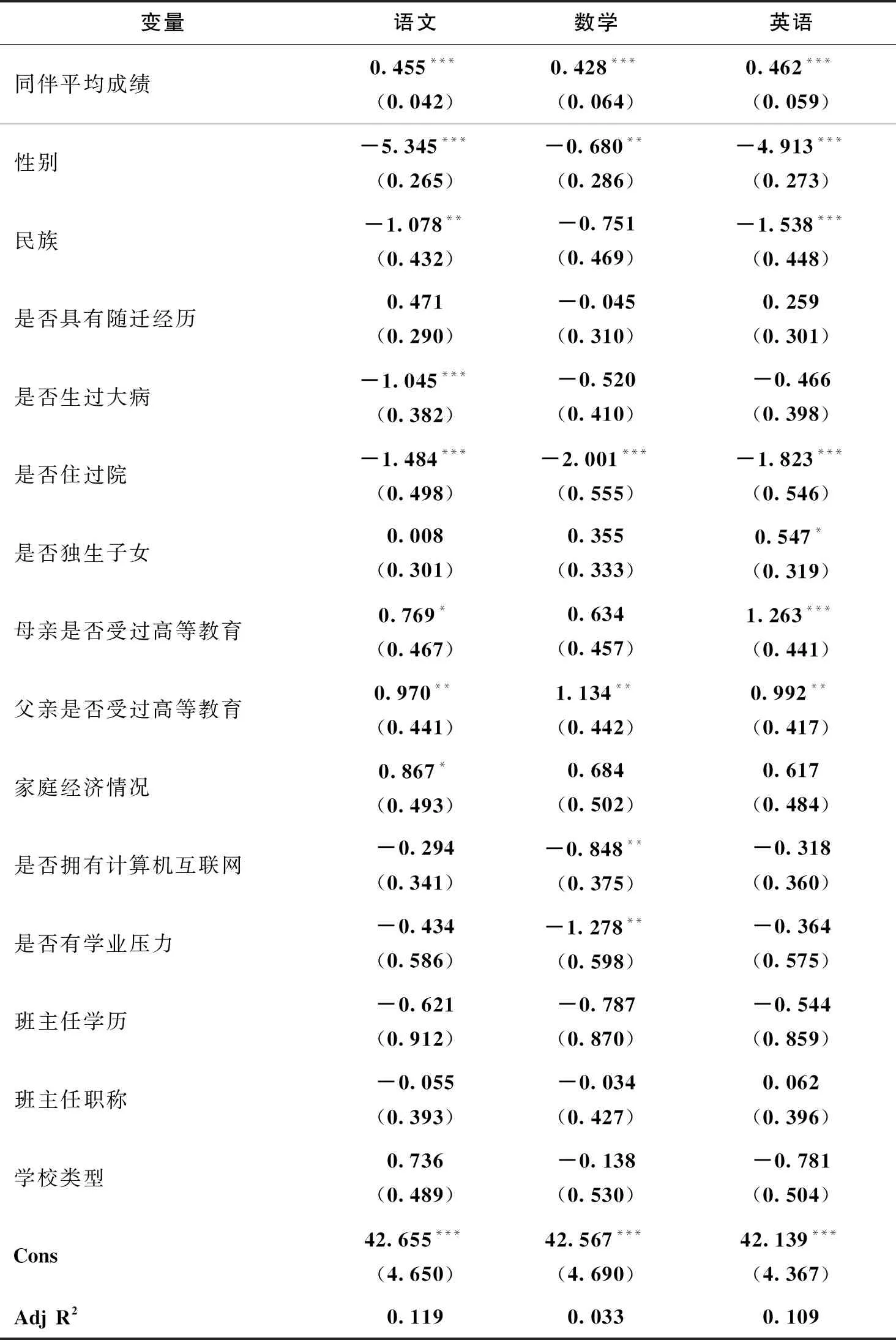
表2 回归结果

通过表3可以看出，学业成绩的平方项对学生个体成绩的影响为正，且在1%水平上显著，说明初中生的同伴效应中存在显著的、正向的、非线性关系。这说明学生个体成绩会随着同班同学成绩的提高而降低。但到达某一拐点时，同班同学成绩的提高会对学生个体成绩产生正向影响。同时，同班同学成绩的方差对学生个体成绩具有负影响，但是未通过显著性检验，这说明存在班级其他同学成绩的离散程度较低可能有助于提高学生个体成绩。但是如果将同质性能力的学生分在相同班级，有可能形成“马太效应”，即学业成绩好的学生会越来越好，学业成绩较差的学生成绩越来越差。

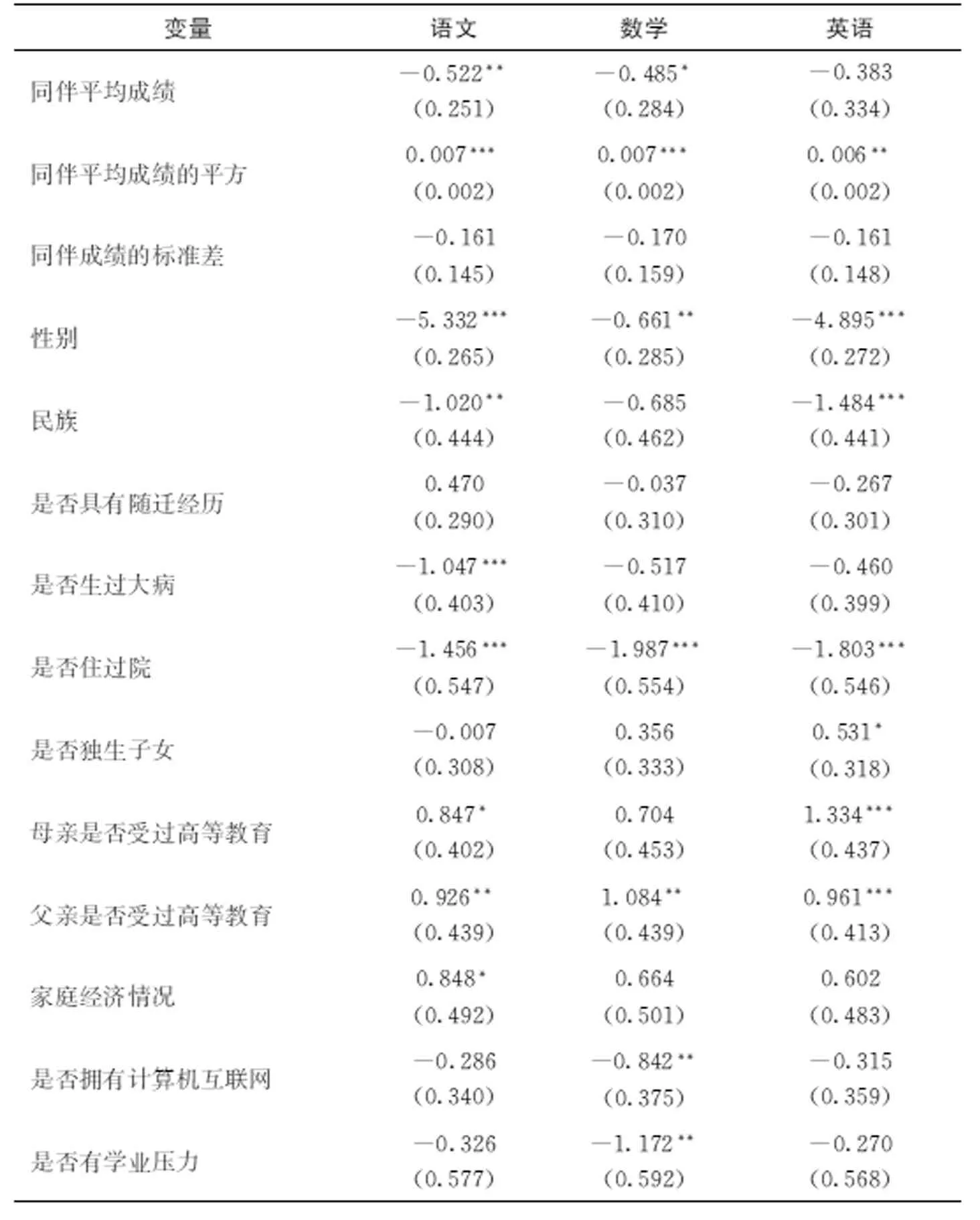
表3 非线性回归结果

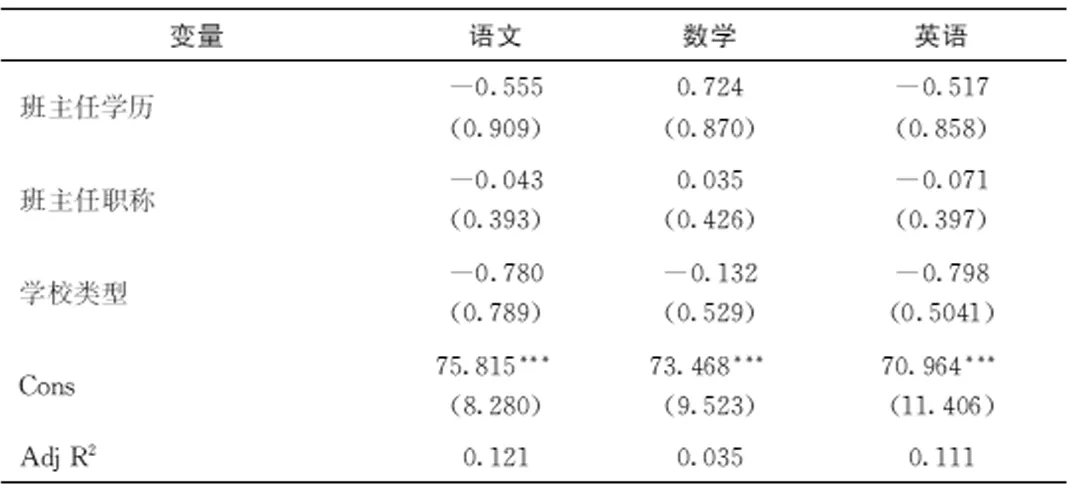
续表

(二)玩伴之间的 “同伴效应”

在进行倾向得分匹配之前对各协变量进行了平衡性检验，结果如图1和表4所示。根据表4可知，各协变量的标准偏差绝对值均有不同程度下降。其中“家庭经济状况”变量的偏差下降了100%，其余变量的偏差的降幅也在10%以上。除“是否生过大病”外，其余各协变量的t值在匹配后均小于临界值1.96，p值大于0.1，说明匹配后的处理组和控制组不存在显著差异。同时，匹配后的处理组与对照组之间标准化偏差小于20%，说明匹配成功。其次，对伪R2、卡方、偏差均值、B值和R值的分析表明匹配也较为成功。具体来看，匹配后伪R2、卡方、偏差均值、B值和R值均有所下降，且B小于25%，R在0.5-2范围内即可认为满足匹配平衡性假定条件(Rubin,2001)。如表5所示，匹配后的B值为9.8%，R为1.17均在可接受范围内。

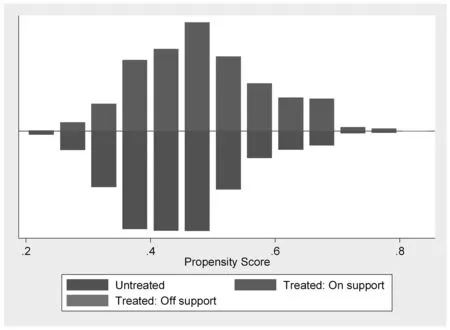
图1 倾向得分匹配法共同取值范围

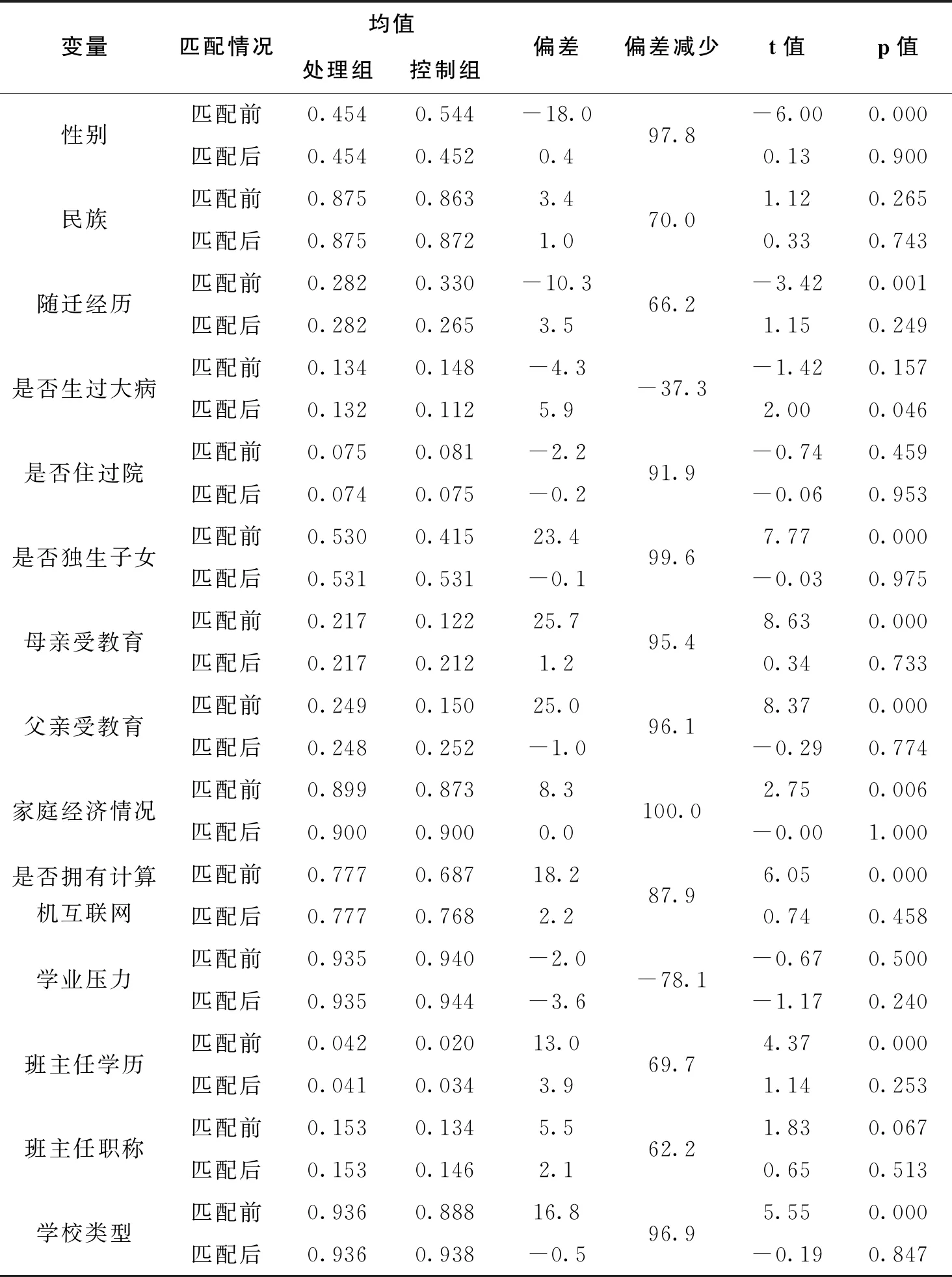
表4 各变量的平衡性检验

表5 匹配平衡性假定检验结果

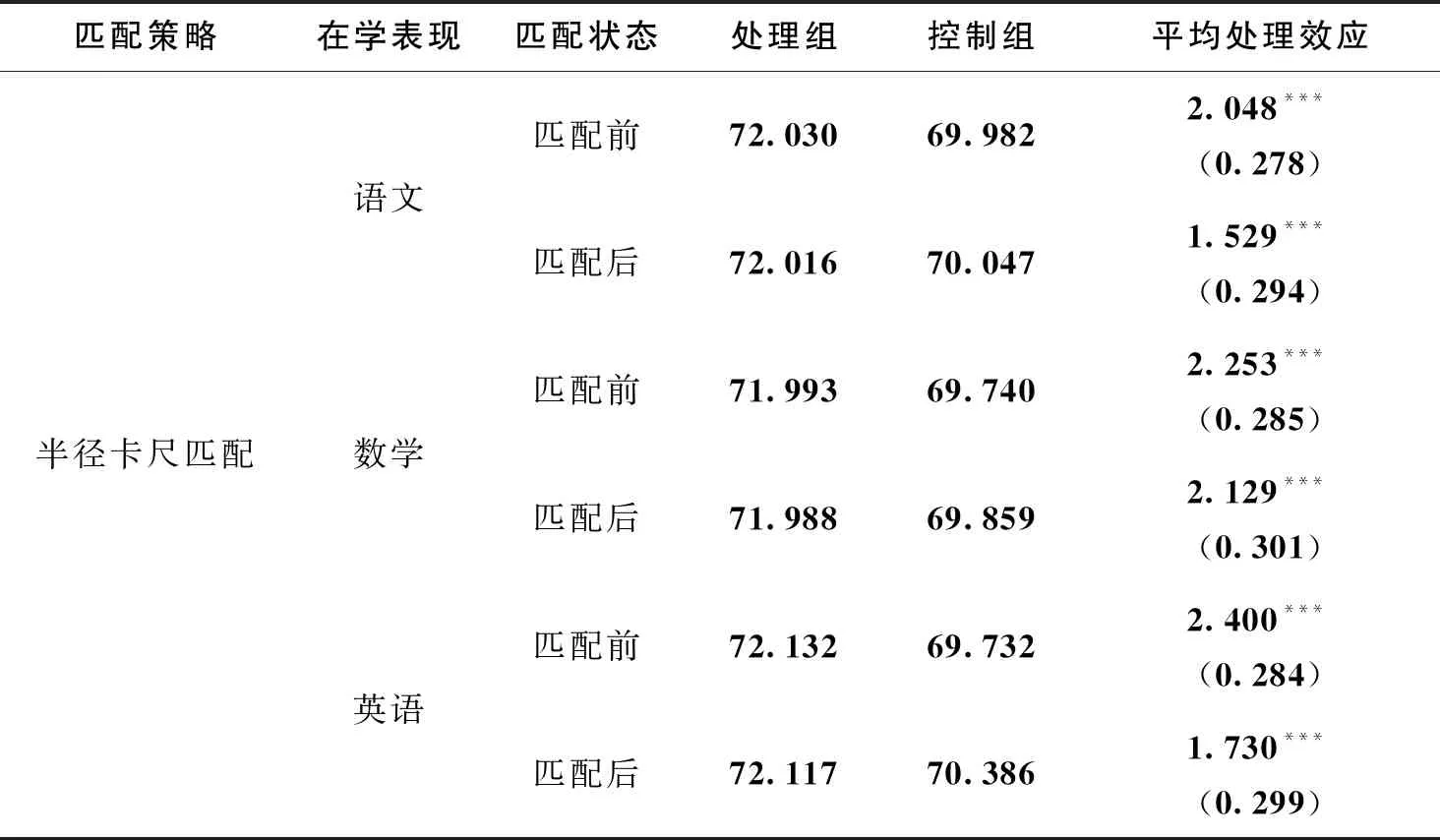
本文利用近邻匹配、核匹配以及半径卡尺匹配估计同伴效应的影响，结果如表6所示。在K=1的近邻匹配中，匹配前的处理组，即拥有学习成绩优异的学生个体的语文、数学以及英语成绩为72.030、71.993、72.132，控制组的三科成绩为69.982、69.740、69.732，处理组与控制组之间相差2.048、2.253、2.400。匹配后，处理组的语文、数学、英语成绩为72.016、71.988、72.117，控制组的三科成绩为70.415、69.893、70.336，处理组与控制组之间相差1.602、2.094、1.781。三科成绩的处理组与控制组之差均有所减小，说明倾向得分匹配法减少了由于选择性偏误和反事实偏误带来的结果偏差。

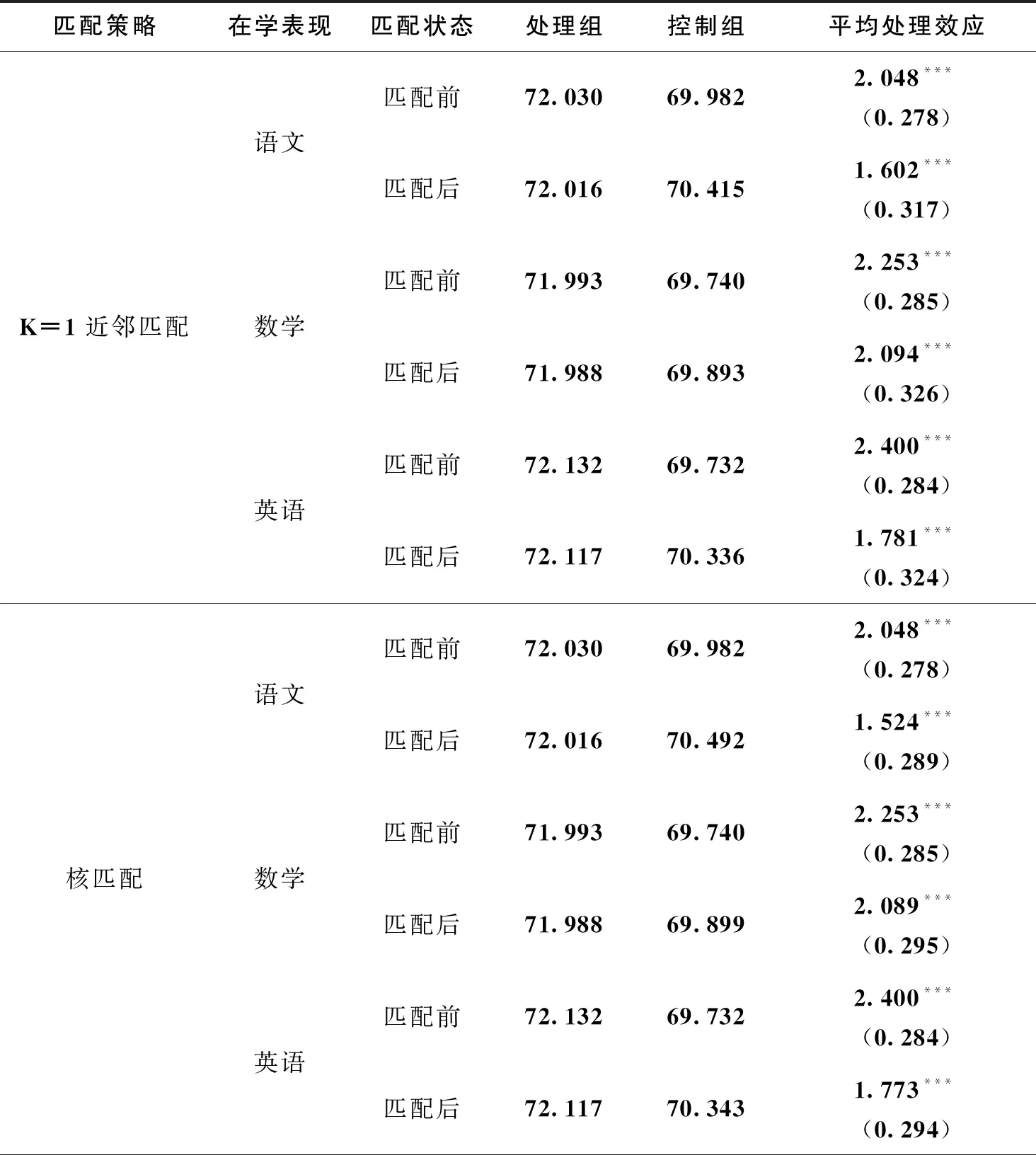
表6 同伴效应的匹配结果

续表

从结果来看，无论是匹配前还是匹配后，拥有学习成绩优异的同伴群体的学生个体的成绩显著高于其他群体的学习成绩，再次证明同伴效应的存在。就学科而言，同伴效应对不同学科的影响力由大到小依次为数学、英语和语文。这主要是因为学科性质的不同。数学学习主要依赖逻辑推演与计算能力，学生个体很容易受到同群者解题思路的影响。尤其是当同群者具有扎实的数学基础时，良好的解题思路会引起周围同学的效仿。但是语文和英语的学习主要强调知识的积累，尤其是语文的学习无法通过知识的外溢而影响其他学生。相较于语文学习，良好的英语学习方法则可以通过交流、答疑等途径实现知识的外溢。核匹配和半径卡尺匹配与近邻匹配得到的结果相近，匹配后的同伴效应对数学成绩影响最显著，英语次之，对语文成绩影响最小，验证了本文结果的稳健性。

(三)班级内玩伴之间的“同伴效应”

进一步筛选出好友与学生个体在同一班级的样本，表7为筛选之后的匹配结果。匹配方法仍旧是采取近邻匹配、核匹配和半径卡尺匹配。可以看出，无论采取何种匹配方法，结果与表6相同，即拥有学习成绩优异的同伴群体的学生个体的成绩显著高于其他群体的学习成绩。总体来看，匹配前的处理组和控制组的差距要大于匹配后处理组与控制组之差，这主要是因为单纯地比较拥有学习成绩优异的同伴群体的学生学业成绩忽视了学生个体之间的差异。换句话说，直接将拥有学习成绩优异的同伴群体的学生学业成绩进行对比高估了同伴效应的影响。具体来看，拥有学业成绩优异的同伴群体的学生，其数学成绩受到的影响最大。相较于其他同学，其数学成绩要高出1.918-2.141分，语文成绩高出1.383-1.444分，而英语成绩高出1.439-1.768分。

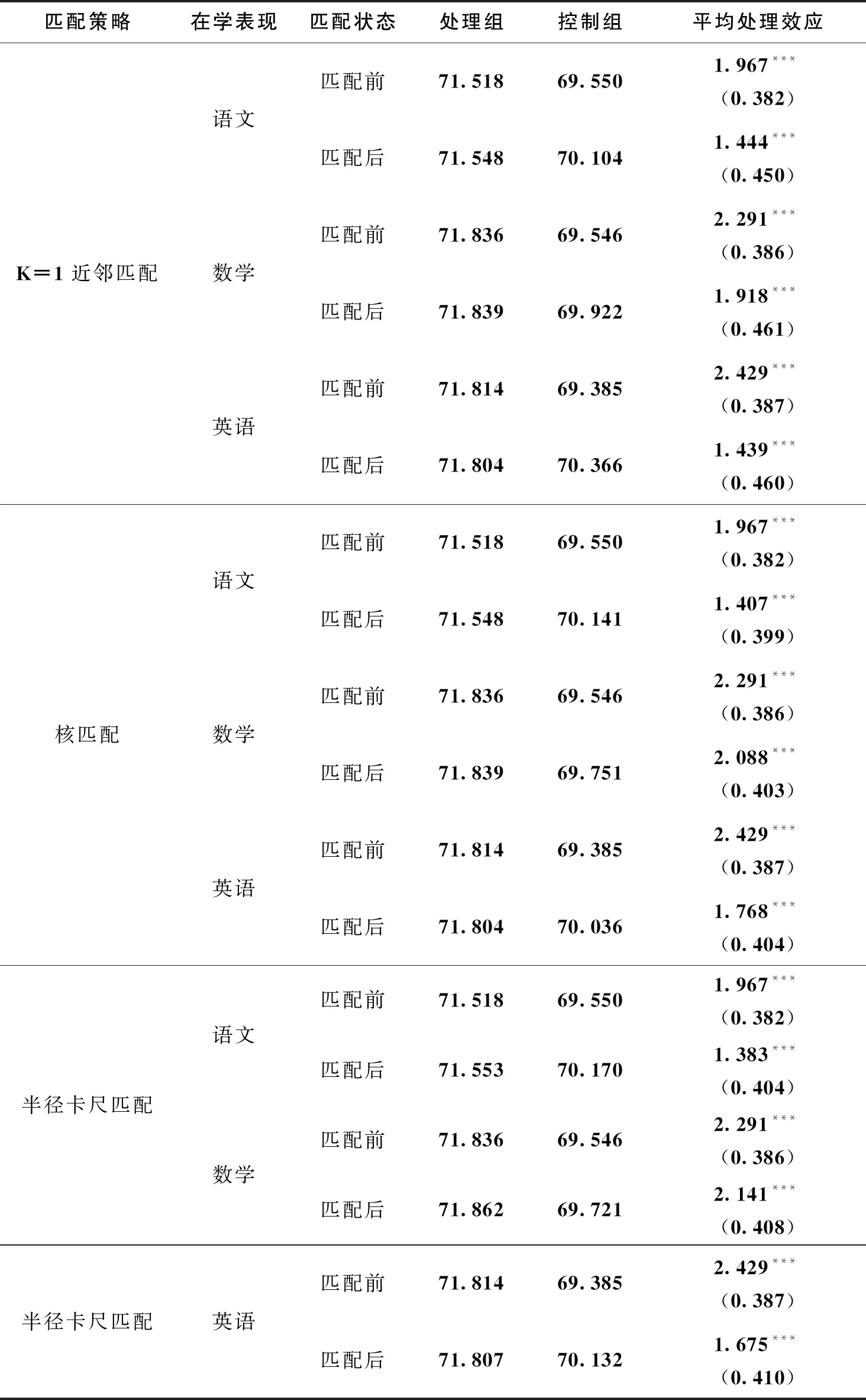
表7 同伴效应的匹配结果

四、结论与建议

本文利用2013—2014年“中国教育追踪调查”基线数据，探讨了同伴效应对学生个体学业成绩的影响。研究结论如下：首先，同伴效应对学生个体成绩有正向影响。其中同伴效应对学生个体的英语成绩影响最大，同班同学成绩每提高10分，学生个体成绩将会提高4.62分。对数学成绩影响最小，同伴同学的数学成绩每提高10分，学生个体的数学成绩将提高4.28分。其次，加入同伴成绩的平方项和方差以探讨同伴效应的非线性影响。结果表明同伴效应中存在显著的、正向的、非线性关系。这说明同伴影响为凹性关系。同时，同班同学成绩的方差对学生个体成绩产生负向影响，但未通过显著性检验，这说明有可能存在班级学生能力的异质性不利于提高个体学业成绩的情况。再次，采用倾向得分匹配法探讨同伴效应的影响。结果显示无论是匹配前还是匹配后，拥有学习成绩优异的同伴群体的学生个体的成绩显著高于其他群体的学习成绩，再次证明同伴效应的存在。就学科而言，同伴效应对不同学科的影响力由大到小依次为数学、英语和语文。最后，进一步筛选出同伴在相同班级的样本，结果显示拥有学习成绩优异的同伴群体的学生个体的成绩显著高于其他群体的学习成绩。

针对以上结论，本文提出两点建议：

一是取消重点班的设置。《义务教育法》第22条规定:“县级以上政府及其教育行政部门不得将学校分为重点学校和非重点学校，学校不得分设重点班和非重点班。”教育部也曾多次发文，要求各地禁止在义务教育阶段设立重点班，确保义务教育公平。目前越来越多的地方行政主管部门和教育主管部门发布取消重点班的设置，逐步实现义务教育均等化。根据本文的结论，降低班级同学成绩的离散程度会提高学生个体成绩，但同班同学成绩与学生个体成绩也存在“U”型关系。在达到某一拐点时，同班同学成绩的提升会对学生个体成绩产生正向影响。另一方面，重点班往往是将高能力或者成绩较高的学生聚集在同一班级，此种分班方式虽然有助于进一步提高成绩良好的学生的成绩，但是却忽视了高能力组的学生与低能力组学生之间的潜在负面效应(赵颖，2019)。

二是实行随机派位分班政策。随机派位是指通过抽签系统随机分入指定学校的方式，顾名思义，随机派位分班是指通过抽签系统将学生随机分班。目前，我国仍有部分学校采取入学考试的形式进行分班。如本文所使用的CEPS数据中，16所学校未采取随机分班政策。本文结论认为学生个体和同伴成绩之间存在显著凹性关系。按照随机派位的方式分班可以保证班级内学生能力和成绩的异质性，同时将高能力和低能力的学生聚集在同一班级兼具效率价值。

但是本文并没有讨论同伴群体异质性达到何种水平有利于学生成绩的提高，这是本文的不足之处。同时，本文也尚未考虑班级规模对学生学业成绩的影响。为了保证学生可以享受到公平、优质的义务教育，我国出台了多项政策取消大班制。但是，班级规模达到何种水平会对学生的学业成绩产生正向影响也是本文尚未解决的问题。