基于旅游线路规划的蚁群优化算法研究

李磊 张延星 谢超

摘  要： 传统的乡村旅游线路规划方法存在进化速度慢的缺点，导致搜索速度慢，为此提出一种基于蚁群优化算法的乡村旅游线路规划方法。在建立蚁群优化算法模型的基础上，针对拥堵状态和非拥堵状态分别优化信息素更新策略，对最优线路求解，完成基于蚁群优化算法的乡村旅游线路规划方法的设计。通过对比实验，与模拟退火算法、基本蚁群算法作比较。实验结果表明，提出的蚁群优化算法因在每次迭代中优化信息素更新策略，明显提高了搜索速度，且缓解了景点拥堵情况。

关键词： 蚁群优化算法; 旅游线路规划; 信息素更新; 线路规划模型; 旅游线路设计; 最优路径

中图分类号： TN911.1?34; TP311                     文献标识码： A                  文章编号： 1004?373X（2020）17?0115?04

Abstract： The traditional rural tourism route planning method has the disadvantage of slow evolution speed， which leads to slow search speed. Therefore， a rural tourism route planning method based on ant colony optimization algorithm is proposed. The model of ant colony optimization algorithm is established. On the basis of the model， the pheromone update strategy is optimized for dealing with both the congestion state and non?congestion state， and the optimal route is solved， so as to complete the design of rural tourism route planning method based on ant colony optimization algorithm. The proposed method is compared with simulated annealing algorithm and basic ant colony algorithm in the comparative experiments. The results show that the ant colony optimization algorithm proposed in this paper can obviously raise the search speed and alleviate the congestion of scenic spots because the pheromone update strategy is optimized in each iteration.

Keywords： ant colony optimization algorithm; tourism route planning; pheromone update; route planning model; tourism route design; optimal path

0  引  言

隨着人们生活水平的提高，越来越多的人选择旅游作为放松方式之一，旅游产业随之得到了发展。旅游产业不仅可以加速区域之间的资金流转，还可以创造高效的消费模式，带动周边地区的经济发展[1]。为带动农村经济发展，国家大力支持乡村文化旅游产业，针对乡村旅游线路规划问题开展研究，对于促进乡村旅游的发展十分重要。现有的旅游线路规划方法仍然存在所得线路非最优、搜索时间长的缺点，需要对其作进一步研究[2]。在旅游线路规划的研究中，为寻找最优线路，很多研究者均采用蚁群算法。然而，蚁群算法存在搜索时间长、易于停滞的缺点，需要对其作进一步优化[3]。近年来，蚁群优化算法被广泛应用在各个领域中，很好地改进了蚁群算法的不足[4]。基于上述分析，本文提出一种基于蚁群优化算法的乡村旅游线路规划方法，并通过对比实验验证了提出的蚁群优化算法具有更快的搜索速度。

1  基于蚁群优化算法的乡村旅游线路规划方法

1.1  建立蚁群优化算法模型

蚁群算法是一种用来寻找优化路径的概率型算法。这种算法具有分布计算、信息正反馈和启发式搜索的特征，本质上是进化算法中的一种启发式全局优化算法[5]。蚁群寻优示意图如图1所示。

由图1可知，从巢穴到食物之间，蚁群通过消息互通寻找到共同认可的最短路径。蚁群算法的优势在于搜索过程采用分布式计算方式，多个个体同时进行并行计算，大大提高了算法的计算能力和运行效率。所以利用蚁群优化算法建立旅游线路规划模型。

式中：[tabuaa=1，2，…，m]代表蚂蚁[a]历经景点的集合;[ηij]代表蚂蚁从景点[i]向景点[j]移动的期望值，是一种启发式函数，[ηij=1/dij];[α]代表景点之间路径上信息素的重要程度，其值越大，则表明信息素产生的影响越大[6];[β]代表景点间距离的启发函数的重要程度，其值越大，则表明其产生的影响越大。

为了描述蚂蚁在历经景点时信息素的挥发状态，通过挥发因子[ρ]对路径信息作调整，当所有蚂蚁完成一次完整的景点走访后，更新所有景点之间信息素的值，通过式（2）实现：

式中：[1-ρ]代表信息素的剩余调整程度值;[Δτaij]代表第[a]只蚂蚁完成本次访问后，在景点[i]和景点[j]之间分泌出的信息素的增加量;[Δτij]代表全部蚂蚁在完成本次访问后，在景点[i]和景点[j]之间分泌出的总信息素的浓度。其中，[Δτaij]的计算公式如下：

通过上述内容，完成蚁群优化算法模型的建立。

1.2  优化信息素更新策略

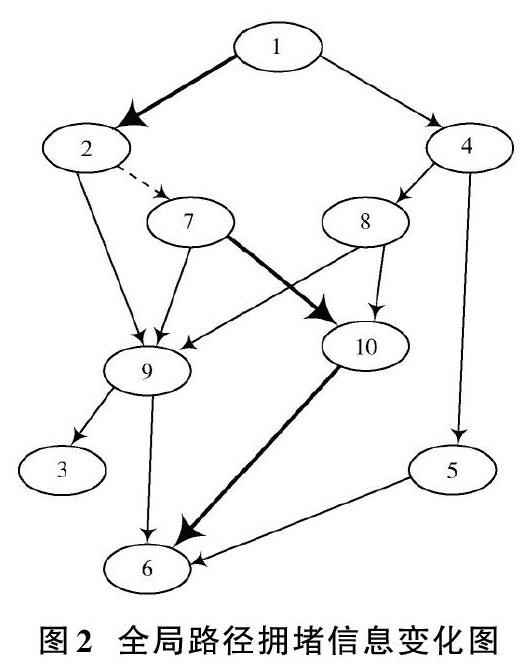
蚁群算法在初始化时，每条路径上信息素的量值是相同的[7]。在算法初期，蚂蚁以相等的状态转移概率选择路径。考虑拥堵因素后，如果每条路径的信息素量值相同，会降低蚂蚁寻找最优路径的效率，增加寻求最优解的时间[8]。因此，需要对信息素的更新策略作优化。对于全部路径来说，交通信息时刻都在变化。最优路径上可能存在拥堵状况，其他路径可能会从拥堵变成畅通的状况，如图2所示。

在图2中，虚线表示拥堵路段。从景点1到景点6的最优路径为[1→2→7→10→6]，其中，[2→7]路段突然变成拥堵状态。此时，原来的最优路径已经不再是最优选择，则信息素会更新策略，重新选择交通畅通的路径[9?12]。通过限定各条路径上的信息素强度，使每两个景点之间路径上的信息素强度保持在稳定的范围内，并使信息素强度尽可能集中在较优路径上，使其最终可以找到全局最优解。

当无拥堵状况时，对信息素更新策略的具体内容如下：当所有蚂蚁完成一次走访后，从中随机选择一只蚂蚁的走访路径[Lk]的长度作为标准，将其他蚂蚁的走访路径[Lj]的长度与该条路径长度作比较，更新[Lk]的信息素，以及比该路径更短的路径上的信息素浓度，以便最后所得最优解为全局最优解而非局部最优解。

1.3  最优线路求解

在优化信息素更新策略后，求解最优线路，具体实现步骤如下：

初始化：将信息素[τij]的值初始化设为1，启发式信息在迭代过程中保持不变;

构造解：随机选择一个景点作为蚂蚁[a]的出发景点，从景点出发并历经所有景点，假设蚂蚁[a]还没有走访完全部景点，则从蚂蚁[a]当前的位置开始，随机选择下一个景点。当还有没走访到的景点时，随机产生一个（0，1）之间的随机数，如果随机数小于控制参数，则从未走访到的景点中，选择有最大可行性的景点作为下一个要历经的景点，否则以轮盘赌的方式选出下一个走访景点。如果蚂蚁在历经完全部景点后，则返回历经景点的先后顺序。蚂蚁遍历景点的具体步骤如图3所示。

在蚂蚁遍历景点的过程中，采用轮盘赌的方式[13?15]，通过每个蚂蚁个体的选择概率计算出累积概率，再通过随机产生的随机数，与累积概率作比较，决定下一个要选择的景点，通过不断地迭代直到找到最短线路，将其输出。

至此，完成基于蚁群优化算法的乡村旅游线路规划方法的设计。

2  仿真实验与分析

为验证此次提出方法的有效性，采用提出的基于蚁群优化算法的乡村旅游线路规划方法，以河北某地区旅游乡村为例，对其旅游线路展开规划，并与基本蚁群算法、模拟退火算法的乡村旅游线路规划方法作对比。

2.1  实验环境

搭建实验环境，通过Matlab平台进行仿真实验，实验环境参数设置如表1所示。

在上述实验环境下，对该地区的乡村旅游景点排序，分别为1～10。设置信息素量值的最小值为10，最大值为1 000。景点的位置分布如图4所示。

2.2  旅游景点全局拥堵

为验证提出方法的路径规划性能，以景点拥堵情况为实验指标，采用提出的基于蚁群优化算法、模拟退火算法及基本蚁群算法的线路规划方法，对上述10个旅游景点展开规划。基于上述实验环境进行仿真实验，记录旅游高峰时间段10：00—14：00景点的拥堵情况，得到的实验结果如图5所示。

由图5可知：利用模拟退火算法与基本蚁群算法规划后的景点拥堵情况未得到较好地缓解，尤其是必经景点1，4，5，6的拥堵较为严重;而利用提出的蚁群优化算法规划后的景点拥堵情况有所缓解，各景点的游客负载量较为均衡。因为提出算法考虑了拥堵因素，如果每条路径的信息素量值相同，会降低蚂蚁寻找最优路径的效率，对信息素的更新策略进行了优化，缓解了高峰时间段景点拥堵的情况。

2.3  算法进化速度

為验证提出方法在进化速度的性能，设计实验验证蚁群优化算法、基本蚁群算法和模拟退火算法执行过程中的进化速度（搜索速度）。算法的收敛速度越快，搜索速度越快，说明进化速度性能越好。对比结果如图6所示。

从图6中可以看出：模拟退火算法在第198次开始收敛，达到最优;基本蚁群算法在第169次开始收敛到最优;而提出的蚁群优化算法在第100次收敛到最优。通过对比发现，提出的蚁群优化算法通过在每次进化过程中更新信息素策略，极大地提高了算法找到更优解的概率，提高了进化速度，从而使搜索时间加快，具有更好的全局搜索能力。

3  结  语

针对传统的乡村旅游线路规划算法存在的进化速度慢而导致搜索时间长的缺点，本文设计了基于蚁群优化算法的乡村旅游线路规划方法。通过对比实验，与基本蚁群算法和模拟退火算法作比较，实验结果证明了提出的蚁群优化算法具有更快的搜索速度，缓解了景点拥堵情况。希望本次研究可以为乡村旅游线路规划及其他优化研究提供一定的参考价值。

参考文献

[1] 赵希勇，张璐，吴鸿燕，等.哈尔滨地区乡村旅游资源评价与开发潜力研究[J].中国农业资源与区划，2019，40（5）：180?187.

[2] 余瑞林，陈慧媛，陈广平，等.湖北省乡村旅游地空间分布及其影响因素：以高星级农家乐为例[J].经济地理，2018，38（6）：210?217.

[3] 唐瑞雪，高鹏，王凯，等.青城山旅游区观光车运营规划研究[J].交通运输工程与信息学报，2018，16（2）：131?135.

[4] 周啸，李少梅，王旭，等.兴趣旅游地理信息服务系统设计与实现[J].测绘工程，2018，27（5）：46?51.

[5] 罗劲文.西安市跨坐式单轨旅游示范线线路方案比选[J].城市轨道交通研究，2018，21（6）：66?70.

[6] 郭伟，薛耀文.不同对接条件下的旅游线路设计研究：以临汾市为例[J].山西师范大学学报（自然科学版），2019，33（2）：50?57.

[7] 那守海，徐兆敏，赵希勇.“反规划”视角下的湿地旅游规划控制指标体系研究[J].中国农业资源与区划，2018，39（11）：219?224.

[8] 李强.长治市太行山大峡谷旅游轨道交通布局规划研究[J].铁道运输与经济，2019，41（3）：80?84.

[9] 冯立新，王杏，梁兀铭.中国风景道规划设计创新点及创新本源探究[J].云南地理环境研究，2017，29（5）：38?43.

[10] 朱明，史春云.长三角旅游线路空间模式的动态演变：基于2010，2016年数据的比较研究[J].江苏师范大学学报（自然科学版），2018，36（1）：71?74.

[11] 杨临涧，赵祥模，贺冰花，等.随机用户均衡交通分配问题的蚁群优化算法[J].交通运输工程学报，2018，18（3）：189?198.

[12] 王海鹰，秦奋，张新长，等.基于蚁群优化算法的城市生态用地空间规划模型[J].地理科学，2017，37（3）：426?436.

[13] 史先鹏，解方宇，张波涛.一种基于改进蚁群优化算法的载人潜水器全局路径规划[J].海洋工程，2019，37（3）：86?94.

[14] 王恩重，陶传奇.基于改进蚁群优化算法的云计算调度方法[J].计算机与数字工程，2019，47（4）：743?747.

[15] 王嘉怡，房俊，高鹏.面向电能质量数据采集的蚁群优化算法[J].计算机与数字工程，2019，47（3）：524?529.