基于随机场理论的隧道开挖对附近建筑物的不均匀沉降及地表变形的影响分析

刘伯成， 包 昊， 姚方正， 慈 伟

（1.无锡地铁集团有限公司，江苏无锡 214000； 2.河海大学土木与交通学院，南京 210024；3.西南交通大学交通隧道教育部重点实验室，成都 610031）

随着我国经济的迅速发展，城市化进程的不断加快，地面道路已经不能满足现有的交通水平，地下隧道工程已经在我国各个城市广泛建设，因此会不可避免地穿过城市建筑物的下方，由此引发的一系列建筑物不均匀沉降成为相关工作者最为重视的问题. 近几十年以来，国内外许多学者对新建隧道施工对地表的沉降和位移的分析已经相当全面和成熟［1-5］，但是新建隧道施工对邻近建筑物附近土体的变形以及建筑物本身的不均匀沉降的分析相对较少. 朱育才等［6］对隧道扩建对周围建筑的影响进行了分析，研究了隧道开挖的影响半径；贺恒炜［7］研究了双线隧道开挖对于上部结构变形规律的影响，结果表明建筑物变形与相应的地面变形相一致；朱江涛［8］开展了隧道的开挖对接近施工建筑物的影响，研究表明双线隧道开挖的不同次序对于施工建筑的沉降有较大影响；葛卫娜［9］提出了治理隧道开挖造成建筑物损害的治理措施. 以上学者在该方向上都做出了极大的贡献，取得了丰硕的成果，然而多数学者仍然停留在均质土体的假设之下进行建模分析，忽略土体的成层性以及空间变异性，不同位置不同深度土体的物理力学参数必然存在差异，只将土体作为均质材料分析显然偏离实际情形，使其在一定程度上低估工程问题的危险性. 因此，需进行随机性的模拟分析，在土体弹性模量空间变异的基础上，研究隧道开挖对所测结果的影响.

1 非嵌入式随机有限差分分析

1.1 土体参数随机场理论

“空间变异性”的概念最初由P.Lumb［10］提出，指明由于土体的沉积作用使得物质组成存在差异，在经过若干时间的外力作用之后使土的物理力学参数呈现变异的特性. 常见的随机场的生成方式有很多，如：中心点法、协方差矩阵分解法、谱表现法等等，本文用谱表现法［11］建立随机场.

国内有诸多学者对土体的平稳随机场进行了研究分析. 程红战等［12］探索了土体弹性模量的空间变异性对地表水平和竖直向位移的影响规律. 不同的变异系数以及相关距离对地表竖向以及水平向的位移曲线在形态和量值上有不同的影响，变异系数的改变只影响位移曲线的量值而不改变形态，而相关距离的改变既改变形态又改变量值. 最后引入沉降监测值对地表变形进行概率分析. 方超［13］以围岩密度、弹性模量和内摩擦角这3个参数建立三维随机场，研究了围岩的竖向与水平向相关距离的变化对隧道结构变形的影响，并且说明在条件有限的情况下，应将更多精力投入于竖向相关距离的勘察. Huang等［14］建立了土体弹性模量空间变异性的随机场模型，对隧道衬砌的收敛进行可靠度分析，探讨了在各向同性和各向异性随机场中相关距离的改变对隧道衬砌收敛的均值和变异系数的影响，并将各向同性和各向异性以及各向异性中水平和竖向相关距的衬砌收敛的结果进行比较.

1.2 定义和模拟弹性模量随机场

随机场的特征是一个分布（如对数正态类型）和一个空间相关结构. 本研究认为土体的弹性模量为对数正态分布，这与某些土壤性质的现有现场数据一致［14］. 通过正态（高斯）分布的非线性变换可以很容易地得到对数正态分布，它保证了随机变量总是正的. 这样的分布也被一些研究者用于建立不排水剪切强度的模型［15］以及地基［16］和边坡［17］有关的概率研究.

本研究采用二维自相关函数定义随机场的空间变异性：

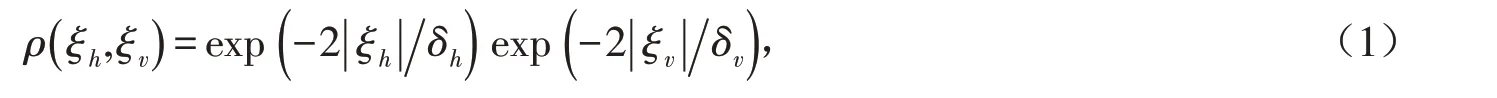
其中：ξh和ξv分别为水平方向和垂直方向任意两个位置之间的滞积距离；δh和δv分别定义了水平方向和垂直方向衰减率的波动范围（SOF）. 空间相关长度越大，说明土壤性质的相关距离越大，空间变异性越小，均匀性越好. 反之，相关长度越小，土壤性质的空间变异性越高，均匀性越差.

1.3 非嵌入式随机有限差分模型

将随机场理论与有限差分法相结合，具体方法如步骤：①使用MATLAB 软件生成土体弹性模量的随机场，使用FLAC3D 软件建立土体和建筑模型；②将土体弹性模量随机场中的数值按照一定顺序映射到FLAC3D 模型的每一个单元中进行计算，得出数据、整理数据；③进行N次步骤②；④统计N次计算的结果，整理分析，将N次模拟所得数据与确定性数据相比较.

图1 表示一次平稳随机场的实现得到的弹性模量空间分布云图，图中蓝色的部分表示低强度的软弱土域，红色的部分表示高强度的刚硬土域，而绿色土域的强度则是介于两者之间.

图1 平稳随机场的一次实现Fig.1 A typical realization of stationary random field

2 隧道开挖对临边建筑的影响

2.1 有限差分模型

建立描述软土土体弹性模量空间变异性的二维数值模拟，使用FLAC3D软件计算出建筑物以及隧道上部土体附近的竖向位移，研究其作用规律. 数值模型隧道的直径D=8 m，隧道中心轴的埋深H=15 m，为浅埋隧道，模型长x=120 m，两边距隧道中心各60 m，高z=50 m，轴线方向取值1 m. 衬砌为混凝土材料，使用壳（shell）单元模拟，由于壳单元为整圆与实际衬砌结构不符，故需折减，一般折减系数取0.8. 土体为Mohr-Coulomb弹塑性模型，建筑物用长为20 m高为18 m的实体单元弹性模型，建筑为框架混凝土结构，故其密度较小，文中取值较为保守. 建筑物与土体之间用“移来移去”法［18］设定接触面，接触面参数按Messaoud等［19］研究结果取值：Kn=109Pa/m，Ks=109Pa/m，黏聚力和摩擦角均按照土体的参数取值. 模型的有限差分单元网格如图2所示，模型中土体、建筑物和衬砌参数如表1所示.

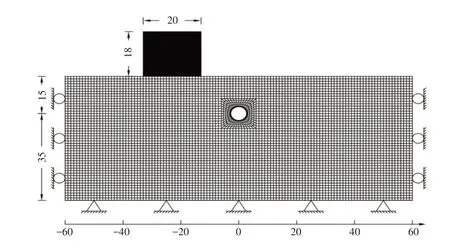
图2 模型几何形状（单位：m）Fig.2 Model geometry

2.2 确定性分析

由于隧道不是一次性开挖完成的，故需使用应力释放来模拟隧道开挖过程［20-21］. 其原理是开挖掌子面上由于土体的转移而失去原有的支撑，用FLAC3D计算一步（step 1）获得其不平衡力，将该面上的不平衡力乘以（1-γ）反向施加于原来隧道的表面上，其中γ为应力释放系数取值0.25.

在不考虑土性空间变异的前提下，即土体的弹性模量都按表1中取值20 MPa，经计算可得：建筑物左角点、右角点以及隧道正上方的位移分别为6.39、17.05、25.56 mm. 这些确定性的计算结果将在以下章节与随机性的计算结果相比较.

表1 物理力学参数Tab.1 Physical mechanical parameters

2.3 随机性分析

结合蒙特卡洛模拟（MCS）方法和随机场理论，研究土体在土性参数空间变异的条件下，隧道开挖对旁侧建筑物的影响. 假设弹性模量的均值为20 MPa，开展400次（N=400）MCS计算分析. 图3表示MCS次数与关键点沉降概率特征值的关系，可以看出，随着模拟次数的增加，4个关键点的沉降均值和标准差都趋于稳定，从计算精度和效率等角度考虑，N=400 符合计算要求.

图3 关键点的收敛趋势Fig.3 The converging trend of the key point statistics

将400次随机性的计算结果与确定性情形进行对比分析（图4）. 由确定性的计算结果曲线可得建筑物与土体的接触面的沉降呈线性，这是由于建筑物的弹性模量远远大于土体的弹性模量，故可将建筑物看作刚体. 隧道正上方地表附近的沉降规律基本服从以隧道中心为对称轴的高斯分布. 由随机性的计算结果可得400次MCS计算沉降曲线的大致趋势相同，但具体数值不同，与确定性结果相比，随机性分析的沉降曲线在一定范围内波动. 其中建筑物左角点、右角点、隧道正上方沉降最大值以及均值和标准差如表2所示，建筑物的不均匀沉降均值为12.96 mm，大于确定性不均匀沉降值10.69 mm.

图4 随机性与确定性结果对比曲线Fig.4 Comparison curves of randomness results and certain results

表2 随机性沉降值Tab.2 Random settlement values

图5为400组随机数据的沉降均值曲线与确定性曲线的对比，可以看出均值曲线更加平滑，均值曲线总体在确定性沉降曲线的上方，这表明确定性情况在400组随机模拟中处于较大值. 由标准差可看出建筑物左右角点的沉降变化幅度大于隧道正上方土体的沉降幅度. 而整个随机模拟的包络线基本都处于均值加减3倍标准差（δ）的范围内，这也明确了随机性的浮动范围.

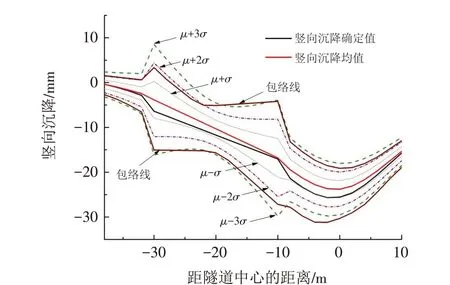
图5 随机性均值与确定性结果对比曲线Fig.5 Comparison curves of random mean values and certain results

即便400组模拟的弹性模量均值都是20 MPa，但是各模拟中所对应土体的“有效弹性模量”不同.“有效弹性模量”指某一空间范围内土体总的等效模量［22］，相当于对应均质土体中发生相同地表位移时的土体弹性模量. 如图6所示，左图为发生沉降最大值时的随机场，整个土体由大面积的蓝色区域覆盖即软弱区域占据主导，而右图则由大面积的红绿色刚硬区域占据，这就导致了左边模拟时的土体有效弹性模量远小于右边，从而形成沉降的两个极端情形. 同理，400 组模拟的均值相同但其各次的“有效弹性模量”不同，故每一次模拟的结果形成较大差别，这就造成了图4中的灰色的范围浮动.

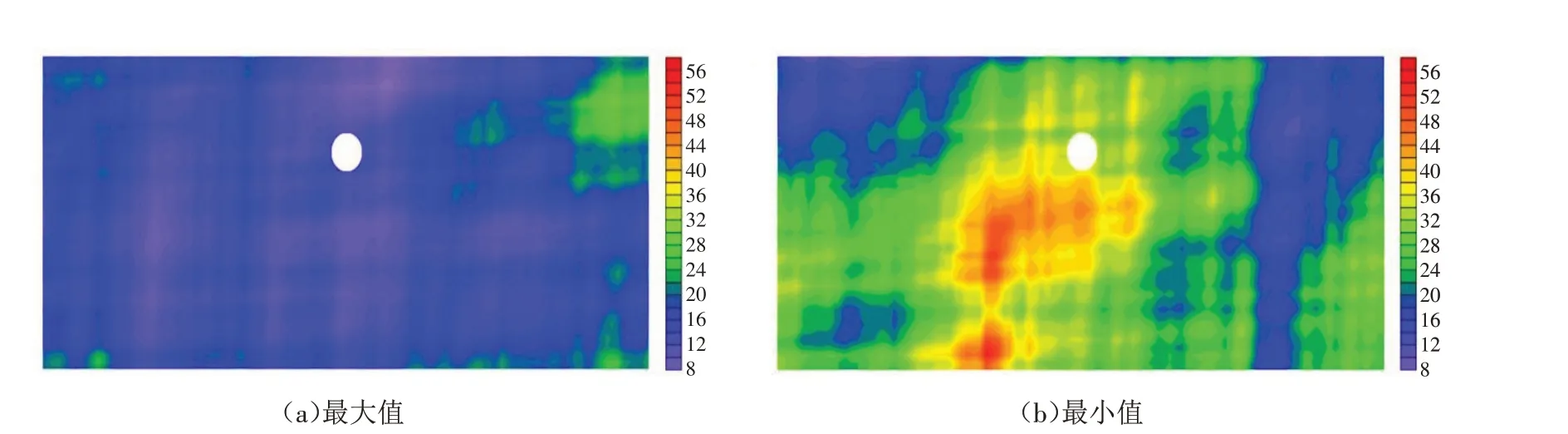
图6 沉降最大值和最小值的随机场对比Fig.6 Comparison of the random fields of maximum and minimum settlement values

图7为隧道正上方点沉降值的概率密度，沉降值大都集中在-24 mm左右即位于沉降均值附近，整个图形从均值附近依次向两边递减. 从概率分布类型上来看，沉降点的概率分布与对数正态分布近似，同时这也与形成弹性模量的分布函数相同.

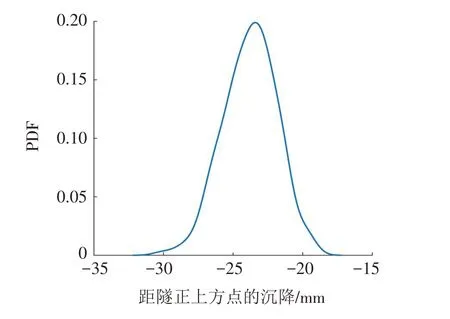
图7 隧道正上方点的沉降概率密度Fig.7 The settlement probability densities at the points directly above the tunnel

根据以上的模拟情况以及均值和方差数值表明：在实际情形中，隧道的开挖也会使得建筑物和地表的沉降高于预估值，在防护技术与措施有限的情况下更高的沉降最大值可能会使得临边的建筑物处于沉降过大的风险之中，故如需制定合理的防护措施以及支护方案，需要在设计时考虑土体物理力学参数的空间变异性.

3 结语

1）使用随机场理论与FLAC3D软件相结合的办法，在模拟隧道开挖时对建筑物的影响的问题中合理考虑加入土壤相关参数的空间变异性质问题.

2）在隧道开挖时，土性参数的空间变异性对临边建筑的沉降有直接的影响，传统的分析中将土体作为均匀物质忽略了这一要点，这将会在某种程度上高估隧道开挖时，周围建筑的安全性. 需考虑当地土体的实际情况，制定合理的方案.

3）从MCS计算分析结果可看出，在土性参数空间变异的前提下，建筑物角点以及地表沉降的数值变得极为不稳定，在一个范围内浮动，这是由于各模拟中所对应土体的“有效弹性模量”不同从而产生不同的位移值，同时也说明了实际工程中若不考虑土体空间变异的条件会低估沉降最大值，高估建筑物结构的安全性.