基于变密度地下水流模型分析预测沿海地区海水入侵

张 野

(辽宁省盘锦水文局，辽宁 盘锦 124010)

1 研究区概况

大清河发源于营口市东部山区，流域面积1468km2。该区内主要的地表水体为大清河地表水系，河床宽度约20～300m。为监测大清河的水位、流量、流速等信息，1959年，在大清河的中下游修建了望宝山水文监测站。根据望宝山水文监测站多年观测，大清河最大径流量为57m3/s，最小径流量为0.316m3/s，其径流随季节变化明显。为调节大清河径流量随季节的变化，在其上游修建了石门水库。此外，在大清河下游修建了一座集蓄水、灌溉、挡潮等功能于一体的拦河闸。

该区潜水含水层的主要补给来源主要有大气降水入渗、河流侧向补给、山前地下水径流补给、下伏碳酸盐岩岩溶水的顶托补给、山前冲洪积扇的侧向径流补给和开采条件下的越流补给。含水层接受河流侧向补给、大气降水入渗补给等多项补给后，沿地势自东向西流，径流速度随着含水层厚度、透水性和地形的变化而变化，在滨海地带含水介质的颗粒逐渐变小，透水性相应减小，地下水径流也随之减缓。天然状态下，大清河流域在上游河段地下水向河流排泄，在下游河段枯水期受地下水补给，丰水期河水补给地下水。随着工农业发展，用水需求增加，大清河流域先后修建了4个水源地(井深较深，分布在第四层中)，自上游至下游依次是团甸水源地(19口井，其中研究区涵盖4口)、化纤水源地(8口井)、盖州二三水源地(13口井)、永安水源地(18口井)以及大量农业机电井(井深较浅，分布在第二层)来满足供水需求。自水源地开采井和农业用井修建以来，人工开采已经成为地下水最主要的导出方式。由于农业灌溉用井和水源地开采井对地下水大量开采，地下水位低于河水水位，研究区地下水不再向河流排出，而是长时间受河流补给，由于河流补给速度和补给量有限，在水源地开采井和农业灌溉井广泛分布的永安水源地附近形成降落漏斗。

2 水文地质

大清河流域面积较广，在其上游地区河岸阶地狭窄，面积较小，望宝山下游河谷平原逐渐开阔且望宝山水文监测站水位监测资料齐全，作为已知水头边界能够反映出上游河流对下游地区的影响。因此，研究区模拟范围为：南北两侧以低山丘陵为界，东侧以望宝山水文监测站为界，西侧延伸至辽东湾距海岸2km处。模型的各边界设定如下：南北两侧含水层受山前地下水径流补给、山前冲洪积扇的侧向径流补给等多项侧向补给，是已知流量边界；东侧根据望宝山水文监测站多年水位监测数据可定义为已知水头边界；西侧边界取海岸向海洋延伸2km处，可定义为已知潮汐水头H(t)(淤泥质海岸，水头值恒大于等于淤泥质海岸顶板高程)边界和已知Cl-浓度20g/L边界(该区监测资料以Cl-浓度为主)；拦河闸可作为已知水头边界；区域内河段在模型中作为河流处理(已知水头和河床底板高程)；底部隔水岩层可视为零流量边界；含水层与大气之间的水分交换发生在潜水含水层，包括大气降水(大气降水量取营口气象站测定的1991—2015年年平均变化降水量进行赋值)和蒸发(蒸发极限深度为4m，研究区地下水位埋深多大于4m，因此蒸发量忽略不计)；源汇项主要有农业开采井(在农耕区按照1.5口井/km2进行布设，共有90口井)和水源地开采井(下游3个水源地的所有开采井和团甸水源地的4口开采井)。

3 数值模型

数学模型，变密度水流方程为

(1)

式中：hf为等效淡水水头,m;Kf为等效淡水渗透系数,m/h;ρf为淡水的密度,kg/m3;ρ为实际液体密度,kg/m3；Z为位置点高程,m;Sf为等效淡水弹性释(储)水率,1/m;t为时间,h;θ为有效孔隙度;C为溶质浓度,mg/h;ρs为单位体积源(汇)项的密度,kg/m3;qs为单位体积源(汇)项的流量,m3/s。

式(1)加上相应的初始条件和边界条件，就构成了描述地下水流运动的数学模型[1]。定解条件可表示为

初始条件：

H(x,y,z,0)=H0(x,y,z)

(2)

第一类边界条件：

H(x,y,z,t)|Γ=H1(x,y,z,t)

(3)

第二类边界条件：

(4)

式中：H0(x,y,z)为研究区各层初始水头值；H1(x,y,z,t)为研究区各层第一类边界上的实测水头值；q(x,y,z,t)为研究区各层第二类边界上的单位面积流量[2]。另外，由于不考虑溶质运移过程中的化学反应，因此溶质运移方程表达式为

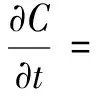
(5)

式中：C为溶质浓度,mg/L;D为溶质扩散系数,m2/h;Cs为单位体积源(汇)项的溶质浓度,mg/L。

式(5)加上相应的初始条件，就构成了地下水溶质运移的数学模型。定解条件可表示为

初始条件：

C(x,y,z,0)=C0(x,y,z)

(6)

第一类边界条件：

C(x,y,z,t)|Γ1=C1(x,y,z,t)

(7)

式中：C0(x,y,z)为已知的浓度分布；C1(x,y,z,t)为研究区各层已知浓度边界上的实测浓度值。

3.1 模型离散

在水平方向上, 将该模型离散为100m×100m的矩形网格, 垂向上依照相应的含水层特征进行划分。模型共分成5层, 激活边界内单元格，有效单元格共有9个。模型模拟的校正期是1991年11月至2015年11月，将两年作为一个模拟区间，两个月作为输出时间步长。

3.2 模型识别

初始含水层水平渗透系数根据辽宁地质勘察报告抽水试验所得结果进行赋值，假设水平渗透系数是垂直渗透系数的10倍。该区内共有3个水位监测井和3个多年浓度(含盐量)取样点，将计算出的水位和浓度与监测的水位和浓度进行匹配，通过调整渗透系数、弹性释(储)水率进行标定(即模型识别的主要参数是渗透系数和弹性释水率)，以满足水流场和浓度场以及水头和Cl-溶度随时间的分布规律[3]。反复标定至3个水位观测井(W1、W2、W3)的水位观测值和计算值之间的平均绝对误差小于观测值的10%，3个浓度观测井(W4、W5、W6)的浓度观测值和计算值之间的平均绝对误差小于观测值的10%。使得最后的水流场和浓度场分别与真实水流场浓度场相似，识别参数结果见表1，另外，水平渗透系数是垂直渗透系数的5倍。模型中剩余的参数没有进行识别，根据已有模拟案例取经验值，其中孔隙度为0.3，纵向弥散度和横向弥散度分别为500m和50m，扩散系数设定为1×10-4m2/d。

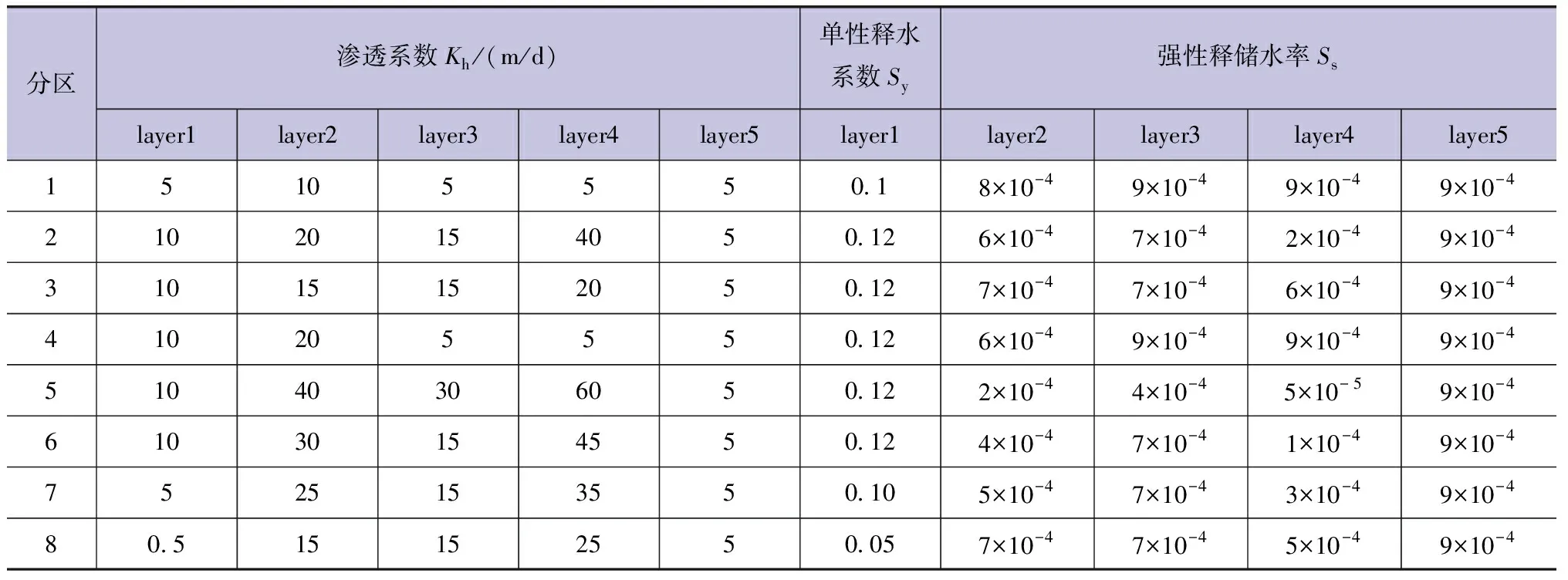
表1 研究区分区水文地质参数识别结果

该区内观测井观测数据与计算值之间的拟合曲线见图1，2015年计算水位见图2。从图2中可以看出，无论是水位观测井还是浓度观测井的水位观测值还是浓度观测值，与模拟计算所得变化趋势都是基本相同的。从图1中可以看出，水位与浓度的计算值均在观测值之间均匀地波动，造成这种现象的原因可能是模型上边界大气降水赋值是按照年平均降水量进行的，在一个模拟区间内，计算水位是该时间区间内水位变化的平均值，监测水位是具体时间点的水位。

3.3 模型验证

为了验证降水量的时间不均一性是否是产生上述误差的原因，选取2015年11月至2016年11月作为模型的验证期。在模型验证期内降水量按照实际月降水量进行赋值，其他参数不变，将1个月作为一个模拟区间，3天作为一个输出时间步长进行运算。将水位监测井(W1、W2、W3)的计算水位值分别与实际水位进行对比，见图3，通过验证可知，该模型可以对海水入侵未来趋势作出分析。

4 模型不确定性分析与模拟结果

4.1 模型参数不确定性分析

建模中含水层的划分是按照实际含水层结构和分布确定的。由于河谷平原实际含水层面积自上而下是逐层减少的，为使计算结果稳定、收敛，假设模型的每一层含水层面积相等，而每一层含水层多出的面积部分赋予较小的渗透参数值[4]。通过多组计算对比，对计算结果产生的误差很小，可以忽略。

该区降水入渗系数是按照已有研究的经验数据进行赋值的。由于模型校正周期时间较长，在校正过程中直接取年均降水量值进行计算[5]，而在验证模型过程中按照月均降水量进行赋值。对比同一时间按年均降水量与按月均降水量赋值的计算结果，误差较小，可忽略。因此，在后期对未来20年的预测分析中可按照多年降水量的平均值进行赋值。

由于该区海岸带地势平坦，滩涂可向海岸带延伸约2km，因此，在建立模型边界范围时向海岸带延伸了2km，并将滩涂范围设定为潮汐水头。对海岸带延伸距离进行敏感性分析，分别假定海岸带延伸距离为1km和3km。模拟结果表明，潮汐作用条件下，海岸带延伸距离对结果的影响较小，边界延伸距离的变化对模拟结果影响并不十分敏感。

4.2 模拟结果

该区1991—2015年的模拟结果显示，地下水的过度开采(研究区降雨补给平均约1700万m3/a，侧向补给400万m3/a，河流流量约2500万m3/a，水源地和农业井的最大开采量约5500万m3/a，补给量小于开采量)在大清河的南侧永安水源地附近形成了一个降落漏斗，见图2，降落漏斗中心水位最低时约-16m，浓度等值线(见图4)则由于密度差异、分层水文地质参数不同、分层开采量不同等原因呈现出图4(a)～图4(e)中的分层差异，分别代表研究区第1～5层的浓度分布。从图4(a)中可以看出，第1层海水入侵主要受潮汐波动的影响，拦河闸下游的大清河河道在潮汐作用下，高潮位海水沿河道上溯，出现高浓度入侵锋；从图4(b)中可以看出，第2层由于大量农业灌溉开采地下水，第1层地下水下渗补给时，携带Cl-向降落漏斗中心入侵，由于北岸河谷平原面积较小，农业井较少，大清河北岸海水入侵程度明显低于南侧。图4(c)和图4(d)则表明第3、第4层含水层海水入侵基本不受潮汐作用的影响，主要是由于第4层内水源地开采井大量开采地下水，海水沿指向内陆的水力坡降向内陆运移。从图4(d)和图4(e)中可以看出，第5层与第4层浓度分布几乎无差异，其原因可能是第5层渗透系数相对较小，该层入侵主要由第4层已入侵部分在重力作用下渗透。因此，该区发生海水入侵的主要原因有两方面，一方面是潮汐作用下的海水沿河道上溯，并向四周补给低水位地下水所产生的入侵；另一方面是由于地下水的大量开采形成降落漏斗，降落漏斗中心水位远低于海平面，产生指向内陆的水力坡降，海水沿水力坡降方向入侵[5]。

设定浓度小于250mg/L的地区是未入侵区，天然无开采条件下研究区入侵面积定义为A0，某一时间节点对应的入侵面积定义为At，则某一时间节点对应的海水入侵面积为ΔAt=At-A0[6-9]。研究区2012年开始实施压采方案对各水源地开采量进行控制，2012—2013年初步压采(永安水源地和团甸水源地开采量减半)，2014—2015年再次压采(各个水源地的单井开采量均不超过1000m3/d), 但由于对农业灌溉井并未进行约束，加之降落漏斗中心水位未恢复至海平面以上，研究区整体水力梯度仍由海洋指向内陆[10]。计算所得研究区实施水源地压采之后逐年分层入侵面积变化情况见表2，可以看出，压采方案实施后，250mg/L的入侵等值线仍旧向内陆侵移，入侵面积加大。除地表受潮汐作用影响较大外，下部地层入侵速率虽有波动，但整体上呈减缓趋势。

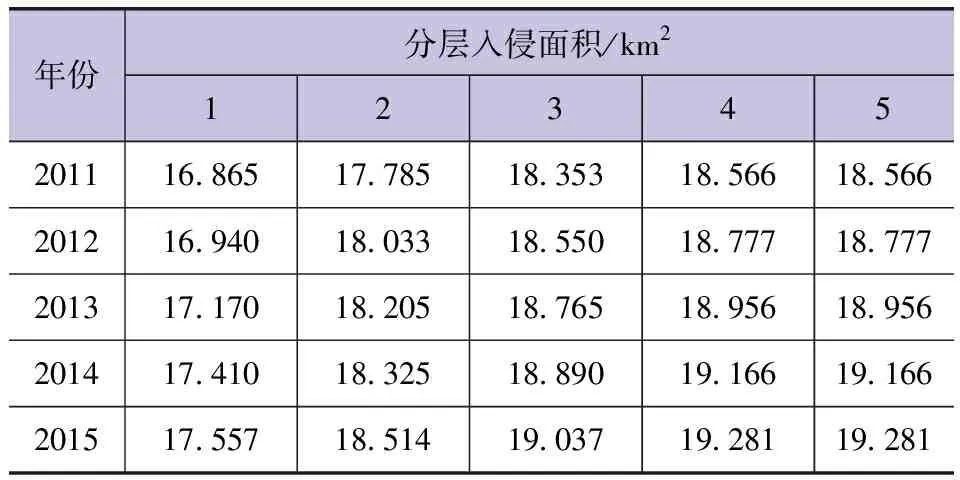
表2 压采后逐年分层入侵面积变化情况

5 结 论

从以上分析可以看出监测数据与计算数据变化趋势一致，且计算值与观测值之间的绝对误差小于5%。从监测井数据与计算数据的水位对比曲线来看，模型识别所得参数基本符合研究区实际情况，可以用来预测研究区未来海水入侵的趋势。由此可知，采用变密度地下水流动数学模型研究区域海水入侵过程，将会是未来发展的方向。