考虑需求拆分的多时间窗集送货车辆调度优化研究

蒋禄欢

考虑需求拆分的多时间窗集送货车辆调度优化研究

蒋禄欢

（重庆交通大学 经济与管理学院，重庆 400074）

车辆调度是连锁超市物流配送的重要环节，目前只考虑时间或距离的单一约束条件下的车辆调度已经不能满足市场需求，因此以JLF连锁超市为研究对象，考虑了需求拆分、多时间窗和集送货三者同时约束下的车辆调度模型，运用动态规划顺序法进行求解，研究表明考虑需求拆分的车辆调度问题更具现实意义。

车辆调度；需求拆分；多时间窗；动态规划

1 引言

随着现代经济的高速发展，人民生活水平提高，连锁超市在零售业行业得到了广泛的关注。连锁超市进行货物配送时，大多数门店存在集货和送货需求，在各个门店规定的时间内，将货物从配送中心配送到各个分店，这一过程涉及到运输成本、惩罚成本和货损成本等，研究如何进行配送车辆的分配和配送路线的规划，可以达到降低成本、提高规模效益的目的，这样就产生了连锁超市车辆调度优化问题。

传统的车辆调度问题由DANTZING和RAMSER[1]在1959年首次提出。目前，中国对于一般的车辆调度问题研究已经较深入。张江华等[2]建立了集送货车辆调度问题的多目标规划模型。针对需求可拆分车辆调度问题，刘旺盛等[3]设计了求解该问题的聚类算法，熊浩等[4]构建了一种基于双层规划模型的三阶段禁忌搜索算法。王科峰等[5]提出了带时间窗约束的需求可拆分的集送货车辆调度问题，构建了该问题的数学模型。在上述研究中，大多数是单一约束条件下的车辆调度问题，并且对于具体的连锁超市车辆调度问题，大部分文献也只局限于考虑时间或距离最优化，没有充分考虑连锁超市复杂的配送要求。

和上述文献不同，本文从连锁超市统一配送特点出发，将研究对象确定为考虑需求拆分的多时间窗集送货车辆调度优化研究。

2 需求拆分的多时间窗集送货车辆调度模型

考虑需求可拆分的多时间窗集送货车辆调度问题可以描述为：连锁超市拥有一个配送中心，配送中心有一定数量已知载重量的运输车辆，现在有个门店有货物需求，其中每个门店的要求都包括集货和送货两方面，车辆从配送中心出发，到达门店满足其集送货需求，每个门店的集送货量允许拆分成为不同车辆完成，车辆满足所有门店的需求后回到配送中心，同时每个门店对货物有时间窗要求，超过要求时间会产生一定的惩罚成本，基于上述要求，求满足配送需求的成本最少的车辆行驶路径。

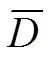
min=1+2+3+4（1）

j≤（4）

j≥i+j－j－（1－ijk） （5）

j≤i+j－j－（1－ijk） （6）

j=i+ij+i（7）

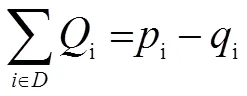
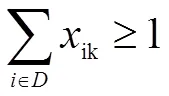
ik∈{0，1}，ijk∈{0，1} （10）

jk≥0 （11）

其中，公式（1）表示以成本最低为目标函数，公式（2）表示门店服务的车辆数等于离开点的车辆数，公式（3）表示车辆装载量不超过总装载量，公式（4）表示车辆装载量不超过容量限制，公式（5）（6）表示车辆装载量等于前装载量减需求量加供应量，公式（7）表示时间窗约束，公式（8）表示门店的所有集送货需求，公式（9）表示门店有一辆或以上车经过，公式（10）（11）表示变量和取值的约束。

3 案例分析

已知JLF配送中心的配送时间是05：00—08：00，配送中心有5辆容量为3 t的车辆，配送车辆05：00从配送中心出发，货物运输单价2元/km，车辆固定成本100元/辆，车辆行驶速度40 km/h，货物平均单价3 000元/t，平均卸货速度0.2 h/t，货损系数0.2%，惩罚系数0.05%。门店距离、门店基本信息分别如表1和表2所示。

表1 门店距离表（单位：km）

PABCDEFGHI P0 A21.10 B2912.60 C30.912.220 D34.516.64.34.50 E35.417.65.73.53.40 F40.118.86.36.72.35.10 G38.818.8211921.718.523.60 H45.528.616.116.41215.59.930.10 I34.92920.822.720.724.219.641.721.80

表2 门店基本信息

送货量（收货）集货量（退货）要求时间窗可接受时间窗 P A1.50.505：1006：2005：0006：40 B1.0 05：2006：0005：0006：10 C1.20.205：4006：3005：3006：40 D0.7 06：0007：1005：5007：20 E1.2 05：5007：3005：4007：50 F1.3 06：1007：4006：0007：50 G1.1 05：3006：4005：2006：50 H0.90.206：1007：3006：0007：40 I1.0 05：2006：3005：1006：40

从门店P出发，分别计算各路线运输成本、货损成本和惩罚成本选择总成本1（2）最小的路线为第一阶段最优决策1（1）。第一次动态规划第一阶段如表3所示。

第一阶段选出门店P到门店A点成本最小，进入第二阶段规划，从门店A出发，比较门店A到各门店的总成本，选出成本最小路线即为第二阶段最优路线。第二阶段如表4所示。

在第三阶段计算中，门店E集送货需求量被拆分，其送货量1.2 t被拆分为1 t在此次运输中完成，剩余0.2 t转移到虚拟门店E1，虚拟门店E1与门店E地位相等，虚拟门店E1进入第二次动态规划。第一次动态规划第三阶段如表5所示。

表3 第一阶段

s2D1（s2）s1v1（s2，u1）v1（s2，u1）+f0（s1）f1（s2）最优决策u1（s1）车辆载重/t AP—AP51.2151.2151.2P—A1.0 BP—B64.0164.0164.0 CP—C69.0169.0169.0 DP—D81.9181.9181.9 EP—E78.0178.0178.0 FP—F107.2207.2207.2 GP—G84.2184.2184.2 HP—H98.8198.8198.8 IP—I75.8175.8175.8

表4 第二阶段

s3D2（s3）s2v2（s3，u2）v2（s3，u2）+f1（s2）f2（s3）最优决策u2（s2）车辆载重/t BA—BA∞∞∞A—C CA—C31.6182.8182.82.0 DA—D37.4188.6188.6 EA—E42.4193.6193.6 FA—F45.4196.6196.6 GA—G44.2195.4195.4 HA—H 62.6213.8213.8 IA—I77.7228.9228.9

表5 第三阶段

s4D3（s4）s3v2（s3，u2）v2（s3，u2）+f1（s2）f2（s3）最优决策u2（s2）车辆载重/t BC—BC∞∞∞C—E3.0 DC—D13.2196.0196.0 EC—E13.0195.8195.8 FC—F19.4202.2202.2 GC—G∞∞∞ HC—H38.2221.0221.0 IC—I∞∞∞

在考虑需求拆分的情况下，第一次动态规划路线：P—A—C—E，总成本195.8元，运输时间108 min，运输距离36.8 km。剩余门店BDE1FGHI进行第二次动态规划，经过4次动态规划，完成所有门店的配送任务，得出考虑需求拆分下的4条配送路线如表6所示。

表6 数据对比

运输路线成本/元时间/min距离/km车辆数/辆 需求不拆分P—G184.271.438.81 P—I—F222.8109.454.51 P—B—E—H244.6114.950.21 P—A—C—D196.0105.937.81 合计847.6114.9181.34 需求拆分P—I—F1—H—G308.2113.284.61 P—A—C—E195.810836.81 P—B—E1—D—F198.896.640.41 合计702.8113.21253 差值144.81.756.31

可以看出在考虑需求拆分的情况下，门店E和门店F的需求量被拆分为两次完成，减少了车辆调度安排，一定程度上简化了HY连锁超市配送的复杂性。因此考虑需求拆分比不考虑需求拆分下的总成本降低了144.8元，运输时间减少了1.7 min，运输距离减少了56.3 km，考虑需求拆分下的车辆调度安排更合理。

4 结论

本文以JLF连锁超市为例，运用动态规划顺序法，在考虑需求拆分的条件下，对门店E和门店F需求量进行拆分，让配送车辆两次访问门店E和门店F，重新安排其配送路线，并且对比需求不可拆分的情况，考虑需求拆分下的HY连锁超市集送货车辆调度安排，可以有效减少JLF连锁超市的配送成本和配送资源的浪费，提高企业效益，因此对于考虑需求拆分的连锁超市集送货车辆调度问题的研究具有一定的实际意义。

［1］DANTZING G B，RAMSER J H.The truck dispatching problem［J］.Management Science，1959，6（1）：80-91.

［2］张江华，李进，高敏刚.同时集散货物的开放式车辆调度问题研究［J］.中国管理科学，2013，21（4）：187-192.

［3］刘旺盛，杨帆，李茂青，等.需求可拆分车辆调度问题的聚类求解算法［J］.控制与决策，2012，27（4）：535-541.

［4］熊浩，鄢慧丽.需求可拆分车辆调度问题的三阶段禁忌算法［J］.系统工程理论与实践，2015，35（5）：1230-1235.

［5］王科峰，叶春明，唐国春.带时间窗分车运输同时收发车辆调度问题及其启发式算法［J］.运筹与管理，2012，21（2）：83-88.

U492.3

A

10.15913/j.cnki.kjycx.2020.18.007

2095－6835（2020）18－0018－03

蒋禄欢（1996—），女，研究生，研究方向为物流管理。

〔编辑：王霞〕