新零售目标产品的精准需求分析与预测

吴琳洁，郑钰洁，范云飞

新零售目标产品的精准需求分析与预测

吴琳洁1，郑钰洁2，范云飞2

（1.暨南大学数学系，广东 广州 510632；2.暨南大学伯明翰大学联合学院，广东 广州 510632）

在中国商品社会逐步发展，消费需求不断升级的今天，产品多样化、个性化需求使得相应销售数据层级复杂，品类繁多，因此建立一个对区域层级、小类层级消费分析和需求预测模型具有重大意义。针对新零售行业精准化需求进行建模，主要分析了销售特征、库存信息、节假日折扣等因素对销量的影响，通过建立主成分多元模型对未来销售数据进行预测，同时利用平均绝对百分比误差法获得预测数值的精准度。通过绘制散点图以及对平均绝对百分比误差（MAPE公式）的分析，得到模型预测值的MAPE值在15%～35%之间，可以认为模型灵敏度较高。因此，零售行业可选择主成分多元模型对未来销量进行预测，从而减少缺货、库存成本，有利于提高经济收益。

需求分析；需求预测；主成分分析；多元线性回归

1 引言

随着中国消费市场新业态继续涌现并快速发展，主流消费模式由“以物为主”逐步向“以客为主”转变。对于零售行业，促进消费者需求的主要因素不再单是性价比等客观商品特质，以时尚性为表现形式的个性化、审美化、多样化的主观因素同样渐成消费主导需求动力。

新零售时代，零售企业将采取多品种小批量的生产形式，以适应新时代消费需求。这将导致商品小类井喷式增加，商品个性化特色强烈，零售行业商品分类管理困难，面临消费数据层级复杂、种类繁多等一系列新的挑战。

如何为更精细化分级至SKC（单款单色）层级的商品提供精准的数据分析和销售预测至关重要。本文基于主观性与客观性两个方面来分析影响因素，并在此基础上建立基于主成分分析的预测模型，但单一的预测模型可能会给结果带来较大的误差，因此建立多元线性回归模型形成复合预测模型，以提高模型的准确性。

2 数据处理

2.1 数据来源

数据来源为赛氪官网赛题（https://www.saikr.com/c/nd/ 6456）。根据相关问题对数据的需求和原数据的特点，首先使用R读取附件数据表，按照相应问题所需时间筛选出对应项目后对原始数据进行相关归类整合，接着对存在问题的数据进一步进行修正处理，过程如下。

2.2 相关数据

通过R整理，销售时间处于2018-07-01—2018-10-01内且累计销售额排名前50的skc，称为目标skc。再找出目标skc在对应节假日的销售额、销售量、标价、库存平均值和计算出的每种节假日期间的折扣。

通过R整理出排名前50的skc（目标skc）所属的小类在2019-07-01—10-01（即2019-10-01前后3个月）的销量数据及销量影响因素（折扣、库存、销售单价等）数据。

2.3 处理方法

分析整理后的数据发现，有部分skc没有标签价格。对于这部分没有标签价格的skc，本文将根据销售价格相似的其他skc的折扣幅度，运用插值的方法填充空白值。例如，双十一期间，对于编号为602573870209的skc，它在附件2中没有对应标价（tag price），因此使用与其销售价格相似的596573650847（折扣为0.86）与208573761122（折扣为0.81）等，再根据销量的相似程度对其进行加权插值，得出其折扣约为0.857。

缺失库存数据：对于没有库存数据的skc，首先定位其所在的小类，然后利用小类中其他skc的库存对其进行库存估算。

3 对销量的相关影响因素的分析

在研究如何对现代愈加精细化的小类需求做出预测之前，面临的实际问题是如何衡量各种影响因素对于销售量的影响程度。探讨销售量受销售特征、库存信息、节假日折扣等因素的影响。因此，结合基于附件1和附件4整合修正好的的数据，从主观和客观两个角度分析影响销售量的因素。

客观上，在2018年国庆节、双十一、双十二和元旦这四个节假日内，提取目标skc，分析库存信息、原价与标签价格等信息，再利用SPSS软件，得出相关性矩阵，以此分析客观上的相关性。

主观上，构建主成分分析法模型，根据该模型得到各种因素对目标skc销售量影响的贡献程度，以此分析主观上的相关性。

分析不同因素对目标skc销售量的影响，这些因素包括产品销售特征、库存信息、节假日折扣等信息，其中，将商品属于的小类（小类类别）与销售时间（在哪个节假日进行销售）作为产品销售特征；根据节假日商品的销售量（s）与当天实际花费（real cost）得出商品当天的销售价格（selling price），并与标签价格（tag price）作比，得出商品在节日当天的节假日折扣（discount）；利用附录三提取出目标skc的当天库存信息（inv）。

所统计的skc，=50个，相关因素共有4个，分别是折扣、库存、销售价格与小类，将数据放入矩阵。

由于各因素的数据相差过大，为了消除不同量纲的影响，避免对结果的准确性造成较大影响, 利用以下公式进行数据归一化：

基于归一化后的数据，从客观上的相关性与主观上的相关性分别进行相关性分析。

3.1 客观上的相关性分析

首先进行客观上的相关性分析，可以用皮尔逊（pearson）相关系数和斯皮尔曼（spearman）相关系数对变量间的相关程度进行测量，若被解释与解释变量之间相关性较高，则模型研究是有意义的；但是如果解释变量之间的相关性过高，可能会引起变量之间产生严重的多重共线性，从而影响模型结果。

jk为第，列数据的方差。

=-1-1（2）

式（2）中：为观测矩阵的Pearson相关矩阵；为样本观测的协方差矩阵。

利用SPSS分别得到所选节假日skc销量影响因素相关性矩阵，如表1所示。

表1 国庆相关性矩阵

折扣平均库存销售价格小类类别销售量 相关性折扣1.000-.399-.072-.183-.387 平均库存-.3991.000-.023.116.968 销售价格-.072-.0231.000.411-.170 小类类别-.183.116.4111.000.050 销售量-.387.968-.170.0501.000 显著性（单尾）折扣 .056.392.241.063 平均库存.056 .465.329.000 销售价格.392.465 .051.257 小类类别.241.329.051 .425 销售量.063.000.257.425

注：绝对值越接近1，表示相关性越大。

从表1可以看出，库存是客观上相关性最大的因素。其次是折扣，这是可以理解的，因为国庆的假期比较长，消费者可以有一段时间关注价格的动态，因此折扣也是影响消费者消费的主要客观因素。

双十一期间相关性矩阵如表2所示。

表2 双十一期间相关性矩阵

折扣库存销售价格小类类别销售量 相关性折扣1.000.252-.006.533.109 库存.2521.000-.065.346.536 销售价格-.006-.0651.000.024.128 小类类别.533.346.0241.000.190 销售量.109.536.128.1901.000 显著性（单尾）折扣 .149.491.009.328 库存.149 .395.073.009 销售价格.491.395 .462.301 小类类别.009.073.462 .218 销售量.328.009.301.218

根据表2结果，从客观上来看，库存与销量的相关性最大，这与实际生活是符合的。因为一般销售量较好的商品，商家会多准备一些库存，尤其是双十一时期，商家如果根据之前的销售记录可预感到销售会大幅增多，则会大大增加库存量，保证货源充足。其次是与小类和出售价格相关，最不相关因素的是折扣，这是因为顾客在挑选商品时一般很难了解到商品在一段时间前的价格，因此也无法得知折扣且通过折扣影响自己的消费行为的可能性很小。

双十二期间相关性矩阵如表3所示。

表3 双十二期间相关性矩阵

折扣库存销售价格小类类别销售量 相关性折扣1.000-.296.177-.033-.263 库存-.2961.000-.129.069.519 销售价格.177-.1291.000.442-.495 小类类别-.033.069.4421.000-.012 销售量-.263.519-.495-.0121.000 显著性（单尾）折扣 .109.234.447.139 库存.109 .299.389.011 销售价格.234.299 .029.016 小类类别.447.389.029 .481 销售量.139.011.016.481

从表3可以看出，库存依然是客观上相关性最大的因素，总体相关性与双十一类似，这与两个节日的相似性也有很大关系。

从2018年元旦（2017-12-30—2018-01-01与2018-12-30—2019-01-01）的统计结果发现，在目标skc中只有5个skc在元旦期间有销量，其中还有3个skc没有对应的标签价格与小类分类，而且这5个skc在这期间都没有库存信息，因此无法对其进行相关性分析。但是从中可以看出单价较低的skc销量略多于单价较高的skc。

元旦期间数据如表4所示。

表4 元旦期间数据表

skc日期销售量实际价格原价格折扣销售价格小类 3965738706602018-01-0181 3301 5900.836 478166.2527 217 089 6025738702092018-01-013380 126.666 7 6965722249502018-01-01101 051.25 105.125 9025733202752018-01-0111723.75 65.795 45 9965738705722018-01-0147007950.880 50317527 217 089

上面三个节日中，库存的相关性最大。但并不是说大肆增加库存，就会增加商品的销售量，因为库存并不能从主观上影响商品的销售量，因此称其为客观上的相关性。反而增加库存后卖不出去，会增加货物囤积成本，给商家带来不必要的损失。因此，有必要进行主观上的相关性分析，以此判定哪些因素能从主观上影响销售量的变化。

3.2 主观上的相关性分析

通过构建主成分分析法模型进行主观上的相关性分析，主要计算步骤如图1所示。

图1 主观分析计算步骤

首先计算样本标准差：

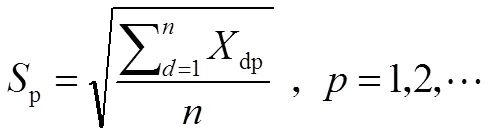
计算相关系数矩阵：

根据样本的相关系数矩阵, 计算出相关系数矩阵的特征方程，并计算出相应的特征值1≥2≥…≥m。根据方差特征值计算出方差贡献率，则有：

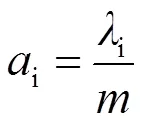
根据前面确立的影响因素以及已有的数据，利用SPSS软件对其进行分析计算，具体计算过程如下。以双十二为例，进行主成分分析，具体如表5、表6所示。

根据成分得分矩阵，得出双十二期间销量相关的因子的表达式如下：

1=0.325×－0.273×+0.552×－+ 0.423×－

2=－0.487×+0.532×+0.187×－+ 0.472×－

以每个因子的方差贡献率作为系数，对每个因子乘上系数后得到最终的双十一销售状况预测模型公式：

=0.150 7×1+0.128 7×2

成分得分系数矩阵和方差贡献率同样可以反映出不同因素对因变量的贡献程度，由此分析主观上的影响因素。可以看出在第一主成分中，销售价格与小类的贡献程度最高，即从主观上来说，商家如果在双十二期间压低自家商品的价格，很有可能会带来销售量的增加。也因此称其为主观上的相关性，即该因素的自身变化能带来销售量的变化。该公式是对双十二期间整体销售状况的一个呈现，可以用于后面的销量预测。

表5 双十二主成分分析表一

总方差解释 成分初始特征值提取载荷平方和 总计方差百分比累积/（%）总计方差百分比累积/（%） 11.50737.68437.6841.50737.68437.684 21.28732.18069.8641.28732.18069.864 3.70117.53587.399 4.50412.601100.000 提取方法：主成分分析法

表6 双十二主成分分析表二

成分得分系数矩阵 成分 12 折扣.325-.487 库存-.273.532 销售价格.552.187 小类类别.423.472 提取方法：主成分分析法，组件得分

同理，可以得到国庆期间的销售状况预测模型如下：

1=－0.452×+0.361×inv+0.347×－+ 0.445×－

2=0.383×－0.498×+0.527×－+ 0.358×－

以每个因子的方差贡献率作为系数，对每个因子乘上系数后得到最终的公式如下：

=0.159×1+0.124 8×2

双十一期间的销售状况预测模型如下：

1=0.452×+0.365×－0.2×－+ 0.477×－

2=0.09×－0.199×+0.962×－+ 0.107×－

以每个因子的方差贡献率作为系数，对每个因子乘上系数后得到最终的公式如下：

=0.176 8×1+0.101 6×2

4 销售量的预测

零售商品种类的繁多，使得零售行业的库存管理有很大的难度，而销量的不稳定，更会增加库存堆积、缺货等现象，加大企业的成本。而提前进行销售预测，可以最大限度避免库存积压、尾单、缺货等现象，减少企业的缺货成本和库存成本，从而提高企业利润。因此，根据目标小类的产品销售特征、库存信息、节假日折扣等因素，利用前面得到的模型，对10个目标小类进行预测。由于单一的预测模型可能会给结果带来较大的误差，因此建立多元线性回归模型，利用模糊分析法得出两种方法的权重，得到最终的预测值，并给出每个月预测值的。

前面模型是根据三个节假日（国庆、双十一、双十二）进行的分析，因此选择与之相吻合的时期（10-01后3个月）。可以直接对前面的公式进行整合，得到预测模型。统计目标小类在需要预测的时期的折扣、库存、销售均价（销售额/销售量），可以代入公式求解。对于原公式出现的小类项，因为要预测的项目即为小类项，所以将原公式的小类项舍弃，其他项不变，得到新的公式A´，B´，C´。因为双十一与双十二属于较重大的购物节日，与平时一般时间的销售状况可能存在差距，因此给其分配较低的权重系数，为40，国庆节较为接近平时一般状况，因此其系数为50。

可以得到加权修正后的基础预测模型公式：

4.1 多元线性回归模型

建立多元线性回归模型，对自变量1，2，…，p与因变量进行多元线性回归：

=（1，2，…，p）+（3）

式（3）中：为销售量；1，2，…，p为影响因素（销售额、销售均价、库存、折扣）；表示误差项。

利用公式=（T）-1T，得到回归公式=+。

以12月为例，利用Python进行计算，得到的值为[﹣2.580 3+03，8.465 2﹣03，5.795 2+00，8.456 2+03，﹣2.974 8+01]。

将值代入得到回归公式=﹣258 0.3+0.008 465 21+ 5.795 22+845 6.23﹣29.744。

需要预测的时期的销售额、销售均价、库存、折扣，这些影响因素代入公式即可得到预测值。

4.2 模型求解

通过将整合处理好的数据代入以上模型，可以得到12月份预测值的QQ图，如图2所示。12月份方差分析如表7所示。

图2 12月份QQ图

表7 12月份方差分析表

方差来源自由度平方和（SS）均方（MS）F值p值 回归（R）42.652 8e+0866 318 937.138 2103.729 95.368 7e-05 误差（E）53 196 711.547 1639 342.309 4 总和（T）92.684 7e+08

可以看到，点与直线有大致的拟合趋势，但仍存在较大误差，这是因为使用单一的预测模型会给结果带来较大的误差，单项预测方法会有自身的优点和限制条件。因此需要将前面的模型与多元线性回归模型进行整合，利用模糊分析法，得到最终的模型公式为=0.9×+0.1×。

12月份实际销售量与预测销售量对比如图3所示。

如图3可见，12月份预测销量和实际销量几乎重叠，说明直观上，最终的模型预测具有一定的可信度和准确性。公式如下：

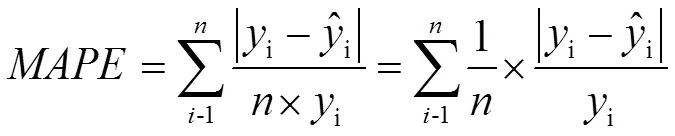
最后，对预测数据进行量化评估，运用公式计算得出，12月份预测结果的值为0.170 707，11月份的为0.355 463，10月份的值为0.289 616。

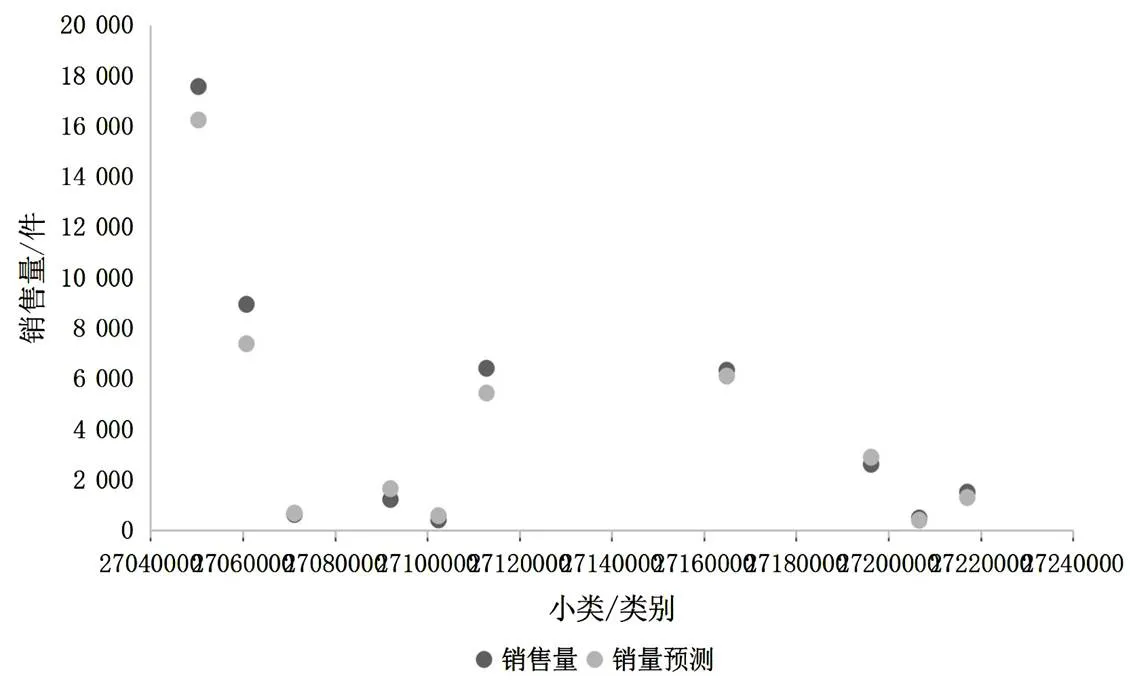
图3 12月份实际销售量与预测销售量对比

5 结论

本文通过平均绝对百分比误差法证实该主成分多元模型的可靠性，并可用于零售行业销量的预测。随着消费市场的不断发展，企业的零售产品越来越趋向多样化与个性化，针对多样化与个性化的模型将对这类行业大有用处。

［1］何汝群.珠江-西江经济带城市经济活力评价研究［D］.桂林：广西师范大学，2019.

［2］梅学聃，周梅华.有限时间数据下的零售药店药品销量预测研究［J］.中国矿业大学学报（社会科学版），2020，22（3）：133-144.

［3］杨维中.SPSS统计分析从入门到精通［M］.北京：清华大学出版社，2019.

［4］江艳婷，刘玉琬.基于IOWA算子的我国社会消费品零售总额的组合预测［J］.价值工程，2020，39（7）：54-56.

［5］杨冰融.基于多元线性回归与BP神经网络的乘用车市场预测模型［D］.武汉：华中科技大学，2017.

［6］张帆.基于商品品类的零售供应链需求预测与库存管理模式研究［D］.成都：电子科技大学，2011.

［7］叶欣.淘宝集市店铺手机销量影响因素分析［D］.北京：中国社会科学院研究生院，2018.

［8］王正军，刘光健，吕明，等.十堰市2000—2007年抗抑郁药年销量变化相关因素多元线性回归分析［J］.中国医院药学杂志，2009，29（1）：80-83.

［9］崔田.基于网络搜索数据的品牌汽车销量预测研究［D］.西安：西安理工大学，2019.

［10］周洁.基于时间顺序预测技术的“马钢”销售量与配车次数分析［J］.科技经济市场，2020（3）：7-9.

［11］曹晗.基于深度学习的餐饮业菜品销量预测研究［D］.西安：西安理工大学，2019.

F224

A

10.15913/j.cnki.kjycx.2020.18.013

2095－6835（2020）18－0034－05

吴琳洁（1998—），女，广东潮州人，本科。郑钰洁（2000—），女，四川成都人，本科。范云飞（2000—），男，广东广州人，本科。

〔编辑：严丽琴〕