基于matlab 动力配煤神经网络优化研究

张启明,李 贞

1.宁波职业技术学院,浙江 宁波 315800

2.岳阳职业技术学院,湖南 岳阳 414015

动力配煤是在煤炭入炉前，将各种不同种类的原煤按照一定的比例配制成品位高污染低的混煤的过程，通过动力配煤不仅可以节约煤炭资源，又能减小环境污染[1]。动力配煤作为一项节能、环保的洁净煤技术，具有极其显著的社会和经济效益，得到了国内外众多企业和学者的青睐，在我国也特别适应于国家大力提倡的节能环保技术开发及应用的基本国情[2]。动力配煤技术优劣主要由其配煤方案决定，配煤方案越优化，其配煤技术越高，产生的社会及经济价值巨大[3]。常用动力配煤优化方法一般可以分为综合模糊评判法、基于煤质数据分析的数学法、线性规划法、物理规划法及非线性理论规划法等[4]。

在综合模糊评判法中，由于不同种类的原料煤其特性不同，它们混合后不同种类煤颗粒在燃烧过程中相互制约和相互影响，很难通过该方法对其经济效益及环保特性进行准确的计算和评估[5]。基于煤质数据分析的数学法虽然能较准确的表示煤炭燃烧过程中煤质之间的相互关系，但是由于其目标函数为单方面的唯一值与实际煤炭企业实际生产情况存在一定的差异[6]。线性规划法、物理规划法等方法对动力煤方案优化也各有优势及特色，但其目标函数与基于煤炭数据分析的数学法一样存在一定的差异，因此其根据现场实际生产情况进行应用[7]。非线性理论规划法能够较为贴近实际煤炭企业动力配煤生产情况，通过神经网络可以较精确的预测动力煤燃烧特性的精度，为动力煤优化方案改进与预测精度的提高提供重要的保证[8]。基于此文以非线性理论模型为基础，运用RBF 神经网络建立动力配煤数学优化模型，对动力配煤燃烧特性进行仿真计算与预测，为动力配煤优化方案的改进与计算效率及精度的提高提供的重要的参考。

1 RBF 神经网络算法及动力配煤数学优化模型

1.1 RBF 神经网络算法

RBF 神经网络是一种高精度神经网络，该计算模型能够以任意精度对任意连续函数F(x)进行逼近，即：F(x)=WTJ(x)+ε(1)

式中：x∈Ʊ⊂Rn为神经网络模型中的输入向量；Ʊ为数集Rn上的子集；n为x的维数；ε为神经网络的逼近误差且满足|ε|≤εm，其中εm为逼近误差的限定值；W∈Rl为神经网络模型理想权值向量；l为神经网络隐含层神经元节点数；J(x)为神经网络模型中的的基函数向量。

本文选用高斯函数作为基函数：

式中：u为高斯函数J(x)的中心值；σ为高斯函数J(x)的宽度值；WTJ(x)为神经网络模型的输出值，W的值很难准确计算得到，用Wg表示W的估计值，则W的表达式为：

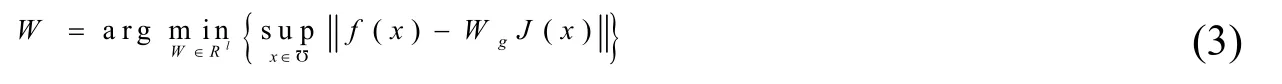
由于RBF 神经网络具有较好的逼近能力，RBF 神经网络模型被广泛用于各种工程逼近非线性特性和未知项的应用中。本文运用RBF 神经网络减小模型中的各其他的因数对神经网络系统的影响，从而提高模型计算及预测精度，提高动力配煤方案的优化。

1.2 动力配煤数学优化模型

动力配煤主要有配煤着火温度、活化能、最大燃烧速度、固定碳燃烬率及煤焦分形维数等。根据质量作用于物体上的定律结合arrhenius 方程，动力煤非等温热试验的反应速率为：

式中：α为热反应速率；m为热反应的级数；ξ为频率因子；E为热反应活化能；r为气体常数；t为热反应时间。

根据Doyle 单曲线法可得，动力煤燃烧反应式为：

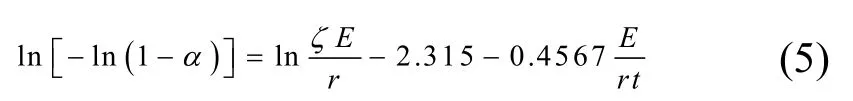
动力煤最大燃烧速率定义为DTG 峰值附近的80 ℃温度区内的动力煤样的最大平均燃烧速度值。固定碳燃烬率表示的是原煤中固定碳的燃烬特性，根据动力煤燃烧前后灰分子质量守恒可得固定碳燃烬率v为：

式中：mq为动力原煤试样在燃烧前质量；mh为动力原煤试样在燃烧后质量；G0为动力原煤试样在燃烧前固定碳工业分析值；H0为动力原煤试样在燃烧前灰分的工业分析值；Gmax为动力原煤试样最大燃烧失重率（包括水分、挥发分和己燃的固定碳）。

根据氮气吸附法可以求得表示煤炭固体表面结构特征的煤焦分形维数D：

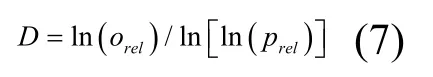
式中：Orel为动力原煤试样相对吸附量；prel为动力原煤试样相对吸附压力。

2 RBF 神经网络动力配煤优化及其应用

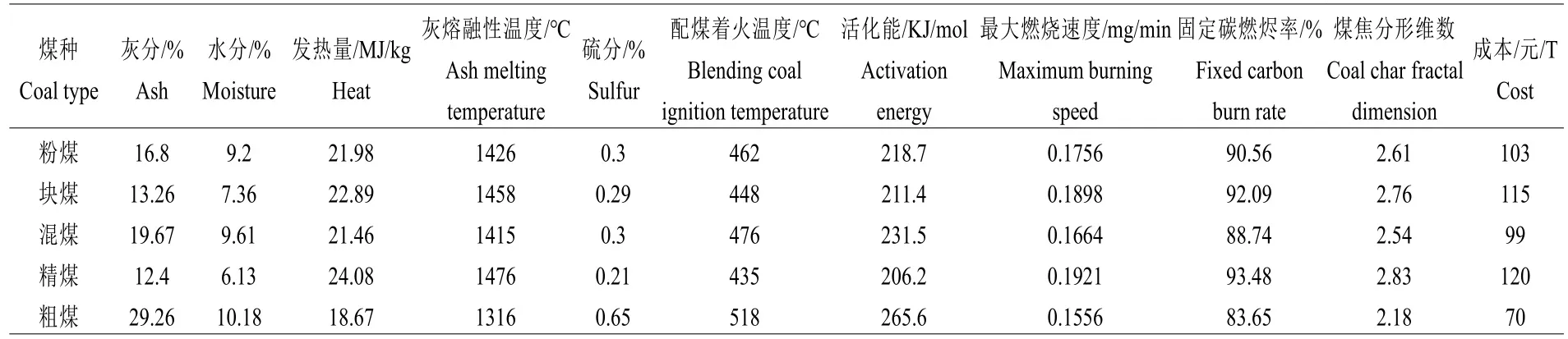
表1 动力配煤优化方案的原料煤基础数据Table 1 The raw coal basic data for the optimization scheme of power coal blending

以河南鹤壁某煤业集团动力配煤生产的实际情况为计算实例，设定神经网络的模型预测配煤精度为98%，将上述基于RBF 神经网络建立动力配煤数学优化模型，动力配煤优化方案的基础数据如表1 所示。

由表1 可知，动力配煤由粉煤、块煤、混煤、精煤、粗煤5 种原料煤组成，根据表1 的数据，得到包含灰分、水分、发热量、灰熔融性温度、硫分、配煤着火温度、活化能、最大燃烧速度、固定碳燃烬率、煤焦分形维数、成本等11 个主要动力配煤因数在内的动力配煤RBF 神经网络模型如下图1 所示。

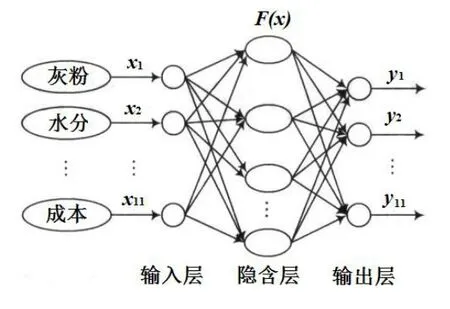
图1 动力配煤RBF 神经网络模型Fig.1 RBF neural network model of power coal blending

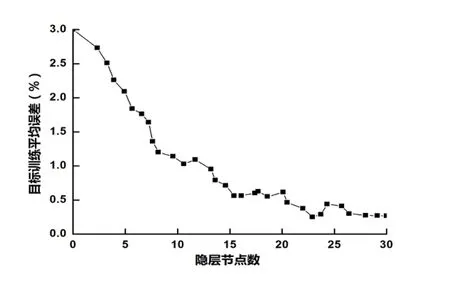
图2 隐层节点对RBF 神经网络平均误差的影响Fig.2 The effect of hidden layer nodes on the average error for RBF neural network

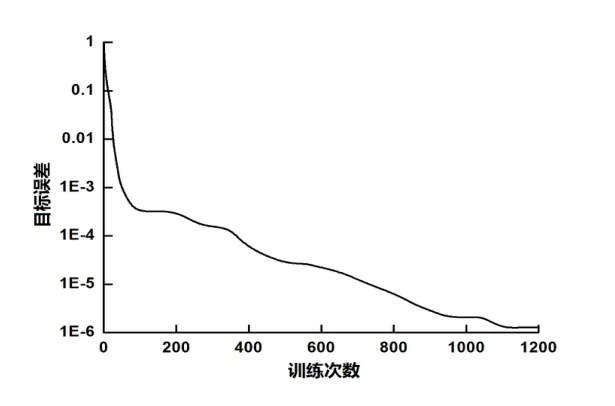
图3 训练次数对RBF 神经网络误差影响Fig.3 The influence of training times on the error for RBF neural network

根据上文及图1 中参数建立的动力配煤RBF 神经网络模型其目标训练平均误差与隐层节点数之间的关系曲线及目标误差与训练次数之间的关系曲线分别如图2、图3 所示。

根据上文基于RBF 神经网络建立的动力配煤数学优化模型，设置神经网络目标误差为1E-5，选取隐层节点为23 个，网格训练次数为800 次等参数。计算得到上述灰分、水分、发热量、灰熔融性温度、硫分、配煤着火温度、活化能、最大燃烧速度、固定碳燃烬率、煤焦分形维数、成本等11 个综合指标下的动力配煤配比量最优方案如下表2 所示，根据表2 得到的配比量得到最优动力配煤性能指标如表3 所示。

表2 运用RBF 神经网络动力配煤优化模型计算得到的动力配煤优化方案Table2 OptimizedschemeofpowercoalblendingcalculatedbyusingRBFneuralnetworkpowercoalblendingoptimizationmodel

由表2 可知，粉煤、块煤、混煤、精煤、粗煤5 种不同原料煤的灰分、水分、硫分等占比量不同，其在地层中煤焦分形维数也不同，从而导致其发热量、灰熔融性温度、配煤着火温度、活化能、最大燃烧速度、固定碳燃烬率等煤炭性能参数不同，煤炭在燃烧过程中产生的有害物、产热量及煤炭价格也不同。精煤燃烧性能最优，块煤次之，粉煤略低于块煤，混煤略低于粉煤，粗煤性能最差。为了获得组成成分满足现代节能环保的要求，燃烧特性最优、成本最低，需要根据动力煤的众多因数进行综合性考虑及优化，从而获各方面性能都优良的动力煤。根据表1 的参数结合上文中建立的数学模型计算得到粉煤、块煤、混煤、精煤、粗煤5 种不同原料配比而成的价格最优、燃烧特性较好、组成成分较佳煤的配比量分别为20.65%、18.12%、21.05%、18.30%、21.88%，在该配比下获得动力煤最优配煤方案。

表3 最优动力配煤性能指标Table 3 Optimal power coal blending performance index

由表3 可知，最优动力配煤成本在100.56 元/T，价格低于精煤价格20 元，获得仅次于精煤燃烧特性、组成优于混煤的新煤种。通过对动力配煤防范进行优化，不仅可以获得性能优良的煤种，同时也为煤炭燃烧过程中有害物资的排放、燃烧效率的提高，性价比的提升及环境保护提供了重要的保证。但是由于本文研究方案主要以价格、燃烧特性两个为主要指标，组成成分为次要因数获得的最优动力配煤方案，对于其他指标及原煤组成物不同，其动力配煤优化方案不同，且获得的最优动力配煤方案由于计量测量存在的误差，环境温度、湿度的改变等众多因数的影响，可能导致实际配煤方案与理论配煤方案存在一定的误差，实际动力配煤质量需要煤场自动在线检测设备进行复核，根据实际检测结果对实际配比实时进行调整，获得最佳动力配煤。

3 结论

基于RBF 神经网络算法建立包含灰分、水分、发热量、灰熔融性温度、硫分、配煤着火温度、活化能、最大燃烧速度、固定碳燃烬率、煤焦分形维数、成本等多因数非线性动力配煤的数学优化模型，获得用户期望的动力配煤优化方案，模型考虑煤质组成、燃烧特性、成本价格、地质分布情况等多种因数，应用于实际动力配煤生产中，该模型方案不仅能够获得性能优良的煤种，而且可以根据用户的实际需求，调整模型参数，更好反映和满足用户的真实需求及目的。