水工隧洞灌浆圈耐久性数值模拟
殷子文 张继勋 王 睿
(1.河海大学 水利水电学院, 南京 210098;2.深圳市水务规划设计院股份有限公司, 广东 深圳 518000)
在隧洞的开挖过程中,围岩应力重新分布,岩体将产生变形和破坏,为增强围岩的整体性、抗渗性,需对其进行灌浆处理.已有许多工程实例表明,灌浆工程运行数年后发生损坏甚至完全失效在所难免.灌浆圈的耐久性关系到水工隧洞的稳定运行,提前预测灌浆的有效防渗年限或其可能的损坏程度,对确保工程安全至关重要[1].
近年来,已有许多学者进行了灌浆耐久性方面的研究,赵莽[2]等以优选偏高岭土材料为研究对象,评价了干湿循环条件下龙门石窟灌浆材料的耐久性;张贵金[3]等认为优良的设计施工质量可以消除工程水文地质条件对灌浆耐久性的不利影响;闫福根[4]针对灌浆孔地质信息认识不足等情况,建立了灌浆统一数学模型;陈小勇[5]考虑地下水的影响,建立与实际相符的左右坝肩渗流模型,确定了水库运行的最优帷幕深度.但甚少有学者考虑多场耦合下的灌浆耐久性问题,徐建伟[6]等虽建立了渗流场和化学场的耦合模型,但却未能给出灌浆帷幕正常工作年限的判断.鉴于此,本文为模拟灌浆结石体在地下水环境中的实际情况,在研究了灌浆圈失效机制的基础上,拟采用渗流场、溶解沉淀场和溶质运移场的耦合来实现灌浆失效的过程.利用COMSOL Multiphysics有限元软件建立多场耦合数学模型,求解偏微分方程组,并在此基础上分析钙离子浓度、氢氧化钙质量分数以及灌浆圈耐久性.
1 灌浆圈失效机制及判据
深埋水工隧洞处于高地温、高渗透压力、高地应力以及复杂的水化学环境中,在多物理场作用下,灌浆结石体受到化学溶液的侵蚀,使得其颗粒之间的粘结作用减弱.同时,地下水对结石体存在溶蚀作用,伴随着流动将会带走溶蚀物质或产生吸附沉淀,导致灌浆结石体的结构发生显著改变,从而使得灌浆的抗渗能力大为降低,损害灌浆圈的耐久性能[7].
盛金昌[8]等通过裂隙岩体的应力-渗流-化学耦合渗透试验发现,化学反应将会加剧岩体裂隙的渗水量,且会促进溶解作用,引起渗流通道的改变[9].在水利工程中,常用的灌浆材料为水泥基材,渗透水可能会使水泥浆结石发生化学侵蚀,有些灌浆也有发生生物侵蚀的可能,这是由于含钙有机物产生适量气体溶解在水中而导致的.地下水对灌浆结石体的侵蚀作用以溶出型侵蚀的表现最为明显,其他类侵蚀均是不同程度的促进溶出型侵蚀,最终都加快钙离子从水泥结石中的溶出进程[1].判断溶出型侵蚀主要是依据Ca(OH)2的溶蚀量,因其在水泥的水化产物中最易被溶解,溶出的氢氧化钙将会与水流中的某些离子发生反应,达到促进或减缓溶解的效果,当溶液中的Ca(OH)2达到极限浓度时,溶解才会停止.然而,灌浆圈在地下水环境中受到内水压力和外水压力的双重作用,产生水力梯度,存在渗流场,渗透水流会不断地带走溶解出的Ca(OH)2,致使其浓度难以达到能够使水泥结石体稳定存在的浓度,固体氢氧化钙将会继续溶解加以补偿,随着时间的推移,逐步引起其他水化物如水化硅酸盐和水化铝酸盐的分解,渐进地腐蚀结石体,进而使结石体强度降低直至发生破坏.与此同时,研究显示[10],当水头较高时,结石体的透水性会增大,腐蚀现象更严重,溶蚀耐久性将会明显降低.
针对灌浆圈失效判据的选择,许多学者采用原苏联学者莫斯科文[11]的研究成果,即通过试验确定结石体的强度与CaO累计溶出率的关系,随着CaO累计溶出率的不断增加,灌浆结石体的强度将会降低,当累计溶出率达到25%时,结石体的强度急剧降低至初始值的50%,此时认为灌浆圈已经丧失了维持围岩整体性和稳定性的能力,灌浆失效.本文以此为依据,经简化,假定灌浆圈的析出物为Ca(OH)2,当固体氢氧化钙的质量分数达到75%时,认定灌浆结石体不足以继续承受压力.
2 多物理场耦合数学模型
2.1 渗流场
假定水工隧洞的洞段岩体为等效连续介质,因其位于地下水位以下,采用饱和流,渗流服从达西定律,可用以下模型[12]来描述:

其中:H为水头;kx、ky分别为x、y方向上的渗透系数;Ss为贮水率;初始条件h0(x,y)为水头的已知函数;水头边界条件h1(x,y)和流量边界条件q2(x,y,t)均为已知函数,Γ1和Γ2分别为已知的水头边界和流量边界,n为Γ2的外法线方向.
贮水率Ss的表达式为:

式中:ρ为水的密度;θ为围岩的孔隙率;α为固相压缩系数;β为水的压缩系数.
2.2 溶解沉淀场
溶质在多孔介质中存在各种物理、化学以及生物过程,通过这3种过程进行迁移和转化,从而实现时间、空间以及总量上的重新分布.其中化学过程主要包括吸附与解吸附、溶解和沉淀、氧化还原等作用,在控制方程的推导过程中,只能从主要因素出发,选取对结果影响最大的环节.本文参照徐建伟等的研究成果[12],将渗流对灌浆结石体的溶蚀描述为:

式中:F为固相溶质的质量分数;S为溶解沉淀速率参数;C为溶质的浓度;Kd为分配系数;F0(x,y)和G0(x,y)分别为质量分数的初始值和初始时间导数,均为已知函数.
2.3 溶质运移场
灌浆结石体中溶解出的Ca2+的运移可借鉴多孔介质污染物迁移动力学[13]的原理来描述,溶质在多孔介质中的迁移十分复杂,涉及多种因素的影响,本文仅考虑物理作用,即对流作用和水动力弥散.在溶质运移场中,采用对流-弥散方程,并将溶解沉淀产生的溶质通量作为源项加入其中,即:
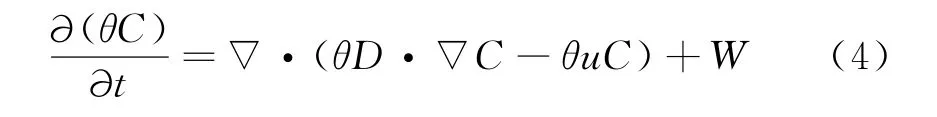
式中:D为水动力弥散系数张量,由下式给出:

式中:αT为横向弥散度;αL为纵向弥散度;δij为Kronecker函数;u为渗透速度;D*为分子扩散系数;τ为多孔介质的弯曲率.
W为源项,假设仅考虑固-液吸附过程,忽略固相内部质量的改变,则W=-f,-f为液相中溶质被固相吸附而减少的质量.固相上质量平衡方程可表述为:
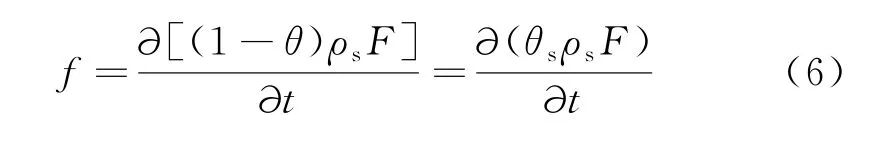
式中:F为单位固体质量上的溶质质量;ρs为固体密度;θs=1-θ为固体体积分量.
由上述可得溶质运移场的方程和定解条件为:
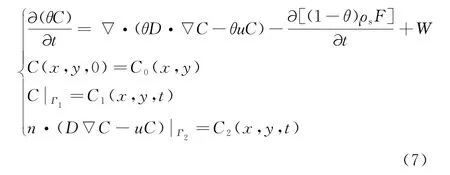
式中:C0(x,y)为浓度初始值,为已知函数;浓度边界条件C1(x,y,t)和溶质弥散通量边界条件C2(x,y,t)均为已知函数,Γ1和Γ2分别为已知的浓度边界和溶质通量边界,n为Γ2的外法线方向.
2.4 渗流场-溶解沉淀场-溶质运移场耦合
为实现水工隧洞灌浆圈的耐久性分析,通过COMSOL Multiphysics有限元软件建立了渗流场、溶解沉淀场和溶质运移场的多场耦合模型,即以各场控制方程的交叉参数和变量耦合实现对真实环境的模拟,进而研究在水压力的作用下,灌浆圈溶质的运移和溶解沉淀随时间的变化情况,耦合关系如图1所示.其中,由渗流场方程(1)计算所得的达西速度场将影响沉淀场(3)和运移场(7)中溶质的浓度变化,而(3)计算所得的溶质通量将作为源项加入(7)的对流-弥散方程中,同时,(7)的溶质浓度将影响(3)中的反应速率.最终通过方程的联立求解,实现场之间的相互作用.

图1 耦合作用示意图
3 水工隧洞灌浆圈耐久性算例分析
3.1 工程概况
某西南大型水电站为高水头、大容量、长隧洞的引水式电站,需开挖4条洞径为12.3~14.7 m,长度为16.7 m左右的引水隧洞,其平均埋深为1 500~2 000 m,最大埋深达2 525 m.由于受复杂地形和其他多种因素的影响,该隧洞面临高外水压力和高地应力等问题.本文选取该水电站1号引水隧洞的典型断面,进行运行期灌浆圈的耐久性分析.
3.2 计算模型和参数
断面围岩为Ⅲ类岩体,开挖洞径12.4 m×12.4 m,灌浆圈厚6 m,为分析模型中不同位置处的溶蚀情况,在断面上布设相应监测点,监测点坐标见表1,典型截面如图2所示.

表1 监测点坐标
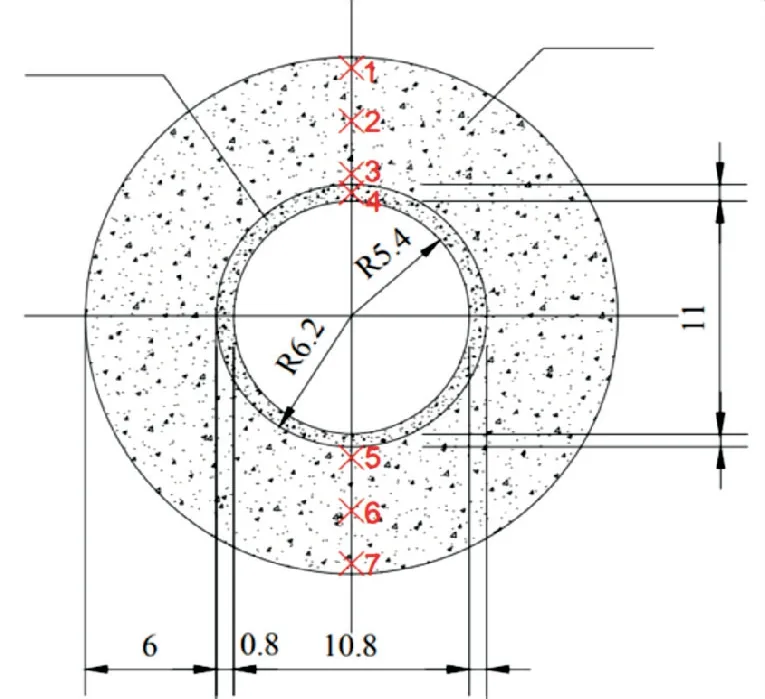
图2 模型计算区域几何尺寸图(单位:m)
该断面埋深1 300 m,研究区域取四面边界均距隧洞中心62.2 m的范围,远大于3倍洞径.模型参数的取值见表2和表3,其中,α为固相压缩系数;β为水的压缩系数;D*为分子扩散系数;αT为横向弥散度;αL为纵向弥散度;M为Ca(OH)2的摩尔质量;Kd为分配系数.对模型进行网格剖分,灌浆圈处采取加密处理,共生成3 520个单元,有限元网格如图3所示.本文以0.05年(记为0.05 a)为时间步长,100 a为总时间进行耦合计算,模拟了随时间变化下灌浆圈在计算域内与地下水溶液进行物质交换的动态过程.

表2 材料参数

表3 物理场计算参数

图3 模型计算区域有限元网格图
3.3 计算结果分析
3.3.1 Ca2+浓度
由图4可以看出,计算域内远离灌浆圈的溶液中,Ca2+浓度较低,故监测点主要布置在隧洞灌浆的周边区域.靠近洞周的拱顶部位钙离子浓度最高,100 a时其质量浓度的最大值为8.6 kg/m3.流速分布显示出地下水在内外水压力差的作用下,从四周围岩向隧洞内部渗透,渗流速度由隧洞周边向外逐渐减小.在隧洞周围的垂直方向上,拱底的渗透速度最大,拱顶的最小,这是不同的水压力差大小所致,而在水平方向上,渗流速度大致沿隧洞中心线成左右对称分布.渗流场的分布,一定程度上影响了Ca2+浓度的分布情况,拱顶的Ca2+浓度大于拱底,因拱底的对流作用强于拱顶,析出的Ca2+被水流带走,向隧洞内扩散,而隧洞左右两侧的Ca2+浓度大致呈对称分布,与渗流速度的分布规律相符.
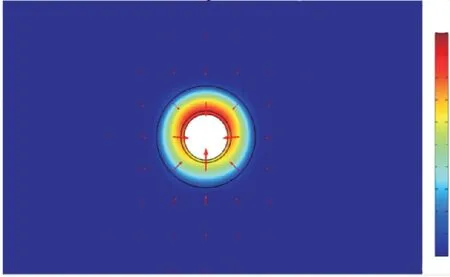
图4 100 a时Ca2+浓度分布及渗流速度矢量图
图5显示了不同监测点Ca2+的浓度变化,考虑到在0.5 a前Ca2+的浓度变化较大,且在0.5 a时达到最大值,后期的变化速率相对平缓,故在对比中选用不均匀的x轴来展现随时间变化下的浓度变化情况.监测点3的Ca2+浓度最大,该测点位于灌浆圈内部,衬砌中的监测点4的Ca2+浓度与之相近,且浓度具有向隧洞外逐渐降低的趋势.初期各监测点的Ca2+浓度均迅速增加,后经过一段时间的缓慢增长达到最大值,随之浓度开始逐渐降低.这是由于初始阶段溶液中氢氧化钙的浓度与其使水泥结石体稳定存在的浓度相差较大,固相氢氧化钙迅速溶解,此时的溶解作用大于对流作用,Ca2+浓度保持升高的状态,当浓度升高至某一临界值时,对流作用开始占主导地位,虽然此时氢氧化钙持续溶解,但Ca2+被渗透水流带走的速度大于溶解速度,导致溶液中Ca2+的浓度开始降低.

图5 不同监测点钙离子浓度变化
3.3.2 Ca(OH)2质量分数
100 a时固体氢氧化钙质量分数的分布如图6所示,其质量分数已从初始状态的1衰减到约0.7左右,且拱底部位的溶蚀量要高于拱顶.

图6 100 a时固体氢氧化钙质量分数分布图
产生这种现象主要归结于渗流场的作用,拱底的渗流速度较大,溶解出的Ca2+被迅速转移,溶解沉淀平衡被打破,从而促进了固相氢氧化钙的进一步溶解.图7显示了各监测点上氢氧化钙质量分数的变化情况.可见,由于在运行期内隧洞水压力差的作用下,地下水流通过岩体介质的空隙、节理等进入灌浆圈,并与之发生一系列的化学反应,导致化学元素的位置发生了重新分配,具体表现为在模拟运行期100 a内,灌浆圈中氢氧化钙的质量分数随时间不断减少.在渗流场的作用下,水流不断地与周围介质发生化学反应,改变了灌浆结石体的细观结构,使得其在运行过程中性能逐渐劣化直至最终失效.可以认为,灌浆结石体的老化就是水-岩的化学相互作用而导致的结果.

图7 不同监测点氢氧化钙质量分数变化
将灌浆圈内的3个监测点依次相连构成一条监测线,图8为监测线上氢氧化钙质量分数的变化情况.由图可知,灌浆圈的溶蚀量和溶蚀速度均由外部向内部递减,且时间越长,内外的溶蚀量差值越大.这是因为灌浆圈外侧靠近围岩,围岩的孔隙率较大,储存和运输的地下水较多,渗流对溶蚀作用产生了促进的影响,而灌浆圈内部以及衬砌中的水流相对较少,其溶蚀作用低于外部.由以上分析可知,灌浆圈外部和拱底处均为薄弱区,易因溶蚀而降低灌浆圈的强度、防渗性和耐久性,使灌浆圈失效,故在设计中应采取相应的措施予以加固.

图8 监测线氢氧化钙质量分数变化
3.3.3 灌浆圈耐久性
本文拟采用前述的灌浆圈失效判据,认为当固体氢氧化钙的质量分数达到75%时,灌浆结石体不足以继续承受压力.考虑到灌浆圈各部位的溶蚀量并不均匀,且由前述内容可知,灌浆圈外部和拱底处的溶蚀量较大,为薄弱地带,故以其相应关键点处的溶蚀量判断灌浆圈的耐久性.

图9 灌浆圈关键点氢氧化钙质量分数变化
由图9可知,监测点7处将最快达到失效临界点,由数据内插可得64 a时该处氢氧化钙的溶蚀量达25%,即灌浆圈的有效运行年限为64 a,此后各部位的强度将逐渐降至初始值的50%,须及时采取补灌等工程措施.
4 结 论
本文在研究了水工隧洞灌浆圈失效机制的基础上,建立了多物理场耦合数学模型,对灌浆圈在运行期内的钙离子浓度、氢氧化钙质量分数以及其耐久性进行了分析,得出以下结论:
1)由于物理场之间的相互作用,灌浆圈在整个模拟运行期内,固相氢氧化钙会不断溶解,无法达到平衡状态.且各部位的溶蚀程度有所差异,以灌浆圈外部和拱底处最为严重,是灌浆质量控制的重点区域,应及时采取有效措施予以加固.
2)模拟过程中钙离子浓度的变化规律和氢氧化钙质量分数的变化相互照应,体现了在渗流场作用下二者相互促进的结果.这说明耦合模型可以较为真实地反映水工隧洞灌浆圈长期处于地下水环境中的破坏规律,适用于对其耐久性的分析中.
3)采用经典的灌浆失效判据,并进行了相应的简化,没有考虑化学作用中具体的离子反应,通过Ca(OH)2质量分数的变化,进行了灌浆圈的耐久性评价,以此判断算例中水工隧洞灌浆圈的正常工作年限为64 a.

