弱观测条件下纯距离导航定位问题研究

冀大雄 邓啸

摘  要：水下无人潜航器（Underwater Unmanned Vehicle，UUV）的导航定位主要依靠测距声信标或便携式低精度导航传感器。这些设备观测信息单一且精度低，载体非线性运动及复杂海流等因素均对导航定位精度有较大的影响。因此，文章设计了基于扩展卡尔曼滤波（Extended Kalman Filtering，EKF）的导航算法，结果表明该算法适用范围广且具有好的收敛性和精度。

关键词：水下潜航器;导航定位;扩展卡尔曼滤波

中图分类号：TN966     文献标识码：A

Abstract：The navigation and positioning of underwater unmanned vehicles（UUV） mainly relies on the ranging acoustic beacon or portable low-precision navigation sensor.The observation information of these devices is single and the accuracy is low.The nonlinear motion of the carrier and the complex ocean currents have a great influence on the navigation and positioning accuracy.Therefore，a navigation algorithm based on extended Kalman filter（EKF）is designed in this manuscript.The results show that the algorithm has a wide range of applications and good convergence and accuracy.

Key words：Underwater unmanned vehicles;Navigation and positioning;Extended Kalman filter

水下无人潜航器（UUV）具有隐蔽性好、综合效益高等优点，已在多个领域得到了发展和应用[1]。UUV协同探测能够完成单UUV很难完成或无法完成的任务，发挥更大的作用[2]。UUV面临的主要瓶颈是水下导航系统的设计，该系统要能精准定位并提供速度、姿态等信息。同时，受质量、体积限制及水介质等多种因素影响，UUV的精确导航仍然是该领域内的难点[3]。

传统的导航方法是以航位推算为基础，将多普勒测速仪和惯性导航系统融合，但误差会随时间积累而越来越大。EKF导航算法是一种基于模型近似线性化和高斯假设的次优滤波法[4]。曹方方等利用EKF算法估计出UUV相对信标的位置，通过优化算法，可有效降低定位过程中的累积位置误差，设计的水下航行体导航定位系统，利用卡尔曼滤波与GPS异常点剔除算法，提高了自动控制实时性且增强了航迹控制精确性[5]。笔者基于EKF算法，通过分析和实验证明了其可应用于三信标、固定单信标和移动单信标三种条件下的UUV导航定位场景，同时航位估计和水流估计精度很高。

一、载体非线性运动模型

首先建立东—北直角坐标系EON，然后以载体重心G为原点建立载体坐标系xOy，如图1所示。假设载体在海流速度为v的海水中沿水平面运动，并忽略横摇扰动的影响。另外，载体装备的电子罗盘能显示载体艏向角Ψ，装备的计程仪可计算出沿载体艏向的速度u。载体重心G的速度V可由海流与艏向速度的合成速度求得，载体ON向坐标轴的夹角称为记为γ，其物理含义是航迹角。海流作用使得载体以一定的角度航行，该角度记为β，名称为漂角。通过下式可以求得载体在水平面的艏向速度：

载体内安装有定位声呐测量载体，可以每隔一段时间，通过测量载体到声信标的声传播时间，求得距离，使载体在纯距离方式下导航。令为载体东—北坐标系下的坐标，为海流东、北向分量，为涡轮式计程仪测量的速度，和为载体的艏向角和纵倾角。对于携带压力传感器的UUV，仅需估计载体的二维坐标。考虑到涡轮式计程仪测量的是相对海流的速度，在导航算法中还应估计海流速度。因此，采用状态—参数联系估计，设滤波器状态为，对载体的非线性运动进行离散化，建立如下运动学微分模型：

剩下的问题是设计有效的导航算法，满足UUV在弱观测条件下的导航需要。文章采用基于Kalman滤波器的导航算法，根据声信标数量及运动状态，分成三种情况予以研究。

二、不同条件下的运动学分析

（一）三信标条件下的运动学分析

根据三圆交汇原理，当有距离信息到来时，代入定位方程解算载体位置。载体携带的导航传感器（电子罗盘和计程仪）和位置信息分别构成了两个线性化观测方程，分别由式（9）和式（10）表示：

（9）

（10）

其中，式（9）为沒有位置信息时的观测方程;式（10）为位置信息到来时的观测方程。

载体的全部运动过程由部分可观性动态系统和完全可观性动态系统组成。每隔固定时间载体更新一次位置信息，在固定时段内载体根据观测量速度和艏向推算航位，能够在时间区间段意义上，实现系统的完全可观。

（二）固定单信标条件下的运动学分析

单信标条件下载体不能直接得出自身的位置坐标。导航传感器更新率小于位置更新率，因此需要的观测方程有两个，即：

单信标条件下载体不能直接得出自身的位置坐标。载体的全部运动过程由部分可观性系统和完全可观性动态系统组成。每隔固定时间载体更新一次距离信息，在固定时段内载体根据观测量速度和艏向推算航位。将上述可观性动态系统和完全可观性动态系统组合起来，使载体机动航行（改变航向或航速非线性改变），能实现系统在时段区间意义上的完全可观。

（三）移动单信标条件下的运动学分析

移动单信标条件下载体不能直接得出自身的位置坐标。导航传感器更新率小于位置更新率，因此需要的观测方程有两个，同式（11）与式（12）。

移动单信标条件下载体不能直接得出自身的位置坐标。载体的全部运动过程由部分可观性系统和完全可观性动态系统组成。每隔固定时间载体更新一次距离信息，在固定时段内载体根据观测量速度和艏向推算航位。将上述可观性动态系统和完全可观性动态系统组合起来，使信标或载体机动航行（改变航迹），能够实现系统在时段区间意义上的完全可观。

（四）主从式多UUV群体的运动学分析

研究由一个主UUV和两个从UUV构成的主从式多UUV群体，如图2。主UUV与从UUV时间同步。主UUV携带高精度导航传感器，能够实时得到准确的地理坐标，具备自主导航能力。同时，主UUV还安装了水声Modem，将自身的实时位置数据定时发送给从UUV。从UUV携带低成本、精度较低的导航传感器，通过安装的水声Modem接收主UUV的位置数据，同时测量从UUV到主UUV的声传播时间以得到距离。

在这种模式下从UUV不能直接得出自身的位置坐标。导航传感器更新率小于位置更新率，因此需要的观测方程有两个，即

其他從UUV的观测方程同上。从UUV的全部运动过程由部分可观性动态系统和完全可观性动态系统组成。每隔固定时间从UUV更新一次距离信息，在固定时段内从UUV根据观测量速度和艏向推算航位。将上述可观性动态系统和完全可观性动态系统组合起来，使主UUV或从UUV机动航行（改变航迹），能够实现系统在时段区间意义上的完全可观。

三、导航算法

由于载体运动状态方程是非线性的，对于单信标（固定、移动、主从UUV）情况，观测方程也是非线性的，考虑到海流等参数，需要对状态和参数进行联合估计，因此采用基于EKF的导航算法。

（一）算法一

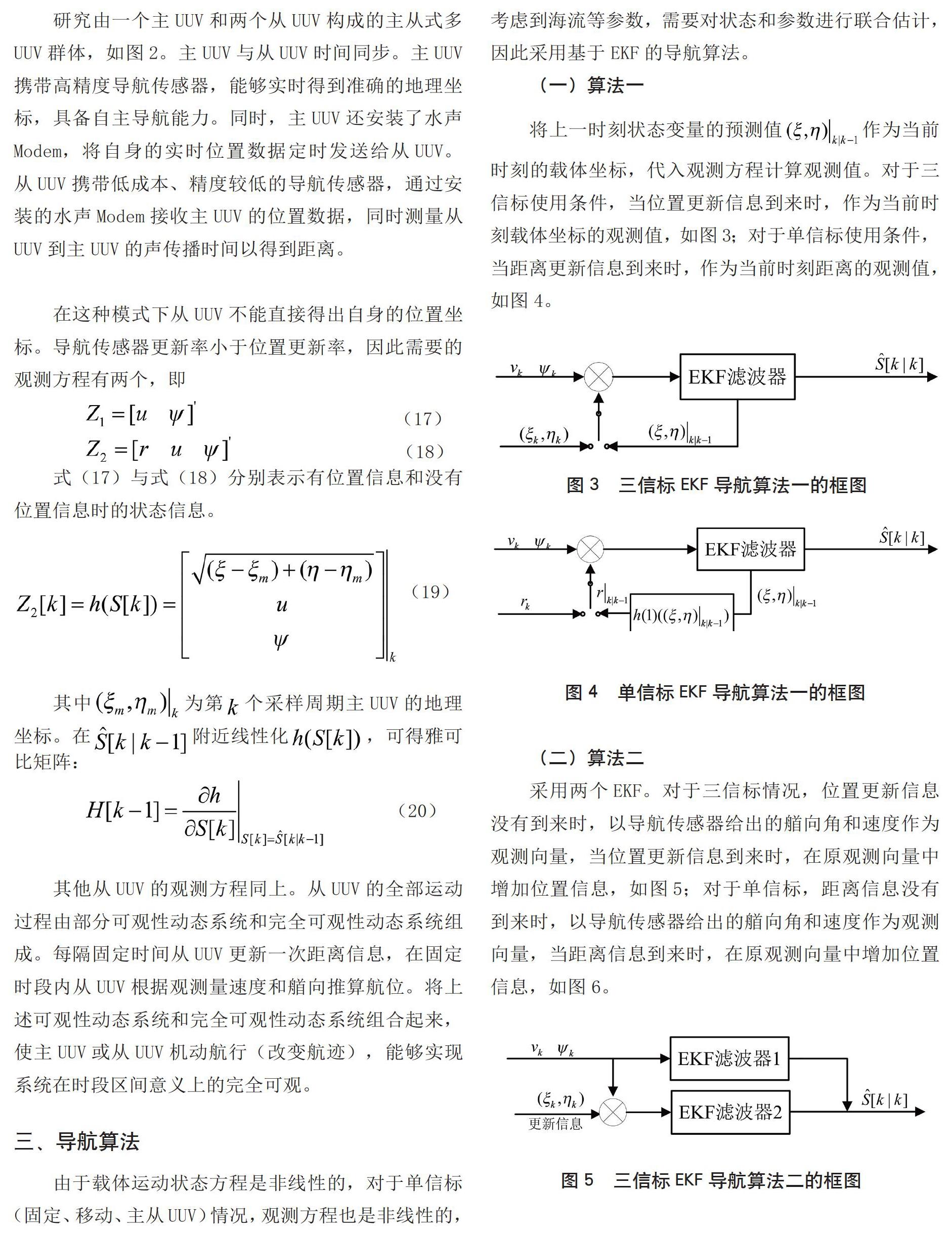
将上一时刻状态变量的预测值作为当前时刻的载体坐标，代入观测方程计算观测值。对于三信标使用条件，当位置更新信息到来时，作为当前时刻载体坐标的观测值，如图3;对于单信标使用条件，当距离更新信息到来时，作为当前时刻距离的观测值，如图4。

（二）算法二

采用两个EKF。对于三信标情况，位置更新信息没有到来时，以导航传感器给出的艏向角和速度作为观测向量，当位置更新信息到来时，在原观测向量中增加位置信息，如图5;对于单信标，距离信息没有到来时，以导航传感器给出的艏向角和速度作为观测向量，当距离信息到来时，在原观测向量中增加位置信息，如图6。

四、观测值的确定

（一）三信标

以载体位置、导航传感器给出的速度及艏向角作为观测值，根据声双程传播时间和平均声速计算载体到信标的距离，再利用声信标与载体的高度差计算水平距离，考虑到载体在传播时间内位置的偏移，将其全部代入定位方程，即可算出载体坐标。也可利用二次多项式法得到较高精度的水平距离。不管采用哪种方式，在声传播时间中都应减去信标的检测延时。

（二）单信标

载体到信标的水平距离、导航传感器给出的速度及艏向角作为观测值。在应答方式下，采用与三信标相同的方法得到载体到信标的距离和水平距离，再代入定位方程求解，也可利用二次多项式法得到较高精度的水平距离。不管采用哪种方式，在声传播时间中都应减去信标的检测延时。在同步方式下，根据声单程传播时间和平均声速计算载体到信标的距离，再利用声信标与载体的高度差计算水平距离，也可利用二次多项式法或本征声线法得到较高精度的水平距离。

（三）异常值剔除

采用马氏距离法判断距离测量值的野点，根据距离预测值与测量值的差确定异常点：

其中为第时刻的距离观测值，，是样本的协方差矩阵，是一个可调参数。当上式左边大于时，则该时刻距离测量值野点，予以剔除。

五、实验结果与分析

仅考虑载体在水平面内的运动状态。导航传感器误差服从零均值的高斯分布，计程仪与电子罗盘误差方差分别为5%和2°。载体坐标分量测量方差为1米，载体到信标的距离测量误差方差为1米。导航传感器数据更新率为1秒，位置或距离更新率30秒。海流分量从0.5米跳跃到0.8米，仿真时间3000秒。规定以与实际初始位置偏差50米的坐标分量作为状态分量初始值，其他状态分量初始值均为零。分别给出三信标（图7、8）、固定单信标（图9、10）、移动单信标（图11、12）、主从UUV（图13）条件下航位估计和水流估计的仿真结果。

六、结论

理论分析和仿真实验表明，EKF导航算法不仅能够应用于三信标条件下携带低精度导航传感器的UUV导航定位，同样适用于固定单信标和移动单信标条件下的导航定位，航位估计和水流估计精度很高。不同的是在三信标条件下载体不用机动航行，而单信标载体需要进行一定的机动航行，以提高系统可观测性。仿真实验表明设计的滤波器是渐进稳定的，也就是滤波性能不受初始值的影响，只要滤波时间足够长，总能以任意精度逼近实际值。仿真实验还表明导航算法二的滤波性能优于导航算法一，具有更好的收敛性和精度。

参考文献：

[1]金建海，陈伟华，张波，等.UUV集群技术概述[C]//中国造船工程学会，西北工业大学，中国船舶重工集团有限公司第七〇五研究所.2018年水下无人系统技术高峰论坛论文集.西安：《水下无人系统学报》编辑部，2017：92-96.

[2]周宏坤，葛锡云，邱中梁，等.UUV集群协同探测与数据融合技术研究[J].舰船科学技术，2017（12）：70-75.

[3]张立川，刘明雍，徐德民，等.基于水声传播延迟的主从式多无人水下航行器协同导航定位研究[J].兵工学报，2009（12）：1674-1678.

[4]刘国海，李沁雪，施维，等.动态卡尔曼滤波在导航试验状态估计中的应用[J].仪器仪表学报，2009（02）：396-400.

[5]曹方方，刘卫东，李娟丽.基于EKF的UUV单信标水声导航定位方法研究[J].计算机测量与控制，2011（09）：2234-2236+2244.

[6]张晋斌.基于卡尔曼滤波的UUV导航定位系统GPS异常点剔除方法[J].电子世界，2014（15）：95.