多视角几何三维重建法识别工程结构缺损与变形

刘宇飞，樊健生，孔思宇，魏晓晨

(清华大学土木工程系，清华大学土木工程安全与耐久教育部重点实验室，北京 100084)

结构表面缺损与构件变形是既有结构现场检测或长期监测的重要指标，也是安全性评估、鉴定的重要依据，典型如混凝土结构表面裂缝、漏筋，钢结构锈蚀、螺栓脱落，钢结构构件弯曲变形与板材局部屈曲等。在当前既有结构检测鉴定现场作业中：对表面缺损的检查仍依赖于人工接触式方法，操作费时费力，存在测不准、高空多、效率低、记不全等缺点，一方面检查精度与效率低下，另一方面人员作业安全风险难以控制；对构件变形的测量仍依赖于全站仪，难以实现空间变形的精准测量。采用数字图像法配合以智能的数字图像处理技术，可有效提升检查与检测的效率、降低作业风险，相关研究成为近五年的热点并逐渐实现工程应用。但是，工程实践中暴露出的问题，影响了数字图像检测技术的推广应用，如定量检测中图像几何变形修正困难、局部损伤难以在整体结构中定位、无法测量钢结构空间变形等。结合多视角几何三维重建法的研究与应用，可有效解决上述问题，提高数字图像法的适用性并扩展技术的应用场景。本文对多视角几何三维重建法识别结构表面缺损与变形的方法原理与技术创新进行研究与讨论。

1 多视角几何三维重建法

1.1 方法原理

多视角几何三维重建法(Multi-view geometric 3D scene reconstruction method, 常被简称为“多视”)利用数字图像进行表面三维场景重建，主要原理是基于机器视角的多视角几何方法[1−2]。其中，“多视角”表示图像获取的要求以及算法执行的假设：用于重建的图像必须在多个不同的摄影视角与机位下拍摄，图像互有重叠且重叠率不小于50%，环绕拍摄效果更佳。基于数字图像的多视角几何三维重建不依赖于物体原始的空间几何关系与相对尺寸信息，也无需成像时相机的空间位置与朝向信息，仅利用原始的数字图像与相机、镜头参数等信息，即可直接还原成像模型、生成相机空间参数与三维场景。因此，该方法具有硬件设备要求低、现场操作简便等特点。

多视角几何三维重建法的成功实现依赖于后期算法处理。首先，数字图像要经过图像畸变矫正(Image undistortion)完成预处理；在此之后，经过特征点识别(Feature extraction)、特征点匹配(Feature matching)、相机运动参数估计(Camera motion estimation)、模型优化(Model optimization)、稀疏点云三维重建(Sparse point cloud 3D reconstruction)等步骤，完成运动恢复结构(Structure from Motion,SfM)运算，获得相机空间参数及稀疏三维点云模型。在此基础上，利用获得的参数与模型，进行密集三维点云重建(Dense point cloud 3D reconstruction)，获取密集的三维点云模型。完整的多视角几何三维重建法步骤见图1 所示。

图1 多视角几何三维重建法步骤Fig. 1 Process of multi-view geometric 3D reconstruction method

多视角几何三维重建的核心算法是运动恢复结构运算，运动恢复结构运算的最重要功能是相机运动参数估计。事实上，多视角几何算法就是解决相机运动参数估计的方法，具体包括了双视角几何、三视角几何、以及多视角几何等不同情况，其中多视角几何问题可由双视角几何与三视角几何组合来解决。以双视角几何算法为例，待估计的计算相机内参主要包括基础矩阵(Foundation matrix)F与本质矩阵(Essential matrix)E，其中基础矩阵F描述了两个相机成像的极线约束关系，如图2 所示的约束三角关系。图2 中点O与点O′分别表示参与双视角几何计算的两个相机的空间位置，点A表示某个匹配的特征点对的实际空间位置，点a与点a′分别表示点A在2 个相机成像平面上的位置，采用薄透镜成像模型。由匹配特征点的空间位置约束可以求取基础矩阵F，数学关系的描述参见式1 所示。基础矩阵F共包括7 个待定参数，因此需要最少7 组匹配特征点方可确定F。式中，x与x′分别表示匹配特征点对的齐次像素坐标。

图2 双视角几何的极线几何约束关系Fig. 2 Polar line geometric constraint relationship of double-view geometry

本质矩阵E是基础矩阵F在图像坐标系归一化时的特征表达形式，可由式(2)进行计算：

式中，K与K′分别表示两个相机的内参矩阵。

基础矩阵F与本质矩阵E是连接匹配特征点到相机运动参数估计的桥梁，是双视角几何运算的核心变量。在三视角几何中，基础矩阵由三焦张量(Trifocal tensor)T代替。

1.2 算法实现

多种算法可实现多视角几何三维重建法。以特征点识别与匹配为例，经典方法是哥伦比亚大学David G.Lowe 教授提出的SIFT (Scale Invariant Feature Transform)[3]方法，其特征描述对图像的旋转、缩放保持不变，具备所谓的“尺度不变性”；在此基础上2012 年提出的KAZE 算子[4]拥有相对更高的匹配率与更好的识别效率。表1 列出了三维重建的4 个关键步骤的实现算法，包含了经典方法与相对更高效的方法。除利用表1 中的算法，基于数字图像的多视角几何三维重建可由多种开源或图形界面应用程序系统实现，如FIT3D toolbox[5]、VisualSFM[6−7]等。

表1 多视角几何三维重建的实现方法Table 1 Implementation methods of multi-view geometric 3D reconstruction

过去数十年中，基于数字图像与多视角几何的三维重建技术得到快速发展[1]，在土木工程领域的应用也逐渐被重视。以多视角几何为基本原理的倾斜摄影技术，在地表测绘与三维地理空间建模[13−15]领域得到广泛应用。由于三维重建技术不需要人工靶标或拍摄相机空间位置参数、可直接生成有一定精度的三维模型，在巨型建筑结构、基础设施的快速建模应用中表现出较大优势，典型应用包括城市三维数字建模[16]、施工现场精细管理[17]等。但是，在既有结构的损伤识别、检测与监测领域，多视角几何三维重建技术目前的应用研究较少，可见的文献报道主要集中于裂缝识别[18]等领域。

2 基于三维重建的损伤识别方法创新

采用多视角几何三维重建可以获取待测物体的表面点云模型以及图像拍摄时相机的空间位置与视角。利用上述信息，可完整恢复成像模型与场景，为基于数字图像法的结构表面损伤与变形的识别提供有力工具。

2.1 表面投影法解决成像几何变形与损伤定位

由成像原理和结构表面形状决定，成像于二维数字图像的结构表面缺损通常存在几何变形，影响数字图像法定量检测的精度。变形原因有两类：1)当拍摄方向或主光轴方向并非正对待测物体表面时，成像的物体呈现近大远小的透射变形；2)当待测物体表面几何形状非平面，成像后表面损伤会产生复杂结构表面投影的几何变形。上述成像几何变形会导致结构表面损伤的分布与形状发生变化。以图3 中裂缝损伤为例，示例1 中相机A为正对开裂平面的摄影，成像后的裂缝无明显变形，除此之外的相机B以及示例2-4 均存在透视变形；示例2-4 中的开裂结构表面分别为多个表面、曲面以及复杂表面，摄影图像中的裂缝会产生复杂几何表面投影变形。在裂缝识别中，这两类几何变形不仅影响对裂缝分布、形状的测量，也会影响对裂缝宽度与长度的准确计算。

图3 投影过程中的几何变形Fig. 3 Process of crack projection

另一方面，损伤识别精度与损伤定位的矛盾影响数字图像法检测的应用效率。当损伤识别精度要求较高时，通常采用近距离拍摄或使用长焦镜头，图像场景变小，难以定位损伤；当希望在全景图像或整体结构中定位损伤，又需要远距离拍摄或使用广角镜头，图像场景变大，但对损伤的分辨率降低、细微损伤无法识别。工程实践中，在对大体量工程结构进行数字图像法损伤识别，或使用高倍望远镜、长焦镜头拍摄损伤，单张图像所包含的场景远小于整体结构，均产生损伤定位困难的问题。倘若拍摄的图像中缺乏唯一性标记或未准确记录拍摄点轴线等位置信息，后期处理将无法生成损伤分布图，单纯基于二维数字图像法的损伤识别失去意义。

针对上述两种工程实践问题，结合三维重建模型与场景，提出基于成像原理的损伤投影方法，修正二维数字图像的倾斜与深度、完成几何变形的修正，同时实现损伤在整体模型中的定位[18]；具体地，采用多视角几何三维重建方法，完成结构表面的三维重建，获得三维点云模型，进一步拟合形成结构表面连续模型；利用多视角几何三维重建得到的相机空间参数(相机位置与朝向)，还原成像过程，逆向投影，将二维数字图像中识别得到的表面裂缝等损伤投影至结构表面连续模型中(如图4 所示)，将裂缝还原、标记于三维模型中，完成裂缝体的形态修正。如果投影过程采用了多视角几何三维重建的结构整体模型，可以实现损伤在整体模型中的准确定位，化解损伤识别精度与损伤定位的矛盾。进一步地发展损伤定位优势，集成硬件设备，可实现损伤的长期监测。上述操作中，二维数字图像的损伤识别可由数字图像处理方法或深度卷积神经网络方法实现。

图4 裂缝体投影过程Fig. 4 Process of crack projection

2.2 逆向工程建模与特征提取识别几何变形损伤

基于多视角几何三维重建获取的三维点云模型，经过逆向工程建模与特征提取，可实现构件几何变形损伤的定量检测。工程现场获得结构表面三维模型的方法有多种，表2 对包含多视角几何三维重建法在内的4 种获取三维表面模型的常用技术进行对比，对比内容包括技术原理、光源、精度、数据格式、现场操作时长、操作技能要求、设备成本等，结果表明，多视角几何三维重建法具有现场操作方便、操作技术要求低、设备成本低廉等优势，且相对而言精度满足工程要求，在工程实践中具有明显优势。

表2 获取三维表面模型的常用技术Table 2 Commonly-used techniques for obtaining 3D surface models

在获取稀疏或密集三维点云的基础上，进一步地，对点云执行降噪、抽稀操作，生成密度适中、精度高的精细点云模型之后，可进行三角形表面网格化建模以得到三角形表面网格模型。三角形表面网格化的重要作用是将离散的点云模型转化为连续的表面模型[19−20]，为后期三维模型的逆向处理提供重要素材。虽然直接重建得到的点云模型精度可能仅为厘米级，经抽稀、降噪、拟合后提取构件几何特征，精度可进一步提升，满足工程精度要求。

3 应用研究①：结构表面裂缝识别

3.1 结构表面裂缝识别

基于数字图像的结构表面裂缝识别是当前数字图像法检测应用的热点。采用基于二维数字图像处理与深度卷积神经网络可实现图像中裂缝的识别，结合第2.1 节表面投影方法可进一步解决成像几何变形问题。图5、图6、图7 分别展示了结构表面单个平面、结构表面多个平面以及结构曲形表面的裂缝投影示例，投影使用的裂缝图像为1 张或多张。利用上述方法完成裂缝投影后，可得到裂缝体在三维模型中的形态与参数，完成裂缝形态的修正以及裂缝在三维模型中的位置标记。进一步地，利用投影后的裂缝宽度特征点计算裂缝宽度，即可得到准确、无变形的裂缝参数。

表3 展示了图5、图6、图7 示例中共计11个测点的裂缝识别结果，与人工测量结果相比，裂缝宽度识别结果的误差在0%～33%，基本满足工程应用的需求。

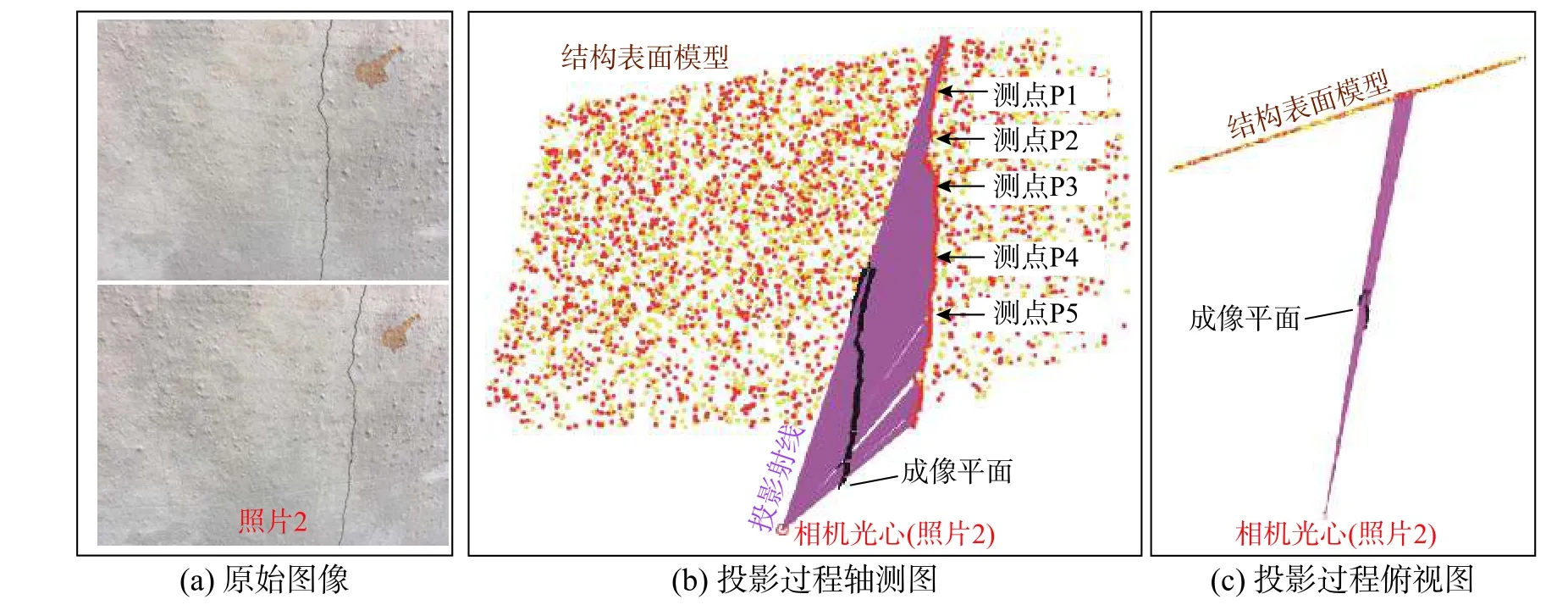
图5 裂缝投影至结构表面单个平面(试验T1)Fig. 5 Crack projection onto single plane of structural surface (Test T1)

图6 裂缝投影至结构表面3 个平面(试验T2)Fig. 6 Crack projection onto three planes of structural surface (Test T2)

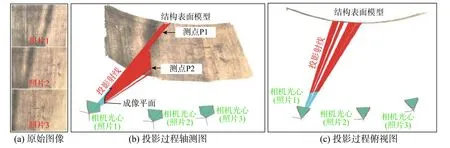
图7 裂缝投影至结构曲形表面(试验T3)Fig. 7 Crack projection onto curved structural surface (Test T3)

表3 裂缝宽度计算误差Table 3 Error of crack width calculation

4 应用研究②：大型构筑物表面损伤定位

大型构筑物以及桥梁、隧道、大坝、路面等工程结构的损伤检查中，单张照片中损伤定位的难度较大，采用第2.1 节表面投影方法可有效解决该问题。以某冷却塔外壁损伤识别为例，该冷却塔塔高70 m，淋水面积2000 m2，为小型自然通风淡水冷却塔，建于20 世纪70 年代末期，长期使用后塔筒混凝土出现严重的破损、漏筋等耐久性问题，现因改变使用需求须加固改造。结构安全性检查中，采用多视角几何三维重建方法，对塔筒外壁进行三维重建。图像拍摄使用佳能EOS 5D Mark III 相机，图像分辨率5760×3840。共使用58 张不同视角环绕拍摄的图像完成重建，得到的三维表面模型与成像时相机的位置朝向见图8、图9 所示，建立了各张图片与整体三维模型的对应关系，使得任何一张图片中标记出的损伤都可投影、定位于整体三维模型。本算例以塔外壁模板印格为投影单元，通过对模型进行展开处理，得到塔筒外壁损伤展开布置图(见图10 所示)，损伤类型为混凝土破损与漏筋，网格为模板印格。可见，耐久性损伤主要出现在塔壁的下半部，损伤分布密集，损伤布置图将为塔筒耐久性处理的加固设计出图与现场施工提供重要依据。因此，采用多视角几何三维重建的数字图像检测方法可大大提升损伤检查的效率与准确度。类似应用场景还包括大规范工程结构施工过程质量、安全检测与监测[21]等。

图8 三维模型立面视图Fig. 8 Elevation view of 3D model

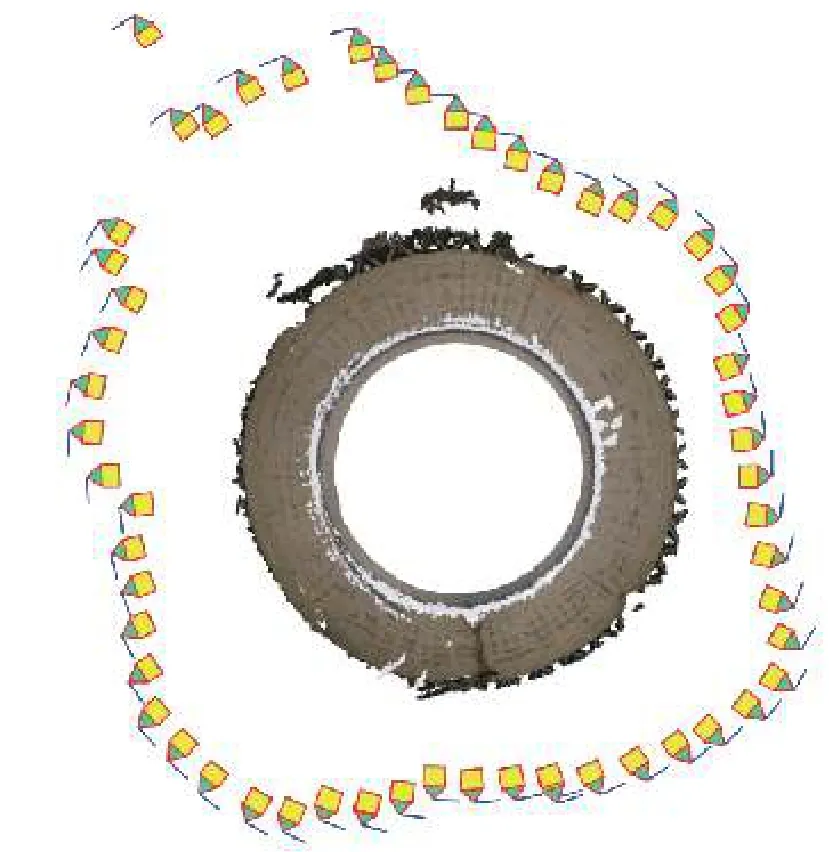
图9 三维模型俯视图Fig. 9 Top view of 3D model

图10 外壁损伤展开布置图(混凝土破损、漏筋)Fig. 10 Damage distribution of outer wall(concrete damage, rebar exposure)

5 应用研究③：钢结构构件变形识别

钢结构构件的几何变形在工程结构现场检查中较为常见，典型如网架的杆件弯曲、钢桁架角钢局部屈曲等。采用第2.2 节逆向工程建模与特征提取方法可准确识别空间几何变形损伤。以某体育场空间钢网格屋盖为例，采用多视角几何三维重建法对其中1 根弯曲变形杆件进行变形测量，图像拍摄使用佳能EOS 5D Mark III 相机，图像分辨率5760×3840，加密拍摄64 张不同视角下的图像，以此进行重建，形成的密集三维点云模型的局部放大图见图11 所示。图中，弯曲杆件清晰可见，点云分布均匀。在点云模型的基础上执行杆件轴心曲线拟合操作，提取准确的弯曲变形曲线，同时实现最大变形挠度的测量。图12 展示了提取的弯曲变形与使用全站仪测量的弯曲变形的结果比较，可见二者的误差相差不大，最大挠度的相对误差为5.05%，最大挠度所在杆件的轴向坐标的相对偏差为6.89%。事实上，通过观察图12中全站仪的变形测量曲线可以发现，全站仪测量的曲线并不光滑，与实际情况不符，原因在于圆形截面钢管沿轴向并无明显特征，全站仪沿轴向测量过程难以保持各测点均在截面中心，测得的变形曲线很可能是一条折线；相比之下，使用多视角几何三维重建法直接获取变形杆件的三维模型，在此基础上提取的轴心变形曲线则要准确的多。

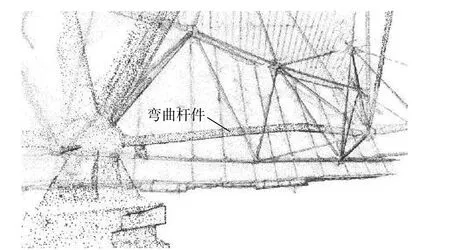
图11 变形杆件区域的三维重建密集点云模型Fig. 11 Three-dimensional reconstruction model of zone around deformed member

图12 钢管轴心变形测量对比Fig. 12 Comparison of axial deformation measurements of steel tubular member

6 结论

多视角几何三维重建法以运动恢复结构为核心算法，通过特征点识别、特征点匹配、相机运动参数估计、模型优化、稀疏点云三维重建等步骤，获得结构表面三维模型与摄影场景。结合二维数字图像处理与深度卷积神经网络等方法识别损伤，通过表面投影法解决成像几何变形与损伤定位，采用逆向工程建模与特征提取识别几何变形，可有效识别结构表面缺损与变形。方法具有以下应用优势：

(1)在精确定量检测中，可实现透射变形与复杂结构表面投影的几何变形的修正，获取准确的表面损伤分布、形状与其它参数；

(2)在大场景定量检测中，可在保持检测精度的同时，实现损伤定位，进一步生成损伤分布图；

(3)设备要求低、可方便快速地重建结构表面模型，重建形成的三维点云模型色彩真实丰富、点云精度较高，通过逆向工程建模与特征提取可实现几何变形检测。

多视角几何三维重建法在数字图像法工程结构检测、监测领域具有巨大的发展潜力与应用优势。结合无人机平台，可丰富摄影视角、极大提升数字图像获取能力，实现硬件平台与软件技术的互补结合。团队未来研究工作将围绕二者的结合开展结构损伤识别研究[22]。