内潮致拉格朗日余流的数值研究*
陈香伊,毛新燕,江文胜
(中国海洋大学 1.海洋与大气学院;2.海洋环境与生态教育部重点实验室,山东 青岛 266100)
内潮是发生在分层流体中的具有潮汐频率的波动,是内波的一种。当层化的海水在正压潮的驱动下流过剧烈变化的地形时,由于流动与地形的相互作用在海水中产生持续的周期性扰动,该扰动向外传播最终形成内潮[1-3]。对内潮的研究大多集中于其生成、传播、破碎、能量转化和混合等方面[4-6],但也有少数研究是针对内潮产生的非周期性流动即余流开展的,以此研究它所产生的物质输运。
在海洋中人们很早就注意到,从非线性波动中得到平均流动不是一个简单的事情。在水体及物质的净输运研究中,Longuet-Higgins[7]定义了非线性波动的物质输运速度,即对水微团追踪一个周期得到净位移后再除以周期,这是一种非常自然的处理方式,称为拉格朗日时均方法。但是在研究浅海潮致余流时,还有另一种滤掉周期信号的方法,即在定点处对一个周期内的潮流流速取平均[8],称为欧拉时均。用这两种时均方法得到的平均流动分别被称为拉格朗日余流和欧拉余流。Zimmerman[9]试图阐明潮致拉格朗日余流和欧拉余流之间的关系,而Feng[10]及其以后的系列研究不仅证明了在对流弱非线性下,物质输运速度是潮致拉格朗日余流的低阶近似,可以用欧拉余流与斯托克斯漂流速度的和表示,也证明了拉格朗日余流比欧拉余流更适合描述浅海环流及物质输运。但是由于欧拉余流在计算时的便利性,直至目前在浅海输运研究中仍有较普遍的应用。
在研究内波致余流时,也有类似的认识过程。Bretherton[11]研究内波导致的平均流时,使用的是欧拉时均。Grimshaw[12]则推导出内波致拉格朗日余流的控制方程组,并给出了斯托克斯漂流的计算方法,进而可以得到欧拉余流,但人们并不清楚这两者物理意义上的不同。其后,就像在潮致余流的研究中一样,这两个概念也是并行使用的。比如,Bordes等[13]通过水槽实验发现内重力波能造成强的水平余流,他们使用的就是对定点流速时间序列进行滤波的方法。Grisouard和Bühler[14]则在一个模型海域研究了内潮致拉格朗日余流的特征。Fan等[15]使用欧拉余流的概念研究了重力-惯性内波导致的平均流,并与实验室的结果进行了比较。
内潮余流是内波致余流在内潮情况下的一种特殊表现。Pindea[16]发现内潮涌可以引起物质输运;Maas和Zimmerman[17]发现内潮之间或内潮与正压潮之间的相互作用会产生余流,并给出小振幅地形下的余流结构;Chen和Beardsley[18]运用数值计算的方法将其拓展到了有限振幅条件下,也可以得到相似的余流结构;Lahaye等[19]在研究北大西洋洋中脊裂谷处深层流时发现内潮对平均流结构有着重要影响。
研究内潮余流有助于加深人们对内潮物质输运作用的理解,上述研究证明了内潮会导致余流的产生,且不同条件下的余流结构会有所不同。但使用不同的定义来研究内潮致余流,究竟会有何不同的结果,此前并没有人进行过对比研究,这是本文研究的主题。本文运用MITgcm数值模式,在包含单海脊地形的模式海域,计算了内潮致拉格朗日余流,与得到的欧拉余流进行比较,分析两者的差异,并给出不同地形、正压潮条件下的内潮致拉格朗日余流特征。
1 研究方法
1.1 内潮致拉格朗日余流及欧拉余流的定义
本文在计算内潮致余流时采用两种时均方式进行滤潮,分别得到了内潮致拉格朗日余流和欧拉余流。
拉格朗日余流uLR是指流体微团的流速在n个潮周期后的随体平均,即n个潮周期后流体微团的净位移除以所用的时间[9]:
(1)

欧拉余流uE是指定点处的瞬时流速在n个潮周期内的平均值[8]:
(2)
尽管欧拉余流在计算时有其便利性,但已有研究表明,拉格朗日余流在一阶近似下是物质输运速度[20],而欧拉余流则与物质输运速度之间则相差一个斯托克斯漂流速度[21]。因此本文将以拉格朗日余流为主要研究对象,同时也对拉格朗日余流与欧拉余流进行比较分析。
1.2 计算方法介绍
本文使用的模式是MIT General Circulation Model(MITgcm)[22],它是一个大气海洋通用模式,利用有限体积法求解流体力学方程,具有非静力近似计算的能力,因此可以模拟多种尺度的运动[23-25]。模式在底地形处采用“半网格”技术,能够准确刻画地形,适合用于内潮的模拟[26-28]。
在模式计算得到瞬时流场后,首先利用定点时均得到欧拉余流,其次利用轨迹追踪方法[29]计算拉格朗日余流,即追踪质点在运动n个潮周期后的净位移,然后除以运动时间nT。具体步骤如下:
水质点的轨迹方程为:

(3)
在Cartesian坐标系下,ξ=ξ(x,y,z)代表质点位移;u=u(x,y,z)=(u,v,w)代表质点的瞬时速度;t代表时间。
可以分别从x、y和z方向计算,下面以x方向为例追踪:
(4)
设某一网格中,东、西两侧面上的流速分别为uw、ue,则此网格中的某点流速u(x,y,z,t)通过线性插值得到:
u(x,y,z,t)=uw+x∂u/∂x。
(5)
(6)
将式(5)代入并化简得到
(7)
因此,水质点在经过一个时间步长Δt后的位移为Δx=x2-x1。若在时间Δt内水质点碰到网格的边界,则此追踪过程将分成多步完成:水质点在遇到网格边界时进入下一个网格,并在剩余时间Δtrest内在新网格内继续运动。设水质点运动到网格边界所用的时间为Δt1,则Δtrest=Δt-Δt1,Δx1为质点碰到网格边界之前的运动距离,则
(8)
如果运动再次碰到网格边界,则重复上面的步骤,直到Δtrest=0。
在计算拉格朗日余流时,取t0和t0+nT时刻的水质点位置数据,就可求得质点在运动n个潮周期后的净位移,进而计算出该方向的余流分量,其余方向的余流分量可采用相同的方法得到。
1.3 模式配置
模拟区域设置为二维x-z区域,选用Arakawa C网格,水平分辨率为500 m,垂向均匀分层,分辨率为10 m,网格数为600×450,水平尺度为300 km,最大水深为4 500 m。时间步长取为12 s,采用静力近似计算。科氏参量f=5.131 1×10-5rad/s,不考虑底摩擦。水平和垂向湍黏性系数分别为1和0.1 m2/s,取值与Legg和Huijts[30]相同,较大的湍黏性系数用于消除网格尺度噪音信号。取盐度为常数,仅让温度随深度线性变化,浮力频率为常数N=8×10-4rad/s。温盐扩散系数为0,确保在没有流动的情况下,背景层结稳定。
假设x轴为静止海面,z轴为西边界处,两者交点为坐标原点。海脊地形采用高斯分布:
其中:d(x)为x处的水深,H=4 500 m,为最大水深;h0表示海脊高度;L表示其宽度;x0=150 km,为海脊顶部的x坐标,即海脊在模拟区域的中间位置。东西两侧均为开边界。在东边界施加M2分潮流速强迫,频率为ωM2=1.405×10-4rad/s,振幅依据不同算例而设置,具体内容见下节。西边界采用海绵边界条件,宽度为40 km。模式在运行2天左右就可达到稳态,在计算第7天后开始追踪,追踪时间长度为一个M2潮周期,时间步长为216 s,得到拉格朗日余流,并在该时间段中进行定点时均得到欧拉余流。
1.4 算例设置
为分析内潮致余流随地形及外强迫变化的规律,在基准算例(Control run)之外,另设置了四组算例,分别为海脊宽度(Width)、高度(Hight)、正压潮流速(Velocity)和高度-正压潮流速组合(Hight3-Velocity),每组包含3个算例(见表1)。算例中各参数的选择参照邬丽丹[27]在研究南海内潮时统计得到的数据。Height3_Velocity组是在高窄海脊地形Height3算例的基础上将正压潮流速变大的一组算例,目的是观察较强非线性下余流结构的变化。


表1 算例参数设置Table 1 The configuration of parametersin different cases
2 结果
2.1 内潮结果
以基准算例为例验证内潮结果,图1(a)为区域中x= 100 km处的温度垂向分布时间序列,将1 700~2 000 m深度放大(见图1(b)),从模式启动到计算至第7天,可以看到计算2天后温度起伏稳定,振动幅度约为十几米,温度变化周期与M2分潮相同。图2为模拟第7天的水平斜压流速场,呈现出高模态内潮结构,存在波射线,从海脊附近激发产生向东、西两方向传播,遇到海面和海底时,波射线反射。斜压流场是潮流去掉垂向平均的正压潮后得到的,其量值相对较小,平均值为1.02 cm/s,最大值为2.61 cm/s,集中于波射线处。由于强迫施加于东边界处,正压潮自东向西流经变化的地形时,在海脊东侧为爬坡过程,海脊西侧为下坡过程,下坡时深度逐渐加深,产生的内潮更强,因此海脊两侧内潮强度有所不同。

图1 基准算例温度垂向分布时间序列Fig.1 Time series of temperature profile for the control run

图2 基准算例瞬时水平斜压流速分布(第7天)Fig.2 Distributionof horizontal component of baroclinic velocityin the 7th day from the control run
2.2 内潮致拉格朗日余流
内潮致拉格朗日余流结果如图3(a)所示,拉格朗日余流与内潮结构(见图2)相对应,主要沿波射线分布。余流从海脊顶部附近产生向东、西两个方向流动,余流的水平分量平均值为2.97× 10-3cm/s,垂向分量平均值为3.08× 10-4cm/s,余流以水平分量为主。考虑到垂向分量在内潮运动中的重要性,本文将垂向分量同地形水深一起扩大了30倍,故图3(a)所示流场体现沿波射线运动的特征。对于余流量值而言,可发现波射线位置处的余流较大,远离波射线的区域余流值很小。Lamb[33]在讨论内波引起的物质输运时曾指出输运与海洋分层和垂向位置有关,上述内潮致余流的沿波射线分布也会产生类似的输运效果。
此外,在海脊附近余流量值的波射线结构十分清晰,开边界附近余流减弱,且水平分量在垂向上发生多次东西转向。
为患者提供显微手术的时候,应该要对患者的脑组织进行保护,使用电凝的功率要尽量小,防止患者的周围神经组织被灼伤。并且对瘤体切割的时候,要进行止血操作,使用冲水的方式来进行降温,降低脑组织附近受到的影响,避免对患者的生活带来影响。
内潮致拉格朗日余流与斜压流相比,平均值之比为0.003,但是余流最大值为2.76× 10-2cm/s,比平均值大一个量级,其与最大斜压流的比值为0.011,在实际海洋中,以南海为例,若斜压流速为0.1 m/s的量级[34],则余流较大处可达1 mm/s,一个周期内质点的净位移也有十几至几十米,对于物质输运的作用不可小觑。

(背景颜色代表余流的水平分量,红色箭头表示余流的方向。The background color represents the horizontal component of the residual velocity;The red arrow indicates the direction.)图3 拉格朗日余流场Fig.3 Lagarangian residual velocity (LRV) field
计算相同条件下的正压潮致拉格朗日余流(见图3(b)),发现除了在海脊附近的一些流动外,整场的拉格朗日余流非常小,内潮致拉格朗日余流与正压潮致余流水平分量的平均值之比为23.70,因此模拟所得拉格朗日余流确实是由内潮非线性效应产生的。殷鹏等[35]在正压潮和内潮情况下分别进行了粒子追踪,也发现内潮会引起更强的输运效应。
3 讨论
3.1 两种内潮致余流的对比
内潮致欧拉余流结果如图4所示,也以水平流动为主,余流较大值出现在海脊附近和海面与海底层波射线的位置,其平均值为2.43× 10-3cm/s,最大值为5.75× 10-2cm/s,与拉格朗日余流量值相当。两种余流的最大区别在于海脊附近的流动方向相反,欧拉余流为向海脊辐聚,而拉格朗日余流为辐散。Lucas等[36]的研究表明,南加州湾陆架海域初级生产力的提高与内潮驱动的营养物质自深海向岸的水平输运有关,Moore和Lien[37]发现鲸群会随着内波传播的方向游动以寻找食物,这都表现出了内潮导致的从生成区向岸输运的特性。模拟所得内潮致拉格朗日余流自海脊附近向两侧辐散的特征,有利于营养物质的向岸输运。
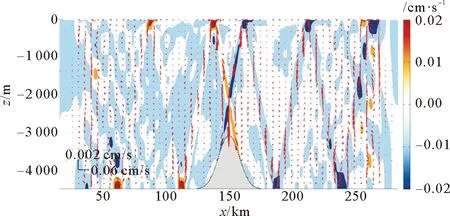
图4 同图3(a),内潮致欧拉余流分布Fig.4 Same as Fig.3(a),but the Eulerian residual velocity induced by internal tide
Feng[10]通过推导得到拉格朗日余流满足物质面守恒这一结论,并且可以将物质面看作流场中的任一守恒量的等值面。内潮发生时流体内部有密度分层,等密面(本文中则为等温面)可被视为一种物质面。在拉格朗日余流的定义下,任取一水质点,其在一个周期内的温度随时间变化很小(见图5),可理解为在拉格朗日余流计算中,追踪的水质点不离开物质面,即内潮致拉格朗日余流满足物质面守恒原理。而以欧拉余流的定义,即固定点的温度,则呈现出很强的周期性变化,显然通过该空间点的水质点不在一个等温面上,即在一个周期内不能保证在同一个物质面上,因此欧拉余流不满足物质面守恒。

图5 初始位置x=145 km,z=-1 150 m的水质点温度的随体时间变化(蓝线)和定点时间变化(红线)Fig.5 Time series of temperaturealong with the water parcelof initial position x=145 km,z=-1 150 m (blue lines) and at the fixed point of the same position(red lines)
3.2 不同条件下内潮致拉格朗日余流的特征
下文将利用几组敏感性实验,讨论地形及正压潮流速对余流结构的影响。
3.2.1 海脊宽度对内潮余流的影响 当海脊高度和正压潮流速不变,宽度逐渐增加时(算例Width1~Width3),ε变小,导致内潮结构由高模态向低模态转变(见图6):波射线消失,变为流速上下反向的第一模态结构,斜压流速也逐渐变小。这些变化与邬丽丹[27]所得结论相同,且下文中内潮结构随各参数的变化均与前人一致。图7为相应的拉格朗日余流结果,同样地,随着海脊宽度增加,射线结构消失,余流结构混乱,余流值逐渐减小。海脊顶附近余流明显减弱,而开边界附近的余流较强,水平分量在垂向上发生多次转向。可见,余流沿波射线分布的结构特征主要与高模态内潮有关。

图6 随海脊宽度变化的斜压流水平分量场Fig.6 Horizontal component of baroclinic velocity field
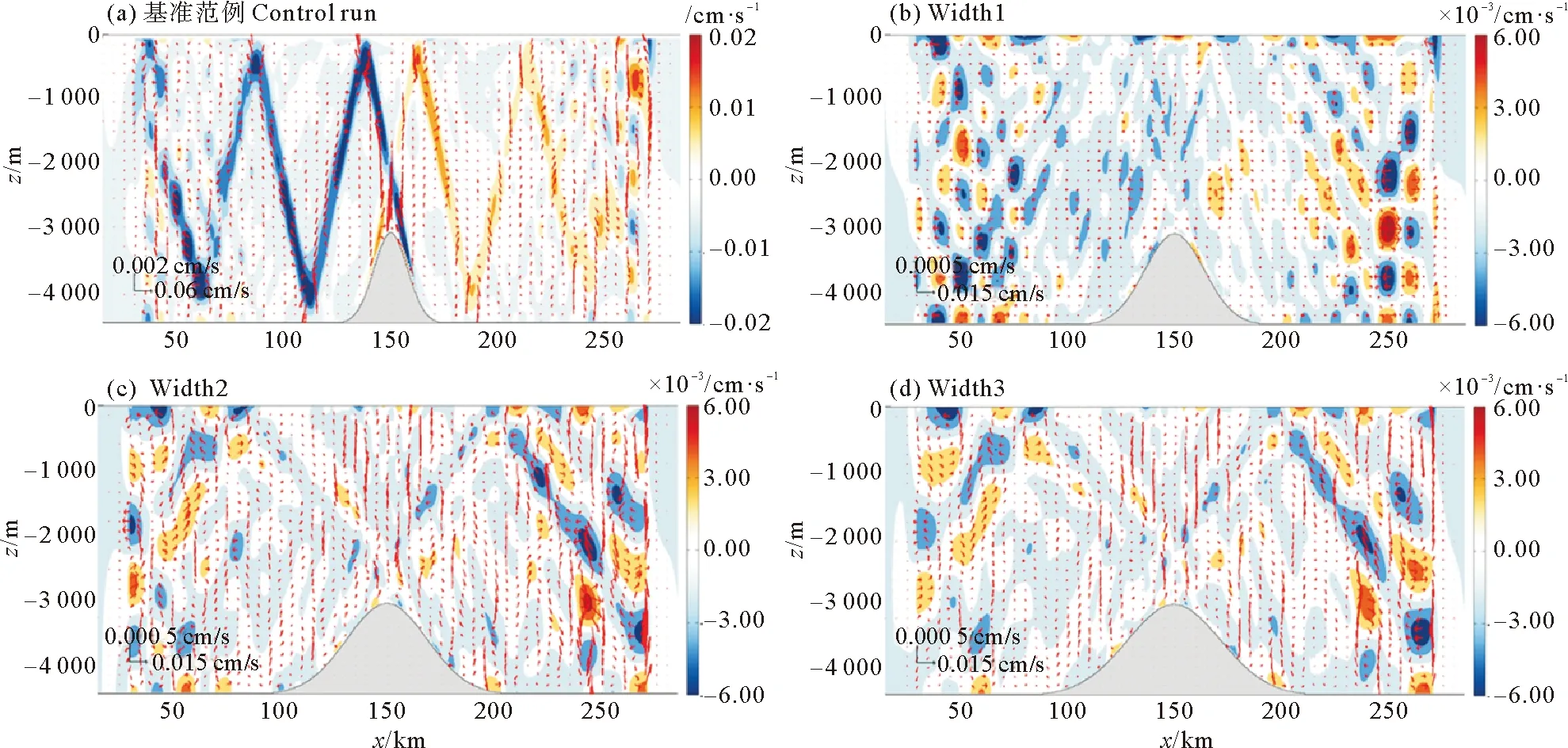
(背景颜色代表余流的水平分量,红色箭头表示余流的方向。The background color represents the horizontal component and the red arrow indicates the direction.)图7 同图6,内潮致拉格朗日余流Fig.7 Same as Fig.6,but the LRV induced by internal tide
3.2.2 海脊高度 当海脊高度逐渐增加时(算例Height1-Height3),内潮结果变化不大,保持为波射线结构(图略)。拉格朗日余流流速逐渐变大,依然有从海脊顶部附近向东、西两方向的流动(见图8)。由于波射线斜率s仅与内潮频率ω和分层强弱N有关,因此当地形高度变高时,波射线角度不变。但在海脊附近产生的余流逐渐变为向四个方向的流动(Height3),除了向海面方向的两支流动外,还产生向海底方向紧贴着海脊斜坡的流动,这可能是由于海脊高度变高使得向海底方向的流动有了发展空间,最终在海脊附近可见两支平行的余流射线。余流在海脊附近的流动较强,在向东、西两侧流动过程中,余流减弱变快,因此只在海脊附近可见清晰的沿波射线分布特征。
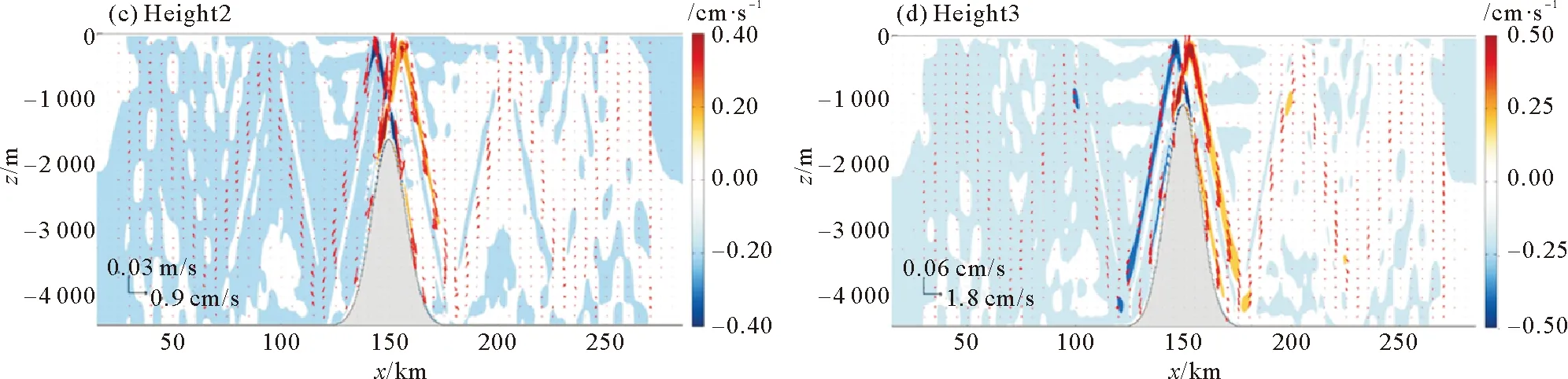
图8 同图7,随海脊高度变化的内潮致拉格朗日余流Fig.8 Same as Fig.7.but the LRV induced by internal tide with variation of ridge height
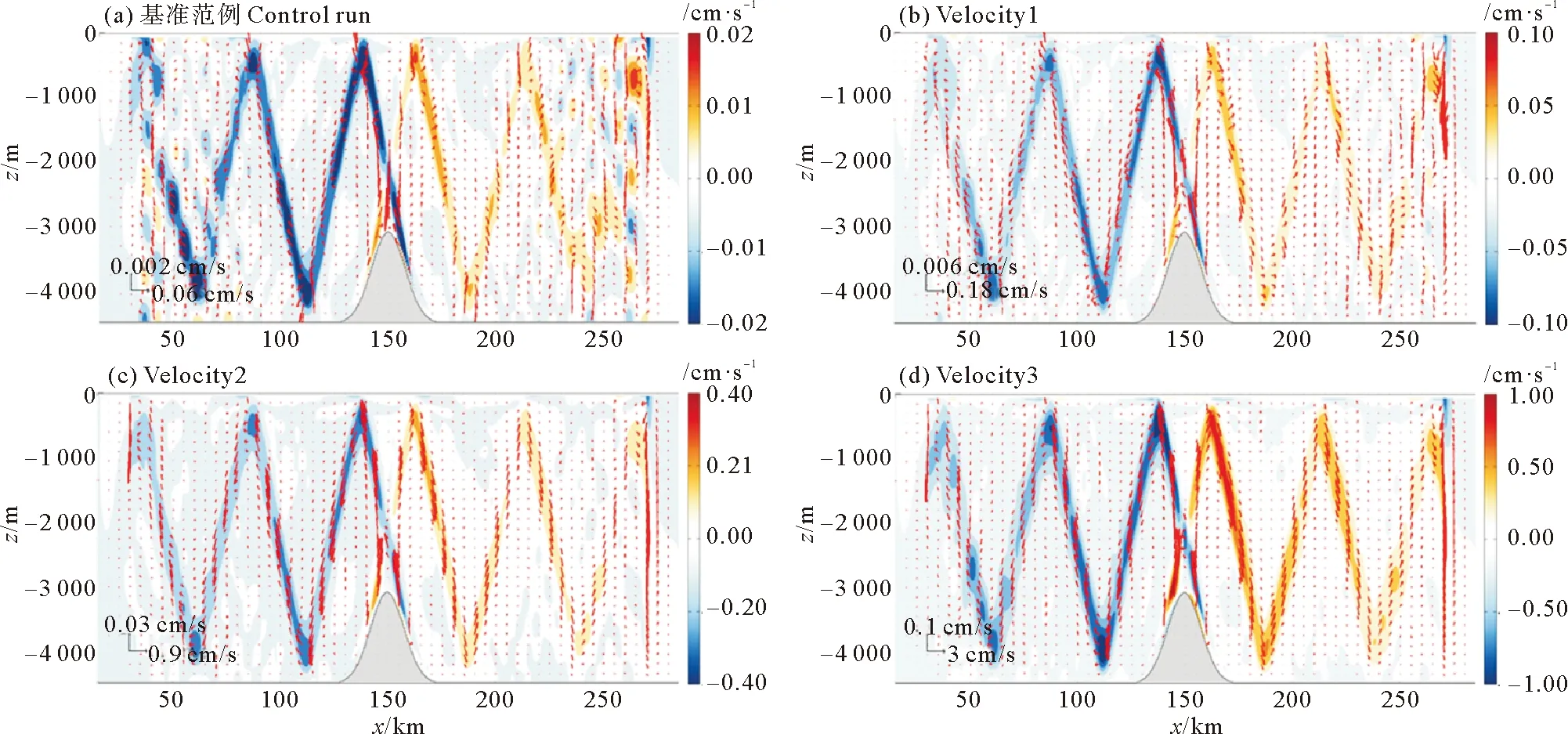
图9 同图7,随正压潮流速变化的内潮致拉格朗日余流Fig.9 Same as Fig.7.but the LRV induced by internal tide with variation of barotropic velocity
在高窄地形-正压潮流算例(Height3-velocity)中,观察正压潮流速变化的影响,发现正压潮流速变大会使非线性效应加强,α增大,波射线结构出现混乱(见图10)。但从余流结果(见图11)上来看,余流依然保持原有的特征,即海脊附近余流沿波射线分布明显,在向外流动过程中余流减弱。海脊附近平行的余流射线间的距离随着正压潮流速的增加而减小,最终合为一支从海脊顶部产生的流动(Height3_Velocity3)。
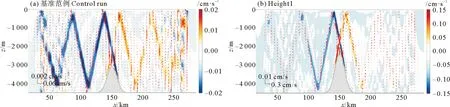

(背景颜色代表余流的水平分量,红色箭头表示余流的方向。The background color represents the horizontal component and the red arrow indicates the direction.)图11 同图10,内潮致拉格朗日余流Fig.11 Same as Fig.10,but the LRV induced by internal tide
4 结语
本文利用MITgcm模式,计算单海脊地形下的内潮致拉格朗日余流和欧拉余流,比较二者之间的差异,并讨论了地形、正压潮流速等参数对余流结构的影响。
内潮致拉格朗日余流与内潮结构相对应,主要沿内潮波射线分布。余流从海脊附近,向东、西两方向流动,余流较大值集中于波射线位置处。正压潮致拉格朗日余流比内潮致余流小至少1个量级,证明了余流是由内潮作用产生的。
与欧拉余流相比,拉格朗日余流在海脊附近呈现辐散的特征,而欧拉余流表现为辐聚特征。拉格朗日余流的辐散特性可以更好的解释内潮引起的物质向岸输运,并且拉格朗日余流可以证明其满足物质面守恒条件。
地形、正压潮流速等参数的改变会引起拉格朗日余流结构的变化。当海脊变宽时,余流随内潮波射线结构的消失而变得很小且混乱;当海脊变高时,海脊附近逐渐产生向海底方向的流动,与海面反射的余流形成平行的射线,余流整体增强,海脊附近的余流在向外流动过程中增幅减小;当正压潮流速增大时,余流结构基本不变,但在高窄海脊地形下海脊附近的平行射线会逐渐合为一支从海脊顶部产生的流动。
总之,内潮致拉格朗日余流结构呈现明显的规律性,且与内潮流速结构有很好的对应关系,因此内潮致物质净输运,对于海洋内部的水文、生态要素等分布会产生一定的影响。本文研究只是一个初步探讨,对于内潮致物质输运作用在实际海洋中的应用仍需更多深入的研究。

