MIMO多向中继信道在完整数据交换模型下的自由度*
李勇,袁晓军
(1 中国科学院上海微系统与信息技术研究所, 上海 200050; 2 上海科技大学信息学院,上海 201210;3 中国科学院大学,北京 101408; 4 电子科技大学通信抗干扰技术国家级重点实验室,成都 611731)
多向中继信道模型(multiway relay channel, mRC)[1-2]主要有以下两种数据交换模型:成对的数据交换模型,即两个用户相互交换信息;完整的数据交换模型,即一个用户将相同的信息广播给多个用户。此模型在实际应用中普遍存在。例如,社交网络中,多个小组的用户希望在同组中共享文件。由于网络中每个节点配置有多根天线,多输入多输出(multiple input multiple output, MIMO)mRC可以极大地提高复用增益。但是由于中继信道的信道容量难以刻画[3],所以很多工作集中在模型自由度(degree of freedom, DoF)的分析上,即高信噪比下的性能特点。简单说,网络的DoF是网络中可以支持的独立数据流数目[4]。
目前,国内外学者对于mRC的DoF分析已经有了一些结果,但是大多数研究集中在成对的数据交换模型[5-9]中,尤其是基于成对数据交换模型的一种特殊模型,Y-信道模型[10-11]。并且由于成对数据交换模型上行和下行链路是对称的,所以大多数工作集中在全双工通信模型。相比来说,对于完整数据交换模型的分析相对较少,并且由于完整数据交换模型上行和下行链路是非对称的,分析半双工通信下系统可达的DoF也非常重要。文献[12]给出全双工通信下有多个用户集群的完整数据交换模型一个可达的DoF。对于有多个用户集群,每个用户集群中有多个用户的信道模型,通过设计信号对齐,给出此模型一个一般化的结果。文献[13]分析半双工通信下有一个用户集群,用户集群中有多个用户的完整数据交换模型的DoF。此模型中,对于每一个用户来说,没有来自于其他用户集群的干扰信号。作者推出此模型在半双工通信下的DoF容量,即验证了此模型的割集上界是可达的。并且当上行和下行时隙相等时,作者将半双工通信的结果推广到全双工通信。由于有多个用户集群的完整数据交换模型比较复杂,直接分析其DoF比较困难,文献[14]结合优化算法[15]推出一个优化的结果。但是此算法仅对全双工通信有效,对于半双工通信下的DoF仍然未知。
本文研究半双工通信下两个用户集群,每个用户集群中多个用户的MIMO mRC在完整数据交换模型下可达的DoF。同时对于全双工通信,假设每个结点可以进行自干扰消除。所以当上行和下行时隙相等时,半双工通信的结果可以推广到全双工通信,即此时全双工通信的结果是半双工通信的2倍。将半双工通信下上行和下行时隙相等的结果推广到全双工通信,并且验证该信号对齐方案可以达到全双工通信目前最优的结果。
1 系统模型
1.1 信道模型
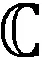
图1 两个用户集群,每个集群中K个用户的MIMO mRC 模型 Fig. 1 The MIMO mRC with two clusters each of which contains K users
考虑物理层网络编码[16],整个数据交换包含两个传输链路,即上行链路和下行链路。上行链路所有用户将信号发送给中继,下行链路中继将信号广播给所有用户。假设上行和下行链路分别包含Tu和Td个时隙,则在第t个时隙,信道模型可以表示为
(1)
(2)
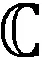
由于上行和下行链路分别包含Tu和Td个时隙,上述信道模型简化为
(3)
(4)
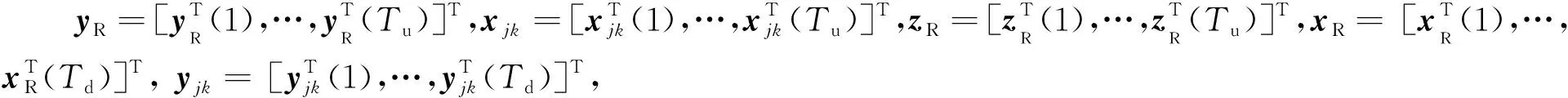
Hjk=diag{Hjk(1),…,Hjk(Tu)}
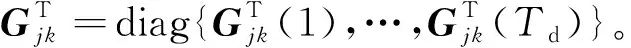
1.2 用户端和中继端的预处理
假设用户Γjk发送信号Wjk给同一集群j中其他所有用户,并且希望收到来自集群j中其他所有用户发送的信号Wjk′,其中k′∈IK
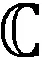
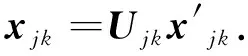
(5)
接下来考虑中继端的处理。为了描述方便,引入以下符号:
Mj=[Hj1Uj1,…,HjKUjK],j∈IL,
(6a)
(6b)
M=[M1,M2],
(6c)
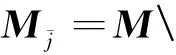
(6d)
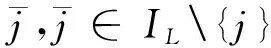
PjyR=PjMjx′j+PjzR,
(7)
其中x′j=[x′j1,…,x′jK]T。式中,通过投影,集群j′≠j中的信号被去除了。
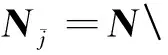
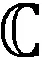
因此,中继端发送的信号为
(8)
式中:α为中继端满足功率限制的缩放因子。
最终,用户Γjk收到的信号为
(9a)
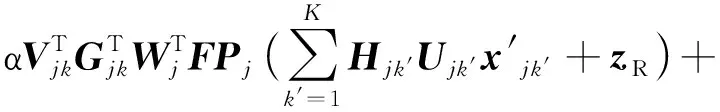
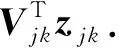
(9b)
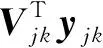
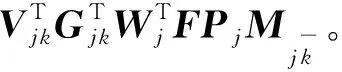
1.3 自由度
由于MIMO mRC的香农容量很难刻画,因此本文主要分析网络的DoF。简单来说,网络的DoF是网络中可以支持的独立信息流数目。
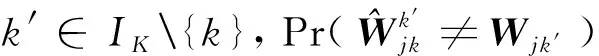
(10)
式中:Cjk(P)单位是bit,log表示对数以2为底,同时,定义每个用户可达到的DoF为
(11)
式中:duser表示用户收到的独立的数据流数目。
注意:考虑全双工通信时,此信道模型的一个割集上界[12]为dsum≤min(KLM,KN),即平均每个用户收到的DoF为
(12)
2 问题讨论
2.1 初期讨论
分别对上行和下行链路进行分析。
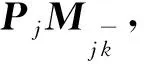
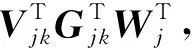
结合以上对上行和下行链路的分析,如果设计上行预处理矩阵Ujk和下行接收处理矩阵Vjk满足
rank(PjMj)≥(K-1)duTu,
(13a)
(13b)
则用户Γjk的自由度取决于上行链路集群j中其他所有用户发送的数据流数目(K-1)duTu和下行链路它能接收到的数据流数目ddTd,即每个用户可达的DoF为
(13c)
为描述方便,后文分别称du和dd为上行和下行链路每个用户可达的DoF。
由于我们的信号对齐方案不考虑多个时隙之间的信号对齐,所以接下来考虑单个时隙下(此时Tu=Td=1)如何设计信号对齐,使得du和dd最大。
2.2 相关引理和定义
对上行和下行链路设计信号对齐时,均使用了天线禁用技术和角点的概念[12]。接下来以上行链路为例对天线禁用技术进行介绍,并且对角点进行定义。
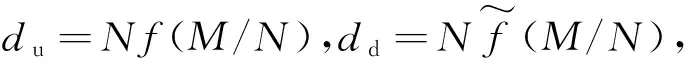
引理1(天线禁用技术)对于所考虑的MIMO mRC,假设上行链路du=Nf(M/N)在一个固定的天线配置 (M=M0,N=N0)时,du=d0可达。那么通过在用户端禁用M-M0根天线,(x=M/N0,y=du)在线段x∈[M0/N0,∞),y=d0上的每个点可达;通过在中继端禁用N0-(MN0/M0)根天线,(x=M/N0,y=du)在线段x∈(0,M0/N0],y=(d0N0/M0)x上的每个点可达。
通过天线禁用技术,只需要给出可达DoF曲线中特定的点,即可得到整个可达DoF曲线。接下来,称这些特定点为角点,并给出以下定义。
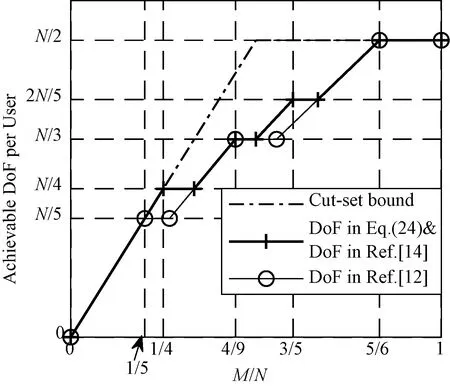
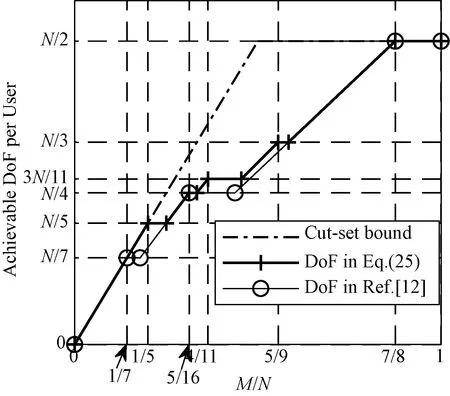
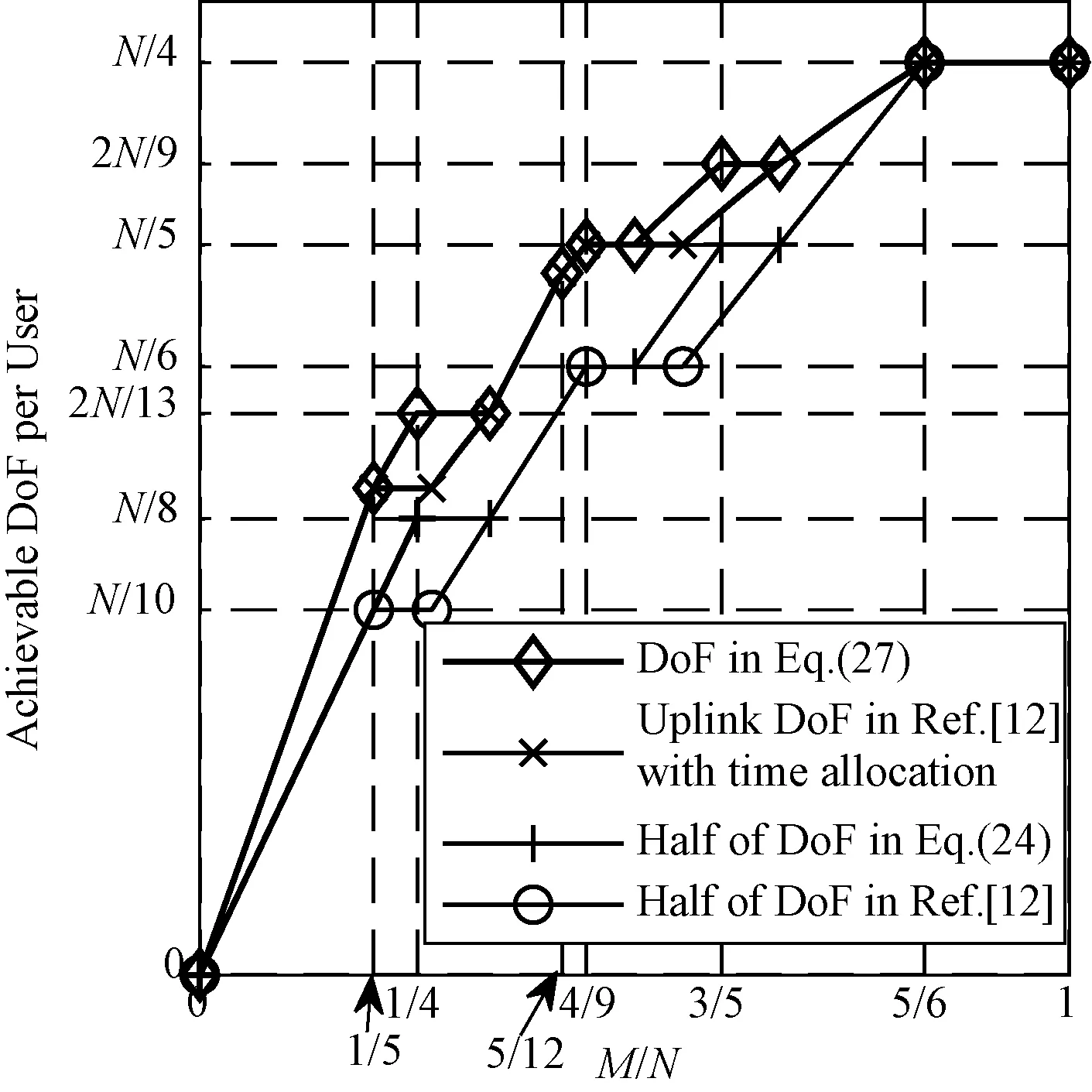
定义1(角点)已知上行链路一个可达的DoF曲线du=Nf(M/N),固定中继端天线N=N0。对于可达DoF曲线中某一点(M0/N0,d0), 如果当M>M0时,(M/M0,d0M/M0)不可达;并且当M 以上对天线禁用技术的描述和角点的定义同样适用于下行链路。接下来,只需找到上行和下行链路所有的角点,并且结合天线禁用技术,即可得上行和下行链路的可达DoF,即du和dd。为描述方便,定义g函数 (14) 式中a和b是常系数。 上行链路设计信号对齐满足单个时隙下rank(PjMj)≥(K-1)du。接下来,给出候选角点(M/N,du),并结合候选角点给出相应的可达DoF。 引理2对于两个用户集群,每个集群K个用户的M×NMIMO mRC,当数据交换模型为完整数据交换模型时,对于上行链路以下候选角点(M/N,du)是可达的: (15a) (15b) 定义集合I包含式(15)中所有候选角点(M/N,du),则上行链路每个用户可达的一个DoF为 (16) 证明已知候选角点,根据天线禁用技术,可以得到式(16)。接下来设计信号对齐证明角点(U1)和(U2)满足rank(PjMj)≥(K-1)du。 (17) (18) 引理3 对于两个用户集群,每个集群K个用户的M×NMIMO mRC,当数据交换模型为完整数据交换模型时,下行链路以下候选角点(M/N,dd)是可达的: (19a) (19b) (19c) 定义集合J包含(19)中所有候选角点(M/N,dd),则下行链路每个用户可达的一个DoF为 (20) 证明已知候选角点,根据天线禁用技术,可以得到式(20)。接下来我们设计信号对齐证明角点(D1), (D2)和(D3)满足rank(WjGjkVjk)≥dd。 (21) (22) 因此,span(Gj1Vj1,…,GjKVjK)=span(Gj1Vj1,…,GjkVjk),并且以概率1是kN/(k+1)维度。此时,每个用户接收dd=N/(k+1)个独立数据流,经过信号对齐,在中继端一个集群接收的KN/(k+1)个数据流压缩到kN/(k+1)个空间维度。所以中继端发送给另一个集群的无干扰信号维度为N-kN/(k+1)=dd。即rank(WjGjkVjk)=N-kN/(k+1)=dd。 证毕。 引理2和引理3分别给出两个用户集群,每个集群K个用户的MIMO mRC完整数据交换模型上行链路的候选角点(M/N,du)∈I和下行链路的候选角点(M/N,dd)∈J。并根据候选角点给出相应的可达DoF。 接下来,结合引理2和引理3,给出此模型一个可达的DoF。 考虑全双工通信,假设每个结点都可以进行自干扰消除,则以上对半双工通信的分析经过调整可以应用于全双工通信。全双工通信和半双工通信主要的区别在于,对于全双工通信,每个结点同时发送和接收信号,因此上行和下行链路总是占用相同的时隙,即Tu=Td=T。由于引理2和引理3均考虑单个时隙下的信号对齐,由此,令Tu=Td=T,很容易推出此模型全双工通信下一个可达的DoF。 定理1对于两个用户集群,每个集群K个用户的M×NMIMO mRC,当考虑完整数据交换模型,并且考虑全双工通信时,每个用户可达到的一个DoF为 (23) 令定理1中K=3和K=4,给出以下结论。 推论1对于L=2,K=3的M×NMIMO mRC,当考虑完整数据交换模型,并且考虑全双工通信时,每个用户可达的一个DoF为 (24) 证明当K=3时,下行链路存在以下候选角点(M/N,dd): 由式(23)得到推论1。 推论2对于L=2,K=4的M×NMIMO mRC,当考虑完整数据交换模型,并且考虑全双工通信时,每个用户可达的一个DoF为 (25) 证明当K=4时,下行链路存在以下候选角点(M/N,dd): 由式(22)得到推论2。 图2和图3分别给出L=2,K=3和L=2,K=4全双工通信下系统可达到的DoF。对于L=2,K=3,将全双工通信下的割集上界以及文献[12],[14]的结果加入进去比较。由于得到2个更优的角点(1/4,N/4)和(3/5,2N/5),我们的结果在这2个角点附近优于文献[12]中的结果。同时,此结果和文献[14]使用算法优化得到的结果相同。而且这也是目前为止此模型最优的可达DoF。对于L=2,K=4将全双工通信下的割集上界以及文献[12]的结果加入进去比较。此时,得到3个更优的角点(1/5,N/5),(4/11,3N/11)和(5/9,N/3),所以在这几个角点附近我们的结果优于文献[12]中的结果。 图2 全双工通信L=2,K=3模型可达到的DoFFig. 2 Achievable DoF of MIMO mRC with L=2 and K=3 in full duplex model 图3 全双工通信L=2,K=4模型可达到的DoFFig. 3 Achievable DoF of MIMO mRC with L=2 and K=4 in full duplex model 注意:考虑全双工通信时,由于网络的瓶颈是下行链路,所以文献[12]中作者考虑上行和下行链路对称设计是足够的,同时,作者假设每个用户发送一个独立的数据流,则将一个集群的信号尽可能压缩到一维。这和我们下行链路设计信号对齐的要求(13b)是类似的。但是我们在设计下行链路信号对齐时考虑了更多的信号对齐模式,所以得到了更优化的结果。 通过定理1进一步验证了对于完整数据交换模型,下行链路是网络的瓶颈。所以对于半双工通信,通过优化上行和下行链路的时隙可以使系统的DoF进一步提高。 定理2对于两个用户集群,每个集群K个用户的M×NMIMO mRC,当考虑完整数据交换模型,并且考虑半双工通信时,优化上行和下行链路的时隙分配为 (26a) 此时每个用户可达的一个DoF为 (26b) 其中,集合I和集合J分别包含式(15)和式(19)中的角点,g函数定义在式(14)中。 令定理2中K=3,得到以下结果。 推论3对于L=2,K=3的M×NMIMO mRC,当考虑完整数据交换模型,并且考虑半双工通信时,优化上行/下行链路的时隙分配为 (27a) 此时每个用户可达的一个DoF为 (27b) 证明当K=3时,上行链路存在以下候选角点(M/N,du): (28) 结合推论1下行链路可达的DoF以及定理2,得到推论3。证毕。 注意:根据2.1节的讨论,当上行链路设计信号对齐满足rank(PjMj)≥(K-1)duTu。下行链路采用文献[12]的结果,通过优化上行和下行链路的时隙分配,可以得到L≥2 个用户集群,每个用户集群中K≥3个用户的MIMO mRC模型在半双工通信下可达的一个DoF。但是由于文献[12]中下行链路设计信号对齐的方式并不是最优的,所以最终得到的半双工通信下的结果并非最优。 图4给出半双工通信下L=2,K=3模型可达到的DoF。对于半双工通信,当不考虑上行和下行链路时隙优化分配时,系统可达的DoF是全双工通信的一半,很容易得到半双工通信下两个可达的DoF,即定理1中duser的1/2 以及文献[12]结果的1/2。在图4中将此不考虑时隙分配的结果加入进行比较。同时,如前所述,结合2.1节的讨论,文献[12]的结果经过上行和下行时隙优化分配,很容易推广到半双工通信。对于L=2,K=3,当上行链路设计信号对齐得到式(28),下行链路采用文献[12]中的信号对齐方式时,可以推出半双工通信下经过上行/下行时隙优化后一个可达的DoF。将此结果加入图4进行比较。结果发现当M/N<5/6时,进行时隙优化分配后的结果明显优于不进行时隙分配的结果。同时,由于下行链路考虑了2个更优的角点(1/4,N/4)和(3/5,2N/5),在这2个角点附近可得到更优化的DoF。 图4 半双工通信L=2,K=3模型可达到的DoFFig. 4 Achievable DoF of MIMO mRC with L=2 and K=3 in half duplex model 注意:半双工通信时,上行和下行链路信号对齐非对称设计使得系统DoF进一步提高。这是因为对于一次完整的数据交换,上行链路中继端需要解出一个集群所有用户发送的信号,对应于式(13a),下行链路中继端为每个集群中的所有用户发送相同的信号,对应于式(13b)。很明显,上行链路的信号对齐要求相比下行链路降低了,这是因为如果上行链路一个集群的信息在中继端压缩得过于严重时,需要消耗多余的时隙将压缩的信息解出来。 由于L个用户集群,每个集群K个用户的MIMO mRC的完整数据交换模型较为复杂,目前此模型全双工通信和半双工通信下的信道容量是未知的。本文主要对两个集群,每个集群K个用户的MIMO mRC的完整数据交换模型进行分析。由于数据交换模型的特殊性,上行和下行链路的信号对齐是不对称的,所以对上行链路和下行链路分别设计信号对齐,得到相应的角点,并根据角点给出每个用户上行链路可以发送的独立数据流数目du和下行链路可以接收的独立数据流数目dd。对于全双工通信,假设每个结点可以进行自干扰消除,通过令Tu=Td=T,推出此模型在全双工通信下的结果。同时,由于下行链路是网络的瓶颈,通过上行和下行链路非对称设计,并且优化上行/下行链路时隙分配,得到半双工通信下一个优化的DoF。 通过给出全双工通信下L=2,K=3和L=2,K=4的可达DoF,验证了我们的结果优于目前已知的结果[12],并和通过算法优化得到的结果[14]相同。同时通过优化上行/下行链路时隙分配Tu/Td,半双工通信下的L=2,K=3系统的DoF进一步得到提高。本文分析对于更一般的完整数据交换模型(L>2)在全双工通信和半双工通信下的DoF分析有参考价值。3 信号对齐
3.1 上行链路信号对齐
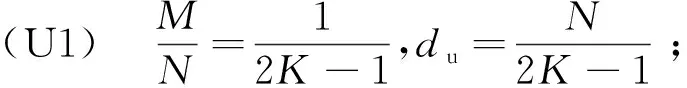
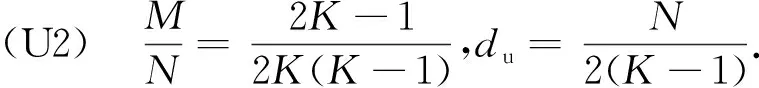
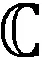
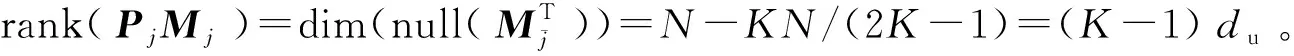
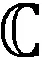
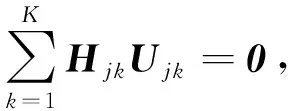
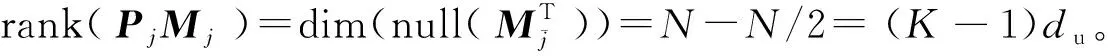
3.2 下行链路信号对齐
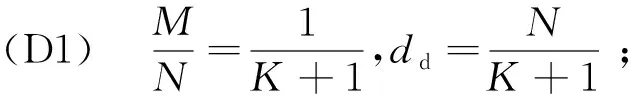
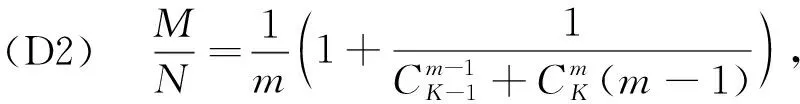
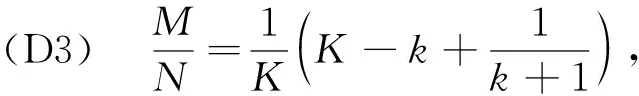
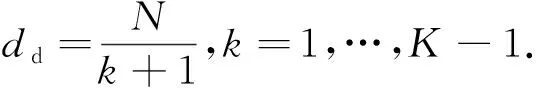
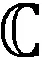
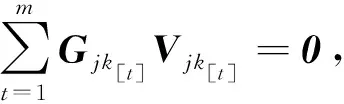
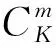
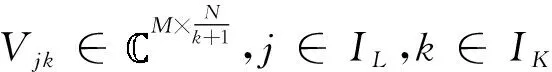
4 主要结果
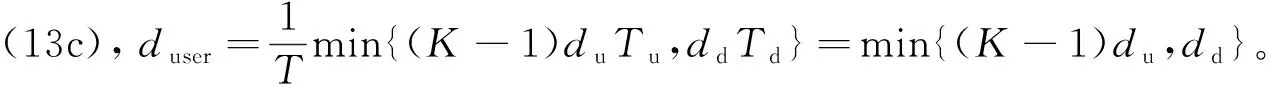
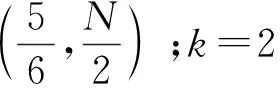
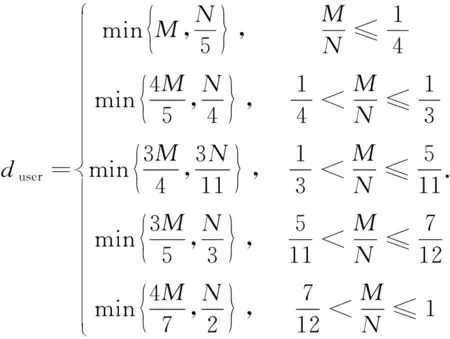
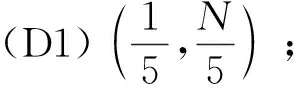
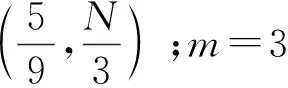
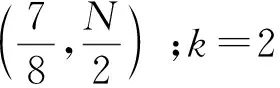
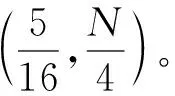
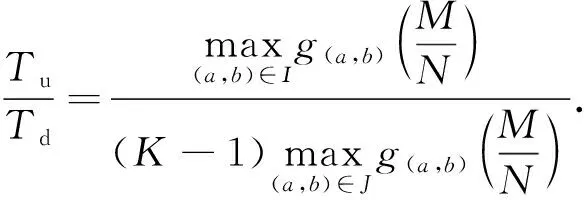
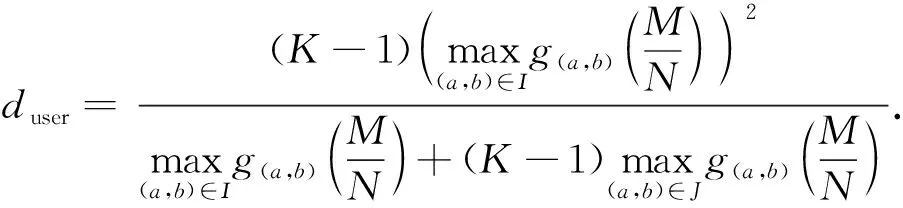
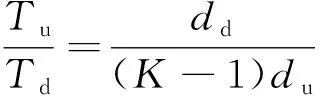
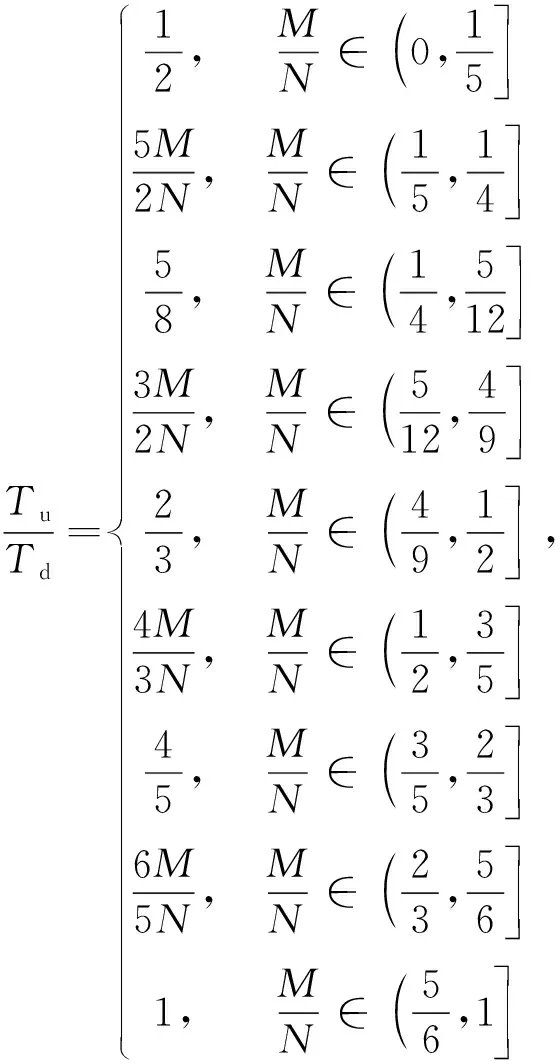
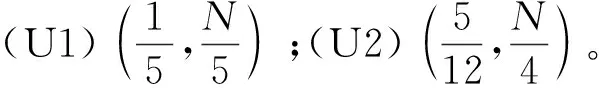
5 总结

