股票市场和公司债市场风险溢出效应

王鹏飞

（中国社会科学院数量经济与技术经济研究所，北京 101118）

一、引言

在经济下行压力加大、杠杆攀升和外部环境复杂严峻等背景下，虽然短期内不会出现大的金融危机，但金融风险具有隐蔽性和复杂性，系统性金融风险呈现不断积累的趋势。股票市场和公司债市场作为系统性金融风险的重要研究对象一直备受关注。近年来股票市场的价格波动异常剧烈，极端的涨跌停现象增加了投资者的风险。此外，2015 年1 月证监会发布了《公司债券发行与交易管理办法》，为公司债的发展提供了法律支持。根据《2018 年公司债市场发展报告》，2018 年交易所债券市场共有969 家发行人共计发行各类公司债11829 期，发行规模合计22469.08 亿元，但公司债市场违约金额高达407.45 亿元，调降事件达到52 次，其中以民营企业占比较高。股票和公司债券作为公司融资的重要渠道，其价格的变化波动依赖于公司的发展状况，股票市场和公司债市场之间存在一定的风险相依和风险传染效应。

金融市场中的风险溢出效应测度方法主要有CoVaR、MES、SRISK、CCA 和Network 等。其中，CoVaR 模型是目前风险溢出效应测度的主流度量方法，Adrian and Brunnermeier(2016)对CoVaR 模型进行了系统的介绍，CoVaR 指标描述了单个主体处于危机条件下的金融体系的条件风险水平，而ΔCoVaR 指标则反映了单个金融机构的风险外溢至其他金融机构或者整个金融市场。Girardi and Ergün(2013)对CoVaR 模型的条件风险进行了拓展和改进，即由分位点下的收益率等于VaR 推广至最多等于VaR，以此来更为全面反映尾部风险的信息。另外，Cao(2013)提出了多条件CoVaR 模型，研究多个金融机构同时陷入危机时对金融系统的风险溢出问题，考虑了多个金融机构的危机条件，而不是单个金融机构。

目前对CoVaR 模型的估计方法主要有分位数回归、GARCH和Copula 等。分位数回归常用于描述金融机构之间线性的风险相关关系，张瑞、刘立新(2018)通过极端分位数回归方法，构建非对称CoVaR 模型，准确反映了上市银行与金融系统尾部风险的联动性。White(2015)将分位数回归扩展至多元分位数回归，从单个金融机构的系统性风险推广至多个金融机构的系统性风险，可以刻画多个金融市场之间风险相互传染的特征。何青等(2018)结合系统性风险各类测度指标和宏观经济变量等，通过主成分分析分位数回归法，全面反映了在实体经济运行情况下的系统性金融风险指数。

以DCC-GARCH 为代表的GARCH 类模型关注了风险波动的集聚效应，王琳、沈沛龙(2017)通过DCC-GACH 模型，描述了我国上市银行之间的动态相关关系。严伟祥等(2017)使用DCC-CoVaR 模型，分析了银行业、证券业、保险业、信托业的系统性风险。Xu et al.(2018)通过DCC-MIDAS-t 模型来估计CoVaR 模型，以此来研究中国银行机构的系统性风险。

Copula 模型常用于描述金融机构和金融市场之间非线性和时变性的风险相关关系，Juan and Andrea(2015)使用时变Copula-CoVaR 模型，分别度量了希腊债务危机爆发前后对欧洲主权债务市场的系统性风险。Li et al.(2018)将VMD 方法引入到时变Copula-CoVaR 模型之中，以此全面反映石油市场和股票市场系统性风险的短期效应和长期效应。周孝华和陈九生(2016)结合极值理论，构建了Copula-ASV-EVT-CoVaR 模型，比较了我国中小板与创业板市场之间的风险溢出效应。Shahzad et al.(2018)通过藤Copula-CoVaR 模型研究了各个主要股票市场的上下尾风险溢出效应和尾部相依风险。许启发等(2018)通过藤Copula-CAViaR 模型来估计多元条件联合分布，可以描述多个金融市场间的风险溢出效应。

国内外学者对系统性金融风险的研究对象较多地研究股票市场和债券市场，而较少涉及股票市场和公司债市场。公司债市场作为债券市场重要的组成部分，具有一定的研究价值，文章在国内外学者研究方法的基础上，对股票市场和公司债市场的相依性和风险传染效应进行系统分析，具体的结构安排如下：首先，模型介绍，包括以GPD-Copula 模型为基础的相依性和以Copula-CoVaR 模型为基础的风险溢出效应；其次，基于股票市场和公司债市场的日收益率序列数据，对股票市场和公司债市场的相依性和风险溢出效应结果进行分析和说明；最后，总结全文，并提出相关的风险防控建议。

二、模型构建

1. GPD 模型

在构建股票市场和公司债市场的相依性和风险溢出效应的度量模型之前，需要选择和确定一个拟合效果较好的边缘分布，分别对股票市场和公司债市场的收益率序列进行拟合。大量金融事实和历史数据表明，金融时间序列具有“波动集聚、厚尾、非线性相关”的特性，一般的正态分布由于忽略了极端金融事件，不能准确刻画其收益率序列的损失分布，而GPD 模型弥补了这个缺陷，对尾部特征能够进行有效描述。

GPD 模型只针对超过阈值u 的金融时间序列数据构建模型，其分布的定义表示为：

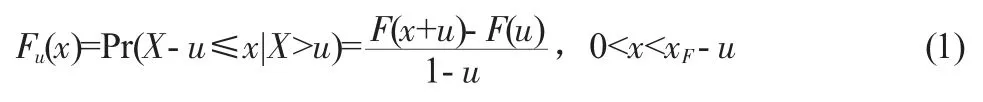
其中，xF为分布F 的右端点。当u 充分大时，分布函数Fu(x)会收敛于 GPD 分布 （Generalized Pareto Distribution） Gξ，σ(x)。

GPD 模型属于极值分布，常适用于刻画金融时间序列的尾部分布。具体定义如下：

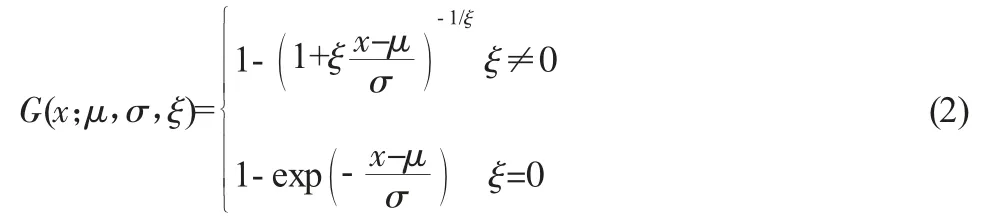
其中，μ为位置参数，σ为尺度参数，ξ为形状参数。

2. Copula 模型

金融时间序列往往是厚尾和非线性的，一般的计量模型难以满足经典假设条件。相比于格兰杰因果检验和Pearson 线性相关系数，Copula 模型主要用于描述金融时间序列之间非线性、非对称性和时变性的风险相关关系，特别是极端事件下的尾部依赖性，故本文选择Copula 模型来研究金融时间序列之间的风险相依性。根据Sklar(1959)的定义，Copula 有如下性质：

假设F1(x)和F2(y)是连续的一元分布函数，令u=F1(x)，ν=F2(y)，即C(u，ν)为边缘分布服从[0，1]均匀分布的二元分布函数。令F(x，y)为边缘分布函数F1(x)和F2(y)的联合分布函数，则有且仅有一个Copula 函数C 满足如下关系：

由以上等式可知，Copula 函数为连接联合分布函数和其边际分布的函数，故Copula 函数又称为连接函数。Copula 模型的关键是如何拟合边际分布和确定最优Copula 函数，具体而言，文章首先使用GPD 模型来拟合股票市场和公司债市场收益率序列的边际分布；然后使用IFM的估计方法进行参数估计，根据AIC 和 BIC 准则确定最优 Copula 函数；最后计算 Kendall τ 相关系数、Spearman ρ 相关系数和上下尾相关系数。

文章选择常用的Gaussian Copula、t Copula、Gumbel Copula、Frank Coplua、 Clayton Copula、 BB3 Copula 和 BB7 Copula 等Copula 函数进行拟合效果对比分析。各类Copula 的基本特点不尽相同，其中，Gaussian Copula 函数为对称且不存在尾部相关关系，t Copula 函数具有对称的尾部相关特征，Gumbel Copula函数具有较强的上尾相关和较弱的下尾相关，Frank Coplua 函数具有对称的弱尾相关，Clayton Copula 函数具有较强的下尾相关和较弱的上尾相关。值得注意的是，BB3 Copula 和BB7 Copula等类含有双参数，能够同时估计上尾和下尾的相关关系。

对于Copula 模型的参数估计，由于各类Copula 函数的未知参数较多，普通的极大似然估计方法不能有效解决参数的满足条件较为严格和计算时间较长等问题，基于此文章采用IFM（推断函数法） 的估计方法。具体参数估计步骤主要包括：第一步是估计股票市场和公司债市场边缘分布的参数，第二步是在既定的边缘分布参数基础上，再估计Copula 函数的各个参数。

对于Copula 模型的风险相依性测度，文章主要使用金融风险相依性中较为常用的 Kendall τ 相关系数、Spearman ρ 相关系数和上下尾相关系数。其中，Kendall τ 相关系数和Spearman ρ相关系数均属于秩相依性范畴，不需要边际分布，仅考虑随机变量之间的联合分布；尾部相关系数分为上尾相关系数λup和下尾相关系数λlow，主要用以度量尾部极端的相依性，包括上尾相关、下尾相关和上下尾对称三种相依情况。各个相关关系的基本定义如下：

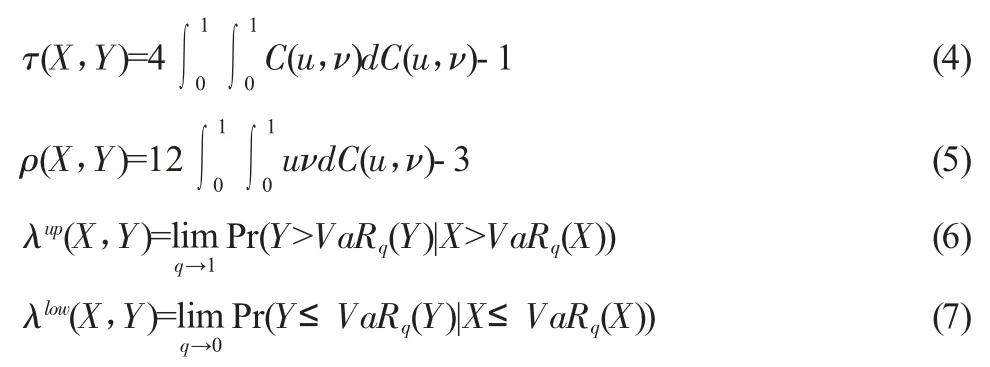
其中，τ 为 Kendall τ 相关系数，ρ 为 Spearman ρ 相关系数、λup和λlow分别为上尾相关关系和下尾相关系数。

3. CoVaR 模型

文章以股票市场对公司债市场的风险溢出效应为例进行模型说明。根据Adrian and Brunnermeier(2016)，对CoVaR 模型的定义如下：

其中，i 代表股票市场，j 代表公司债市场，q 代表分位数点。CoVaR 表示在股票市场发生危机的条件下，公司债市场面临的条件风险值。

相对于DCC-GARCH 和分位数回归等其他估计方法，Copula 模型能够较为全面地反映金融风险的非线性、厚尾性和非对称性等特征，故文章使用Copula 模型来估计CoVaR 模型。具体的估计过程如下：

假设股票市场收益率序列Xi和公司债市场收益率序列Xj的联合分布密度函数及其边缘分布密度函数分别为f(xi，xj)，fi(xi)，fj(xj)的条件分布密度函数为：

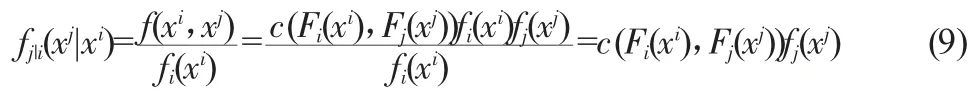
其中，Fi(xi)和Fj(xj)分别代表股票市场和公司债市场的边缘分布，即Fi(xi)和 Fj(xj)分别为fi(xi)和 fj(xj)的导数，c 为最优Copula 函数的密度函数。对式(9)进行积分变换，具体形式如下：

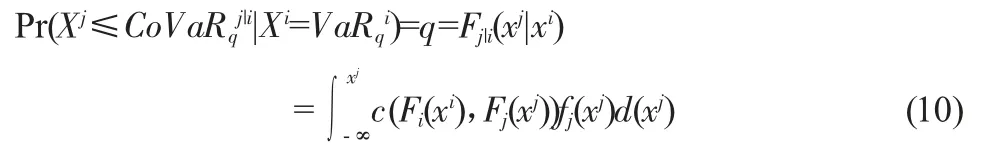
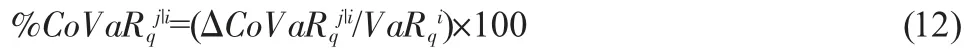
三、实证结果与分析

1. 数据来源与描述分析

文章主要研究股票市场和公司债市场的相依性和风险溢出效应。文章选择沪深300 指数（指数代码：399300.SZ） 代表股票市场，包括了上海和深圳证券市场的代表性股票，能够从整体上反映股票市场中的价格变化特征。同时，文章选择中证公司债指数（指数代码：399923.SZ） 代表公司债市场，包括了在上海和深圳证券交易所上市的公司债券。具体而言，文章以沪深300 指数和中证公司债指数的日收盘价为基础数据，分别得到股票市场和公司债市场的收益率序列，并以此为基础进行实证分析。文章以交易时间较晚的中证公司债指数为基准时间，数据来源于Wind 数据库，时间范围为2008 年1 月2 日至2019年6 月 30 日，统计量为2794 个，主要使用S-Plus 软件和Matlab 软件进行数据分析。

表1 为股票市场和公司债市场收益率序列数据的描述性统计结果，根据偏度和峰度可知，股票市场和公司债市场的偏度和峰度均远离0 和3；同时，JB 统计量的P 值为0，拒绝原假设。因此，股票市场和公司债市场收益率序列均不服从正态分布，具有尖峰厚尾特性。为了更进一步地反映股票市场和公司债市场收益率序列的非正态性和尾部特征，文章分别做出股票市场和公司债市场收益率序列的QQ 图。

表1 描述性统计量

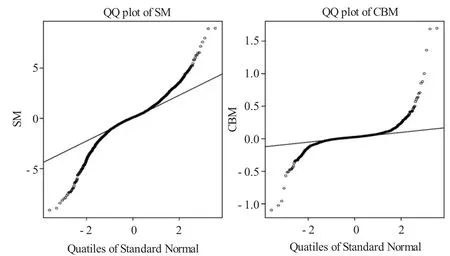
图1 股票市场和公司债市场收益率序列的QQ 图

图1 从左至右分别为股票市场和公司债市场收益率序列的QQ 图，股票市场和公司债市场收益率序列的上尾和下尾均偏离正态分布，表明股票市场和公司债市场均存在极端损失的现象，具有显著的厚尾特征，正态分布不能有效地拟合和刻画股票市场和公司债市场的边际损失分布，而极值分布能够侧重反映股票市场和公司债市场的尾部。

2. 边际分布的确定和拟合

为了更为准确地刻画股票市场和公司债市场收益率序列的损失分布，文章使用GPD 分布来拟合收益率序列的尾部特征。另外，对于GPD 分布阈值的选取，文章使用Du Mouchel 10%原则来分别确定股票市场和公司债市场收益率序列的上尾阈值和下尾阈值，该方法简单实用，能够较为准确地确定GPD 分布的阈值和拟合分布。

文章使用MLE 的估计方法对GPD 分布的三个参数进行估计。在表2 中，μ 代表GPD 分布的上尾和下尾阈值，Pμ代表超出阈值的样本数据比例，ξ 代表形状参数估计值，σ 代表尺度参数估计值。根据表2 可知，在超出样本数据占全部收益率序列数据的9.99%基础上，股票市场的上尾阈值为1.9162，大于公司债市场的上尾阈值 0.0909，而股票市场收益率序列的均值小于公司债市场收益率序列。另外，在超出样本数据占全部收益率序列数据的9.96%基础上，股票市场的下尾阈值为-1.8863，小于公司债市场的下尾阈值-0.0398，这与上尾的特征情况正好相反。

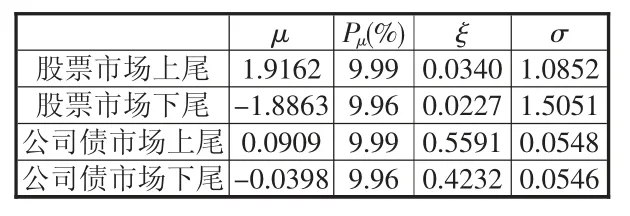
表2 股票市场和公司债市场收益率序列的上尾和下尾参数估计

在参数估计之后，文章对GPD 分布的拟合效果进行检验，GPD 分布的检验方法主要包括超出分布、尾部分布、残差散点图和残差QQ 图等。超出分布是GPD 分布的最主要检验方法，GPD 分布也是对超出阈值的部分数据进行拟合，故文章主要使用超出分布进行GPD 分布的检验。限于篇幅，文章不对其他的检验方法进行拟合效果检验。

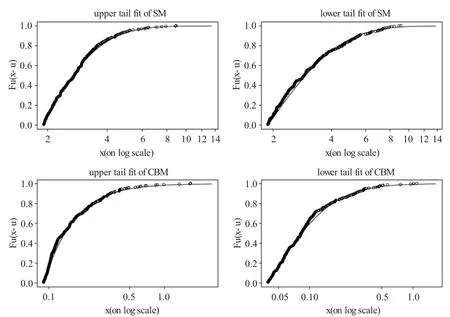
图2 股票市场和公司债市场收益率序列GPD 分布的上尾和下尾拟合诊断图

在图2 中，从左至右、从上至下分别表示股票市场的上尾和下尾、公司债市场的上尾和下尾拟合情况。根据图2 可知，股票市场(SM)和公司债市场(CBM)的上尾和下尾绝大部分的点均在超出分布拟合的曲线上，表明股票市场和公司债市场的上下尾阈值选取较好，GPD 分布能够显著地拟合股票市场和公司债市场收益率序列的边际损失分布，在刻画其尾部分布方面的效果较好。

3. 股票市场和公司债市场的相依结构

在确定股票市场和公司债市场的边际分布之后，文章使用Copula 模型来研究股票市场和公司债市场的相依性强度。具体而言，首先，通过AIC 和BIC 等原则确定最优Copula；其次，基于最优Copula 函数及其参数估计结果，分别计算各个相关系数。

对于Copula 函数的选择，文章主要使用Gaussian Copula、Gumbel Copula、Galambos Copula、Frank Copula、Clayton Copula和BB7 Copula 等6 种常用Copula 函数，这些Copula 函数包含了上下尾、对称性和非线性等重要金融特征。根据表3 可知，Galambos Copula的loglike 值最大，且 AIC 和 BIC 最小。其次拟合效果较好的是Gaussian Copula， 拟合效果最差的是Frank Copula。因此，股票市场和公司债市场收益率序列连接的最优Copula 函数为Galambos Copula。

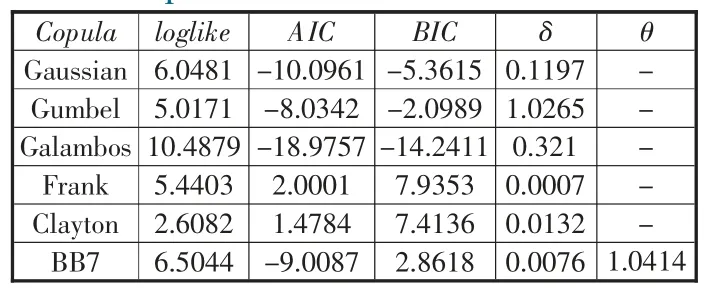
表3 Copula 模型的参数估计和检验结果

图3 和图4 分别为参数 δ 为 0.3210 的 Galambos Copula 的概率密度图和累积分布图。根据图3 和图4可知，Galambos Copula函数具有上尾相关的非对称特性，即股票市场和公司债市场的上尾相依性大于下尾相依性。

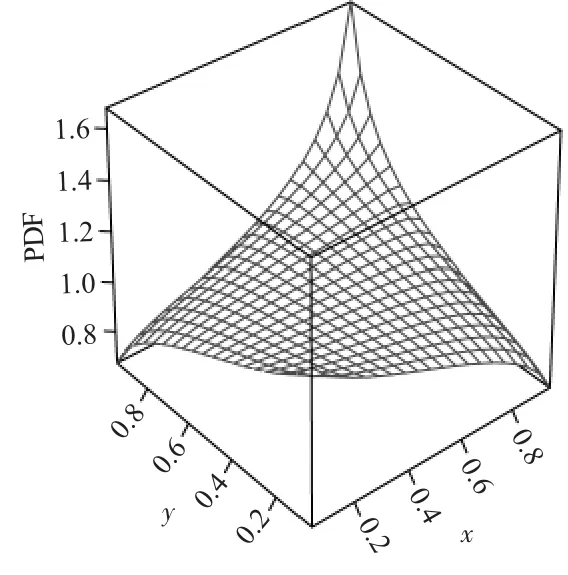
图3 概率密度图

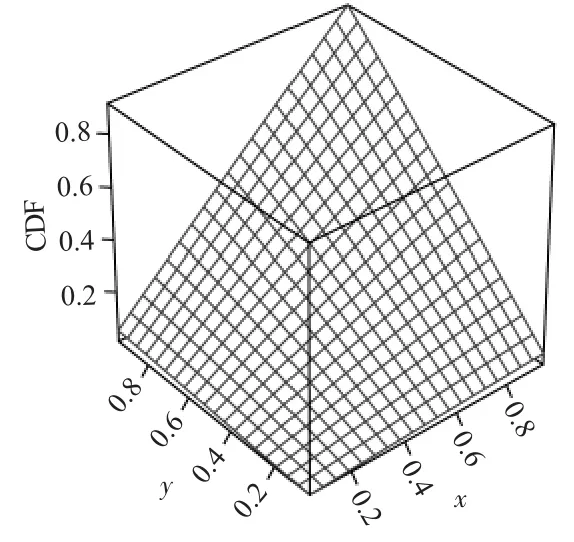
图4 累积分布图

基于Galambos Copula 和其参数估计结果，可以计算出股票市场和公司债市场之间的风险相依性系数。根据表4 可知，股票市场和公司债市场之间存在正向的相依性，但相依程度较小，表明股票市场和公司债市场的关联紧密程度较弱，投资者同时投资股票和公司债的规模和比重较小。另外，股票市场和公司债市场存在上尾相关关系，尾部相依较为显著。当某个市场释放有利消息时，其价格处于上涨期，导致另外一个市场的价格也随之显著上涨。因此，股票市场和公司债市场对牛市较为敏感，容易受到经济发展状况良好、积极宽松的财政货币政策和利好消息等正面环境的影响，而对相关的负面状况和展望影响较小。

表4 股票市场和公司债市场的相依结构

4. 股票市场和公司债市场的风险溢出效应

文章的分位数设置为5%，根据前文Copula 的估计结果以及CoVaR 的计算步骤，可以得到股票市场和公司债市场的风险价值、条件风险价值和风险溢出效应，具体结果如表5 所示。

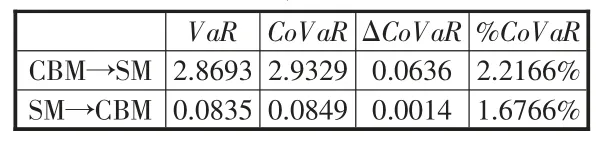
表5 股票市场和公司债市场间的风险溢出效应统计量

根据表5 可知，股票市场的 VaR 值为 2.8693，而公司债市场的VaR 值为0.0835，说明股票市场的风险大于公司债市场的风险。同时，根据ΔCoVaR和%CoVaR可知，股票市场对公司债市场的风险溢出效应分别为0.0636 和2.2166%，大于公司债市场对股票市场的风险溢出效应，股票市场和公司债市场之间存在非对称的双向风险溢出效应。当股票市场发生较大的价格波动和危机时，由于其规模大和流动性强等特点，金融其他市场更容易形成恐慌，投资者的追涨涨杀跌行为通过正反馈机制导致恶性循环，致使其杠杆率激增，同时投资者的风险偏好往往受到外在的影响，即所谓的“羊群效应”，最终导致股票市场对公司债市场的联动风险，系统性金融风险的增加和爆发。

四、结论

文章通过GPD 分布来分别拟合股票市场和公司债市场的边际分布，通过AIC 原则和BIC 原则确定最优Copula 为Galambos Copula 函数，并据此计算出股票市场和公司债市场的风险相依性系数，最后通过Copula 模型估计股票市场和公司债市场的风险溢出效应。结果表明，第一，对于风险相依性而言，股票市场和公司债市场的相依性程度较低，但存在上尾相关关系，这需要相关投资者和金融风险监管部门的注意；第二，对于风险程度而言，相比于公司债市场，股票市场在风险价值和风险溢出效应方面均较大，表明股票市场的风险将是重点的监管对象，同时也要注意和兼顾“太关联而不能倒”的公司债市场。同时，文章由于侧重金融时间序列的厚尾性，重点探讨了股票市场和公司债市场风险溢出效应的规模问题，仅构建静态的GPD-Copula-CoVaR 模型，但忽略了金融风险的时变性特征，今后将构建时变Copula-CoVaR 模型来研究金融市场的动态风险溢出效应。

对于股票市场和公司债市场中的金融风险和风险传染影响，需要建立和完善风险研判机制、决策风险评估机制、风险防控协调机制和风险防控责任机制等风险防控机制。第一，从风险机制层面看，以往的金额风险监管忽略了事前防范，风险防范能够有效地减少风险损失和预防危机的发生。具体而言，需要健全和完善股票市场和公司债市场的风险预警机制，构建包括金融市场、宏观经济和国际冲击等层面的股票市场和公司债市场间系统性金融风险预警指标体系，对股票市场和公司债市场间的风险溢出效应进行科学的预测和评估，提升系统性金融风险的防范能力和效果。第二，从政府监管层面看，加强金融监管机构之间的协调和配合，以应付复杂和关联的跨行业和跨市场的风险传染；完善股票市场和公司债市场的应急管理和处置方案，以应付极端的系统性金融风险；强化和细化风险防控责任机制，以明确股票市场和公司债市场的风险监管责任人；健全股票市场和公司债市场的风险监管细则，以提供相关的法律监管依据；关注世界主要股票市场和以公司债市场为代表的债券市场对我国主要金融市场的风险传染和冲击，加强国际监管和合作；关注金融和经济以外的金融风险传染因素，如政治、政策和文化等，提高监管格局。第三，从政府政策层面看，执行“货币政策+宏观审慎管理”双支柱政策框架，权衡好货币政策和风险监管之间的关系，在确保合理控制股票市场和公司债市场系统性金融风险的前提下，通过稳健的货币政策，并配合积极的财政政策，以适应危机救助和经济新常态下的经济大环境，刺激金融市场和宏观经济的繁荣发展，解决企业融资难和投资者最优投资的问题，使股票市场和公司债市场更好地服务于实体经济。